1
大学数学基礎解説
文献あり

ペアノ算術で加法交換法則の証明図をかく

証明図,ペアノ算術,自然数
934
0
$$\newcommand{B}[1]{\left[ #1 \right]} \newcommand{CA}[1]{(\text{CA}#1)} \newcommand{CAA}[0]{(\text{反射律})} \newcommand{CAB}[0]{(\text{対称律})} \newcommand{CAC}[0]{(\text{推移律})} \newcommand{CAD}[0]{(\text{代入律(関数)})} \newcommand{CAE}[0]{(\text{代入律(述語)})} \newcommand{hvec}[1]{\begin{eqnarray} \left. \begin{array}{c} #1 \end{array} \right. \end{eqnarray}} \newcommand{MI}[0]{(\text{数学的帰納法})} \newcommand{p}[1]{\left( #1 \right)} \newcommand{PAA}[0]{(\text{PA1})\; \forall n. \lnot(sn=0)} \newcommand{PAB}[0]{(\text{PA2})\;\forall m. \forall n. (sm=sn\to m=n)} \newcommand{PAC}[0]{(\text{PA3})\; \forall n. (n+0=n)} \newcommand{PAD}[0]{(\text{PA}4)\; \forall m. \forall n. (m+sn=s(m+n))} \newcommand{To}[0]{\vdash} $$

本記事では，ペアノ算術の加法交換法則の証明図をかいていきたいと思います．

ペアノ算術の各種法則の証明は，等式変形をやっていけばそれほど難しいものではないですが，$\forall$の付け外しなど，色々とすっ飛ばして書くことになります．
せっかく基礎まで立ち返って証明をやっているのにそれではもったいないので，1段階ずつ推論規則を追って加法交換法則を証明し，証明図にしていこうと思います．

なお，本記事は参考文献にあげた資料および筆者が数年前に受けた記号論理学の講義の記憶をもとに構成されています．
独自の定義を含む可能性がありますので，レポートなどのためにこの記事を見つけられた方はご注意ください．

定義

証明の前にまず必要事項の定義をまとめていきます．

記号

まずは記号の定義です．
ここを厳密に構成するのは筆者の手に余るので自然言語的な説明でお許しください．

記号
  • $X, Y, Z,\dots$：命題変数
    真または偽の値を取る変数
  • $P, Q, R, \dots$：述語変数
    1つ以上の変数を取って命題となる．
  • $\land, \lor, \to, \lnot, \forall, \exists$：論理記号
    $\land, \lor, \to$は2つ，$\lnot$は1つの命題を引数にとり，命題を返す演算子．
    $\forall, \exists$は$\forall x.P(x)$のかたちで束縛変数を含む命題を作る演算子．
  • $a, b, c, \dots$： (自由)変数
    述語の引数となる記号．
  • $x, y, z, \dots$： 束縛変数
    $\forall, \exists$によって束縛され証明の外部には出てこない変数．
  • $f, g, \dots$：関数
    1つ以上の変数を取って変数となる．

推論規則

古典一階述語論理の推論規則です．
本項は文献[1-4]を元に，(ちょいちょい表記がブレるので)筆者が構成したものです．

～$I$・～$E$はそれぞれ～の導入則・除去則を表します．
「$P\vdash Q$」は $P$ から $Q$ が証明されることを意味するメタ記号で，$\Rightarrow$と同じような意味です．ただし，論理記号の$\to$とは区別します．

推論規則
  • $\land I$： $X,Y\vdash X\land Y$
  • $\land E$： $X\land Y\vdash X,\quad X\land Y\vdash Y$
  • $\lor I$： $X\vdash X\lor Y,\quad Y\vdash X\lor Y$
  • $\lor E$： $X\lor Y, [X]\cdots Z,[Y]\cdots Z \vdash Z $
  • $\lnot I$： $[X]\cdots \bot \vdash \lnot X$
  • （$\lnot E$： $X,\; \lnot X\vdash \bot$）
  • $\to I$： $[X]\cdots Y\vdash X\to Y$
  • $\to E$： $X\to Y,\; X\vdash Y$
  • $\forall I$： $P(x) \vdash \forall x. P(x)$
  • $\forall E$： $\forall x.P(x)\vdash P(a)$
  • $\exists I$： $P(a) \vdash \exists x.P(x)$
  • $\exists E$： $\exists x.P(x),\;[P(a)]\cdots Q\vdash Q$

$[\phantom{X}]$は推論の際に仮定から外れるという意味で，証明図では
$$ \dfrac{\hvec{&[X]^{(n)} & [Y]^{(n)}\\& \vdots^{\phantom{(n)}} & \vdots^{\phantom{(n)}}\\X\lor Y & Z^{\phantom{(n)}} & Z^{\phantom{(n)}}}}{Z}{\lor E}^{(n)} $$
のようにどこの推論に対応する仮定なのかわかるようマークをつけたりします．

排中律（$\lnot E$）を含まなければ直観主義論理です．今回の証明では多分使っていないので直観主義論理の範囲でも証明可能ということですね．

等号

「数」を扱うのに必要な等号「$=$」を導入します．
ここで，公理として「$\to$」が入った命題があると式変形がとてつもなくめんどくさくなるので，文献[5]の「相等公理CA」をもとに推論規則を追加する形で定義します．

変数$x,y$を取って命題$x=y$となる2項演算子$=$を以下のように定めます．

$=$の推論
  1. 反射律： $\vdash x=x$
  2. 対称律： $x=y \vdash y=x$
  3. 推移律： $x=y,\ y=z \vdash x=z$
  4. 代入律1： 任意の関数$f$について $x=y \vdash f(\dots,x,\dots)=f(\dots,y,\dots)$
  5. 代入律2： 任意の述語$P$について $x=y, P(\dots,x,\dots) \vdash P(\dots,y,\dots)$

ペアノ算術

「自然数」における演算を以下の公理系で定義します．(参考：[4,6])

ペアノ算術

記号

  • $0$：定数記号
  • $s$：1変数関数
  • $+, \times$： 2変数関数

公理系（PA）

  1. (PA1)： $\forall n. \lnot(sn = 0)$
  2. (PA2)： $\forall m. \forall n. (sm=sn\to m=n)$
  3. (PA3)： $\forall n. (n+0=n)$
  4. (PA4)： $\forall m. \forall n. (m+sn=s(m+n))$
  5. (PA5)： $\forall n. (n\times 0=0)$
  6. (PA6)： $\forall m. \forall n. (m\times sn=(m\times n)+n)$
  7. 数学的帰納法： 任意の述語$P(\dots,n,\dots)$について，$P(\dots,0,\dots),\; \forall n. (P(\dots,n,\dots)\to P(\dots,sn,\dots))\vdash \forall n. P(\dots,n,\dots)$

証明

ここまでに定義した推論規則・公理を使って

自然数の加法の交換法則

$$ \forall x. \forall y. (x+y=y+x) $$

を証明します．
全称量化が2つあるので，2重の数学的帰納法で証明していきます．
適宜用いた推論規則や公理を()で付記します．

(I)
(I-i)
$$\To 0+0=0+0\quad \CAA \tag{1}$$

(I-ii)
$$\PAD \To \forall n. 0+sn = s(0+n)\quad (\forall E)$$
$$\quad\To 0+sk = s(0+k)\quad (\forall E) \tag{2}$$
$$\B{0+k=k+0}^A \To s(0+k)=s(k+0)\quad \CAD \tag{3}$$
$$\PAC \To k+0=k\quad (\forall E)$$
$$\quad\To s(k+0)=sk\quad \CAD \tag{4}$$
$$(2),(3)\To 0+sk=s(k+0)\quad \CAC \tag{5}$$
$$(5),(4)\To 0+sk=sk\quad \CAC \tag{6}$$
$$\PAC \To sk+0=sk\quad (\forall E)$$
$$\quad\To sk=sk+0\quad \CAB \tag{7}$$
$$(6),(7)\To 0+sk=sk+0\quad \CAC \tag{8}$$
$$[\phantom{x}]^A \cdots(8)\To(0+k=k+0\to 0+sk=sk+0)\quad(\to I)$$
$$\quad \To \forall k.(0+k=k+0\to 0+sk=sk+0)\quad(\forall I) \tag{9}$$

$$(1),(9)\To \forall y. (0+y=y+0)\quad\MI\tag{10}$$

(II)
$$\PAD \To sl+sn=s(sl+n) \quad (\forall E)$$
$$\quad\To sl+sk=s(sl+k) \quad (\forall E)\tag{11}$$
$$[sl+k=k+sl]^B \To s(sl+k)=s(k+sl)\quad\CAD\tag{12}$$
$$(11),(12)\To sl+sk=s(k+sl)\quad\CAC\tag{13}$$
$$\PAD \To \forall n. k+sn=s(k+n) \quad (\forall E)$$
$$\quad \To k+sl=s(k+l) \quad (\forall E)$$
$$\quad \To s(k+sl)=ss(k+l) \quad\CAD\tag{14}$$
$$(13),(14)\To sl+sk=ss(k+l) \quad\CAC\tag{15}$$

$$\PAD \To \forall n. sk+sn=s(sk+n) \quad (\forall E)$$
$$\quad\To sk+sl=s(sk+l) \quad (\forall E)\tag{16}$$
$$[\forall y. l+y=y+l]^C\To l+sk=sk+l\quad(\forall E)$$
$$\quad\To sk+l=l+sk\quad\CAB$$
$$\quad\To s(sk+l)=s(l+sk)\quad\CAD\tag{17}$$
$$(16),(17)\To sk+sl=s(l+sk)\quad\CAC\tag{18}$$
$$\PAD \To \forall n. l+sn=s(l+n) \quad (\forall E)$$
$$\quad\To l+sk=s(l+k) \quad (\forall E)$$
$$\quad\To s(l+sk)=ss(l+k)\quad\CAD\tag{19}$$
$$(18),(19)\To sk+sl=ss(l+k)\quad\CAC\tag{20}$$
$$[\forall y. l+y=y+l]^C\To l+k=k+l\quad(\forall E)$$
$$\quad\To ss(l+k)=ss(k+l)\quad\CAD\tag{21}$$
$$(20),(21)\To sk+sl=ss(k+l) \quad\CAC$$
$$\quad\To ss(k+l)=sk+sl\quad\CAB\tag{22}$$
$$(15),(22)\To sl+sk=sk+sl\quad\CAC\tag{23}$$
$$[\phantom{x}]^B\cdots(23)\To(sl+k=k+sl)\to(sl+sk=sk+sl)\quad(\to I)$$
$$\quad\To \forall k. (sl+k=k+sl)\to(sl+sk=sk+sl) \quad(\forall I)\tag{24}$$

$$(10)\To 0+sl=sl+0\quad(\forall E)$$
$$\quad\To sl+0=0+sl\quad\CAB\tag{25}$$
$$(25),(24)\To \forall y. sl+y=y+sl \quad\MI\tag{26}$$
$$[\phantom{x}]^C,[\phantom{x}]^C\cdots(26)\To(\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)\quad(\to I)$$
$$\quad\To \forall l. (\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)\quad(\forall I)\tag{27}$$

$$(10),(27)\To\forall x. \forall y.x+y=y+x \quad\MI\tag{Q.E.D.}$$

この証明を証明図にするとこのようになります．

証明図-全体 証明図-全体

いくらなんでも見づらすぎるので前半部分を分割すると，以下のようになります．

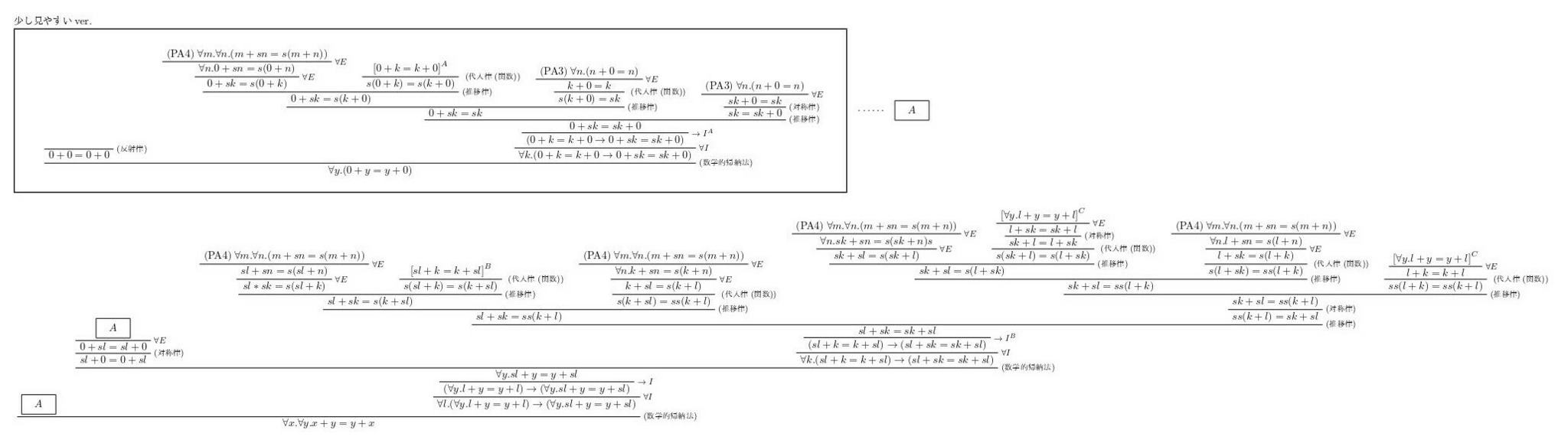証明図-分割 証明図-分割

bussproofs パッケージを用いてLaTeXで描画しています．
すぐ紙幅をはみ出すので調整が大変です．

以上です．
今後，機会があれば他の法則の証明もやってみようと思います．
間違いなどありましたらコメントで教えていただけると幸いです．

Appendix-LaTeXソースコード

面倒がってマクロを濫用した汚いコードですが，参考に置いておきます．
※マークダウン記法と干渉しておかしな表示になってるのでソースコードを参照してください．

      \documentclass[a4paper,8pt]{jsarticle}
\usepackage{graphicx}
\usepackage{amssymb}
\usepackage{bussproofs}
%\usepackage{proof}
  
\newcommand{\CAA}{(反射律)}
\newcommand{\CAB}{(対称律)}
\newcommand{\CAC}{(推移律)}
\newcommand{\CAD}{ (代入律(関数))}
\newcommand{\CAE}{(代入律(述語))}

\newcommand{\PAA}{$(\mathrm{PA1})\; \forall n. \lnot(sn=0)$}
\newcommand{\PAB}{$(\mathrm{PA2})\;\forall m. \forall n. (sm=sn\to m=n)$}
\newcommand{\PAC}{$(\mathrm{PA3})\; \forall n. (n+0=n)$}
\newcommand{\PAD}{$(\mathrm{PA}4)\; \forall m. \forall n. (m+sn=s(m+n))$}
\newcommand{\MI}{(数学的帰納法)}

\let\A\AxiomC
%\let\R\RightLabel
\newcommand{\R}[1]{\RightLabel{{\footnotesize #1}}}
\let\U\UnaryInfC
\let\B\BinaryInfC
\let\T\TrinaryInfC

\newcommand{\paren}[1]{\left( #1 \right)}
\newcommand{\bracket}[1]{\left[ #1 \right]}
\newcommand{\To}{\vdash}

\begin{document}
\rotatebox{270}{
\scalebox{0.3}{
\parbox{2.7\linewidth}{
\begin{prooftree}
%
\A{}
\R{\CAA}
\U{$0+0=0+0$}%(1)
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. 0+sn=s(0+n)$}
\R{$\forall E$}
\U{$0+sk = s(0+k)$}%(2)
%
\A{$\bracket{0+k=k+0}^A$}
\R{\CAD}
\U{$s(0+k)=s(k+0)$}%(3)
\R{\CAC}
\B{$0+sk=s(k+0)$}%(5)
%
\A{\PAC}
\R{$\forall E$}
\U{$k+0=k$}
\R{\CAD}
\U{$s(k+0)=sk$}%(4)
\R{\CAC}
\B{$0+sk=sk$}%(6)
%
\A{\PAC}
\R{$\forall E$}
\U{$sk+0=sk$}
\R{\CAB}
\U{$sk=sk+0$}%(7)
\R{\CAC}
\B{$0+sk=sk+0$}%(8)
\R{$\to I^A$}
\U{$(0+k=k+0\to 0+sk=sk+0)$}
\R{$\forall I$}
\U{$\forall k.(0+k=k+0\to 0+sk=sk+0)$}%(9)
\R{\MI}
\B{$\forall y. (0+y=y+0)$}
%
\A{}
\R{\CAA}
\U{$0+0=0+0$}%(1)
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. 0+sn=s(0+n)$}
\R{$\forall E$}
\U{$0+sk = s(0+k)$}%(2)
%
\A{$\bracket{0+k=k+0}^A$}
\R{\CAD}
\U{$s(0+k)=s(k+0)$}%(3)
\R{\CAC}
\B{$0+sk=s(k+0)$}%(5)
%
\A{\PAC}
\R{$\forall E$}
\U{$k+0=k$}
\R{\CAD}
\U{$s(k+0)=sk$}%(4)
\R{\CAC}
\B{$0+sk=sk$}%(6)
%
\A{\PAC}
\R{$\forall E$}
\U{$sk+0=sk$}
\R{\CAB}
\U{$sk=sk+0$}%(7)
\R{\CAC}
\B{$0+sk=sk+0$}%(8)
\R{$\to I^A$}
\U{$(0+k=k+0\to 0+sk=sk+0)$}
\R{$\forall I$}
\U{$\forall k.(0+k=k+0\to 0+sk=sk+0)$}%(9)
\R{\MI}
\B{$\forall y. (0+y=y+0)$}
\R{$\forall E$}
\U{$0+sl=sl+0$}
\R{\CAB}
\U{$sl+0=0+sl$}%(25
%
\A{\PAD}
\R{$\forall E$}
\U{$sl+sn=s(sl+n)$}
\R{$\forall E$}
\U{$sl*sk=s(sl+k)$}%(11)
%
\A{$\bracket{sl+k=k+sl}^B$}
\R{\CAD}
\U{$s(sl+k)=s(k+sl)$}%(12)
\R{\CAC}
\B{$sl+sk=s(k+sl)$}%(13)
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. k+sn=s(k+n)$}
\R{$\forall E$}
\U{$k+sl=s(k+l)$}
\R{\CAD}
\U{$s(k+sl)=ss(k+l)$}%(14)
\R{\CAC}
\B{$sl+sk=ss(k+l)$}%(15
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. sk+sn=s(sk+n)s$}
\R{$\forall E$}
\U{$sk+sl=s(sk+l)$}%(16
%
\A{$\bracket{\forall y. l+y=y+l}^C$}
\R{$\forall E$}
\U{$l+sk=sk+l$}
\R{\CAB}
\U{$sk+l=l+sk$}
\R{\CAD}
\U{$s(sk+l)=s(l+sk)$}%(17
\R{\CAC}
\B{$sk+sl=s(l+sk)$}%(18
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. l+sn=s(l+n)$}
\R{$\forall E$}
\U{$l+sk=s(l+k)$}
\R{\CAD}
\U{$s(l+sk)=ss(l+k)$}%(19
\R{\CAC}
\B{$sk+sl=ss(l+k)$}%(20
%
\A{$\bracket{\forall y. l+y=y+l}^C$}
\R{$\forall E$}
\U{$l+k=k+l$}
\R{\CAD}
\U{$ss(l+k)=ss(k+l)$}%(21
\R{\CAC}
\B{$sk+sl=ss(k+l)$}
\R{\CAB}
\U{$ss(k+l)=sk+sl$}%(22
\R{\CAC}
\B{$sl+sk=sk+sl$}%(23
\R{$\to I^B$}
\U{$(sl+k=k+sl)\to(sl+sk=sk+sl)$}
\R{$\forall I$}
\U{$\forall k. (sl+k=k+sl)\to(sl+sk=sk+sl)$}%(24
\R{\MI}
\B{$\forall y. sl+y = y+sl$}%(25
\R{$\to I$}
\U{$(\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)$}
\R{$\forall I$}
\U{$\forall l. (\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)$}%(27
\R{\MI}
\B{$\forall x. \forall y.x+y=y+x$}
\end{prooftree}}}}
\newpage

\scalebox{0.4}{少し見やすいver.}

\fbox{
\scalebox{0.4}{
\parbox{1.4\linewidth}{
\begin{prooftree}
\A{}
\R{\CAA}
\U{$0+0=0+0$}%(1)
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. 0+sn=s(0+n)$}
\R{$\forall E$}
\U{$0+sk = s(0+k)$}%(2)
%
\A{$\bracket{0+k=k+0}^A$}
\R{\CAD}
\U{$s(0+k)=s(k+0)$}%(3)
\R{\CAC}
\B{$0+sk=s(k+0)$}%(5)
%
\A{\PAC}
\R{$\forall E$}
\U{$k+0=k$}
\R{\CAD}
\U{$s(k+0)=sk$}%(4)
\R{\CAC}
\B{$0+sk=sk$}%(6)
%
\A{\PAC}
\R{$\forall E$}
\U{$sk+0=sk$}
\R{\CAB}
\U{$sk=sk+0$}%(7)
\R{\CAC}
\B{$0+sk=sk+0$}%(8)
\R{$\to I^A$}
\U{$(0+k=k+0\to 0+sk=sk+0)$}
\R{$\forall I$}
\U{$\forall k.(0+k=k+0\to 0+sk=sk+0)$}%(9)
\R{\MI}
\B{$\forall y. (0+y=y+0)$}
\end{prooftree}
}
}
}\scalebox{0.4}{$\quad\cdots\cdots\quad$\fbox{$\phantom{X}A\phantom{\frac{X}{Y}}$}}

\scalebox{0.4}{
\parbox{2.7\linewidth}{
\begin{prooftree}
%
\A{\fbox{$\phantom{X}A\phantom{\frac{X}{Y}}$}}
%
\A{\fbox{$\phantom{X}A\phantom{\frac{X}{Y}}$}}
\R{$\forall E$}
\U{$0+sl=sl+0$}
\R{\CAB}
\U{$sl+0=0+sl$}%(25
%
\A{\PAD}
\R{$\forall E$}
\U{$sl+sn=s(sl+n)$}
\R{$\forall E$}
\U{$sl*sk=s(sl+k)$}%(11)
%
\A{$\bracket{sl+k=k+sl}^B$}
\R{\CAD}
\U{$s(sl+k)=s(k+sl)$}%(12)
\R{\CAC}
\B{$sl+sk=s(k+sl)$}%(13)
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. k+sn=s(k+n)$}
\R{$\forall E$}
\U{$k+sl=s(k+l)$}
\R{\CAD}
\U{$s(k+sl)=ss(k+l)$}%(14)
\R{\CAC}
\B{$sl+sk=ss(k+l)$}%(15
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. sk+sn=s(sk+n)s$}
\R{$\forall E$}
\U{$sk+sl=s(sk+l)$}%(16
%
\A{$\bracket{\forall y. l+y=y+l}^C$}
\R{$\forall E$}
\U{$l+sk=sk+l$}
\R{\CAB}
\U{$sk+l=l+sk$}
\R{\CAD}
\U{$s(sk+l)=s(l+sk)$}%(17
\R{\CAC}
\B{$sk+sl=s(l+sk)$}%(18
%
\A{\PAD}
\R{$\forall E$}
\U{$\forall n. l+sn=s(l+n)$}
\R{$\forall E$}
\U{$l+sk=s(l+k)$}
\R{\CAD}
\U{$s(l+sk)=ss(l+k)$}%(19
\R{\CAC}
\B{$sk+sl=ss(l+k)$}%(20
%
\A{$\bracket{\forall y. l+y=y+l}^C$}
\R{$\forall E$}
\U{$l+k=k+l$}
\R{\CAD}
\U{$ss(l+k)=ss(k+l)$}%(21
\R{\CAC}
\B{$sk+sl=ss(k+l)$}
\R{\CAB}
\U{$ss(k+l)=sk+sl$}%(22
\R{\CAC}
\B{$sl+sk=sk+sl$}%(23
\R{$\to I^B$}
\U{$(sl+k=k+sl)\to(sl+sk=sk+sl)$}
\R{$\forall I$}
\U{$\forall k. (sl+k=k+sl)\to(sl+sk=sk+sl)$}%(24
\R{\MI}
\B{$\forall y. sl+y = y+sl$}
\R{$\to I$}
\U{$(\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)$}
\R{$\forall I$}
\U{$\forall l. (\forall y.l+y=y+l)\to(\forall y. sl+y=y+sl)$}
\R{\MI}
\B{$\forall x. \forall y.x+y=y+x$}
\end{prooftree}
}}

\end{document}

参考文献

[1]
岩沼 宏治, 鍋島 英知, 井上 克巳, 一階論理上の等号推論：理論と実際, J-STAGE/コンピュータ ソフトウェア, 2011
[2]
Unknown, 取得中..., Mathlog, アクセス日: Sat Apr 22 2023
[3]
Ryo Takemura, 論理学入門, 閲覧日 2021年9月24日, https://abelard.flet.keio.ac.jp/person/takemura/class/2013/3-print-nk.pdf
[4]
照井 一成, 『数学』を数学的に考える, 平成21年度(第31回)数学入門公開講座テキスト(京都大学数理解析研究所，平成21年7月30日～8月2日開催), 閲覧日 2021年9月24日, https://www.kurims.kyoto-u.ac.jp/~kenkyubu/kokai-koza/terui.pdf
[5]
命題論理, 閲覧日 2021年9月24日, https://ja.wikipedia.org/wiki/%E5%91%BD%E9%A1%8C%E8%AB%96%E7%90%86
[6]
直観主義論理, 閲覧日 2021年9月24日, https://ja.wikipedia.org/wiki/%E7%9B%B4%E8%A6%B3%E4%B8%BB%E7%BE%A9%E8%AB%96%E7%90%86
投稿日：2021年9月26日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

❄雪下❄
❄雪下❄
1
934

コメント

他の人のコメント

コメントはありません。
読み込み中
❄雪下❄
❄雪下❄
ペアノ算術で加法交換法則の証明図をかく