日曜数学会発表資料「リーマン予想って結局何なの？」

はじめに

　この記事では私、子葉が10/23(土)に開催された第22回日曜数学会にて発表した内容をそれとなーくまとめたものになります(発表の一部始終については ここ で見れます)。全体的には私が前に書いた記事 リーマン予想って結局何が嬉しいの？ の内容を発表用に凝縮したものになってます。

リーマン予想から何がわかるのか

スライド1
　リーマン予想とは「ゼータ関数の非自明な零点が$\Re(s)=\frac12$に整列している」という話でしたが、もしそうだとして、何なの？という感じがします。実際「リーマン予想とはどういう主張であるか」は知っていても「リーマン予想から何がわかるのか」まで知っている人は少ないと思います。
　ただ、リーマンゼータ関数について勉強をしていると「ゼータ関数と素数は何か関係があるらしい」ということは耳にすると思います。実際リーマンが後にリーマン予想として知られるようになった一文を記した論文『与えられた数より小さな素数の個数について』にはゼータ関数と素数とを結びつける式：リーマンの素数公式というものが証明されています。というわけでこの$\pi(x)$を起点にリーマン予想から何がわかるのかを紐解いていきましょう。

スライド2
　$\pi(x)$とは$x$以下の素数の個数を表わす関数として定義されて、そのグラフ(青)はしばしば素数階段と呼ばれています。そしてこの素数階段は素数定理というものによって$x/\log x$(赤)とか対数積分$\mathrm{li}(x)$(緑)というグラフで近似できることが知られています。もっと言えば素数階段を重ねた関数$\Pi(x)$(橙)はその誤差のグラフ(赤)を見てもわかるようにほとんど$\mathrm{li}(x)$に一致していることがわかります。(この近似関係はゼータ関数が$\Re(s)=0,1$において零点を持たないことから導かれるのですが、)実はリーマン予想はこの誤差がどのくらいの大きさであるかまで教えてくれるのです。
(ちなみにこのグラフは ここ で見ることができます。)

スライド3
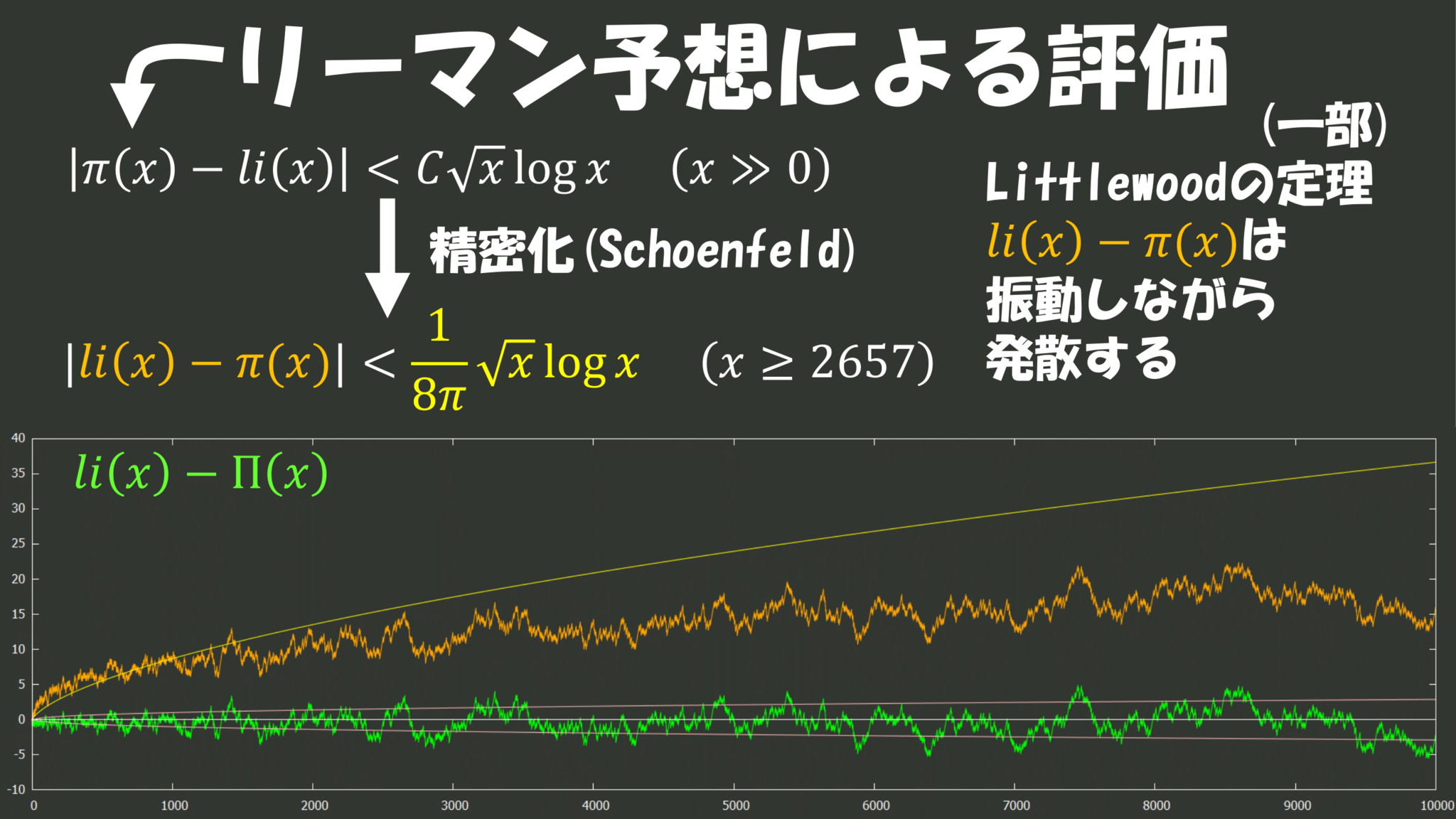
　具体的にはその誤差の大きさが高々$\sqrt x\log x$程度であるということがリーマン予想(が真であるという仮定)からわかります。さらに言えば(ここでは詳しくは解説しませんが)上の不等式はSchoenfeldさんによって精密化されており、(もちろんリーマン予想が真であるという仮定の上で)下のような不等式が成り立つということが知られています。実際$0\leq x\leq10000$において誤差(橙)とリーマン予想による評価(黄)をグラフにしてみるとこんな感じになります。またこの誤差のグラフ(橙)は一見ずっと正の値を取りそうに見えますが、実際はどこかで$0$になり負の値を取り、また正になっては負になってと振動することが知られており、さらにその振幅は段々大きくなって発散していくことがわかっています。というわけでリーマン予想からはその振幅の大きさの上界がわかることになるのでこれは非常に嬉しいのです。

素数とゼータ

スライド4
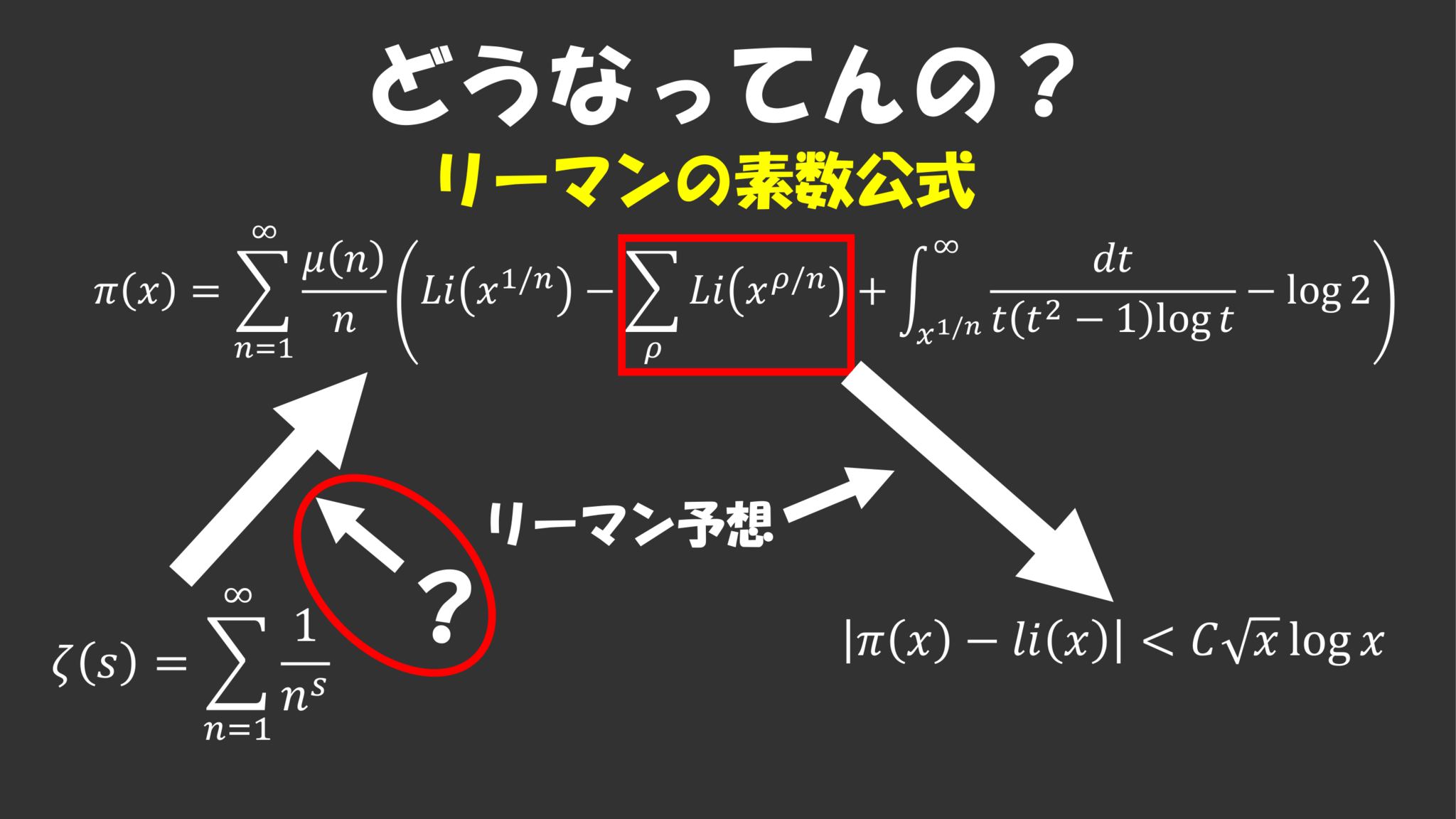
　というわけでリーマン予想から何がわかるのかということはわかりましたが、まだゼータ関数とリーマン予想と素数がどう繋がっているのかまではわかりません。とりあえずリーマンの素数公式における$\rho$はゼータ関数の非自明な零点のことを言っているので、ここにリーマン予想が作用することで不等式は示せそうな気はします。つまり今問題なのはゼータ関数からどうやって素数公式がわかるのか、ということになってきます。

スライド5
　それはまずオイラー積という素数でゼータ関数を表現した式から出発します。積の形だと使いづらいので対数を取ってなんだかんだすることで、素数の情報$\Pi(x)$からゼータの情報を引き出す式ができます。

スライド6
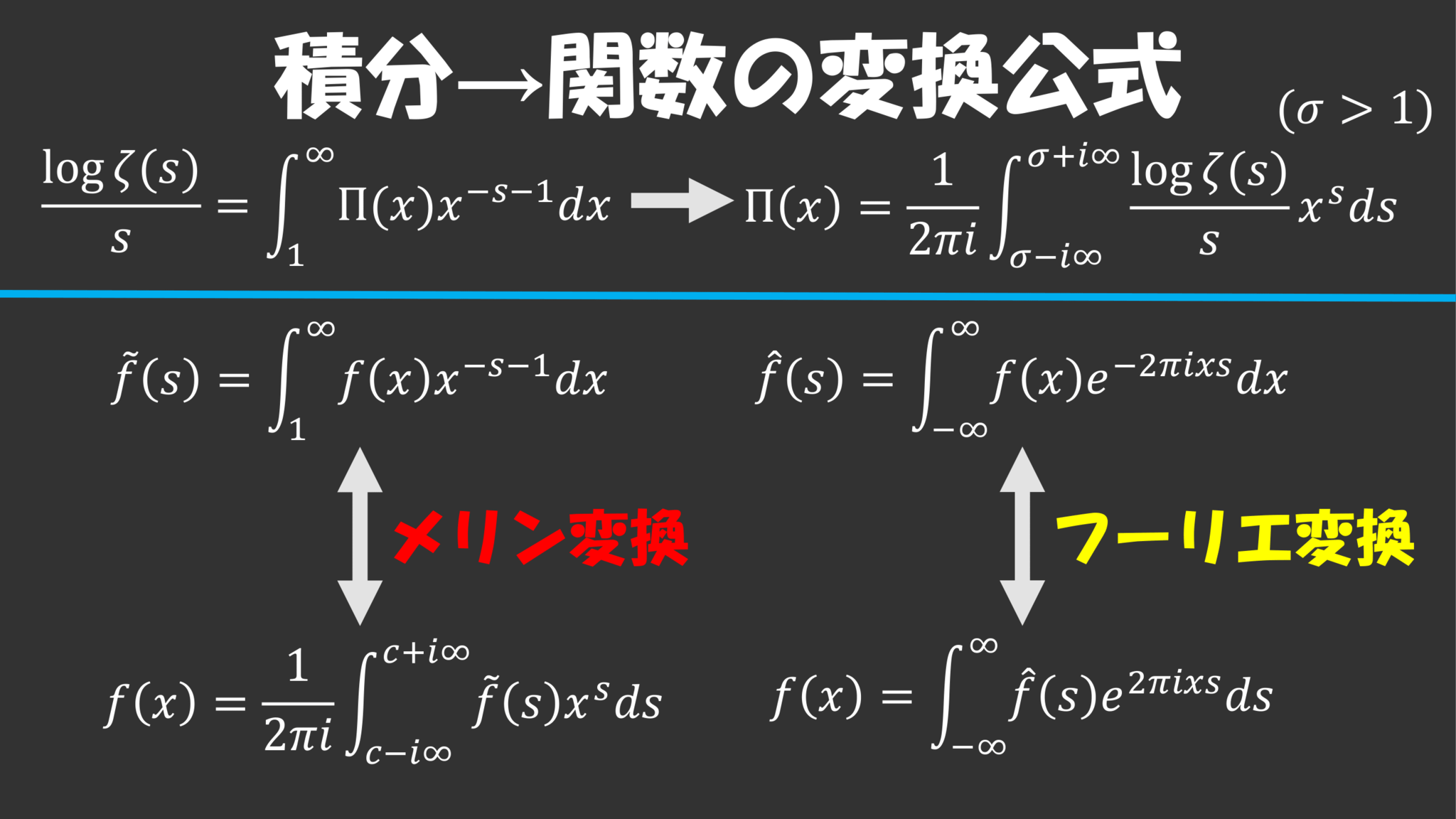
　ただ、今知りたいのはこの素数の情報$\Pi(x)$なので積分からこれを取り出す、ということをしたいわけです。積分から中身を取り出すと言えばフーリエ変換というものがありました。フーリエ変換$\hat{f}(s)$はまた積分をしてやることでその中身$f(x)$を取り出すことができます。そしてこの左の積分もメリン変換と呼ばれて同じように$\tilde{f}(s)$を積分してやることで中身$f(x)$を取り出せるのです($c$は$\tilde{f}(s)$が$\Re(s)=c$で定まる限り任意)。というわけでこれをさっきの式に適応することで$\Pi(x)$を取り出すことができたのですが、ここで注意してほしいのが元の式は$\Re(s)>1$でしか成り立っていないので$\s>1$ではないといけないということです。

スライド7
　とりあえずこうしてゼータから素数の情報を引き出す式が出来ましたが、この式はゼータ関数の$\Re(s)>1$の情報しか使っていません。しかしゼータ関数の零点は全部$\Re(s)<1$にあったのでこれだと零点の情報から素数の情報を引き出す式が作れそうにありません。そこで零点からゼータ関数を表現する式を考えたくなります。零点から関数を表現する、といえば因数分解というものがありました。因数分解と言えば多項式$f(x)$が$x=\a,\b,\g,\ldots$において$0$になれば$f(x)=(x-\a)(x-\b)(x-\g)\cdot$と表現できることを言いました。これはゼータ関数にも同じようなことができて、ゼータ関数の非自明な零点$s=\rho$と自明な零点$s=-2,-4,-6,\ldots$から(収束性とか色々考慮した結果)右下のような因数分解が成り立つことが知られています。

スライド8
　というわけで零点からゼータを表現する式、ゼータから素数(の情報)を表現する式ができたので、これを組み合わせて計算していった結果、下のような素数公式が得られることになります。

素数とリーマン予想

スライド9
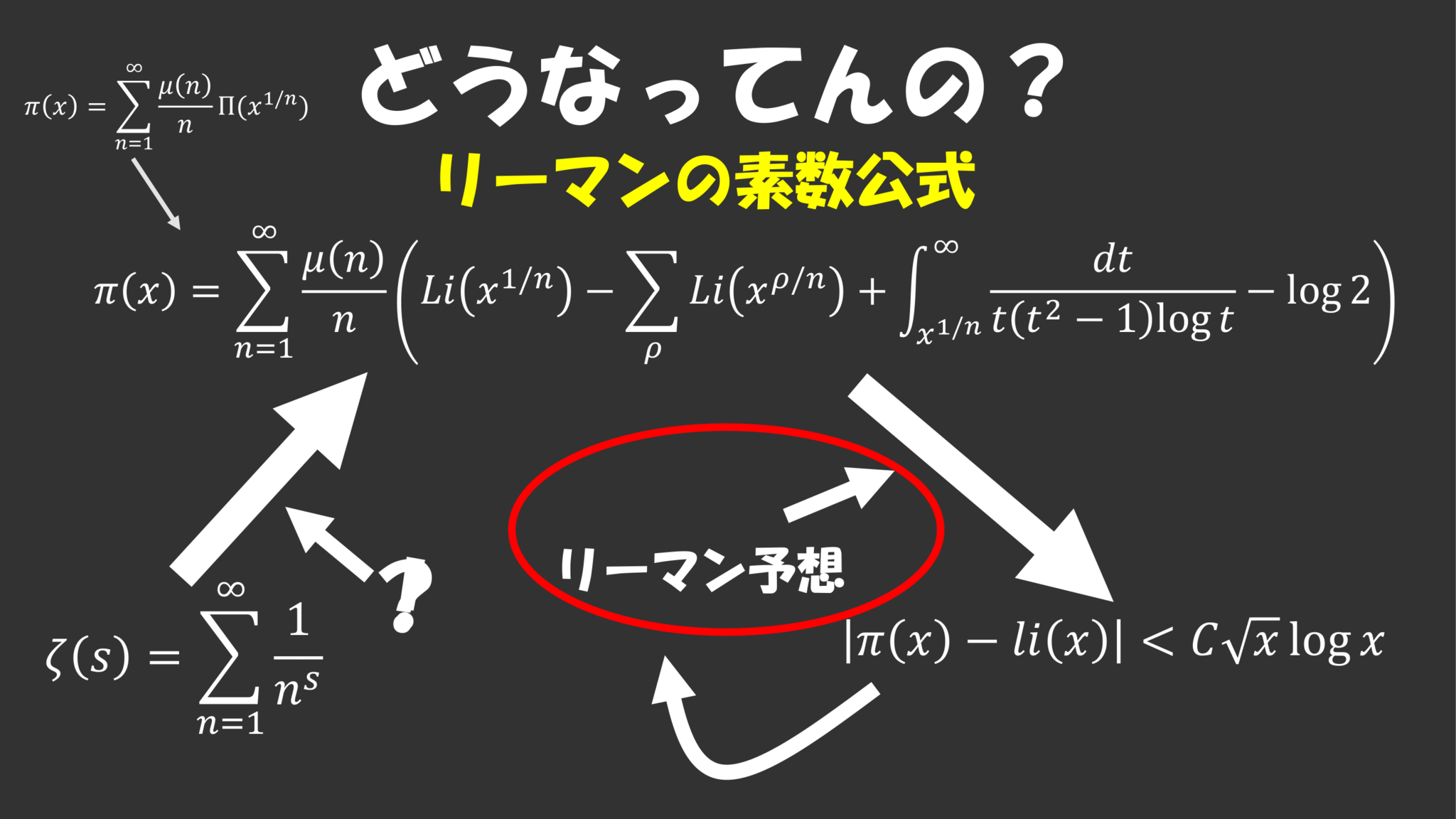
　というわけでゼータ(の零点)と素数とがどう繋がっているのかはわかりました。ちなみにさっきのは$\Pi(x)$の素数公式でしたが、メビウスの反転公式というもので$\Pi(x)$から$\pi(x)$を表現することができるので$\pi(x)$の素数公式を得ることができます。そして、次に問題になるのがリーマン予想からどうあの不等式が導かれるのか、ということになります。更に言うと実はこの不等式はリーマン予想と同値になっています。そのことについても一緒に解説していきましょう。

スライド10
　まずリーマン予想から不等式を導く流れを見ていきましょう。上の式は$\pi(x)$じゃなくて$\Pi(x)$を考えればいいということを書いています。いま、リーマンの素数公式から素数定理の誤差$\Pi(x)-\mathrm{Li}(x)$は次のように表現できました。ここで右の二項はおよそ$-0.7$から$-0.3$程度でほぼ無視できます。またLittlewoodの定理から左辺は振動しながら発散するということだったので$\sum_\rho\mathrm{Li}(x^\rho)$の項が振動項ということになります。
　いま対数積分$\mathrm{Li}(x)$は$x/\log x$と近似できるのでこれをさっきの級数に適用して指数を落とすと真ん中くらいの式のようになります。この右側の級数を$\rho$の大きさに応じて分け、一方は絶対値を中に入れてやるとリーマン予想の仮定から$|x^\rho|=x^{\Re(\rho)}=x^\frac12$となります。もしリーマン予想が成り立たないとすると$x$は$1/2$より大きくないといけません。
　また非自明な零点の分布についてはある程度わかっていて、どちらの値も$O(\log^2x)$となることがわかっています。そしてそれを$\log x$で割っていたので結局$|\Pi(x)-\mathrm{Li}(x)|=O(\sqrt x\log x)< C\sqrt x\log x$が成り立つわけです。

スライド11
　逆にその不等式を仮定するとリーマン予想が導かれることを示します。素数の情報からゼータの情報を引き出すと言えばオイラー積から導かれる次のような式がありました。さっきはこの式から素数公式、ひいては対数積分$\mathrm{Li}(x)$が出てきましたが、逆に$\mathrm{Li}(x)$をこの積分に入れることで$\log(s-1)$が出てくることになります(ただ$\mathrm{Li}(1)$が発散する都合でその等式は厳密には成り立ちません)。
　いま仮定より$|\Pi(x)-\mathrm{Li}(x)|< Cx^{\frac12+\e}$と評価できるので左辺の積分は$\Re(s)>\frac12+\e$、つまり$s$の実部が$1/2$よりちょっとでも右側にあれば収束することになります。
　ここで非自明な零点が$1/2$の右側にあったとすると$\log((s-1)\z(s))$が発散することになりますが、これは右辺が収束することに矛盾します。また非自明な零点$\rho$が$1/2$の左側にあるときゼータ関数の対称性から$1-\rho$も非自明な零点になりますが、$1-\rho$は$1/2$より右側にあるので矛盾します。ということで非自明な零点は全部$\Re(s)=1/2$に整列していなくてはいけない、つまりリーマン予想は真ということになります。

スライド12
　以上で話したいことは全部ですが、最後に今回出てきた式の関係をまとめておきましょう。まず最初にオイラー積から積分の式が出てきて、この積分の式とゼータ関数の因数分解から素数公式が、素数公式とリーマン予想から例の不等式が、例の不等式と積分の式からリーマン予想が導かれる。という構図になっています。

スライド13
　ご清聴ありがとうございました。