二つの円柱を合わせた図形

空間図形,重積分

はじめに

こんにちは、AGAです。
今回は初めての図の導入も含めた記事になっています。

本題

今回考えていくのは上半分が以下の図1のようになる立体です
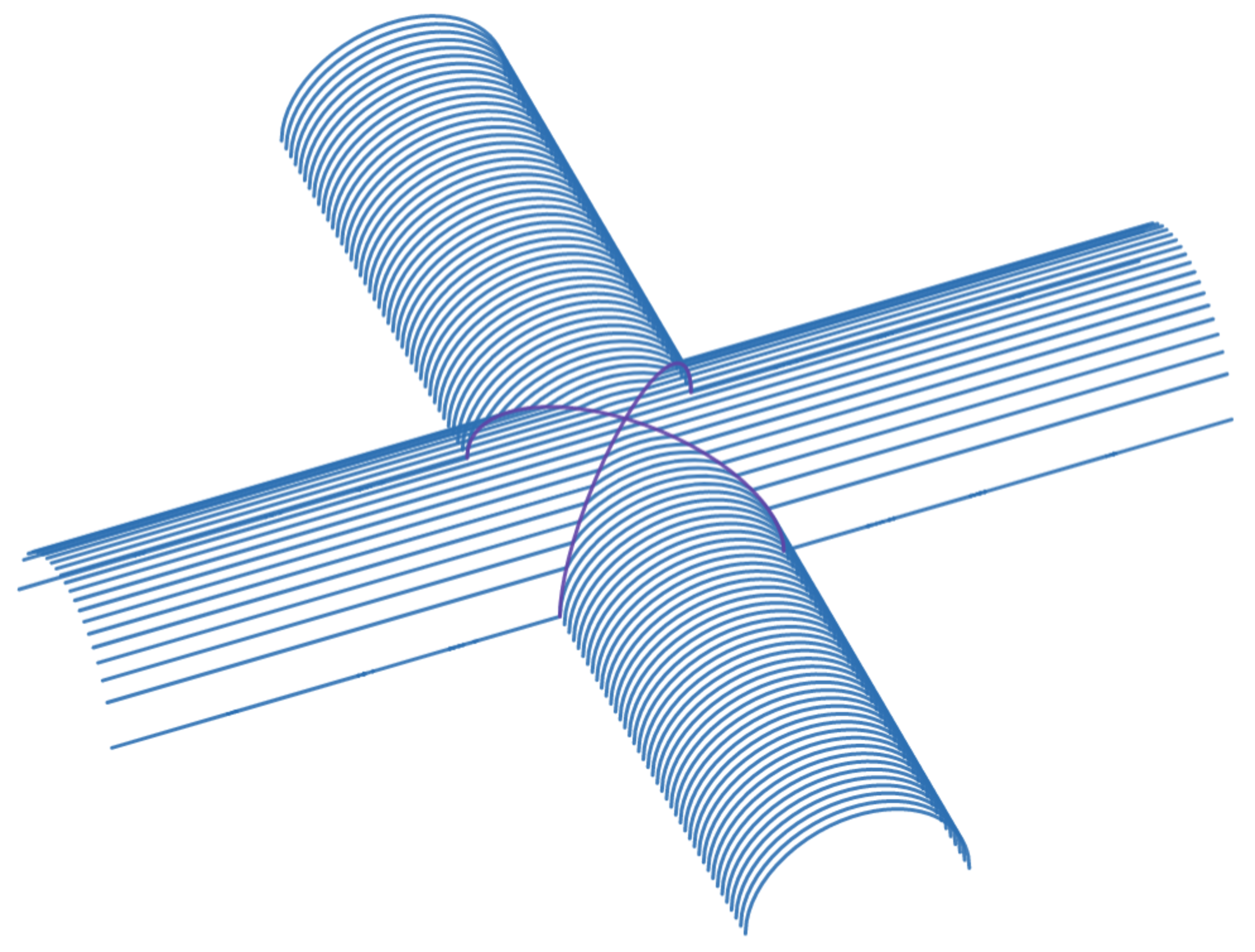二つの円柱を合わせた図形(紫は重なっている部分)

二つの円柱の式はそれぞれ $x^{2} + z^{2} = 1, y^{2} + z^{2} = 1$ とする。

定式化

この図形の式は
$min (x^{2}, y^{2}) + z^{2} = 1$

この図形は二つの円柱の合わせた図形であるから
和集合を考えると、
${(x, y, z) \in R^{3} | x^{2} + z^{2} \leq 1}$ と ${(x, y, z) \in R^{3} | y^{2} + z^{2} \leq 1}$
の和集合だから、 ${(x, y, z) \in R^{3} | x^{2} + z^{2} \leq 1 \lor y^{2} + z^{2} \leq 1}$
$= {(x, y, z) \in R^{3} x^{2} \leq 1 - z^{2} \lor y^{2} \leq 1 - z^{2}}$
$= {(x, y, z) \in R^{3} | min (x^{2}, y^{2}) \leq 1 - z^{2}}$
$= {(x, y, z) \in R^{3} | min (x^{2}, y^{2}) + z^{2} \leq 1}$
よってこの図形(の境界の面)の式は
$min (x^{2}, y^{2}) + z^{2} = 1$ となる。

体積

ここからは無限の円柱の部分を考えてもつまらないので、
$- 1 \leq x \leq 1, - 1 \leq y \leq 1$
の範囲で考える。

上記の範囲で
$min (x^{2}, y^{2}) + z^{2} = 1$ で挟まれた体積 $V$ は
$V = 4 π - \frac{16}{3}$

与式を変形する
$min (x^{2}, y^{2}) + z^{2} = 1$
$z^{2} = 1 - min (x^{2}, y^{2})$
$z = \pm \sqrt{1 - min (x^{2}, y^{2})}$
$z \leq 0$ の部分と $z \geq 0$ の部分の面積は等しい

このことから重積分を用いると次のようになる
$V = 2 \int_{- 1}^{1} \int_{- 1}^{1} \sqrt{1 - min (x^{2}, y^{2})} d x d y$
$\sqrt{1 - min (x^{2}, y^{2})}$ は偶関数だから
$= 8 \int_{0}^{1} \int_{0}^{1} \sqrt{1 - min (x^{2}, y^{2})} d x d y$
$= 8 \int_{0}^{1} ((\int_{0}^{y} \sqrt{1 - x^{2}} d x) + (\int_{y}^{1} \sqrt{1 - y^{2}} d x)) d y$
$= 8 (\int_{0}^{1} \int_{0}^{y} \sqrt{1 - x^{2}} d x d y + \int_{0}^{1} \int_{y}^{1} \sqrt{1 - y^{2}} d x d y)$
$= 8 (\int_{0}^{1} \int_{x}^{1} \sqrt{1 - x^{2}} d y d x + \int_{0}^{1} \int_{y}^{1} \sqrt{1 - y^{2}} d x d y)$
$= 16 \int_{0}^{1} \int_{x}^{1} \sqrt{1 - x^{2}} d y d x$
$= 16 \int_{0}^{1} (1 - x) \sqrt{1 - x^{2}} d x$
$= 4 π - \frac{16}{3}$

表面積

上記の範囲で
$min (x^{2}, y^{2}) + z^{2} = 1$ で挟まれた表面積 $S$ は
$S = 2 π$

表面積の公式から
$S = \int_{- 1}^{1} \int_{- 1}^{1} \sqrt{1 + (\frac{\partial z}{\partial x})^{2} + (\frac{\partial z}{\partial y})^{2}} d x d y$
$= \int_{- 1}^{1} \int_{- 1}^{1} \sqrt{1 + {(\frac{\partial}{\partial x} \sqrt{1 - min (x^{2}, y^{2})})}^{2} + {(\frac{\partial}{\partial y} \sqrt{1 - min (x^{2}, y^{2})})}^{2}} d x d y$
$= 4 \int_{0}^{1} (\int_{0}^{y} \sqrt{1 + {(\frac{\partial}{\partial x} \sqrt{1 - x^{2}})}^{2} + {(\frac{\partial}{\partial y} \sqrt{1 - x^{2}})}^{2}} d x + \int_{y}^{1} \sqrt{1 + {(\frac{\partial}{\partial x} \sqrt{1 - y^{2}})}^{2} + {(\frac{\partial}{\partial y} \sqrt{1 - y^{2}})}^{2}} d x) d y$
$= 4 \int_{0}^{1} (\int_{0}^{y} \sqrt{1 + {(- \frac{x}{\sqrt{1 - x^{2}}})}^{2}} d x + \int_{y}^{1} \sqrt{1 + {(- \frac{y}{\sqrt{1 - y^{2}}})}^{2}} d x) d y$
$= 4 \int_{0}^{1} \int_{0}^{1} \sqrt{1 + {(- \frac{x}{\sqrt{1 - x^{2}}})}^{2}} d x d y$
$= 4 \int_{0}^{1} \int_{0}^{1} \sqrt{1 + \frac{x^{2}}{1 - x^{2}}} d x d y$
$= 4 \int_{0}^{1} \int_{0}^{1} \sqrt{\frac{1}{1 - x^{2}}} d x d y$
$= 4 \int_{0}^{1} \int_{0}^{1} \frac{1}{\sqrt{1 - x^{2}}} d x d y$
$= 4 \int_{0}^{1} \frac{π}{2} d y$
= $2 π$