【祝アーベル賞受賞】ロバースの業績紹介 - クネーザー予想の解決
本記事は 物工/計数Advent Calender 2021 の23日目として書かれています.筆者は数理情報学専攻に所属するM2です.
はじめに
今年のアーベル賞にウィグダーソンと共同で選出されたラスロ・ロバース(Lovász László)はハンガリー出身の数学者です.受賞理由は「理論計算機科学と離散数学への基礎的な貢献と,それらを現代数学の中心的な分野に発展させる上で主導的な役割を果たしたこと」でした.過去にはウルフ賞数学部門(1999年),京都賞基礎科学部門(2010年)なども受賞しており,国際数学者会議(ICM)を主催する国際数学連合の総裁も務めた大人物です.
幼い頃から数学オリンピックで活躍し(金メダル3回と銀メダル1回),それを見た同じくハンガリー出身のエルデシュに声をかけられて離散数学の世界に入ったそうです.
彼には実に膨大な業績があり,例えば「数学セミナー」の
2022年1月号
にて代表的なものの紹介記事があります.その中には挙げられていない「クネーザー予想の解決」をここでは紹介しようと思います.解決した結果以上に,グラフ彩色問題に対して初めて代数的位相幾何学の手法を持ち込んだことが大変画期的です.
位相幾何学の起源はオイラーのグラフ理論的な発想による
ケーニヒスベルクの橋の問題の否定的解決
だとも言われるのに,グラフ理論が代数的位相幾何学の手法にそれまで縁遠かったのは不思議に思われるかもしれません.しかし,グラフは位相空間としては$1$次元の有限単体複体であり,それはブーケ(円周のウェッジ積)とホモトピー同値であまり面白くない対象なのです.代数・幾何・解析の世界では歴史的に直接の研究対象ではなく,複雑な構造を記述するための道具として使われてきました(e.g. 箙).実際,ロバースもグラフそのものではなく新たにグラフから抽象複体を構成することでホモトピーの意味ある議論をできるようにしています.
読者には予備知識としてグラフ理論と代数的位相幾何学の初歩を仮定しますので,不親切に感じたら申し訳ありません.彩色数や基本群がピンとくる方ならストーリーを理解するのに十分だと思います.
注) アーベル賞はノルウェー政府によりアーベルの生誕200年を記念して設立された賞で,2001年から毎年,年齢制限なく2~4名の受賞者を選出しています.高額な賞金もあって若手奨励を目的とするフィールズ賞よりもノーベル賞に近いでしょう.
クネーザー予想
以降は有限無向単純グラフのみを扱います.また,$[n]=\lbrace 1,2, \cdots ,n\rbrace$とします.
クネーザー予想はクネーザーグラフの彩色数についての予想ですから,まずはクネーザーグラフの定義を述べます.
$n \geq 2k\geq 2 $なる自然数$n,k$に対して,次の頂点集合と辺集合から定まるグラフをクネーザーグラフといい,$KG_{n,k}$とかく.
$$V(KG_{n,k})=\lbrace A\subset [n]\ | \left| A \right| =k\rbrace$$
$$E(KG_{n,k})=\lbrace \lbrace A_1,A_2\rbrace \ |\ A_1,A_2\in V(KG_{n,k}),\ A_1\cap A_2=\emptyset \rbrace$$
$KG_{n,1}$は完全グラフ$K_n$に同型であり,$KG_{5,2}$はピーターセングラフに同型である.
このグラフの彩色数について,上からの評価は容易です.
$$\chi (KG_{n,k}) \leq n-2k+2$$
$c:V(KG_{n,k})\rightarrow[n-2k+2]$を
$$c(A)=\min \lbrace \min_{a\in A} a,n-2k+2\rbrace$$
とすれば$(n-2k+2)$-彩色が得られる.$\blacksquare$
クネーザーはさらに踏み込んで1955年に以下の予想を発表しました.これを1978年に解決したのがロバースです.
$$\chi (KG_{n,k})=n-2k+2$$
注) 何とも紛らわしいですが本記事を通して$\chi$は彩色数を表し,オイラー標数ではありません.後で出てきますが,$G$もグラフと群で取り合いになってしまいます.
近傍複体
それでは次に,証明のあらすじを理解するための準備をしましょう.ロバースは頂点集合の部分集合であって共通近傍をもつものを単体として得られる抽象複体を考えました.
$G$を位数$2$以上のグラフとする.
次のように定まる抽象複体$N(G)$を近傍複体という.
$$N(G)=\lbrace A\subset V(G)\ | \bigcap_{v\in A}N(v) \neq \emptyset \rbrace$$
ここでグラフ$v\in V(G)$に対して$N(v)$は$v$の近傍のことである.すなわち,
$$N(v)=\lbrace u\in V(G)\ |\ \lbrace u,v\rbrace \in E(G)\rbrace$$
なお,$N(G)$の頂点集合は$G$の頂点集合$V(G)$から孤立点を除いたものとなる.
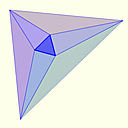
![文献[3]より引用](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20211212103159.png?alt=media) 文献[3]より引用
文献[3]より引用
完全グラフ$K_n$の近傍複体$\left| N(K_n)\right|$は標準単体$\Delta_{n-1}$の境界複体となる.
続いて,代数的位相幾何学に関するいくつかの定義を整理します.
ホモトピー群
$A \subset X$なる位相空間の組$(X,A)$を位相空間対と呼び,$2$つの位相空間対$(X,A),(Y,B)$について
$C((X,A),(Y,B))=\lbrace f:X\rightarrow Y|$$f$は連続,$ f(A)\subset B\ \rbrace$
と書くことにしましょう.このとき,高次ホモトピー群の定義は以下のように記述できます.
$n$を自然数とする.
$C((I^n,\partial I^n),(X,x_0))$のホモトピーによる商集合に対して次の積(から誘導されるもの)を定めてできる群を$n$次ホモトピー群といい,$\pi_n(X)$とかく.
$f\ast g(t_1,t_2, \cdots ,t_n)=\begin{eqnarray}
\left\{
\begin{array}{l}
f(2t_1,t_2, \cdots ,t_n) \hspace{ 26pt } (0\leq t_1\leq \frac{1}{2})\\
g(2t_1-1,t_2, \cdots ,t_n)\quad (\frac{1}{2}\leq t_1\leq 1)
\end{array}
\right.
\end{eqnarray} $
$1$次ホモトピー群とは基本群のことです.ちなみに,$2$次以上のホモトピー群は可換です.
基本群にとっての単連結性は高次ホモトピー群についても考えることができます.
$0\leq m\leq n$なるすべての$m$について
$\pi_m(X)=0$となるとき$X$は$n$-連結であるという.
これは以下とも同値である.
連続写像$S^m\rightarrow X$が常に$D^{m+1}\rightarrow X$へ連続拡張できる.
証明の大まかな流れ
これでひとまず準備が整いました.ロバースは次の$2$つの補題を組み合わせることで証明しました.
$G$を位数$2$以上の単純グラフとする.
幾何学的実現$\left|N(G)\right|$が$k$-連結 $\Longrightarrow$ $\chi (G)\geq k+3$
$\left|N(KG_{n,k})\right|$は$(n-2k-1)$-連結.
これらが揃えばクネーザー予想を証明できるのは明らかですので,補題の証明の概要に移ります.ただし,個別のグラフに対する結果である後者の証明は省略します.
前者の証明を見る前に,そこで用いられる概念について追加で二点説明します.一つ目は彩色のグラフ準同型による解釈です.
頂点彩色とグラフ準同型
$G,H$を単純グラフとする.
写像$\varphi:V(G)\rightarrow V(H)$が$G$から$H$へのグラフ準同型であるとは,任意の$u,v\in V(G)$について
$\lbrace u,v\rbrace \in E(G) \Longrightarrow \lbrace \varphi (u),\varphi(v)\rbrace \in E(H)$
が成り立つことをいう.
すなわち,隣接関係を保つような頂点間の写像をグラフ準同型と呼んでいます.すると,$G$から$K_n$へのグラフ準同型は$G$の$n$-彩色と対応しているとわかります.$V(K_n)=[n]$と考えたとき$k\in V(K_n)$のグラフ準同型による逆像を色$k$で塗ればよいわけです.したがって彩色数はグラフ準同型の言葉でかけます.
$\chi(G)=\inf \lbrace n\ |\ $$G$から$K_n$へのグラフ準同型が存在する.$\rbrace$
ボルスク-ウラムの定理と群作用
補足の二つ目として,ボルスク-ウラムの定理の変換群論的な言い換えを与えます.
連続写像$f: S^n\rightarrow \mathbb{R}^n$には$f(x)=f(-x)$となる点$x\in S^n$が存在する.
対蹠写像$S^n\rightarrow S^n ; x \mapsto -x$により$S^n$は$\mathbb{Z}_2$が自由に作用します.一般に群$\varGamma$が自由に作用する位相空間を$\varGamma$-空間といいますので,$S^n$は$\mathbb{Z}_2$-空間とみなせるということです.さらに,$\varGamma$-空間の間の連続写像のうち作用と可換であるものを$\varGamma$-(同変)写像といいますから,ボルスク-ウラムの定理は次のように変換群論の言葉でかけます.
$S^m$から$S^n$への$\mathbb{Z}_2$-写像が存在する $\Longrightarrow$ $m\leq n$
いよいよ補題の証明の概要に入ります.
注) ロバース自身は補題の証明にあたり変換群論的観点を表に出してはいませんが,ここではより現代的に簡潔化されたものを紹介します.
補題の証明のスケッチ
$N(G)$の重心細分の$\mathbb{Z}_2$-部分複体$L(G)$であって次の条件をみたすものが構成できます.ただし,頂点集合の部分集合に対してそれらの共通近傍をとる写像を$f$とすると$f^3=f$より$\mathbb{Z}_2$の作用を引き起こすことに注意します.
- $\left| L(G) \right|$は$\left| N(G) \right|$と同じホモトピー型をもつ
- 任意のグラフ準同型$f:G \rightarrow H$は$\mathbb{Z}_2$-写像$L(f):\left| L(G) \right|\rightarrow \left| L(H) \right|$を誘導する.
- $G\cong K_n$のときには$\mathbb{Z}_2$-同相$\left| L(K_n) \right|\rightarrow S^{n-2}$が存在する.
さて,$\chi(G)=m$とするとグラフ準同型$G\rightarrow K_m$が存在します.また(1)より$\left| L(G) \right|$は$k$-連結ですから$S^{k+1}$の単体分割を用いて帰納的に連続拡張することで$\mathbb{Z}_2$-写像$S^{k+1}\rightarrow \left| L(G) \right|$を構成できます.(2),(3)もあわせると次の$\mathbb{Z}_2$-写像の系列を得ます.
$$S^{k+1}\rightarrow \left| L(G) \right| \rightarrow \left| L(K_m) \right|\rightarrow S^{m-2}$$
これにボルスク-ウラムの定理を適用すると$k+1\leq m-2$より$\chi(G)>k+3$を得ます.$\blacksquare$
注) この補題の証明法は,グラフのなす圏から$\mathbb{Z}_2$-空間のなす圏への関手を構成することにより,$\mathbb{Z}_2$-写像の存在性をグラフ準同型の存在性に読みかてボルスク-ウラムの定理を移植したのだと総括できます.また,あまり詳しくないですが,これらの圏は適当なモデル構造によってQuillen同値となるそうです(圏同値ではない).
以上のように近傍複体は彩色数の評価に利用できますが,値の決定には向かない,すなわち近傍複体から定まる位相的不変量で特徴づけはできないことが知られています.次のようなことが起こるからです.
任意の自然数$m,n$に対し単純グラフ$G,H$が存在して
$N(G)\cong N(H)$かつ$\chi(G)=m,\ \chi(H)=n$となる.

これらのグラフから定まる近傍複体は同型だが,彩色数は左が$4$なのに対し右は$3$である.
なお,近傍複体を一般化した概念にはHom複体と呼ばれるCW複体があり,現在も活発に研究されています.
余談ですが,前述の通り完全グラフへの準同型と彩色数の対応があったので,その類似から,クネーザーグラフを使うと有理数に値をとる分数的彩色数が彩色数の一般化の一つとして定義できます.
$\chi_f(G)=\inf \lbrace \frac{n}{m}\ |\ $$G$から$KG_{n,m}$へのグラフ準同型が存在する.$\rbrace$
おわりに
筆者は代数的グラフ理論,特に群論を絡めたグラフ理論を研究中の身で,グラフ同型による不変量の解析を大テーマに据えています.(分数的)彩色数はグラフ不変量の一例ですし,グラフ準同型は研究において中心的役割を果たします.
本記事を書く動機は二つありました.一つは,修士での方向性を決めるきっかけとなった論文がロバースらにより書かれたものだったということです.その出会いがなければ今頃どんな迷走をしていたかわかったものではないので,恩義を感じずにいられません.もう一つは,学部時代に数学科で位相幾何学を勉強していたことからクネーザー予想の解決は自分にもってこいの題材だと思いました.だいぶ知識が抜け落ちていましたが.
離散数学は純粋数学者たちから長らく「おもちゃ」の扱いを受けていました.そこからの現代化にあたって根幹をなす貢献をロバースはしたのです.その点で開墾者という印象を強く持ちます.いつも大きな仕事に取り組んでいて,新たな分野を作り基礎工事を終えて定礎を置いたら別のテーマに移っていきます.それは大多数の平凡な研究者にとってはありがたい話ともいえて,僕もあわよくばそのおこぼれに与ろうとしている一人というわけですね.