哲学的視点からの直観主義論理入門 [前編]
こちらは、 ISer Advent Calendar 2021 24日目の記事です。長いので2つに別れていて、このページは前編です。後編は こちら です。
- 2022/01/14追記: 後編の公開に合わせて、後編に入れる予定だった内容を少し前編の最後に加えました。また、参考文献や表記の修正をしました。
はじめに
私は普段は大学で情報科学・計算機科学を学んでいますが、それはかりそめの姿で、世を忍びながら言語や論理の哲学について学んでいます。ありがたいことに世の中には様々な文献があり、今回はそれらを読んで勉強したことを自分なりにまとめてみました。とはいえ哲学が専門というわけではないので、書き方が良くないところや誤解があるかもしれません。みなさまからのご指摘をお待ちしております。
さてさて、本稿のテーマである直観主義論理(intuitionistic logic)については、既にネット上に様々な日本語の入門記事があり(e.g.
照井『直観主義論理への招待』
)、今更何か書くようなことがあるのかという気がしてきますね。しかしよくよく考えてみると、そのような記事はどれも「数理論理学」や「数学基礎論」の観点からのもので、哲学的な観点から説明がなされているものは少ないです(間接的に取り扱っている文献は実はたくさんありますが)。というか、そもそも高校や大学の教育課程において論理学は「ある種の数学」みたいな扱いをされることが多く、哲学的な文脈で論じられること自体あまり多くないというのが実情ではないかと思います。しかし実際は、現代的な論理学は20世紀初頭から始まり、フレーゲ・ラッセル・ウィトゲンシュタインといった哲学者の貢献の中で、分析哲学の主要な分野として発展してきた側面があります。そして、直観主義論理もそのような歴史の中に位置づけることができるでしょう。本稿のモチベーションを一言でいうなら、このような哲学の目線から論理学を見てみること、そしてもっと言えば、「論理の正しさ」に哲学の道具を使ってアプローチしてみること、ということになります。
古典命題/述語論理の証明論・モデル論や、健全性・完全性定理に多少触れたことがないと理解できない可能性が高いです。
また、哲学に関する前提知識は必要ありません(おそらく)。
分かっている人向けの説明
- 「金子先生や大西先生の文献を追いながら、ダメットの反実在論に関する議論をざっくり整理してスッキリしたい」という気持ちに突き動かされて書いた個人的なメモを、他人に見せられるように整形・拡張したものです。
- 今年言語哲学について学んだことのメモにもなっています。
直観主義論理とは
まず、今回のテーマである直観主義論理についての説明をしておきたいと思います(すでにご存じの方は次章に移ってくださって構いません)。いわゆる普通の論理学の体系、古典論理(classical logic)についての知識は前提としているので、知らない方は色々調べて見てください。
さて、直観主義論理を非常に簡単に説明するなら、古典論理のうち一部の推論規則を「正しくない」とする論理といえます。ではどのような推論規則が正しくないとされるかというと、例えば以下のようなものが挙げられます。
- 排中律(the law of excluded middle): 任意の論理式$A$について、(仮定なしで)$A\lor\lnot A$を導いてよい
- 二重否定除去(double negation elimination): 任意の論理式$A$について、$\lnot\lnot A$という仮定から$A$を導いてよい
多くの人は、(意識はしていなくても)このような推論規則を利用しているでしょう。たとえば高校数学なんかで紹介されるのは、「○○ではないと仮定する。すると矛盾する。よって○○である。」という形の証明です(これを帰謬法(reductio ad absurdum)ともいいます)。これは、形式的に表現すると二重否定除去を利用していることが分かります。すなわち、
- ○○ではないと仮定する($\lnot A$)
- すると矛盾する$(\bot)$
- $\lnot A$という仮定が間違っていたことになるので、$\lnot\lnot A$が導かれます
- よって○○である($A$)
- これは$\lnot\lnot A$から$A$を導いています
ということです。「なんだ、そんなの当たり前じゃないの?」と思う方も多いかもしれませんが、「実はこのような証明はちゃんとした証明にはなっていないよ」とするのが直観主義論理の立場です。
古典論理の何が気に食わないのか
では、なぜわざわざこのような一見「当たり前」の推論を、直観主義論理は批判するのでしょうか?そこでキーとなる概念は「構成」です。
構成
そもそもなぜ私たちは証明を書くのでしょうか?レポートの問題で出されたから、という答えもあるかもしれませんが、真摯に答えるのであれば「読み手をあることについて説得するため」でしょう。例えばピタゴラスの定理は、主張を読んだだけでは本当に成立するのかよく分かりませんが、証明を提示されることでその正しさに納得できるわけです。では証明の「説得力」なるものはどこから来るのでしょうか?直観主義論理はそれを「(数学的)構成(construction)」という概念で説明しようとします(ここでの説明は[大西2021]に則っています)。
ここでいう構成とは、「実際にその正しさを示すなにかを作って見せること」です。例えば、「任意の整数は2で割り切れる」ということに反論したければ、実際に2で割れない整数を作って見せればよいでしょう。また数学の例ではないですが、「白いカラスがいる」ということを他人に納得させたかったら、本当に白いカラスを連れてくればよいわけです。
さて、このように証明の本質は「構成」という概念である程度捉えられているように思えます。となると、この考え方を逆にとれば、「構成ができていないんだったらそれは説得力を持たない」ということになるでしょう。直観主義論理がターゲットにするのは、まさにこのような「非構成的な」証明です。
非構成的な証明
非構成的とは?というイメージをつかむために、2つほど例を挙げてみます。
以下のような問題と、それに対する解答を考えてみましょう(非常に有名な例で知っている人も多いかもしれませんが、紹介しないわけにはいかないので書きます)。
- 問題: $a^b$が有理数となるような無理数$a,b$が存在する
- 証明: $\sqrt{2}^{\sqrt{2}}$は有理数または無理数である。これをもとに、以下のように場合分けをする。
- $\sqrt{2}^{\sqrt{2}}$が有理数である場合、$a=b=\sqrt{2}$とすれば、これらが条件を満たす無理数$a,b$を与える。
- $\sqrt{2}^{\sqrt{2}}$が無理数である場合、$a=\sqrt{2}^{\sqrt{2}},~b=\sqrt{2}$とすれば、$a^b=(\sqrt{2}^{\sqrt{2}})^{\sqrt{2}}=(\sqrt{2})^2=2$となり、$a^b$が有理数となる。よってこれらが条件を満たす無理数$a,b$を与える。
ふむふむ、と納得しそうになりますが、ちょっと待ってください。この証明を見ても、私たちは$a^b$が有理数となる無理数$a,b$が具体的に何なのか、知ることができません。2通りの場合が示されているものの、そのどちらに従えばよいかについて、この証明は何も言及していないのです。具体的な$a,b$が「構成」されていない、ということですね。これで「存在する」ということを「証明した」と言えるのだろうか、というのが素朴な疑問として生じてくるわけです。
数学の例ばかりでもアレなので、日常的な推論の例を挙げてみましょう。古典論理主義者Aさんとその友人Bさんの会話を考えます。
- A「忘年会の幹事やってくれない?ほかにやってくれそうな人がいなくてさ」
- B「う~ん幹事か、やりたくないってわけじゃないんだけど...」
- A「え、じゃあやりたいってこと?」
- B「いや、そうは言ってなくない?」
Bさんの「やりたくないってわけじゃない($\lnot\lnot A$)」という発言から、Aさんは二重否定除去を使って「やりたい($A$)」を導いていますが、Bさんはその結論を受け入れることに対して拒否感を示しています。素朴な感覚として、上のような二重の否定がつくと、(それがない場合よりも)何か「弱い」主張になります。ですから、「やりたくないってわけじゃない」だけでは、積極的に「やりたい」というだけの根拠が「構成」できていないわけです。
ではこのような非構成的な証明はなぜ批判されなければならないのでしょうか?このような疑問に答えつつ、これ以降の話を見ていきましょう。
補足
「直観主義論理」という名前を見ると、「直観主義」という思想的な立場に基づいているんじゃないかと思うかもしれませんが、そうとは限りません。
まず前提として、直観主義(intuitionism)というのは、実際に存在する立場です。これは、いわゆる「数学基礎論」という分野における一つの立場であり、オランダのブラウワーという数学者が提案したものです。ざっくり言うと数学とは「人間の心的な活動の産物である」という考え方をして、そこから数学を改めて基礎から考え直そう、という立場をとっています。この考え方自体はあまり多くの人に受け入れられていなかったようですが、ハイティンクなどのブラウワーの弟子により「直観主義論理」という論理体系が整備されると、構成的数学・計算機科学などとの関連の中で、それ自体興味深い数学的対象として研究されるようになりました(このあたりの話は今回は深入りしません)。
このように直観主義論理はもともと直観主義から出てきた立場ですが、直観主義の立場からしか正当化できないわけではありません。むしろ、直観主義というウケが悪い立場を離れて、全く別の方向性から直観主義論理を擁護したのがダメット(Micheal Dummett)というイギリスの哲学者です。本稿は主にこの人の議論に基づいています。
議論の見取り図
再度整理すると、本稿の焦点は「古典論理を批判して直観主義論理を擁護するためには、どのような議論がありうるか」ということです。よって、さしあたってのゴールを「古典論理に特徴的な推論規則を批判すること」としましょう。そうすると目標は、例えば上に挙げた排中律などを「正しくない」と批判すること、となります。
そしてこれをきちんと議論するためには、非常に込み入った議論を追っていく必要があります。木を見て森を見ず状態になると良くないので、詳細に入る前に、議論全体の「見取り図」みたいなものを説明しておきたいと思います。
推論規則に関する論争
まず、ある推論規則が正しくないと言うためには、何を根拠にすればよいでしょうか?導入のところで「構成」うんぬんの話をしましたが、それだけでは話がふわっとしていてあまり説得的ではないでしょう。この話をうまく進めるためには、そもそも推論規則について「正しい」とか「正しくない」とか言うための方法を考えなければなりません。
推論規則 → 意味論
一般に推論について正しい・正しくない、というとき、論理学ではどのような道具立てを使うでしょうか?例えば、次のような形式の推論を考えてみましょう(ここで$A,B$は任意の論理式を表すメタ変数です)。
$$
\dfrac{A\lor B}{A}{}
$$
これが正しくないことは、しばしばなんらかの意味論(semantics)を用意して、健全性定理(soundness theorem)によって示される、というのが論理学の授業のよくあるルートだと思います。健全性定理とは、適当な証明論・意味論に対して成り立つ以下のような定理です。
$\varGamma\vdash A$ならば$\varGamma\models A$
例えば上の例が正しくないことを、通常の古典論理の真理値(truth value)による意味論を使って示してみましょう(true/false, 1/0のアレです)。
ある2つの命題変数$p,q$に対して、付値$v$を$v(p)=0,~v(q)=1$と定めます。このとき、$v(p\lor q)=1$ですが$v(p)=0$です。よって、前提が真なのに結論が偽になってしまうような付値が存在するので、$p\lor q\not\models p$です。これと健全性定理の対偶から、$p\lor q\not\vdash p$です。以上より、上の例の推論は一般には成り立ちません。
こんな感じですね。もちろん、推論規則の「正しくなさ」を別のルートで証明する方法もあるにはあるのですが、この意味論による方法が割と一般的でしょう。というわけで、「推論の正しさを意味論でもって批判する」というルートを使ってみようか、ということになります。
意味論
さて、しかしながら、先ほどの例で用いた真理値による意味論では、たとえば排中律や二重否定除去則は妥当になってしまいます。よって、古典論理の批判という今回の目的には反してしまいますね。ですから、真理値による意味論(より一般に、述語論理も視野に入れると「モデル」による意味論)を批判する必要があります。ここで、議論のレイヤーが1個上に上がりました。推論規則に関する論争の決着を、意味論に関する論争によってつけるわけですね。
モデル
さて、ここで「モデル」による意味論(モデル論的意味論(model-theoretic semantics))について多少の説明をしておきましょう。名前は固いですが、ふだんの論理学に出てくるやつのことなので身構えなくても大丈夫です。
まずモデルというのは、イメージとしては「論理式の真偽を決めるための具体的な状況」という感じです。それ自体としては単なる記号である論理式に対してモデルを与えることで、私たちは論理式に対する具体的な意味(真偽値)を得ることができます。例えば標準的な古典述語論理の意味論を考えてみましょう。このような意味論では、何らかの集合である「領域(domain)」と、領域に定数や関数記号を割り当てる「解釈(interpretation)」が与えられます。例えば、論理式$P(c)\to Q(c)$に対して以下のようにモデルを与えることができます。
モデル$\mathcal{M}$を以下のように与える。
- 領域: $D=\left\{0,1,2\right\}$
- 解釈:
- $[\![c]\!]=0~(\in D)$
- $[\![P]\!]=\left\{0,1\right\}~(\subset D)$
- $[\![Q]\!]=\left\{0,1,2\right\}~(\subset D)$
このようなモデル$\mathcal{M}$のもとでは$P(c)\to Q(c)$は「真」になります($\mathcal{M}$はこの論理式を充足(satisfy)します)。そしてこのことは「モデル$\mathcal{M}$によって設定された状況に照らし合わせれば$P(c)\to Q(c)$が正しい」と説明できるでしょう。
ここでのポイントは、モデルは論理式の「構文」の世界から見れば外的なモノだということです。論理式(より一般に言語表現)はそれ自体では単なる記号列だから、その「外側」にあるモデルによって対応する意味を割り当ててうまく「解釈」しよう、そしてそうすれば、妥当性などの意味にまつわる性質を説明できるようになる、というのがモデル論的意味論の立場なわけですね(こんなの当たり前だと思うかもしれませんが、それは多くの論理学の授業でモデル論的意味論しか扱われないからでしょう)。
さて、以上で「モデル」というもののイメージを説明しました。そして再びにはなりますが、このようなモデル論的意味論では古典論理が批判できない(正しくは、今回の議論の方向性では批判しにくい)ので、本稿の目的には反するわけです。よって、モデル論的意味論を批判したうえで、その代替案を考えなければならないわけですね。そしてそこで登場するのが「証明論的意味論」というものです。詳しくは後述します。
意味論 → 意味理論
さて、そうするとこんど問題になるのは、モデル論的意味論とその代替案となる意味論、どちらを採用すべきなのかということです。ここで議論のレイヤーがさらに1つ上に上がりましたね。ある意味論を批判してある意味論を擁護するためには、どのような議論をすればよいでしょうか?
このことを議論するためには、「言葉の「意味」とは何なのか」という問いに答えなければなりません。なぜなら、意味論の適切さを議論するためには、そこで想定されている「意味」という言葉が何を意味しているのかをはっきりさせなければならないからです。このような言葉(自然言語)の「意味」一般に関する説明を与える理論を意味理論(meaning theory)といいます。ややテクニカルタームが紛らわしいですが、「意味論」に関する論争を「意味理論」に関する論争に帰着させるわけです。
意味理論
さて、「意味理論」すなわち「言葉の意味とは何か」のレベルにまで話がもつれこんできました。
「○○とは何か」という問いの形式から察せるように、この問いはもはや哲学的です。そして、このような議論を行ってきたのは言語哲学(philosophy of language)という分野です。今は議論の流れを説明するだけなので詳しいことは言いませんが、モデル論的意味論は、真理条件(truth condition)による意味理論によって支持されます(されえます)。そしてそれを批判する一つの立場として、検証主義(verificationism)的な意味理論があります。今はこのような用語があるんだなくらいに思っておいてもらえれば大丈夫です。
まとめ
というわけで、話のレイヤーがどんどん上にあがってきて、形式論理学からなんと言語哲学にたどり着いてしまいましたね。しかし、話の流れそのものは単純です。以上の過程を逆順にたどってトップダウンに議論を作っていけば、古典論理に対する批判ができることになります。これを表にすると下のようになります(大西先生の2021年の講義スライドの説明を改変したものです)。
| 批判対象 | 代替案 | |
|---|---|---|
| (自然言語の)意味理論 | 真理条件による意味理論 | 検証主義的な意味理論 |
| (形式論理の)意味論 | モデル論的意味論 | 証明論的意味論 |
| 推論規則 | 古典論理 | 直観主義論理 |
ちょっと長くなってしまいましたが、以上で大まかなストーリーは説明できたかなと思います。では、議論の内容に入っていきましょう。
step 0. 証明体系の準備
ちょっと話がそれますが、話の前提をはっきりさせるために、今回使う証明体系(自然演繹)についての説明をちょっと挟んでおきます。基本的な話しかしないので、もう知っているよという方は次の章に飛んでもらってかまいません。
構文
今回は命題論理の範囲だけで話をします。論理式の定義は通常通りです。以下のように帰納的に定まる最小の集合を論理式の集合$\mathrm{Fml}$とします。
- 加算無限個の命題変数$p_0,p_1,\ldots$があり、これらは$\mathrm{Fml}$の元である
- $\bot\in\mathrm{Fml}$である
- $A,B\in\mathrm{Fml}$ならば、$A\land B,A\lor B,A\to B\in\mathrm{Fml}$である
また、今回は否定を$\lnot A := A\to\bot$で定義します。
直観主義論理: NJ
今回は自然演繹(natural deduction)という証明の方式を使います。それぞれの論理結合子には、その結合子を含む結論を導く導入則(introduction rule)と、その結合子を含む前提から結論を導く除去則(elimination rule)があります($\bot$は例外で、導入則がありません)。直観主義論理に対する自然演繹の体系をNJといいます。推論規則の紹介だけします。
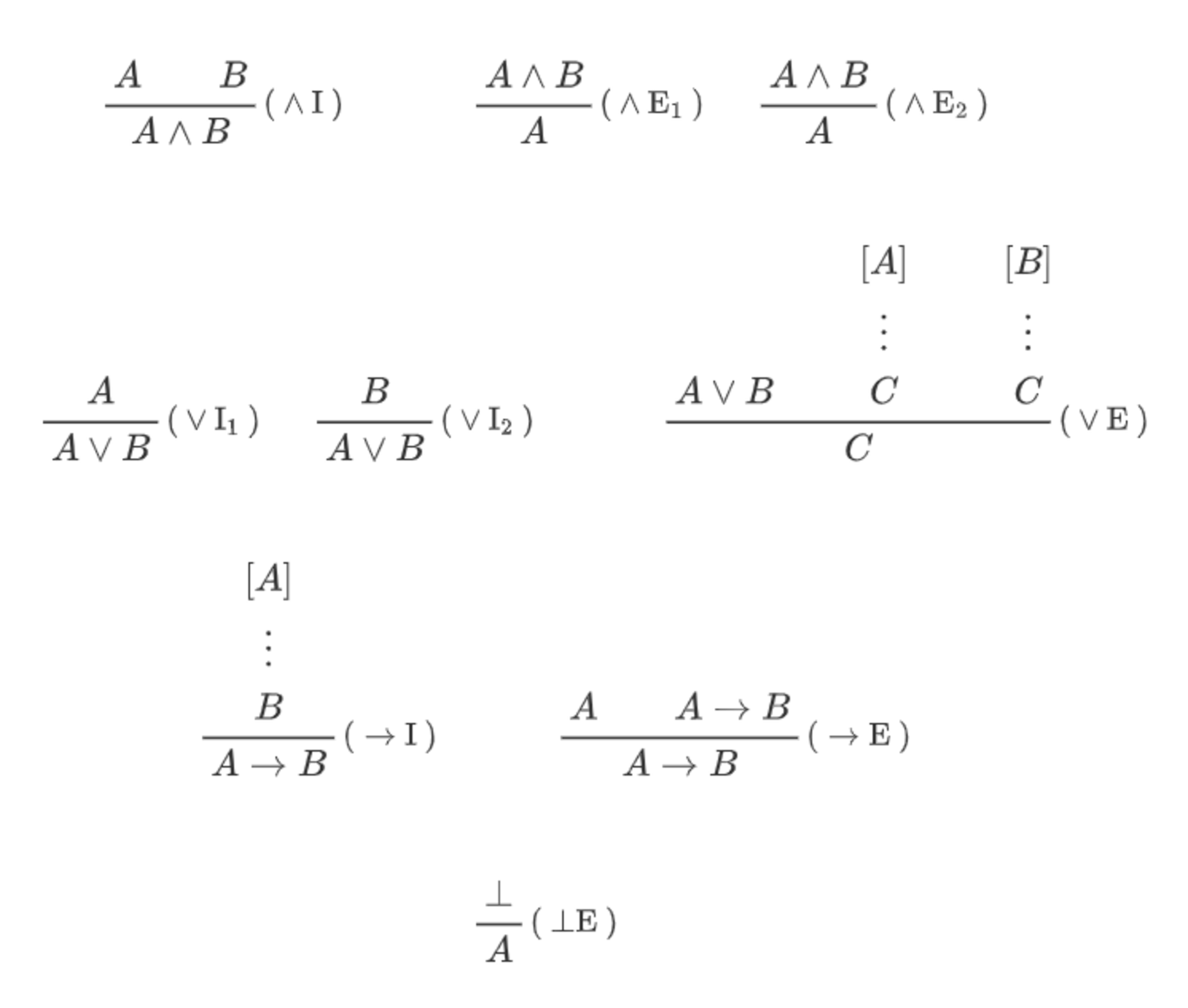
それぞれの$A,B$などはメタ変数であり、$\mathrm{Fml}$の任意の論理式が入ります。また、$[A]$などで表されているのは証明における仮定(assumption)であり、当該の推論規則を適用することで解消(discharge)されます。
古典論理: NK
NJに特定の推論規則を追加したものが古典論理の証明体系NKです。今回は、以下のような推論規則(排中律)を追加することにします。
$$ \begin{align*} \dfrac{}{A\lor\lnot A}{\small\mathrm{(LEM)}} \end{align*} $$
step 1. 真理条件による意味理論への批判
では最上位のレイヤーの議論、自然言語の意味理論に関する議論を見ていきましょう。先述の通りこの辺は言語哲学の話になるので、ふだん数学や計算機科学とかをやってる方には苦しいかもしれませんが、できるだけ頑張って平易に説明していきたいと思います。ただし、私なりの理解を書いて説明しているにすぎないので、ふだん分析哲学をやっている方からすると、誤った解釈・標準的ではない説明をしているところが見つかるかもしれません。ご指摘をお待ちしております。
なお、以下での説明は主に[ライカン 2006]を参考にしています。ダメットの議論については[ダメット 1990][金子 2006][大西 2012]あたりを見ながら書きました。
意味の事実
「言葉の意味って何だろう?」という問いは、なんだか漠然としていて、捉えどころがないような感じがします。このままウンウン考えても埒が明かないので、ある糸口を出発点にしてみましょう。それは、「言葉の意味とは何かという問いに答えるにあたって、私たちは意味に関する事実を説明できなければならない」ということです。物理や化学に喩えてみましょう。古典力学や化学反応のような理論は、実験・観察といった現実のデータを説明できるように設計されます。これと同様に、意味に関する哲学的理論も、現実の「意味」という概念に関するデータを出発点にすることになるわけです。
では、このような意味の事実として、どのようなものがあるでしょうか?例として、以下のようなものを考えてみます。
特定の記号列や音声の列が、意味を持ったり持たなかったりします。例えば「雪は白い」は有意味で、「は雪い白」は無意味です。この違いは何でしょうか?
- 同義性: 異なる記号列が、同じ意味を持つことがあります。
- 曖昧性: ある記号列が、異なる意味を持つことがあります。
意味と意味の間に「含む」という関係がある場合があります。例えば「数学の教員」という言葉の意味の中には、「教員」ということが「含まれて」います。あるいは特殊なケースとして、$A\land B$からは$A$が「含意」されます。これをどう説明できるでしょうか?
私たちは、これまで見たことがないような文・誰も発したことがない文であっても、その意味を(比較的簡単に)理解できます。例えば「緑のiPhoneが東急ハンズで売られている」という文を今この瞬間まで見たことがある人はおそらくいないと思いますが、しかしこれを読んだ方は意味を理解できたでしょう。これはどうしてでしょうか?
このような事実をうまく説明できるか?という観点から、いくつかの理論を見ていきましょう。最初に紹介するのはやや変わった(しかし重要な)説です。
意味の使用説
言語に関する基本的な事実として、「人間は言語を介して色々なことをする」「社会の中で複数の人間が言語を使ってやりとりできる」ということがあります。もちろん、形式的な記号として(まさに論理学のように)操作されることもありますが、それは教室で行われるような、本当に限られた言語実践の一側面を捉えているに過ぎません。
では、この「人間が言葉を使う」という観点から、いくつか言葉についての観察をしてみましょう。
私たちは朝ごろ人にあったとき「おはようございます」と言いますが、「おはようございます」に「こんばんは」で返事をしたら明らかにおかしいです。また、日本語を習いたての人が「昨日はカレーを食べたでした」と言ったとしたら、標準的な日本語話者は「「食べました」ですよ」と訂正するでしょう。このように、言葉には適切な使い方とそうではない使い方があり、適切な使い方の「規則」に従うことで、我々はコミュニケーションができます。そしてこのような規則は、社会全体である程度共有されているでしょう。言葉のこのような側面を、言語の規範性(normativity)ということがあります。
再び「おはようございます」という挨拶を考えましょう。これは、単体で何かを「意味」しているというより、他人に対して友好的に接するための合図のようなものであると言えます。もう少し複雑な例として、AさんがBさんに幾ばくかお金を借りて「明日までにお金を返すよ」と約束するとしましょう。この発言は、Aさんが「自分がいま約束をしている」と冷静に状況を分析して記述している、というよりは、むしろBさんに対して「お金を返す」という約束をするために「明日までにお金を返すよ」という文を使っていると言えます。このように「言語を使って何かをする」ことを、言語行為(speech act)といいます。
これらの観察をまとめると、「言葉は、慣習的な規則に従って使用される、社会的な道具である」ということが言えそうです。
このことはしばしば、チェスの駒に喩えられます。「ルーク」という駒を特徴づけるのは、開始時にどこに置くか・ゲーム中でそれをどのように動かしてよいかといった、チェスのルールで取り決められた「規則」です。同様に、言語表現を特徴づけるのも、その正しい使い方を定める慣習的な規則だ、というわけです。
このようなことから考えると、我々が「言葉の意味」といっているものは、実はその言葉の「使い方」なんだと言ってしまってよいのではないか、という気になってきます。例えば、意味の事実について以下のような説明ができます。
- 有意味性: 有意味な言葉とは、実際に私たちがそれを使うための規則が存在するような言葉です。
- ちょっとした例を挙げてみます。100年前であれば「スマホ」はまったくもって無意味だったでしょう。しかし、令和に生きる私たちはどのような状況で「スマホ」という語を使うのが適切かが分かっています。それがまさに有意味性のことなのだ、というわけです。
- 同義性: 意味が同じ言葉は、使い方が同じだといえます。
- 曖昧性: 複数の意味を持つ言葉は、複数の異なる使い方をされるといえます。
以上のような観察から、「言葉の意味とは、その使い方(use)である」という発想が出てきます。これを意味の使用説(use theory of meaning)といいます。
意味の使用説は、主にウィトゲンシュタイン(Ludwig Wittgenstein)という哲学者に由来しているとされています。あの「語りえぬものについては~」で有名な人ですね。ただし、語りえぬもの云々の話は「前期」と呼ばれる頃の哲学で(『論理哲学論考』)、後年になってから本人が「やっぱりあれはダメだった」と前期思想を徹底的に批判していきます(『哲学探究』)。この後期ウィトゲンシュタインは人間の言語活動をゲームにすることになぞらえ、言語ゲーム(language game, Sprachspiel)という概念を起点に、言葉や規則そのものに関する考察を進めました。その中で出てくるのがこの意味の使用説なわけですね。
さて話を戻しましょう。このように「意味=使い方」、という大まかな方針が得られたものの、以下のような疑問が残ります。
- 「誰も発したことがないような文も理解できる」という能力は、どのように説明できるのでしょうか?言葉の用法が慣習的な規則で定まるのだとすれば、このような「誰も発したことない文」の規則・使い方とは何でしょうか?そんなものが決まっているのでしょうか?
- 言葉の意味がその使い方である、という考え方は、例えば個別の単語についてはどのように適用できるのでしょうか?例えば「ウィトゲンシュタイン」という固有名詞の意味は、とても素朴に考えればウィトゲンシュタインというその人のことではないかという気がしてきます。これを「使い方」によって説明することはできるでしょうか?
これに応答がしにくいのは、意味の使用説がある種のスローガンだからです。言葉の意味というものを捉える大まかな方針は与えてくれるものの、個々の単語・文の意味を具体的にどう説明するかについては特に言及していません。ですから、さらなる説明のためには、使用説をベースとして何らかのメカニズムを取り入れて理論を拡張する必要があります。これについては後程詳しく説明します。
とはいえ、「人間が言葉を使う」という観点からの考察じたいは、言葉の意味を考える上では無視できないように思われます。ということで、今回のこれ以降の議論は、この意味の使用説を基本テーゼとして進めていきたいと思います。
意味の指示説
というわけで意味の使用説というものを導入しましたが、なんだか急に突飛な話が出てきてびっくりしたかもしれません。もっと素朴に考えてもよいんじゃないの?という気もしてきますね。
というわけで別の説を紹介していきましょう。良くも悪くも「常識的」な考え方として、次のようなものがあります。例えば、
- 「ポチ」という名前(固有名詞)の意味は、それが指し示すポチという犬のことだ
- 「犬」という名前(一般名詞)の意味は、犬の集まりのことだ
という感じです。このように指示(reference)や表示(denotation)の関係によって言葉の意味を説明する理論を意味の指示説(referential theory of meaning)といいます。
さて、「良くも悪くも」という言い方から察せるかもしれませんが、この説には多くの批判があります。一部の例を挙げるならば、
明らかに指示対象を持たない言葉が存在します。
- 例えば、英語の"nobody"は指示対象を持ちません。
- 「現在のフランス国王は禿である」という文を考えましょう。「現在のフランス国王」に対応する対象は存在しませんから、意味の指示説に基づけばこの文全体も無意味ということになってしまいますが、どうもそうは思えません。
言葉の指示対象は名詞については分かりやすいものの、そのほかの品詞についてはどうでしょうか。例えば、英語の"the"という冠詞や日本語の「は」という助詞が「指し示すもの」とは一体何でしょうか?
意味を「指示」や「表示」によって説明する理論を擁護するためには、少なくとも上の2つの疑問に応答する必要があります。
真理条件による意味理論
このような「意味の指示説」の困難を乗り越えた理論として、真理条件による意味理論があります。そしてこれが今回一番反論したい相手になります。敵を知らなければ戦いようはありませんから、じっくり見ていきましょう。
まず、真理条件(truth condition)という言葉に耳なじみがないかもしれません。ある文の真理条件とは「その文が真になる条件」のことです。そのまんまですね。例えば「東京は晴れである」が真になるのは、実際に東京の天気が晴れになっているような状況が成り立っているときであり、これがまさに真理条件です。
真理条件による意味理論では、文の意味とはその真理条件であると説明されます。「文の」という限定を付けたのは、例えば名詞や動詞といった単語に対しては、「文の意味=真理条件」というコアの主張に合うように意味が割り当てられていくからです。これについてはもう少ししてから説明します。
1つ注意として、この真理条件は「文が真であることを示す証拠」とは区別されます。真理条件による意味理論の下では、「文の意味を知っている」ということは「その文が真となる条件を知っている」ことであって、「その文が真であるかどうかを判定する方法を知っている」ことではない、というわけです。この違いについては後できちんと触れることになるでしょう。
さて、この真理条件による意味理論は、意味の事実をかなりの程度説明できます。例えば、
- 同義性: 2つの文が同じ意味であるのは、その2つの文が同一の条件の下で真になるときである。
- 曖昧性: 文が同一の条件の下で真でも偽でもありえるが、矛盾はしないとき。
- 含意関係: $S_1$から$S_2$が帰結するのは、$S_1$が真だが$S_2$が偽であるということがありえないときである。
といった具合です。
意味=真理条件というアイデアの概要はこれで紹介できたと思います。ところで、このとき気になってくるのは、この「真である」とは一体どういうことなんだ、ということです。この問いに答えるためには、真理(truth)について考えなければなりません。なんだかヤバそうな感じになってきましたね。しかし安心してください。複雑な哲学的概念を使わなくとも、真理について語ることができるのです。
真理
タルスキ(Alfred Tarski)という哲学者は、真理というものを「真理述語」の定義によって分析しました。真理述語というのは「…は真である」という述語です。真理は「…は犬である」と同様、文の性質だというわけです。そして、このような真理述語は、以下のようなT-文(T-sentence)という形式で定義されるとしました。
$S$が真である iff $P$である
「iff」というのは、「―であるとき、かつそのときに限る」ということです。真理ってこれでもう説明できてるんじゃないの?というわけです。
この議論を自然言語の意味理論に利用したのがデイヴィドソン(Donald Davidson)です。上のT-文が真理述語を定義するのであれば、これは「真理条件」を表現していることになるでしょう。ですから、意味=真理条件とする立場は、このようなT-文を対象言語の各文$S$について構成するような言語理論を考えればよい、となるわけです。
合成性
では、T-文のような真理定義をどのように構成すればよいのでしょうか?ここでポイントになるのは、「私たちは見たこともない文であっても理解できる」という意味の事実です。この事実は、言い換えると「私たちは潜在的に無限の文を理解できる」ということになります。しかし、私たちには限られた経験と有限の語彙しかありません。この2つを整合的に理解するために持ち出される概念が、合成性(compositionality)です。
合成性の原理は、一般に以下のように説明されます。
文の意味は、それを構成する部分の意味の関数である。
もう少し平易に言えば、文の意味はそれを構成するパーツ(語)の意味で決まるよ、ということです。例えば「雪は白い」という文の意味は、「雪」という名詞の意味と、「白い」という述語の意味から決まるわけです。すなわち、私たちは文を細かいパーツに分解して、そのパーツに対する理解を「合成」することで文全体も理解できる、ということです。
これは、「私たちは潜在的に無限の文を理解できる」という事実に対する有力な仮説です。例えば、「雪」「草」「空」という名詞と「白い」「緑だ」という述語から、
- 雪は白い
- 草は緑だ
- 雪と草は白い
- 雪と空は白い、かつ、草は緑だ
...
という具合にいくらでも文を作ることができますが、合成的に考えればこの意味を私たちが理解できるのは自明でしょう。真理条件による意味理論は、このような合成性の原理に基づいて、複雑な文の意味(=真理条件)を説明しようとします。
真理条件からモデルへ
ここまでくると、通常の古典述語論理の意味論という感じがしてきます!いったんこれまでの話を整理しましょう。
- 真理条件による意味理論では、文の意味は真理条件として説明されます。
- 真理条件は、「〇〇が真であるのは、―のとき、かつその時に限る」というT-文によって明確化されます。
- T-文のような定義は、文の意味を合成的に捉えることによって与えることができます。
- このとき、合成的な意味論では、語の意味は指示対象・述語の意味は対象の集合になります。
まさにこのような考え方から、モデルによって意味を説明する「モデル論的意味論」が帰結するわけです。
さて、こうなると、結局真理条件による意味理論は意味の指示説の批判を免れていないのではないか?という疑問がわいてきます。しかし、いろいろな人が頑張って応答をしており、そしてそれは割とうまくいっています。例を見てみましょう。
例えば上に挙げた「指示対象が存在しない語」の問題については、ラッセル(Bertrand Russel)という哲学者による有名な議論があります。詳細には立ち入りませんが、ラッセルは"the ..."という確定記述(definite description)を主語とするような文は、一見するとその主語が人や物を指示対象にしているように見えるが、実はそれは見せかけにすぎないと主張します。そして、確定記述を主語とする文を「真理条件が等しいような別の文」に書き換える手続きを与えました。例えば、「『吾輩は猫である』の著者は日本人だ(the author of ... is Japanese)」は以下のように書き換えられます。
- 『吾輩は猫である』の著者が少なくとも一人いる ($\exists x.A(x)$)
- 『吾輩は猫である』の著者は高々一人である ($\forall x.(A(x)\to\forall y.(A(x)\to x=y))$)
- 『吾輩は猫である』の著者は、それが誰であれ日本人である ($\forall x.(A(x)\to J(x))$)
これを用いると、「現在のフランス国王(the present king of France)」のような確定記述が何か現実の対象を指示している、ということを前提にせずに済みます。そしてこの理論は、"the"を含む文の意味に関する様々な現象を説明できることが分かっています。
"the"に対する指示対象が明確ではないという問題も、このラッセルの確定記述に関する理論を使って解消できます。モンタギュー文法(Montague grammar)という理論では、"the"という冠詞に以下のような「翻訳」を割り当てることができます。そしてこの翻訳に対する指示対象を、高階型理論の意味論を用いて与えることができます。
$$
\texttt{the}\mapsto\lambda Y\lambda X\exists x(\forall y({}^{\lor} Y(x)\leftrightarrow x=y)\land{}^{\lor} X(x))
$$
なお、このように自然言語の意味を形式論理学の道具立てを使って研究する分野を、形式意味論(formal semantics)といいます(詳しくは[Gamut 1990])。
ちょっと脱線してしまいましたが、要約すれば、真理条件による意味理論は素朴な意味の指示説への反論の多くを乗り越えており、かつ様々な意味に関する現象を説明する能力がある、ということです。
批判
さて、このように真理条件による意味理論はかなり説明能力が高く、じっさい多くの支持者がいます。しかし、ここではあえて逆張りの立場をとって、それに反論してみようというわけです。そしてその反論は、最初に説明した意味の使用説に基づいてなされます。
意味の使用説を基本テーゼとしてしまった以上、真理条件による意味理論は棄却されたようなものではないかという気がしてくるかもしれません。しかし、2つの立場が両立すること、すなわち「意味が使用であるというスローガンに従いつつ、意味を真理条件により説明するような理論」の可能性があるかもしれません。そうではないよということは、何らかの形で論証する必要があるわけです。では見ていきましょう。
実効的に決定不能
まず、真理条件というのは「その文が真である条件」でした。このとき、真理条件を知っていることと、「その文が実際に真であると確かめる手段を持っていること」は違います。なぜなら、真であると確かめる方法がない文があるからです。いくつかの例を考えてみましょう。
サッカーを一度もせずに死んでしまった過去の人Aさんについて考えます。Aさんにサッカーの才能があったか・なかったかを私たちが確かめるすべはもうありません。なお、このような事柄の真偽が、私たちの認識に関係なく決まっているとする立場を実在論(realism)といいます。
私たちの普段使う言葉の中には、標準的な小学校レベルの算数は含まれていると想定してよいでしょう。すなわち、私たちの言語は算術(arithmetic)の言語を含んでいます。しかし、ゲーデルの不完全性定理から、(ざっくり言うと)このような言語の中には真であるとも偽であるとも証明できない文が含まれています。
このような言明は、実効的に決定不能(effectively undecidable)といわれます。そして、実効的に決定不能な文があるということは、真理というものは私たちの「認識手段」によっては到達できないことがあるということです。このようなことを真理の検証超越性(verification-transcendence)と言ったりします。真理条件による意味理論に対する批判は、このような真理と認識の関係に焦点を当てます。
表出論証・習得論証
さて、真理条件による意味理論へのダメットの批判は本当にたくさんあるのですが、その中でも有名な2つ「表出論証(manifestation argument)」と「習得論証(acquisition argument)」を紹介します。それらはどちらも、先ほど説明した意味の使用説に基づいて批判を行います。非常に粗いスケッチを描く程度の説明にはなってしまいますが、見ていきましょう。
一つ目の反論は、私たちの観察可能な行動に着目します。まず、言葉の意味を知っていることは、どのような能力でしょうか?例えば「「独身」とは「結婚していないことだ」という風に明示的に言い換える能力だ」とすることもできるかもしれませんが、これでは「言い換え」にキリがなくなってしまいます(無限後退)。ですから、私たちの言葉の意味に関する知識は、どこかの段階で「言い換えによる説明がつかない」、すなわち暗黙的です。となると、ある言葉の意味を知っている人とそうでない人を区別できるためには、実際にその言葉を使えるかどうかの違いが表にあらわれなければならないはずです。すなわち、意味の知識は振る舞いに表出(manifest)されます。
一方で、真理条件による意味理論は、実効的に決定不能な文の意味であっても真理条件によって説明してしまいます。しかし、実効的に決定不能な文については、(定義より)私たちがその真偽を認識することはできません。これを上の「表出」の要請と併せると、真偽を認識できないような真理条件に関する知識が、私たちの実際の振る舞いに表れることになってしまいます。このようなことはありえません。
二つ目の反論は、私たちが言葉を習得する(acquire)側面に着目します。意味の使用説の観点からすれば、私たちが言葉の意味を学ぶときに習得するのは、その使い方です。そして逆に、それ以上の何かが学ばれるとするのはおかしいでしょう。というのも、もしこのように考えれば、「ある人が直接教えられた使い方を習得し、周りの人と同じように振舞うが、しかしその人は実際はその言葉を理解していない」というケースがありえることになるからです。これでは言葉の意味というものが原理的には伝達不可能な、「私的な」ものになってしまいます。言葉というのは公共的なものですから、このようなことはありえない、というわけです。
さて、真理条件による意味の理論を仮定すれば、私たちが言葉を習得する際に学ぶのはその真理条件に関する知識です。しかし、実効的に決定不能な文の真理条件を私たちが学ぶというのはどういうことでしょうか?仮にそういったものを学ぶとすると、実効的に決定不能なわけですから、私たちはその真偽を認識できないわけです。認識できないということは、振る舞いには現れようがありません。すなわち、使い方以外の何かが学ばれていることになってしまいます。これはおかしいです。
以上が真理条件による意味理論への批判の大筋です。本当に本当に簡単にまとめてしまえば、真理というのは必ずしも我々には認識できないのだから、真理条件によって言葉の意味の知識・学習を説明すると、言葉の意味をその使い方として説明できなくなってしまう(使い方以上の何かを求めることになってしまう)という風に総括できると思います。
少し補足しておくと、私たちには実効的に決定不能な文が理解できない、とダメットは言っているわけではありません。真であることが確かめられない文が無意味であるとも言っていません(このような主張は、20世紀初頭の論理実証主義にみられるものです)。あくまで、私たちが色々な文の意味を理解ないし習得していることは所与の事実であり、真理条件による意味理論ではその事実が説明ができない、という批判の流れであることに注意しましょう。
真理から検証へ
ということで、意味の使用説をもとに、真理条件による意味理論が棄却されました(いろいろ反論はあるかもしれませんが、いったんそういうことにしておきましょう!)。
では、代替案となるような意味理論はどのようなものになるでしょうか?孫引きになってしまいますが、大西[2012]からダメットを引用します。
数学の言語の何らかの部分を学ぶとき、われわれがじっさいに学ぶのは、それぞれの言明について、何がその真理あるいは虚偽を確立すると見なされるのかを認識することである。非常に単純な言明の場合には、われわれはその真偽を決定する何らかの計算手続きを学ぶ。より複合的な言明については、何がその言明の証明あるいは反証と見なされるかを認識することを学ぶ。…それゆえわれわれは、真理の概念に代えて証明の概念を、数学的な言明の意味の理論の中心概念として据えねばならない。ある言明の意味の把握は、その証明が提示されたときにそれを証明として認識する能力に存する…。(Dummett, 1975a, 225)
この論文では数学の話をしているので「証明」とされていますが、これを自然言語一般に拡張するならば、意味理論の中心概念は検証(verification)ということになります。すなわち、言葉の意味をその検証手段によって特徴づけよう、というわけです。再度引用します。
そのような見解においては、ある言明の意味を知るとは、何がその言明を検証するものと見なされるか、すなわち、何がその真理を決定的に確立するものと見なされるかを認識する能力をもつことである(Dummett, 1975a, 227)
以上のような、真理条件による意味理論に対するダメットの批判は「ネガティヴ・プログラム」と言われます(批判しているだけなので)。ここで気になってくるのは、じゃあ検証に基づく意味理論って具体的にどういう形をとるのか?それで推論規則についての説明はできるのか?ということです。これ以降見ていくのは、その問いに答える「ポジティブ・プログラム」、すなわち、検証を中心概念とした意味論の構築と、それによる推論規則の正当化・批判のプロセスになります。
推論主義
「真理」から「検証」へ、と突然言われても理解しにくいと思うので、検証主義的な意味理論の立場をもう少し明確にしましょう。まず、ここまでの議論をもとにすると、今回の意味理論に要求されているのは以下の2つです。
- 意味の使用説: 意味をその使い方として説明する
- 検証主義的な意味理論: 文の意味の理解を、何がその検証(証明)になるかの基準の理解として説明する
これを具現化した立場として、本稿では推論主義(inferentialism)というものを導入します。推論主義の主張は、「言葉の意味とは、それが推論の中で果たす役割によって決まる」ということです。ぱっと見ると突拍子もないことを言っているように思えますが、これまでの主張をもとにすればそこまで変でないように思われます。すなわち、
- 推論というのは、私たちが言葉を使って行う活動です。よって、言葉の意味を、(ある特定の種類の)使い方に基づいて説明することになっています。
- 検証ないし証明は、推論によって行われます。よって、推論における言葉の役割を理解しているならば、その言葉による検証の是非も理解できるでしょう。
さて、この推論主義は自然言語一般に対して適用される話ですが(最近ではブランダムという人の議論が有名です)、今回は論理結合子の話しかしていません。そして、論理結合子の「推論における使い方」とは「推論規則」のことだと言ってしまってよいでしょう(論理結合子とは何のことなのかという問いが別でありますが、今回は最初に導入した$\land,\lor,\to,\bot~(,\lnot)$のことと思って話を進めます)。よって、推論主義の主張を論理結合子に限定したものは
論理結合子の意味は、推論規則によって定まる
となります。これを、これ以降の議論の基本方針にしたいと思います。
はい、ちょっと最後の方は駆け足になってしまいました(当日に急いで書いたので(汗))。繰り返しになりますが、何か変なところや私が誤解していそうなところがあれば、どんどんご指摘をいただきたいです。
さて、実はまだstep 1しか終わっていないんですね!議論としては準備段階が終わったくらいです。後編では、証明論的意味論の構築・古典論理の批判というメインテーマに移っていく予定です。お楽しみに。
