大学数学基礎解説

文献あり

哲学的視点からの直観主義論理入門 [後編]

論理学,直観主義論理,証明論的意味論

1279

こちらは ISer Advent Calendar 2021 24日目の記事です。長いので2つに別れていて、このページは後編です。前編はこちらです。

前編のあらすじ

前編の段階でかなりの長さになってしまったので、いったん話を整理します。

まず出発点は「なんで直観主義論理なんかを考えるのか？」というところでした。そこから「構成的な証明」という話をモチベーションにしつつ、「古典論理を批判して直観主義論理を擁護するためには、どのような議論がありうるか」ということを考え始めました。
そして議論のルートとして以下のようなものを考えました。
- 推論規則についての論争を、意味論によって解決する(=健全性定理を使う)
- 意味論についての論争を、自然言語の意味理論によって解決する

step	階層	批判対象	代替案
1	(自然言語の)意味理論	真理条件による意味理論	検証主義的な意味理論
2	(形式論理の)意味論	モデル論的意味論	証明論的意味論
3	推論規則	古典論理	直観主義論理

step 1として、自然言語の意味理論についての論争を紹介しました。
- 基本的なテーゼとして「言葉の意味とはその使用である」という意味の使用説を採用しました。
- 「真理条件による意味理論」を紹介し、それを意味の使用説に基づいて批判しました(表出論証・習得論証)。
- そして、意味理論の中心概念を「真理」ではなく「検証」にした検証主義的な意味理論を代替案として採用しました。そのアイディアを具現化したものとして、推論主義という立場を導入しました。

よって、これから明らかにしていかなければならないのは以下のポイントです。

検証主義的な意味理論(推論主義)を自然言語の意味理論のレベルで採用するとして、それは形式論理の体系に対する意味論のレベルではどのように実現されるでしょうか？
- この問いに対する答えとして、「証明論的意味論」というものを導入します(step 2)。
- ただし、これは素朴な推論主義ではうまくいきません。ちゃんとした意味論を作るためには、「調和」という一種の制約が必要になります。これをstep 2の前段階のstep 1.5で議論します。
証明論的意味論によって古典論理の批判や直観主義論理の擁護はどのようにできるでしょうか？
- この問いに対する答えは、前編で述べた通り健全性定理の成立・不成立によって説明されます(step 3)。

なお、後編の説明の大筋は[大西 2012]に従っていますが、各所の具体例や説明で大西先生のその他の文献や矢田部先生の解説などを参考にしています。詳しくは参考文献のリストを参照してください。

step 1.5. 調和

素朴な推論主義の欠陥

さて、「論理結合子の意味は推論規則で決まる」が、意味理論に関する議論から得られた方針でした。しかし、これだけではさすがに素朴すぎます。というのも、推論規則さえ作ってしまえば「なんでもあり」だからです。実際、変な推論規則を定義することで、めちゃくちゃな論理結合子を作れてしまいます。有名な例として $tonk$ というものがあります。

tonk

の推論規則

$\frac{A}{A tonk B} (tonk I), \frac{A tonk B}{B} (tonk E)$

導入則は $\lor$ と同じで、除去則は $\land$ と同じですから、規則の形自体に何か問題があるようには見えません。しかし、これを認めてしまうと、以下のように任意の論理式から任意の論理式を導出できてしまいます。

$\frac{\frac{A}{A tonk B}}{B}$

これにより任意の論理式が導出可能になってしまうという点で、 $tonk$ は体系全体を破壊します(これをテクニカルタームで「体系を自明化する(trivialize)」と言います)。このような状況は、さすがにブロックしなければなりません。というのも、演繹的推論に関する重要な事実として、「正しい」と「正しくない」の区別がなされる、ということがあるからです。「全部正しい」「なんでもok」では、正しいも何もあったもんではないということです(これは、直観主義論理と古典論理のどちらの立場をとるかに関わらず深刻な問題です)。

この例から分かるのは、「推論規則が意味を規定する」というときの「推論規則」には、何らかの制約が課されていなければならない、ということです。ではそれはどのような制約でしょうか？以下ではこの点について考えていきます。

複数の「使い方」の調和

本節のこれ以降の話は、「どうしてそう言えるか」の説明というより、「なぜそういう考えに至るか」の動機の説明に終始することをあらかじめ断っておきます(この記事は全体的にそういう感じですが、ここは特にその色が強いです)。

まず注目したいのが、推論という私たちの言語活動には、複数のやり方が存在する場合が往々にしてあるということです。以下のような例を考えてみましょう。

ケーニヒスベルクの橋の問題

特定の配置をした「橋」と「島」に対して、橋を1筆書きするような経路があるかという問題を考えます。これに対してオイラーがグラフ理論による解答を与えたというのは、離散数学などを勉強した方なら聞いたことがあるでしょう(全ての頂点の次数が偶数になることが必要十分条件です)。
さて、ここで一筆書きできないような橋と島の配置を考えます。このとき「Aさんが橋を全て渡った」という情報さえあれば、グラフ理論の定理として「Aさんはどこかの橋を2回渡った」ということが結論できます。一方でこのことは、別にグラフ理論を全く知らない人でも、「2回渡ったところを直接目で見て確かめる」という方法で結論することもできます。同じことを確かめる、2つの異なる検証方法があるということです。

複数の解法

大学受験数学なんかでは、綺麗な解法とそうでない解法がある場合があります。例えば、 $a_{n + 2} = a_{n + 1} + a_{n}$ で定まる数列(フィボナッチ数列)の100番目を求めろという問題に対して、おそらく望ましい解法は、特性方程式などを解いて一般項 $a_{n}$ を求めて、そこに $n = 100$ を代入することでしょう。一方で、愚直でパワープレイな解法として、 $a_{1}, a_{2}, \dots$ と1ステップずつ計算して $a_{100}$ にたどり着くというものも考えられます。このように1つの結論に至るための複数の解法(別解)があることがあります。

このとき、これら複数の推論の手法は、てんでバラバラであってよいわけではありません。グラフ理論と直接確認の結果は一致していなければおかしいですし、数学の答案で別解のそれぞれが違う結果を出していたらそれはもはや別解とはいえません。すなわち、複数の推論どうしが「食い違っていない」ことが必要になるということです。

これらの例だけから一般化するのはやや乱暴かもしれませんが、非常にざっくりとしたスローガンとして、推論の仕方(より一般化すれば言葉の使い方)が複数ある場合、それらは首尾一貫していなければならないということが言えそうです。言い換えれば、一つの方法が他の方法と(何らかの意味で)互いに噛み合わないような状況は批判されなければならない、ということです。このような言語の用法の間の整合性のことを、調和(harmony)といいます。

この概念は、言語の規範性というものを考えると飲み込みやすいかもしれません。推論や言葉の使い方には「正しい」「正しくない」の区別があり、どんなやり方も許容されるアナーキーではありません。このような正しさの線引きをもたらす原動力が、まさにこの調和に対する要請なんだという説明ができるかもしれません。

少し話題はそれますが、このような「調和」概念は、言語内において自己完結的に「正しさ」を議論するための道具立てといえるんじゃないかと思います。意味の指示説的な理論においては、言語の外側にある世界(e.g. 指示対象, モデル)との対応関係によって言葉の意味や推論の妥当性が決まったわけですが、今回のような検証主義的な意味理論のアプローチではそのような概念に頼りたくありません。そのため、「言葉と世界」ではなく「言葉と言葉」どうしの関係によって正しさを議論していこうという方向性にしたくなります。その「言葉と言葉」の関係のコアになるのが、使い方の整合性＝調和というわけです。

このような方向性で考えると、「言葉の使い方がその意味を定める」という基本方針は保ちつつ、「とはいえ言葉の使い方が調和していなければ批判されることになる(修正が必要になる)」と制約をつけくわえればよいのではないかという発想に至ります。そして裏を返せば、「調和が保たれていれば特に問題はない(正当化される)」ということにもなりそうです。

いったん話の流れを確認します。

step 1に基づき論理結合子の意味を推論規則によって規定しようとしていましたが、そこで $tonk$ という病的な例が現れ、このようなケースを除外しなければならなくなりました。
そして、対応策のベースとしてこの「調和」という制約を考えるところまで来ました。

しかし、「調和」と言われてもどのような整合性を考えればよいかはあまり明らかではなく、考察を進める足場としては心もとないです。よって、これからすべきことは、「調和」概念を論理結合子に関して定式化し、 $tonk$ が何らかの意味で「調和」を乱す、と説明することです。そしてその定式化は「反転原理」というものによって行われます。

反転原理と正当化

直接 vs 間接

繰り返しになりますが、「調和」とは言葉の複数の使い方に関する制約です。そして、論理結合子の使い方とは推論規則のことでした。では、推論規則が互いに整合的である・首尾一貫しているとはどういうことでしょうか？

ここで、上のケーニヒスベルクの橋の例を少し敷衍してみましょう。「Aさんはどこかの橋を2回渡った」( $A$ )ということを検証する方法には、実際に目で見て確かめるという「直接的」なものと、グラフ理論を使って確認するという「間接的」なものがありました。そしてこれらが食い違っていてはいけないという話でした。しかし、もう少し強いことが言えます。それは、これら2つが食い違っている場合、直されるべきは間接的な検証の方だ、ということです。すなわち、実際に確認したら2回渡っていないのに、グラフ理論による計算で2回渡ったことになってしまったのなら、「どうやら理論がおかしいぞ、修正しよう」となるはずだということです。

ここで「直接的」と雑に書いてしまった部分を明確にするなら、「その文の意味が分かっているのならばその文の検証方法がコレだと分かるものが直接的」と説明できます(「間接的」は直接的でないものです)。すなわち、 $A$ の意味を理解しているならば、「2回渡ったことを直接目で見て確かめる」が検証方法になっていることも理解できていなければなりません(これがまさにstep 1で検証主義的な意味理論の言わんとするところでした)。あるいはこの対偶を考えましょう: 2回渡ったことを直接見れば $A$ が検証できることが分からないなら、 $A$ の意味を分かっているとは言えそうにありません。そして、この直接的な検証手段に基づいて、間接的な検証手段が正当化・批判される、という関係にあることが分かります。

ここから、以下のような構図が見えてきます。

まず、言葉の意味を決定づける「直接的」と言えるような用法があり、その正しさは「そういうもの」として保障される(テクニカルタームで言えば自己正当化的(self-justifying))
そして、「間接的」な用法は、直接的な用法と「調和」することによって正当化される。

BHK解釈

では、論理結合子について「直接的」とはどういうことでしょうか。すなわち、「ある結合子の意味が分かっているなら、その結合子を含む論理式の検証(証明)を得る方法がこれだと分かっていなければならないような方法」とは何でしょうか？これを大まかに説明するものとして、論理結合子に対するBHK解釈(Brouwer–Heyting–Kolmogorov interpretation)というものがあります。これは、各論理結合子の証明をどのように構成するかを記述する非形式的な説明です。

BHK解釈

$A \land B$ の証明は、 $A$ の証明 $a$ と $B$ の証明 $b$ の組 $⟨ a, b ⟩$ である
$A \lor B$ の証明は、 $A$ の証明または $B$ の証明( $x$ とする)、そしてどちらの証明かを表す $i \in {0, 1}$ から成るペア $⟨ i, x ⟩$ である
$A \to B$ の証明は、 $A$ の証明 $a$ に対して $B$ の証明を返すような「関数」である
$⊥$ の証明は存在しない

このBHK解釈は、今回使っている自然演繹の体系NJでいえば「導入則」に相当します(カリー・ハワード同型対応をご存じの方なら、NJの導入則に対応する型付きλ計算の項の構成方法だと思ってくださればよいです)。すなわち、「ある結合子の意味が分かっているなら、その結合子の導入則が分かっているはずだ」ということが考えられているわけです。このような意味で導入則は「直接的」で「自己正当化的」です(もう少し意味をはっきりさせて意味付与的である(meaning-conferring)と言うこともあります)。今回はとりあえずこの主張を受け入れましょう。

では次に問題となるのは、導入則ではない「間接的な」推論規則の正しさがどのようにして議論されるか、ということです。ここからは、除去則に対して正当化の基準を定式化した「反転原理」というものを見ていきます。

反転原理: 導入則と除去則の調和

導入則と除去則の調和とは一体何でしょうか。まずはこれら2種類の推論規則を対比してみましょう。導入則は「その結合子を含む結論を何から導くか」、除去則は「その結合子を含む前提から何を導けるか」の記述になっています。ということは、除去則は導入則から見ればある意味で「逆」の操作です。すなわち除去則は、色々な根拠を組み上げて導出された論理式から、何らかの結論を引き出す操作だと言えます。このことは、「構成」と「解体」という対比によってよりクリアになります。導入則は、根拠から主張を組み上げて「構成」する操作です。反対に除去則は、組み上げられたものを「解体」して、何か帰結を取り出す操作だということです。

この対比から言えそうなことは、ある前提から結論として引き出せることは、それを組み上げてきた根拠以上に強くなってはいけないということ、簡単にいえば「根拠に対して結論が欲張ってはいけない」ということです。ある前提 $A$ を「解体」して結論 $B$ が出てきたとして、もし $B$ が $A$ を「構成」しているものと全然関係ないとしたら、それはなんだかミステリアスです。もっと言えば、私たちの推論という実践がまともなものだと言えるためには、「引き出せる結論(の正しさ)をその根拠(の正しさ)に還元できること」が必要なのではないかということです。ここが導入則・除去則の調和のキーになります。「結論」が「根拠」に対して見合わないような内容になっているとしたら、それは推論規則の調和の乱れに他ならないだろうと考えるわけです。

この「根拠に対して結論が欲張らない」という状況の定式化は、プラウィッツ(Dag Prawitz)によって以下の反転原理(inversion principle)として与えられました。

反転原理

$A$ を結論とするような結合子 $\circ$ の除去則( $α$ )を考える。このとき、この $α$ の前提のうち $\circ$ を含む論理式を導入則によって導くような証明図は、 $α$ の前提のうち $\circ$ を含まない論理式の証明図(そのようなものがある場合)と組み合わさったとき、すでに $A$ の証明図を「含んで」いる。このようにして、 $A$ の証明図を、所与の証明図に $α$ を追加せずに直接得ることができる。[Prawitz 1965をもとに改変]

ちょっとこれだけではよく分らないと思うので、個々の論理結合子で見ていきましょう。まず、一番簡単な $\land$ の除去則を考えます。 $\land$ の除去則が適用される状況は、一般に下図のように表せます。

そして、この前提のうち $\land$ を含む論理式が導入則によって導かれているような状況を考えると、次のようになります。

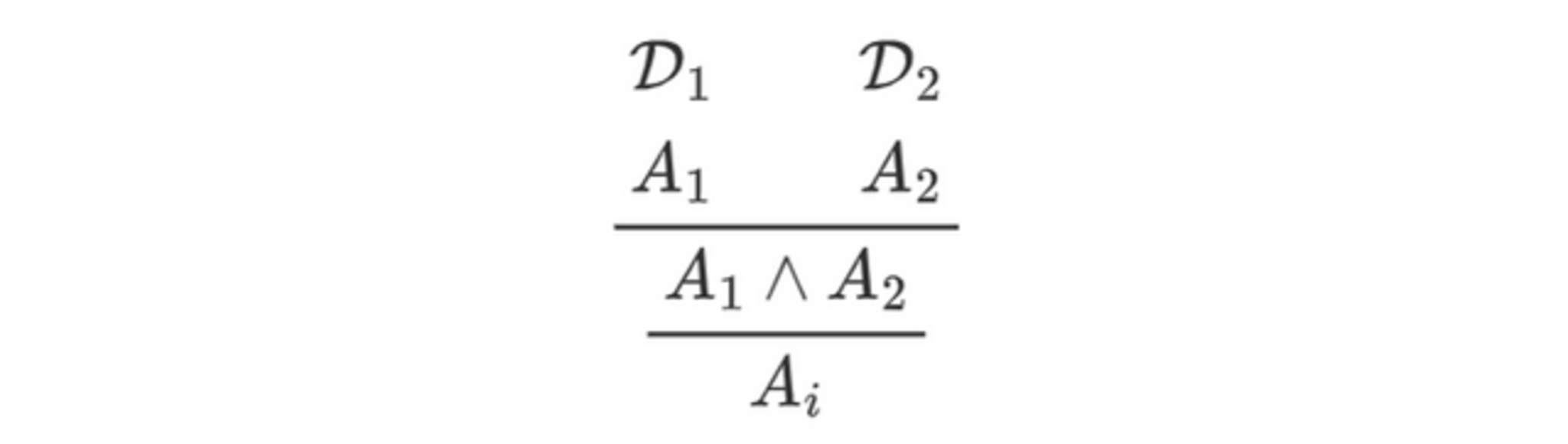
さて、この証明、なんだか無駄なことをしていないでしょうか？そう、 $A_{i} (i = 1, 2)$ は一番上の部分で既に証明されているのです。要は、証明に「遠回り(detour)」が含まれているということですね。このような、「導入則の直後に(同じ論理結合子に対する)除去則が適用されている箇所」を局所的ピーク(local peak)とよぶことにしましょう。そして、この局所的ピークは以下のように消去できます。

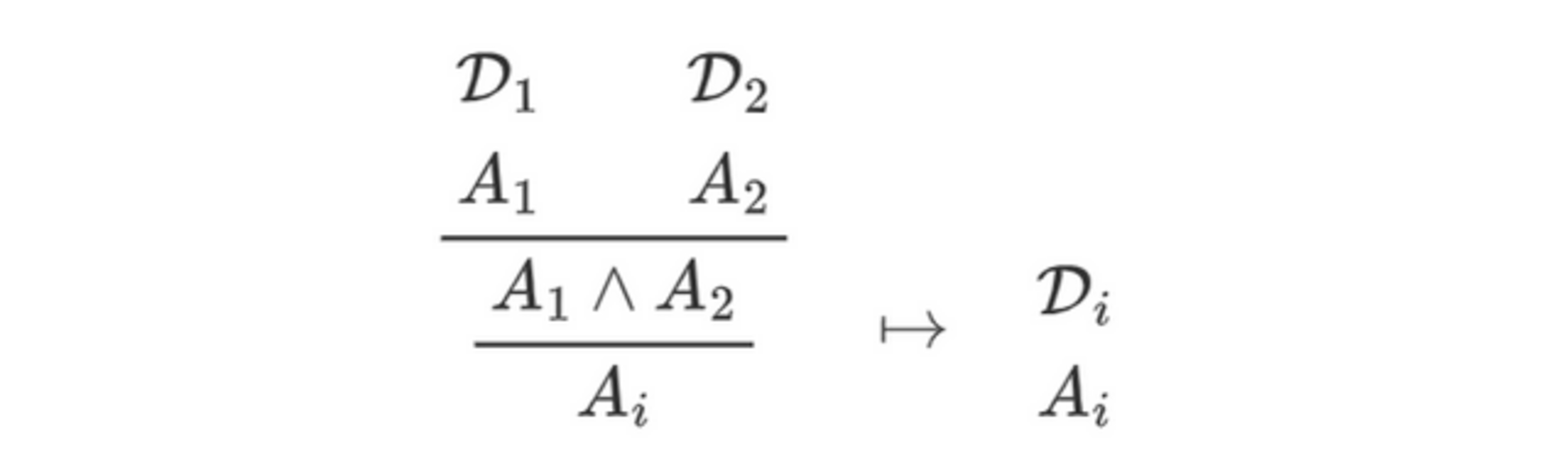
このような局所的ピーク消去の操作を簡約(reduction)と呼びます。反転原理が言っているのは、このような局所的ピークの簡約が可能であることだと言うこともできます。

その他の演算子に関する簡約も考えましょう。 $\lor$ については次のようになります。 $A_{i}$ を導出する部分( $D$ )と $A_{i}$ を仮定して $C$ を導く部分( $D_{i}$ )を「合体」させることで、「遠回り」をなくすことができています。

$\to$ については以下のようになります。 $\lor$ と同様ですね。

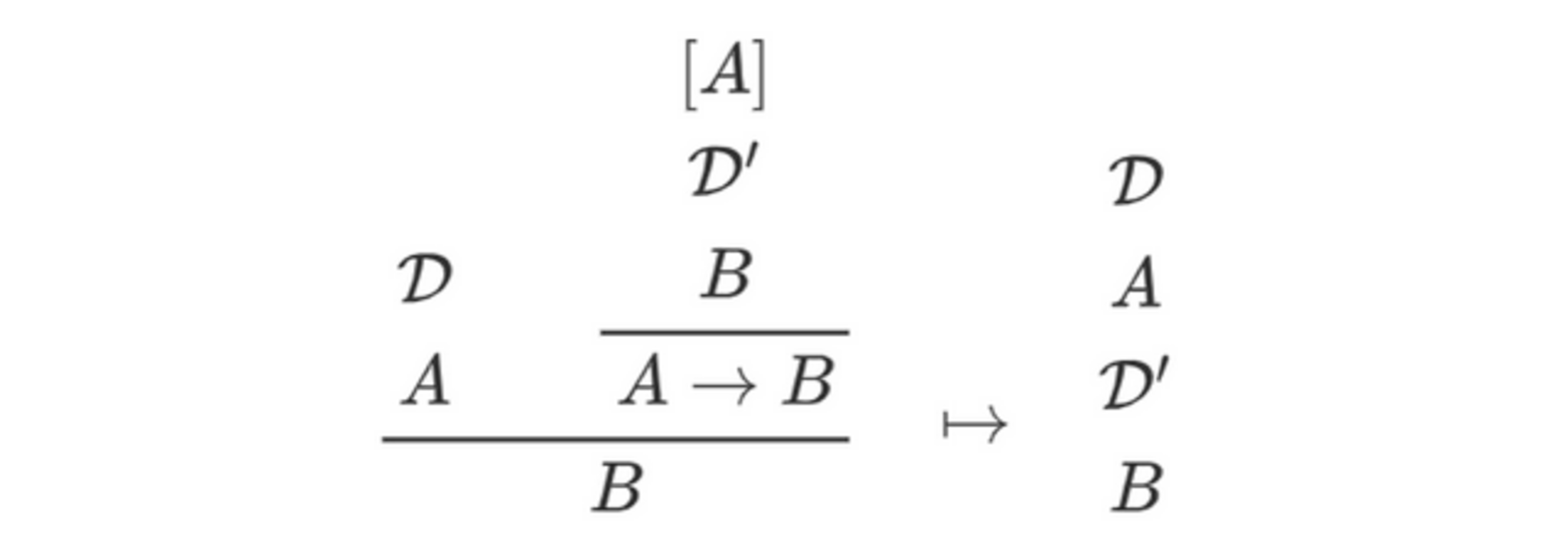
少しだけ補足をしておきます(よく分らなければ無視してください)。カリー・ハワード同型対応によれば、命題論理の論理式・証明図は、それぞれ型付きλ計算の型・項に対応します。そして、上で紹介した簡約は、型付きλ計算のβ簡約(beta reduction)に対応しています。例えば $\to$ の導入則・除去則はそれぞれλ抽象・関数適用に対応します。そして、上の簡約の操作は $[A]$ という自由変数に証明図(=項)を代入しているものと見なせます。すなわち、
$(λ x . D^{'}) D \mapsto_{β} D^{'} [x := D]$
のように表現することができます。

このような反転原理の観点からすれば、 $t o n k$ の推論規則が正当化されないことは明らかです。というのも、導入則の直後に除去則が来るような証明図を考えると、

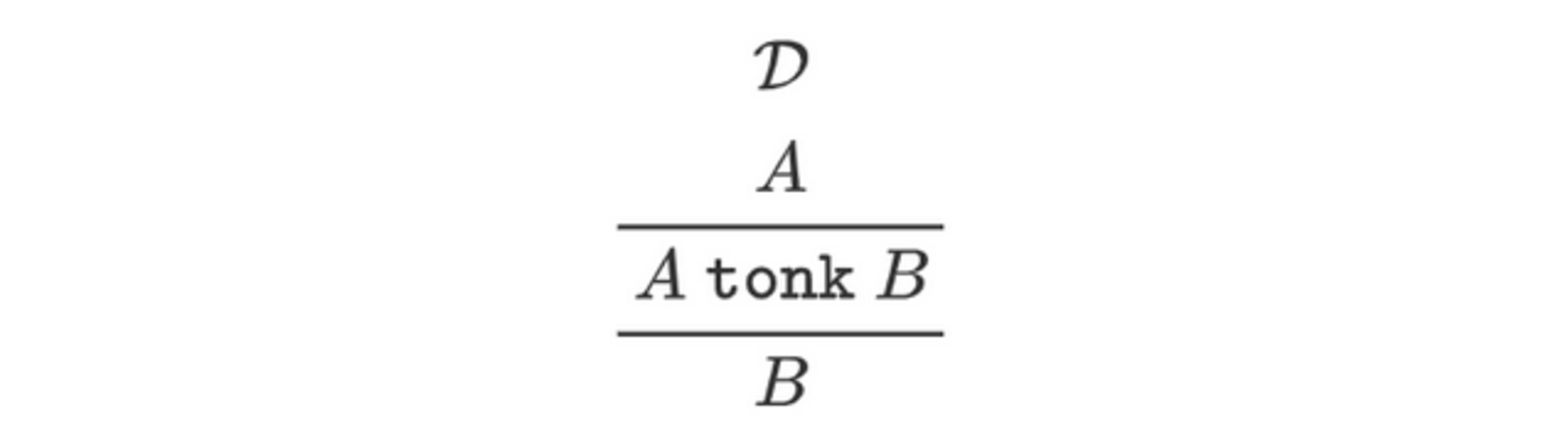
となりますが、 $A$ と $B$ が全く関係ない論理式にもなりうる以上、ここから局所的ピークがなくなるように簡約することはできそうにないからです(「できない」とはっきり示すだけの道具立てはまだ揃っていませんが)。このように $tonk$ の除去則は反転原理を満たさず、したがって調和という要請に反していることが分かります。このようにして、 $tonk$ のような病的な例をちゃんと排除することができました。

正規化定理

さて、上の簡約の操作を続けるといったいどうなるのか、という疑問がわいてきます。まず、これ以上簡約ができない証明図のことを正規(形)である(normal)ということにし、正規形にいたる有限の簡約ステップが存在する証明図を正規化可能である(normalizable)ということにしましょう。このとき、以下の定理が成り立ちます。

正規化定理 (normalization theorem)

NJの任意の証明図は正規化可能である。

ここから得られる系として、以下のものがあります。

部分論理式特性(subformula property)

開いた仮定の集合が $Γ$ であり、結論が $A$ であるようなNJの正規な証明図を $D$ とする。 $D$ に出現する任意の論理式 $B$ について、以下のいずれかが成り立つ。

$B$ は $A$ の部分論理式である
$B \in Γ$

部分論理式特性が成り立つために必要な簡約の操作として、実は上で各結合子について紹介したものだけでは不十分であり、いくつか例外的なケースに対する処理をするための簡約操作を付け足す必要があります(正規化定理はそのような簡約規則も込みで考えられています)。とはいえ、今回の議論の大筋には関係しないので割愛します。この点について詳しくは[矢田部 2017]を参照。

この性質は先ほどの「構成」と「解体」の観点からすると重要です。部分論理式特性が意味するのは、前提から結論を導くような証明は「不純物」(結論を導くために必要でなく、かつもとの前提にも含まれていないような論理式)が含まれていない形に変換できるということであり、これは論理的な推論に飛躍や誤魔化しが混じりこんでいないことに値します。このような観点から、「(部分論理式特性が成り立つような)正規化が可能であることは、記号体系が論理といえるための必須の条件である」と主張する人もいます。

さらに、NJの証明図に対して以下のようなよい性質が成り立ちます。これは、この後出て来る証明論的意味論とNJの関連を論じる上で重要です。

導入形式特性(introduction form property)

NJの任意の閉じた証明図は、最後に適用される推論規則が導入則になる形式に(有限ステップで)簡約可能である。

証明論的意味論へ

少しテクニカルな話が続きましたが、以上で「導入則と除去則の調和」「簡約により除去則を正当化する反転原理」という大枠をたどってきました。

しかし、これだけでは推論一般について語ることはできません。例えば、古典論理の排中律や二重否定除去則は、純粋な導入則・除去則ではありませんから、これまでの枠組みでは正しさを議論することができません。もっといえば、一般に推論規則というのは導入則か除去則の形をしている必要はありません。例えば、NKに以下の推論を「規則」として追加してもよいわけです(証明できることは増えませんが)。
$\frac{A \land B}{B \land A}$
というわけで、「除去則に限られない、(導入則以外の)様々な推論規則一般」の正当化について考えなければなりません。そしてそのためには、「簡約による正当化」という反転原理のアイデアを拡張して、除去則以外の推論についても議論できるようにしなければなりません。そこでいよいよ登場するのが、証明論的意味論です。

step 2. 証明論的意味論

冒頭で説明した議論の流れを思い出しましょう。意味の使用説を踏まえることで、(自然言語に関する)真理条件による意味理論によって支持されるモデル論的意味論は批判されます。そうなると、その代替案となるような(論理結合子に関する)意味論を作ることが必要になる、という話の流れでした。step 2で行うのはこの作業です。ここが後編の山になります。

今回は、step 1と1.5で紹介した「推論規則による意味の規定」と「反転原理」というアイデアを実現したものとして、証明論的意味論(proof-theoretic semantics)というものを(やや厳密さには欠けますが)導入していきます。ここでの目標は、帰結関係(consequence relation)、すなわち、「 $A_{1}, \dots, A_{n}$ から $B$ への推論は妥当である」( $A_{1}, \dots, A_{n} ⊨_{PTS} B$ )という関係を定義することです。定義には色々流派があるのですが(後述)、今回のものは[Schroeder-Heister 2006]および[Schroeder-Heister 2018]に基づいています。

なお、先によくある誤解を解いておくと、「証明論的意味論は証明によって妥当性を決める」というのは割とミスリーディングです。こういう言い方をすると「証明可能性( $⊢$ )と妥当性( $⊨$ )の何が違うの？」という感じがしてしまいます。確かに自然演繹の証明図のようなものを使って妥当性は定義されるんですが、むしろコアとなるのは証明図の書き換え操作(=簡約)による正当化です。このことをなんとなく念頭に置いておいてください。

まずは非形式的な導入、それから形式的定義、という順に話を進めます。

非形式的な導入

導出構造

証明論的意味論では、まず「論理式の導出」に対して妥当性が定義されます。ふつうのモデル論的意味論では「論理式」に対して妥当性が定義されることを考えると、ちょっと意外ですよね。しかし、step 1で述べた通り推論主義の立場では「推論」をベースに言葉の意味を捉えるので、ここが出発点になります。論理式レベルの妥当性は、導出に対する妥当性を基に後で定義します。

さて、ここでいう「導出」としては、いわゆる自然演繹の証明図というよりは、「正しい証明かどうかまだわかっていない証明の候補」が考えられています(だから妥当性を考えているわけですよね)。たとえば、以下のようなめちゃくちゃなものも考慮の対象です(これは最終的には妥当ではないとされることが期待される例です)。

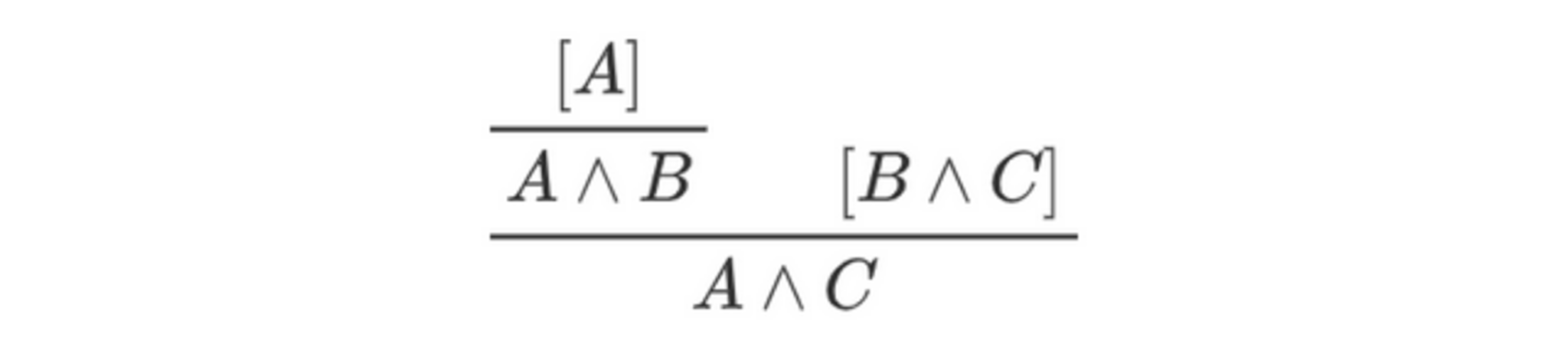
このような一般的な証明図の概念を導出構造(derivational structure)といいます(論証(argument)と呼ぶ文献もあります)。きちんと定義するならば、導出構造は「一般化された推論規則」を任意に組み合わせたものです。ここで、一般化された推論規則とは以下のようなものです。

0個以上の導出構造から1つの結論を導く
0個以上の仮定を解消(discharge)する

形式的には以下のように表現できます。

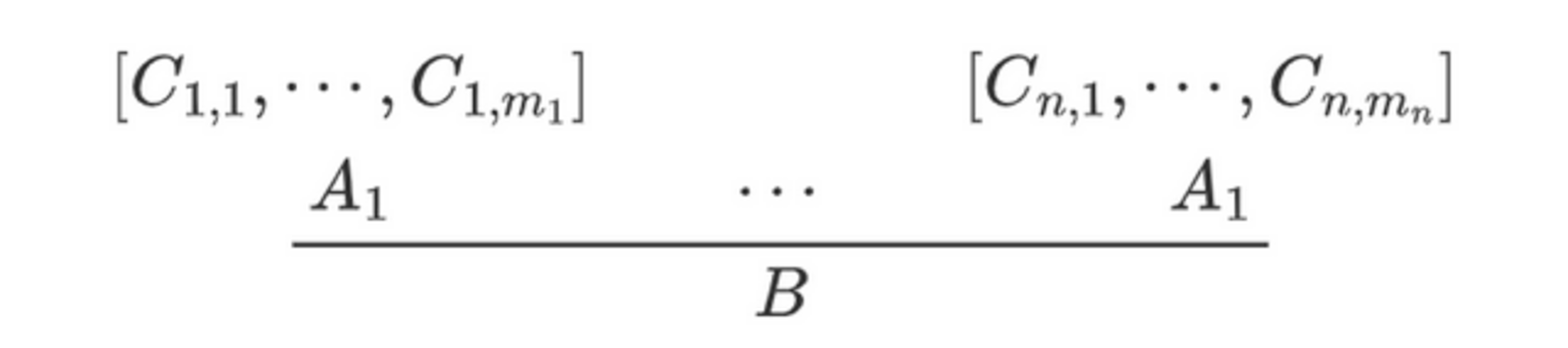
あるいは、以下のように仮定の部分をまとめると分かりやすいかもしれません。

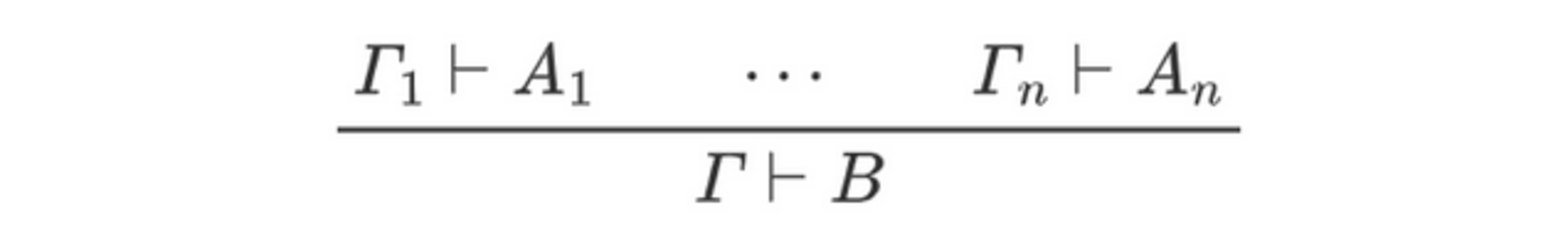
「組み合わせる」「解消する」といったインフォーマルな言葉遣いが引っかかる方もいると思いますが、今回は大目に見てください。また、本当は仮定の解消の際には番号を振ったりしてどの仮定が解消されるかを明確にしないといけないのですが、本稿では紛らわしくない限り省略します。

なお、導出構造は一般に $D$ のような書体で表します。また、結論部分が $A$ の場合は $D / A$ と書くことがあります。さらに証明木のスタイルで書くときには、解消されていない仮定や結論を明示して以下のように書くことがあります(3つとも同じものを表していて、単に書き方が違うだけです)。

導出構造の妥当性

先述の通り、まず導出構造に対して妥当性の概念が定義されます。そして、妥当性は導出構造の形式に関して場合分けして行われます。それぞれのケースの非形式的な説明を見ていきましょう。

カノニカルな導出構造と、その妥当性

step 1.5の反転原理のところで述べた通り、導入則は「自己正当化的」であり、除去則を含むその他の推論規則の正当化のベースになるような推論規則です。この構図は証明論的意味論でも変わりません。すなわち、導入則は正当化なしで「正しい」ものとして扱われます。このことを考慮して、前提を導く部分が妥当な導出構造であれば、それらに導入則をつけて新たな導出構造を構成しても妥当なままである、という風に定義します(これによって導入則の「自己正当化的」な性質を妥当性の定義に反映しようということです)。

「導入則をつけて～」という部分が今後大事になってくるので、以下のような性質を定義します。

カノニカル性

最後に適用されている推論規則が導入則であるような導出構造を、カノニカルである(canonical)という。

上の説明をこの言葉を使って言い換えれば、「カノニカルな導出構造は、仮定の論理式に対する導出構造が妥当ならば、全体として妥当」となります。

カノニカルではない導出構造の妥当性

step 1.5の反転原理のところで述べた通り、除去則を含む証明図は簡約の操作によって「正当化」されるのでした。これを導出構造に対しても拡張しましょう。すなわち、特定の形式の導出構造から別の導出構造への「書き換え」の操作を考え、カノニカルではない導出構造をこの書き換え手続きの有限回の適用で簡約することを考えます。このような一般の書き換え手続きを、以下のように定義しましょう。

正当化

導出構造から導出構造への書き換え規則であって、以下の条件を満たすものの集合を正当化(justification)という。

結論の論理式が同じ
開いた仮定を増やさない
代入について閉じている (開いた仮定の部分に導出構造を代入しても、書き換え可能性に影響しない)
など

正当化 $J$ によって導出構造 $D$ が $D^{'}$ に1ステップで簡約されることを、 $D \mapsto_{J} D^{'}$ と表し、これが0回以上の有限回の簡約の場合は $D \mapsto_{J}^{*} D^{'}$ と表す。

※定義の中で「など」と書いたのは、定義の流派による違いがありはっきりしたことが言えないからです。また、 $\mapsto_{J}$ は一般的な表記法ではなく、この記事で一時的に用いている略記です。また、「正当化」というのは一般名詞とやや紛らわしいかもしれませんが、文脈で分かると思います。

開いた導出構造の妥当性

さて、自然演繹では仮定が完全に解消されていないような演繹も許容されており、これを「開いた」証明図と言います。導出構造についても同様に「閉じた」「開いた」を考えることになります。これまで説明してきた2つのケースは、どちらも閉じた導出構造に対する定義になります。では開いた導出構造の妥当性は、どのように定義すればよいでしょうか？

ここで、解消されていない仮定を「自由変数」のようなものと見なしてみましょう。実際、仮定の部分に様々な証明図を「代入」「当てはめ」することで、例えば下図のように導出構造全体を閉じたものにすることができます( $p, q$ は公理か何かだと思ってください)。

そして、「仮定」というのは「それが正しかったら...」を考えるものであって、その正しさがどう導かれるかに関心を払うものではありません。ですから、このとき代入される導出構造に依存して妥当性が変化したら困ります。よって、開いた導出構造は、仮定の部分に 任意の 代入操作を行った結果によって正当化されることにします。

原子ベース

さて、ここまでの説明では命題変数が結論となる導出構造の妥当性がうまく扱えません(カノニカルな導出構造の結論は論理結合子を含んでいるからです)。これは、通常のモデル論的意味論と同様に対応することができます。すなわち、付値によって命題変数の真偽値を決めたのと同様、「どの命題変数がすでに証明されたと見なすか」を決めてしまえばよいのです。これを規定するものとして、以下のような概念を導入しましょう。

原子ベース

命題変数の間の推論規則の集合のことを、原子ベース(atomic basis)という。
なお、推論規則を持たない「空な」原子ベースを $S_{0}$ とする。

原子ベースの例

$S = {\frac{}{p}, \frac{}{q}, \frac{p q}{r}}$

モデル論的意味論で付値が「何が真か」を説明するのと同様、証明論的意味論では「何が証明できているか」を説明します。例えば $S_{0} (= \emptyset)$ は、どんな命題変数もまだ証明されたとはしない状況に相当します。また、[大西 2012]の脚注でちらっと挙げられている原子ベースの例は、四則演算に関する体系です(「 $a = b$ ならば $a + 1 = b + 1$ 」とかでしょうか？おそらく、それぞれの等式が各命題変数と対応していると考えているのではないかと思います)。

妥当性・帰結関係

ここまでで、証明論的妥当性の「気持ち」が説明できたんじゃないかと思います。ここから、妥当性を(ある程度)形式的に定義していきます。

原子ベース・正当化に基づく妥当性

(S, J)

-妥当性

原子ベース $S$ 、正当化 $J$ に対して、 $(S, J)$ -妥当な論証構造の集合を、以下を満たす最小の集合として帰納的に定義する。
ただし、 $S^{'} \supseteq S$ [resp. $J^{'} \supseteq J$ ]は、 $S^{'}$ [resp. $J^{'}$ ] が $S$ [resp. $J$ ]に規則を0個以上追加したものであることを表す(すなわち集合としての包含関係)。

$S$ の任意の閉じた導出構造 $D$ は、 $(S, J)$ -妥当である。
閉じたカノニカルな導出構造 $D$ が $(S, J)$ -妥当であるのは、 $D$ の直前の部分構造が全て $(S, J)$ -妥当であるときである。
- ただし、「直前の部分構造」(immediate substructure)とは、最後の(一般化された)推論規則の適用における仮定の導出構造を指します。
閉じたカノニカルではない導出構造 $D$ が $(S, J)$ -妥当であるのは、ある $(S, J)$ -妥当な導出構造 $D^{'}$ が存在して $D \mapsto_{J}^{*} D^{'}$ となるときである。
開いた導出構造 $D$ について、その解消されていない仮定を $A_{1}, \dots, A_{n}$ として、 $D$ が $(S, J)$ -妥当であるのは、任意の $S^{'} \supseteq S$ および $J^{'} \supseteq J$ 、そして任意の $(S^{'}, J^{'})$ -妥当な閉じた導出構造 $D_{1} / A_{1}, \dots, D_{n} / A_{n}$ に対して、以下の導出構造が $(S^{'}, J^{'})$ -妥当であるときである。

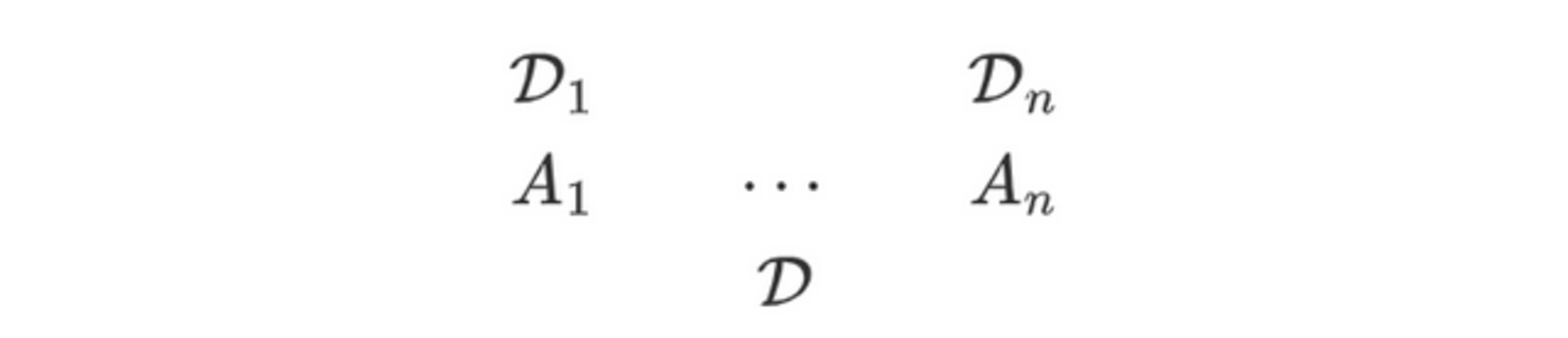
定義に関する補足

3は「簡約による除去則の正当化」の一般化と見なせます。このとき $\mapsto_{J}^{*}$ という簡約は非決定的である(non-deterministic)ということに注意してください。すなわち、どのような順番でどの規則が適用されるか分からないが、少なくともある「上手い」順番で書き換えれば妥当な導出構造になる、ということです。
4において、開いた仮定の部分に導出構造を「代入」するのは先ほど説明したとおりです。ここで、なぜ原子ベースや正当化を「拡張」したもの( $\supseteq$ )を考えているのかについて補足しておきます。
- とても素朴な理由として、これをしなければ望ましくない例が妥当になる、ということが挙げられます。例えば開いた仮定 $A$ を持つような導出構造 $D$ について、 $A$ を結論に持つ $(S, J)$ -妥当な導出構造が存在しない場合、 $D$ は空虚に(vacuously)条件4を満たします。たとえば $S$ が空な原子ベース $S_{0}$ であった場合はこのようなことは容易に起こりうるでしょう。だから任意の拡張を考えています。
- 厳密ではないがイメージしやすい説明もあります。それは、 $S$ や $J$ に新たな規則が追加されたとして、それによってもとの $S$ や $J$ について妥当だったものが妥当ではなくなったら困るだろう、ということです。
- もう一押し説明を加えておきます。 $S$ をある種の状態と見なし、 $S \leq S^{'}$ を状態から状態への遷移のような関係と見なしてみましょう。そうすると、4において拡張を考えているのは、直観主義論理のクリプキモデルにおける遺伝性(heredity)に類比的だと言えます。

単調性

妥当性の定義からすぐに言えることとして、 $S$ や $J$ を拡張しても妥当性は保存されるということがあります。すなわち、

単調性(monotonicity)

$D$ が $(S, J)$ -妥当かつ $S^{'} \supseteq S, J^{'} \supseteq J$ ならば、 $D$ は $(S^{'}, J^{'})$ -妥当である。

原子ベース・正当化によらない妥当性

さきほど定義した妥当性は、原子ベースと正当化に対して相対的な定義でした。モデル論的意味論の妥当性の定義では「任意の付値」を考えますから、それにならって原子ベースを任意にとることにしましょう。すなわち、

J

-妥当性

導出構造 $D$ が $J$ -妥当である $\overset{def}{\Leftrightarrow}$ 任意の原子ベース $S$ に対して、 $D$ が $(S, J)$ -妥当である

単調性より、以下のように $J$ -妥当性を特徴づけることも可能です。

導出構造 $D$ が $J$ -妥当である $iff$ $D$ が $(S_{0}, J)$ -妥当である

そして、正当化の手続きは少なくとも1つあればよいわけですから、 $S, J$ によらない妥当性は以下のように定義できます。

妥当性

導出構造 $D$ が妥当である $\overset{def}{\Leftrightarrow}$ ある正当化 $J$ が存在して、 $D$ が $J$ -妥当である

帰結関係

以上を踏まえて、目標であった帰結関係を考えましょう。すなわち、「 $A_{1}, \dots, A_{n}$ を前提としたとき、 $B$ を結論とするのは妥当である」という関係を定義します。これは、 $A_{1}, \dots, A_{n}$ から $B$ を導くような「1ステップの推論規則」を考えて、「仮定に対する妥当な導出構造をもとに、1ステップの推論規則で導出構造を作ると、その導出構造も妥当になる」というふうに定義します。

帰結関係

⊨_{PTS}

$A_{1}, \dots, A_{n} ⊨_{PTS} B \overset{def}{\Leftrightarrow}$ 任意の妥当な閉じた導出構造 $D_{1} / A_{1}, \dots, D_{n} / A_{n}$ に対して、以下の導出構造が妥当である

この定義は、非常に粗い言い方をすれば、「仮定に対する任意の妥当な導出構造に対して、結論に対する導出構造も妥当になる」となります。こう解釈すると、証明論的意味論における帰結関係 $⊨_{PTS}$ は、「仮定を充足する任意のモデルに対して、結論もそのモデルによって充足される」というモデル論的意味論における帰結関係によく似ています。「～を充足するモデル」を「～に対する妥当な導出構造」に置き換えたような感じですね。このことは、帰結関係において前提から結論へと保存されてほしい性質が「モデルによる充足」から「導出構造の妥当性」に移ったということを意味します。まさに、「「真理」から「検証」へ」というstep 1の方向性を実現した定義になっているわけですね。

帰結関係の例

さすがにこれだけだと「ちょっと何言ってるのか分からん」という感じかもしれないので、一つ例を見てみましょう。やることとしては、(相互)再帰的に記述された妥当性の定義を順番にたどっていくだけです。ただ、中身の薄さのわりに長くて退屈なので、よく分らなければ(あるいは読む気が起きなければ)飛ばして先に進んでください。加えてもう一点、定義をもとに自分で書いた証明であって文献から引いたものではないので、正直自信がありません。間違いを見つけた方はコメント欄で教えていただけると幸いです。

任意の $A, B, C \in Fml$ に対して、 $A \to B, B \to C ⊨_{PTS} A \to C$

任意の妥当な閉じた導出構造 $D_{1} / A \to B, D_{2} / B \to C$ をとり、以下の導出構造 $D$ が妥当であることを示します。

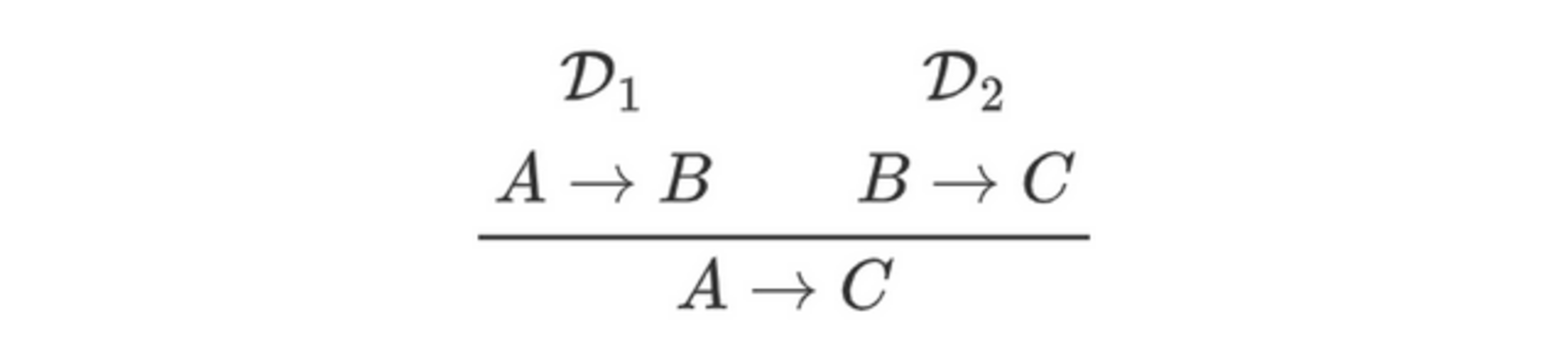
$D_{1}$ は妥当なので、ある正当化 $J_{1}$ が存在して $D_{1}$ は $(S_{0}, J_{1})$ -妥当です ( $J$ -妥当性は $(S_{0}, J)$ -妥当性によって特徴づけられたことを思い出しましょう)。ここで、 $D_{1}$ は閉じていて結論が複合式なので、定義7の項2または3に該当します。いずれにせよ、 $D_{1} \mapsto_{J}^{*} D_{1}^{'}$ となる $(S_{0}, J_{1})$ -妥当で閉じたカノニカルな導出構造 $D_{1}^{'}$ が存在します (「いずれにせよ」というのは、2に該当する場合(カノニカルな場合)は $D_{1}^{'} = D_{1}$ であり、3に該当する場合(カノニカルでない場合)は1回以上の簡約を経て $D_{1}$ が $D_{1}^{'}$ になるということです)。そして、 $D_{1}^{'}$ はカノニカルなので、定義7の項2に該当します。よって、直前の部分構造 $D_{1}^{″}$ もまた $(S_{0}, J_{1})$ -妥当になります。

$D_{2}$ に対しても同様の議論が成り立ち、上と同様のことが成り立つような正当化 $J_{2}$ および $(S_{0}, J_{2})$ -妥当な導出構造 $D_{2}^{″}$ が存在します( $A, B$ がそれぞれ $B, C$ になるだけ)。

このとき、 $J_{1} \cup J_{2}$ に以下を規則として追加したものを $J$ とします (ここで、 $D_{1}, D_{2}$ は任意の導出構造をとるメタ変数であり、 $A, B, C$ は任意の論理式をとるメタ変数であることに注意)。

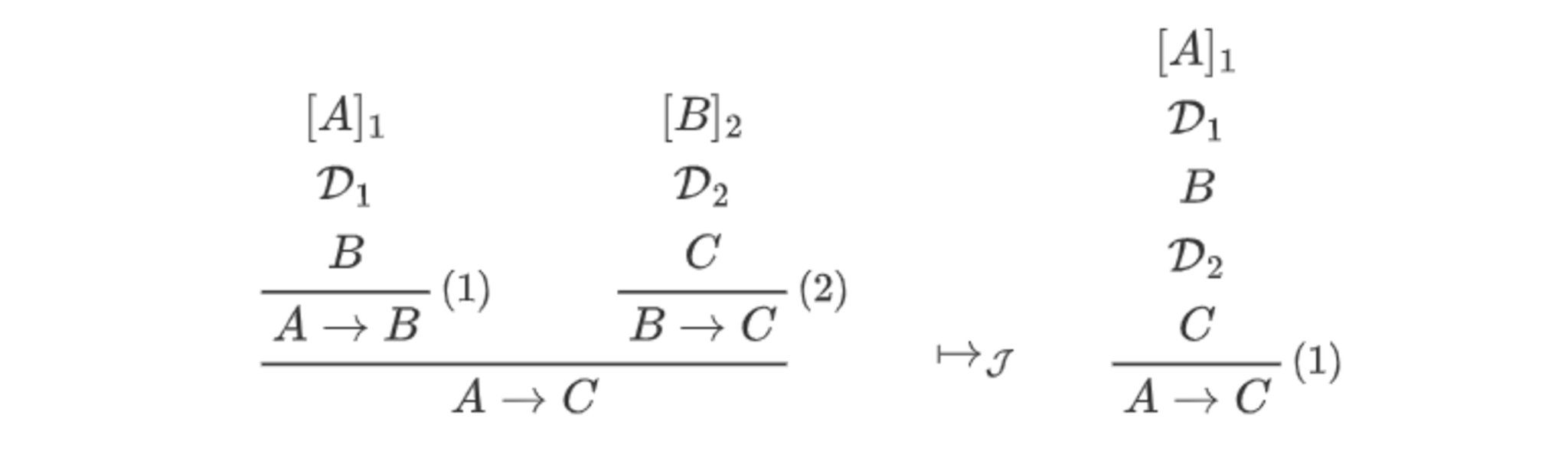
$D$ が $(S_{0}, J)$ -妥当であることを示せば、例の帰結関係を示したことになります。

まず、 $J$ の定義より、以下のような簡約ステップが構成できます。

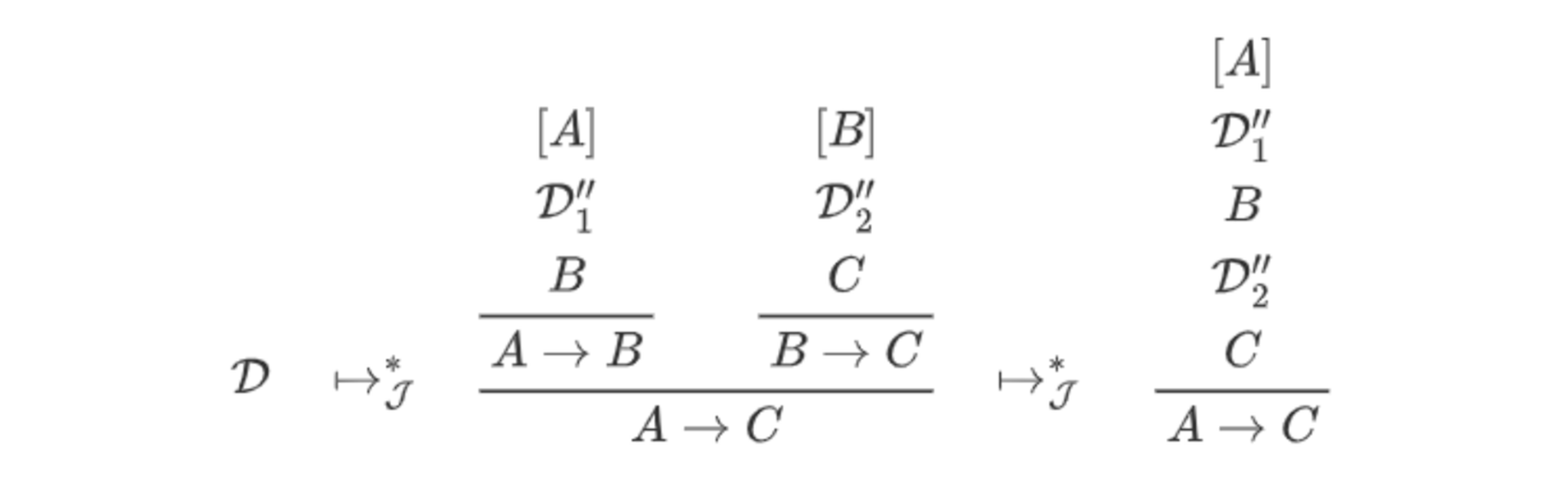
$D$ は閉じていてカノニカルではないので、定義7の項3に該当します。よって、この最右辺の導出構造を $D^{'}$ として、 $D^{'}$ が $(S_{0}, J)$ -妥当であることを示せば十分です。そして、 $D^{'}$ は閉じていてカノニカルなので、定義7の項2に該当します。よって、 $D^{'}$ の直前の部分構造を $D^{″}$ として、 $D^{″}$ が $(S_{0}, J)$ -妥当であることを示せば十分です。

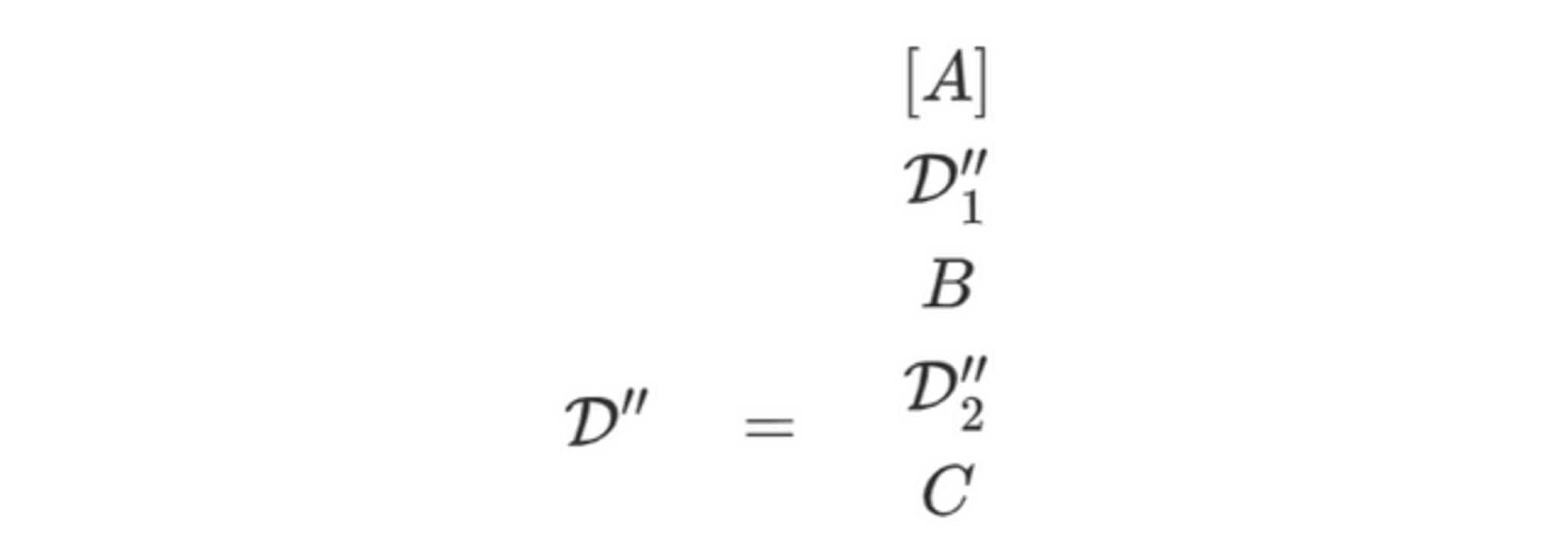
$D^{″}$ は開いた導出構造なので、定義7の項4に該当します。よって、任意の $S^{'} \supseteq S_{0}, J^{'} \supseteq J$ 、および $(S^{'}, J^{'})$ -妥当な閉じた導出構造 $D_{a} / A$ をとり、以下の導出構造 $D^{‴}$ が $(S^{'}, J^{'})$ -妥当であることを示せば十分です。

ここで、 $D_{1}^{″}, D_{2}^{″}$ はそれぞれ $(S_{0}, J_{1})$ -妥当, $(S_{0}, J_{2})$ -妥当でしたから、単調性よりどちらも $(S^{'}, J^{'})$ -妥当です。このとき、 $D_{1}^{″}$ は $(S^{'}, J^{'})$ -妥当な開いた導出構造なので、定義7の項4に該当します( $[A]$ の部分に「代入」をしても妥当性が保存)。よって、 $D_{a}$ の $(S^{'}, J^{'})$ -妥当性と併せて、以下の導出構造 $D^{⁗}$ が $(S^{'}, J^{'})$ -妥当になります。

$D_{2}^{″}$ も同様に $(S^{'}, J^{'})$ -妥当な開いた導出構造なので( $[B]$ の部分に「代入」をしても妥当性が保存)、 $D^{⁗}$ の $(S^{'}, J^{'})$ -妥当性と併せて、 $D^{‴}$ は $(S^{'}, J^{'})$ -妥当になります。

以上により、 $A \to B, B \to C ⊨_{PTS} A \to C$ が成り立ちます。 $◻$

以上の長ったらしい証明のコアになるのは、以下の2つの手続きです。

仮定の論理式に対する導出構造は妥当だとしているので、カノニカルな導出構造に書き換えられる
仮定の論理式に対する導出構造を全てカノニカルにしたら、導出構造全体を適切に書き換える規則を適用する(そのような規則は事前に作っておかなければならない)

余談ですが、これはなんとなく、プログラミングでいう「値呼び(call-by-value)」の評価戦略に似ているような気がします。仮定の導出構造は全体の導出構造からすればある意味で「引数」になっていて、それらを全て計算(=カノニカルなものに書き換え)してから、全体を計算しているわけですね。とすると、「導出構造の妥当性 = 評価が停止するような計算手続きをうまく与えられること」といった見方もできるかもしれないと思いました(だからなんだという話ではありますが)。

step 3. 古典論理の推論規則への批判

ここまでで、前編・後編にわたり、検証主義的な意味理論(推論主義)→証明論的意味論、と話を進めてきて、やっと推論規則のレベルに戻ってきました。これからすべきことは、証明論的意味論を用いて直観主義論理を擁護し、古典論理を批判することです。そしてそれは、冒頭で述べた通り、健全性定理を用いてなされます。

NJの正当化

まず、証明論的意味論をもとに、NJの推論規則に問題がないことを確認しましょう。

NJの健全性

証明論的意味論に対してNJは健全である。すなわち、任意の有限集合 $Γ \subseteq Fml$ および $A \in Fml$ に対して、 $Γ ⊢_{NJ} A$ ならば $Γ ⊨_{PTS} A$

反転原理のところでほとんど説明は済んでいるので、証明の概略だけ説明します。

証明は証明図の構成に関する帰納法によります。すなわち、それぞれの推論規則が帰結関係になっていることを示します(例えば $\land$ の導入則については $A, B ⊨_{PTS} A \land B$ を示します)。
以下では、NJの正規化定理(定理1)における簡約手続きを $J_{norm}$ とします。

導入則

: 仮定の論理式に対する妥当な閉じた導出構造を任意にとったとき、これらを導入則で組み合わせたものは閉じたカノニカルな導出構造ですから、定義7の項2より明らかに妥当です。よって導入則は帰結関係になっています。

除去則

: まず $\to$ について説明します(実は内容はstep 2の最後の例とほとんど同じなので、要所しか書いていません。詳細が気になる方はstep 2の最後の例を読んでみてください)。
妥当な閉じた導出構造 $D_{1} / A, D_{2} / A \to B$ を任意にとったとき、これらを $\to$ の除去則で組み合わせた導出構造 $D$ を考えます。 $D_{1}, D_{2}$ はそれぞれ妥当な閉じた論証なので、(ある正当化が存在して)カノニカルな導出構造に変換できます。よって、 $D$ 全体を以下のように変換できます。

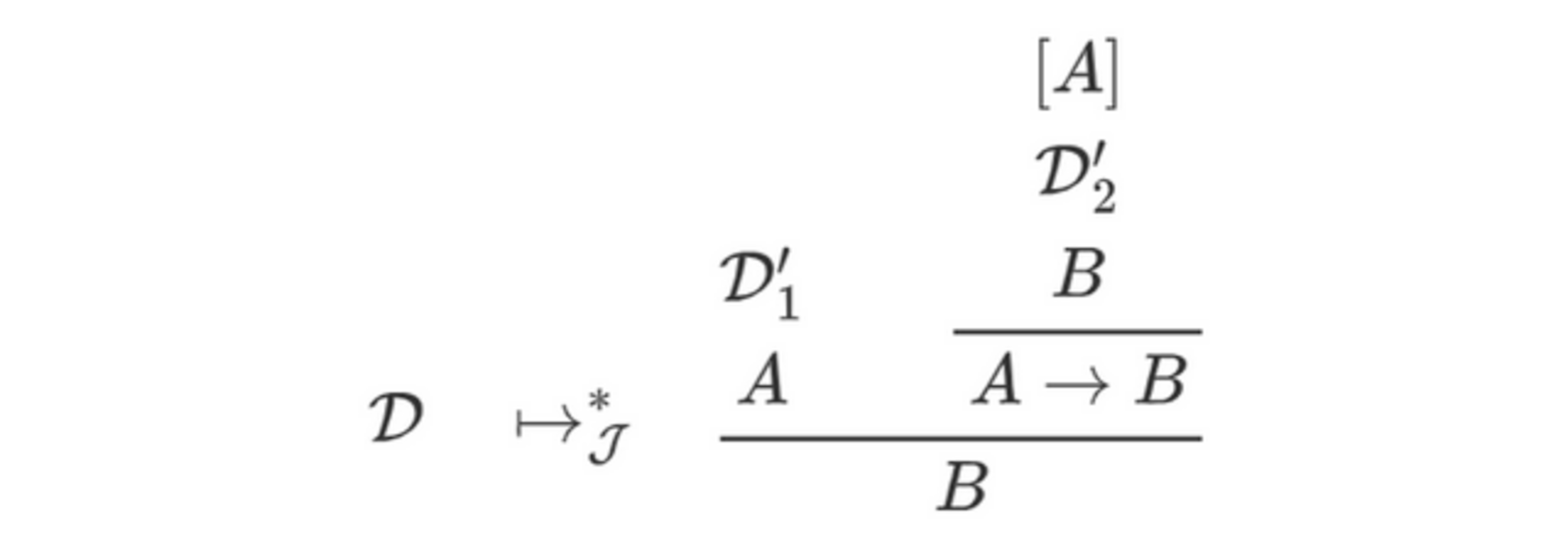
このとき右辺は閉じたカノニカルではない導出構造になり、定義7の項3に該当します。ここで、NJの導入形式特性(定理3)により、 $D$ は $J_{norm}$ によってカノニカルな導出構造に変換できます(反転原理の説明を参照)。この変換後の導出構造は妥当な導出構造を組み合わせたものなので、全体としても妥当です。よって除去則は帰結関係になっています。

$\land, \lor$ についても、同様に導入形式特性に基づいて証明ができるので、説明は割愛します。 $⊥$ については、 $⊥$ を結論に持つ妥当な導出構造は存在しないので(導入則が存在しないため)、メタレベルの爆発律から帰結関係が示されます。

NKの棄却

最後に古典論理の推論規則を批判します。すなわち、以下を示します。

NKの非健全性

証明論的意味論に対してNKは健全ではない。すなわち、ある有限集合 $Γ \subseteq Fml$ および $A \in Fml$ に対して、 $Γ ⊢_{NK} A$ かつ $Γ ⊭_{PTS} A$

排中律を反例として用います。すなわち、ある命題変数 $p$ をとり、 $A$ として $p \lor \neg p$ をとります(また、 $Γ = \emptyset$ とします)。このとき、NKの推論規則の定義より $⊢_{NK} p \lor \neg p$ です。
次に、 $⊭_{PTS} p \lor \neg p$ を示します。そのために、 $⊨_{PTS} p \lor \neg p$ を仮定します。

仮定より、ある正当化 $J$ が存在し、以下の導出構造 $D_{1}$ が $(S_{0}, J)$ -妥当になります。
$\frac{}{p \lor \neg p}$

$D_{1}$ はカノニカルではない閉じた導出構造なので、定義7の項3に該当します。 $D_{1}$ の結論が複合式であることと併せて、 $D_{1} \mapsto_{J}^{*} D_{2}$ となる $(S_{0}, J)$ -妥当でカノニカルな閉じた導出構造 $D_{2}$ が存在するといえます。このとき $D_{2}$ は定義7の項2に該当しますから、最後に適用されている推論規則が導入則であり、以下の(1), (2)いずれかのようになっています (直前の部分論証に対して同じ変数名 $D_{2}^{'}$ を使っていますが、2つのケースで $D_{2}^{'}$ は異なります)。

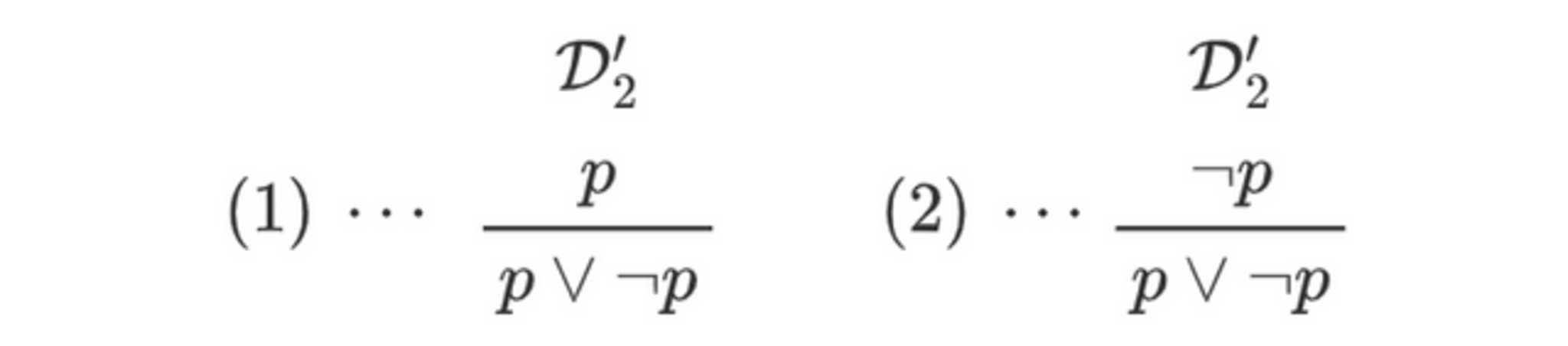
$D_{2}$ が(1)の形式になっていると仮定します。 $D_{2}$ の $(S_{0}, J)$ -妥当性より、直前の部分構造である $D_{2}^{'}$ も $(S_{0}, J)$ -妥当です。 $D_{2}^{'}$ は閉じていて結論が命題変数なので(よってカノニカルではない)、定義7の項1または3に該当します。いずれにせよ、 $D_{2}^{'} \mapsto_{J}^{*} D_{3}$ となる $(S_{0}, J)$ -妥当な $S_{0}$ の導出構造 $D_{3}$ が存在します。しかし $S_{0}$ は推論規則を持たないので、 $p$ が結論となる $S_{0}$ の導出構造は存在しません。故に矛盾します。

よって $D_{2}$ は(2)の形式になっていると分かります。 $D_{2}$ の $(S_{0}, J)$ -妥当性より、直前の部分構造である $D_{2}^{'}$ も $(S_{0}, J)$ -妥当です。 $D_{2}^{'}$ は閉じた導出構造であり、結論が複合式なので、定義7の項2または3に該当します。いずれにせよ、 $D_{2}^{'} \mapsto_{J}^{*} D_{3}$ となる $(S_{0}, J)$ -妥当でカノニカルな閉じた導出構造 $D_{3}$ が存在します。このとき定義7の項2より、 $D_{3}$ の直前の部分構造 $D_{3}^{'}$ も $(S_{0}, J)$ -妥当になります (なお、 $\neg A := A \to ⊥$ であったことを思い出しましょう)。

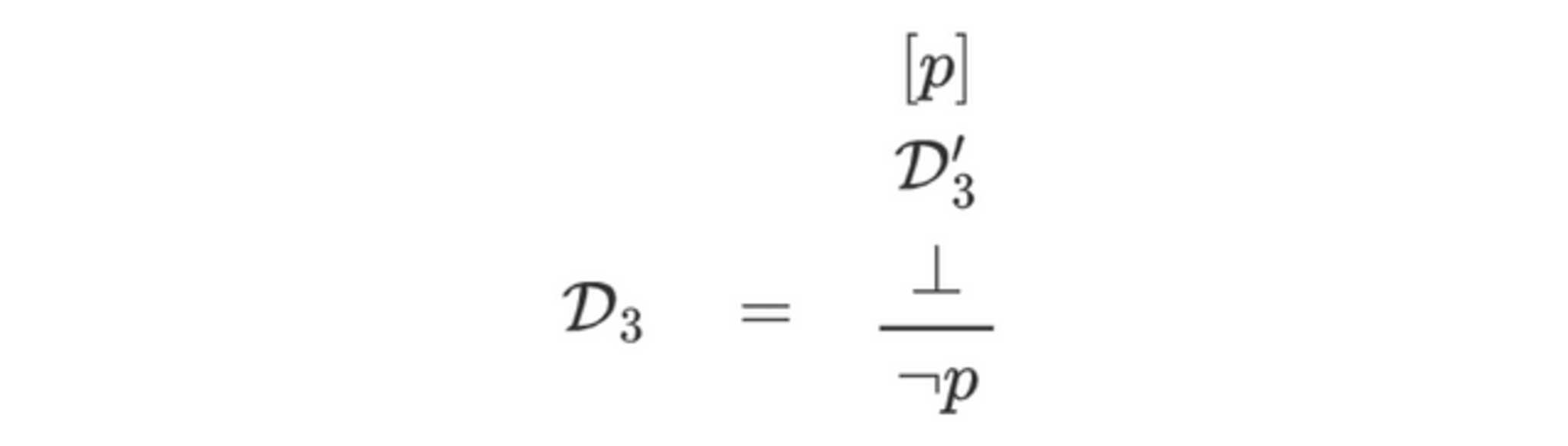
このとき、 $D_{3}^{'}$ は開いた導出構造なので、定義7の項4に該当します。よって、任意の $S^{'} \supseteq S_{0}, J^{'} \supseteq J$ 、および $(S^{'}, J^{'})$ -妥当な閉じた導出構造 $D_{4} / p$ に対して、以下の導出構造が $(S^{'}, J^{'})$ -妥当になります。

しかし、 $⊥$ には導入則がないため、 $⊥$ を結論に持つ閉じた導出構造は妥当になりえませんから、矛盾します。

以上より、 $⊭_{PTS} p \lor \neg p$ です。故に、NKは証明論的意味論に対して健全ではありません。 $◻$

その他の話題

かなり駆け足での紹介になってしまったので、たくさん抜け落ちている話題があります。それらについて本当にさわりだけ書いておきます。

批判の可能性

今回の議論はいくつかのレイヤーに別れていましたが、そのそれぞれについて批判・再反論を考えることができるでしょう。例えば、

そもそも意味の使用説を拒否してしまう
意味の使用説をもとにしつつ、真理条件による意味の理論は擁護する
証明論的意味論のアイデアは保持しつつ、「調和」の定式化の仕方を変えて、古典論理の推論規則を擁護する

などが考えられます。個人的に特に面白いと思うのは最後の議論です。例えば[大西 2012]では、自然演繹ではなくシークエント計算の体系を使うことで、古典論理を擁護するような議論が展開されています。興味がある方はぜひ。

正当化はそもそも可能なのか

今回は意味理論→論理的意味論→推論規則というかなり単純化した図式で話をしてしまいましたが、そもそもなぜこういう議論で推論規則が批判できたことになるのか、その根拠についてはかなりぼかしてしまいました。実はこの背景には、

推論規則を正当化する際にも我々は推論をするので、正当化は不可能である(cf. ルイス・キャロルのパラドックス)
古典論理を我々は今すでに使っているんだから、批判のしようがない・批判しなくてよい(cf. 全体論)

といった批判があり、これらに応答する必要があります。ダメットは実際にこの論点に関する議論をしっかりやっているので、気になる方は調べてみてください([金子 2006]の3章などに詳細な説明があります)。

完全性 (？)

終盤では、証明論的意味論に対するNJの健全性定理が登場しました。となると気になってくるのは完全性定理です。これについては実はまだよく分っていません(？！)。上で紹介した妥当性は1つの流派にすぎず、その他さまざまな定式化が提案されています。[Piecha 2016]ではいくつかの証明論的妥当性の定義が紹介されていますが、完全性が成り立つものも成り立たないものもあるようです。

というわけで、どのような意味論の定式化が適切なのか、ある程度哲学的な議論も交えながら考えていかなければならず、今はまだその発展途上ということなんでしょう。完全性までちゃんと示せないんだったら、直観主義論理を正当化できたことにはならないような気もするんですが、どうなんでしょうか。また、もし仮に完全性が成り立たないとなったら、直観主義論理と古典論理の間(中間論理)にアプローチすることになるんでしょうかね？この辺は私には全然分からないです。

反実在論

今回は全く触れませんでしたが、このダメットによる証明論的意味論のプロジェクトは、ある別の哲学的議論に結びついています。それは実在論(realism)に関する議論です。実在論とは、本当にざっくりと言えば、ある分野における何らかの対象が我々の認識から独立して「存在する」とする立場です(前編の「過去」に関する例でちらっと名前だけ出しました)。有名なのが数学における「プラトニズム」で、数というのは人間の活動から独立した実体だという主張がなされます。そしてこのような実在論に反対する立場が反実在論(anti-realism)です。ダメットは実在論と反実在論の論争は、その分野の言明について「言明の真偽が我々の認識とは関係なくどちらかに決まっている」という原理(二値原理(the principle of bivalence))を採用するかしないかの論争に帰着できるとし、そして一般には反実在論が正しいと主張します。この話に、検証超越的な真理概念への批判や、古典論理の推論規則への批判なんかも絡んでくるわけですが、直観主義論理そのものにはあまり関係ないので(あと私自身調べる余裕がなかったので)、これくらいの紹介にさせてもらいます。

想定の3倍くらい長い記事になってしまい、また、アドカレの記事と称しておきながら書き終わるのが1月中旬になってしまいましたが、お付き合いいただきありがとうございました。何か気づいた点などあればコメント欄やTwitter経由で伝えていただけると幸いです。特に、証明論的妥当性の形式的定義について触れている日本語の文献はほとんどなく、具体例を挙げている文献となると英語でもあまり見当たらないので(今のところSchroeder-Heisterの文献くらい)、今回書いた例や証明はどれも割と手探り状態でした。もし後から変なところを見つけたらいい感じに修正しておきます。

個人的な感想として、こうやって記事にして他人に説明するような文章を書いて、やっとダメットやプラウィッツが書いていたことの入り口にたどり着けたなという感じがしました。現段階の関心として、証明論的意味論が自然言語の形式意味論でどのように実現されるかが気になっているので(cf. 戸次先生の依存型意味論など)、その辺を視野に入れながら今後も精進していこうと思います。ではまた。