黄金三角形の性質の問題の解説.1

この記事はこちらに載せた問題の解説になります.

この記事では(1),(2),(3)の問題の解説をします.

(4)(5)の解説はこちら .
(6)(7)の解説はそのうち書きます.

問題文

問題
点 $A_{0}, A_{1}, A_{2}, . . .$ を次のように定めた.以下, $X Y$ で線分 $X Y$ の長さを表す.

- $△ A_{0} A_{1} A_{2}$ は $∠ A_{0}$ を頂角とした, $A_{1} A_{2} = 1$ の鋭角二等辺三角形とする.
- $△ A_{n} A_{n + 1} A_{n + 2} \sim △ A_{n + 1} A_{n + 2} A_{n + 3}$ となるように,線分 $A_{n} A_{n + 2}$ 上に点 $A_{n + 3}$ をとる.

このとき, $A_{0} A_{3} = 1$ であった.次の問いに答えよ.ただし,必要に応じて二次方程式 $x^{2} - x - 1 = 0$ の解のうち大きいほうを $φ$ としてよい.

(1) $∠ A_{0} を求めよ .$
(2) $A_{n} A_{n + 1}$ 及び $A_{n} A_{n + 3}$ を $n$ を用いて表せ.
(3) $\cos 108^{\circ}$ を求めよ.
(4) 点 $lim_{n \to \infty} A_{n}$ を $A_{\infty}$ と表す. $\vec{A_{0} A_{1}} = \vec{a}, \vec{A_{0} A_{2}} = \vec{b}$ とするとき,
$\vec{A_{0} A_{\infty}}$ を $\vec{a}$ と $\vec{b}$ の一次結合で表せ.
(5) 直線 $A_{n} A_{\infty}$ と,直線 $A_{n + 1} A_{n + 2}$ の交点を $B_{n}$ ,
直線 $A_{n + 2} A_{\infty}$ と,直線 $A_{n} A_{n + 1}$ の交点を $C_{n}$ とする.
このとき, $\frac{A_{n} A_{n + 1}}{B_{n} B_{n + 1}}$ 及び $\frac{B_{n} B_{n + 1}}{C_{n} C_{n + 1}}$ を求めよ.
(6) ある角度 $α^{\circ}$ が存在して, $△ A_{0} A_{1} A_{2}$ を $α^{\circ}$ 回転させると, $△ A_{0} A_{1} A_{2}, △ A_{1} A_{2} A_{3}, . . .$ は, $A_{\infty}$ を極とした同一の極方程式で表された曲線 $r (θ) = k^{θ}$ に接することを示せ.
(7) $k$ を求めよ.

(1)の解説

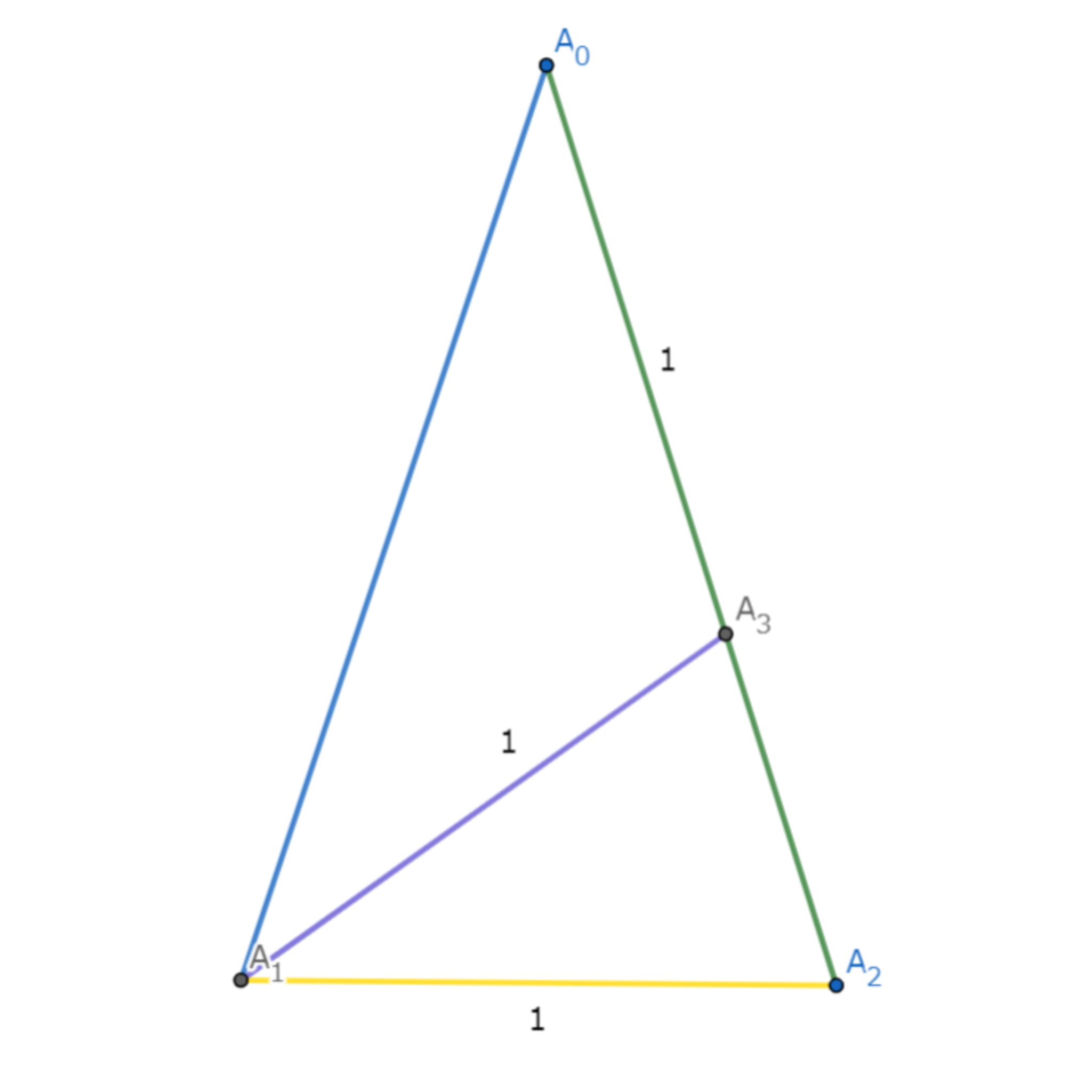(1)の図
$∠ A_{1} A_{0} A_{2} = x$ とおく. $△ A_{3} A_{0} A_{1}, △ A_{1} A_{2} A_{3}$ は二等辺三角形なので, $∠ A_{0} A_{1} A_{3} = x, ∠ A_{1} A_{3} A_{2} = ∠ A_{1} A_{2} A_{3} = 2 x$
よって, $x + 2 \times 2 x = 180^{\circ}$ であるため, $x = ∠ A_{0} = 36^{\circ}$

(2)の解説

!FORMULA[43][-1359012641][0]を求める図. $A_{0} A_{1}$ を求める図.
$A_{0} A_{1}$ を求める. $△ A_{0} A_{1} A_{2} \sim △ A_{1} A_{2} A_{3}$ であるため,
$y : 1 = 1 : (y - 1) \Leftrightarrow y^{2} - y = 1 \Leftrightarrow y = φ (> 0)$

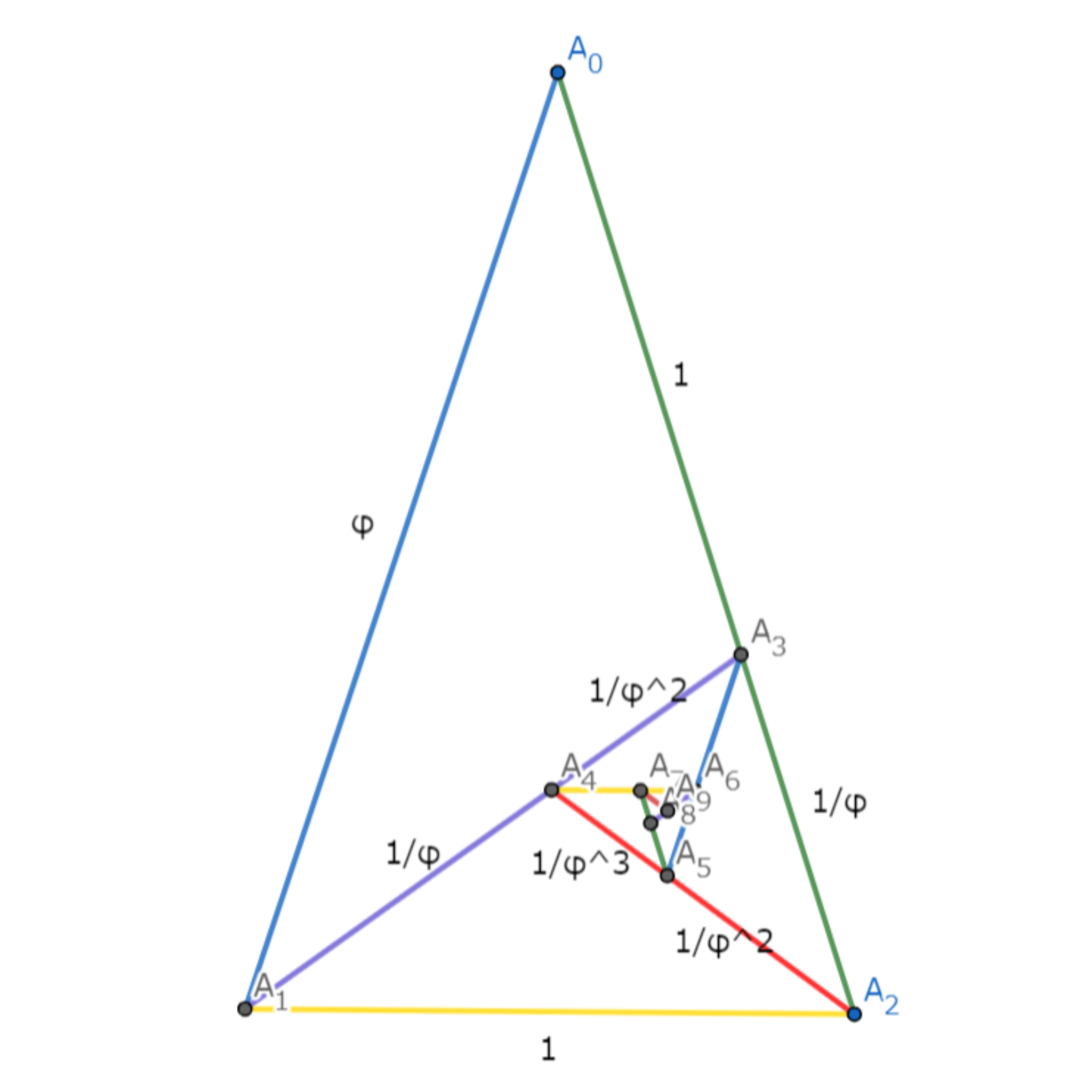各辺の長さ
$A_{0} A_{1} : A_{1} A_{2} = A_{1} A_{2} : A_{2} A_{3}$ より, $A_{2} A_{3} = \frac{1}{φ}$
また, $A_{1} A_{4} = A_{2} A_{3} = \frac{1}{φ}$
以下同様にして,
$A_{n} A_{n + 1} = \frac{1}{φ^{n - 1}}$
$A_{n} A_{n + 3} = \frac{1}{φ^{n}}$