文献あり

ピタゴラス数とガロア群のコホモロジー➀

1379

筆者は、この話題について知ったばかりの素人です。面白さを共有したくて記事を書いていますが、内容の正確性について責任が取れません。ご了承ください。

はじめに

ピタゴラス数とは、正整数の組 $(a, b, c)$ であって、 $a^{2} + b^{2} = c^{2}$ を満たすもののことである。例えば、 $3^{2} + 4^{2} = 5^{2}$ より、 $(3, 4, 5)$ はピタゴラス数である。
ピタゴラス数を全て決定することは、 $x^{2} + y^{2} = 1$ の有理数解を求めることに帰着される。その答えは知られていて、
$x = \frac{a^{2} - b^{2}}{a^{2} + b^{2}}, y = \frac{2 a b}{a^{2} + b^{2}} (a, b \in Q, (a, b) \neq (0, 0))$
が一般解となる。
この事実は、有理数の世界から飛び出して、 $Q (i)$ の世界で考えると見通しが良くなる。というのも、 $z = x + y i$ と置けば、方程式は
$| z | = 1$
と簡単になり、その解は
$z = \frac{a^{2} - b^{2}}{a^{2} + b^{2}} + \frac{2 a b}{a^{2} + b^{2}} i = \frac{a + b i}{a - b i}$
で与えられる。さらに、 $Q (i)$ の言葉で書けば、 $a + b i = w$ とおいて
$z = \frac{w}{\overset{―}{w}} (w \in Q (i)^{\times})$
と書くことができる。ここで $\overset{―}{w}$ は $w$ の複素共役である。
以降、この記事では、この $Q (i)$ 上の方程式について、話を掘り下げていく。つまり、 $Q (i)$ の元のうち、ノルムが $1$ であるものを特定せよという問いである。
尚、途中から体論についての基本的な知識を要求するが、筆者自身が素人のため、深入りはしない(できない)。コホモロジーについては、前提知識を要求しない。

ピタゴラス数の一般解

示すべき主張を改めて記そう。

$z \in Q (i)$ のとき,
$| z | = 1 \Leftrightarrow \exists w \in Q (i)^{\times}, z = w / \overset{―}{w}$

これは、単に複素数の問題として、次のように示すことができる。

$\Leftarrow$ は明らかなので, $\Rightarrow$ を示す.
$z \in Q (i)^{\times}, | z | = 1$ とする.
このとき, ある $x \in Q (i)$ が存在して,
$x + \overset{―}{x} z \in Q (i)^{\times}$ となる. ( $z \neq - 1$ なら $x = 1$ , $z = - 1$ なら $x = i$ などとすれば良い.)
$\overset{―}{x + \overset{―}{x} z} = \overset{―}{x} + x z^{- 1} = z^{- 1} (x + \overset{―}{x} z)$
より, $w = x + \overset{―}{x} z \in Q (i)^{\times}$ とおけば
$z = w / \overset{―}{w}$
となる.(証明終)

あっさり証明が終わってしまいましたが、この記事はまだ終わりません(ですます調に変えます)。
実は、上記の証明は、コホモロジーの言葉で書き直すことができ、一般化するとヒルベルトの定理90が得られます。

ヒルベルトの定理90

元の問いより一般的な場合について、同様の結果になることが知られています。

ヒルベルトの定理90

$L / K$ を有限次巡回拡大とし, そのガロア群 $G$ を $σ$ が生成するとする. このとき, $β \in L$ に対して
$N_{L / K} (β) = 1 \Leftrightarrow \exists α \in L^{\times}, β = α / σ (α)$

$K = Q, L = Q (i)$ とすれば, $G = ⟨ σ ⟩$ ( $σ$ :複素共役)であり, 定理1が従う.

この定理は、群コホモロジーを用いて以下のように表現することができます。

ヒルベルトの定理90(コホモロジー版)

$L / K$ を有限次ガロア拡大とするとき
$H^{1} (Gal (L / K), L^{\times}) = 1$

これにて、タイトルのピタゴラス数,ガロア群,コホモロジーが全て出揃いましたが、果たしてこの式はどういう意味なのでしょうか・・・

群のコホモロジー

群コホモロジー

$G$ を群, $M$ を $G$ -加群とする.
非負整数 $n$ に対して, アーベル群
$C^{n} (G, M) := {φ ∣ φ : G^{n} \to M}$
の元を $n$ -コチェインと呼ぶ.
また, 群準同型 $d^{n + 1} : C^{n} (G, M) \to C^{n + 1} (G, M)$ ,つまり $n$ 変数の写像から $n + 1$ 変数の写像を作る写像を
$d^{n + 1} (φ) (g_{1}, \dots, g_{n + 1}) = g_{1} φ (g_{2}, \dots, g_{n + 1}) + \sum_{i = 1}^{n} (- 1)^{i} φ (g_{1}, \dots, g_{i - 1}, g_{i} g_{i + 1}, g_{i + 2}, \dots, g_{n + 1}) + (- 1)^{i + 1} φ (g_{2}, \dots, g_{n + 1})$
により定める. すると, $d^{n + 1} \circ d^{n} = 0$ 満たし,このようなとき, 以下の列
$\dots \to C^{i - 1} \overset{d^{i}}{\to} C^{i} \overset{d^{i + 1}}{\to} C^{i + 1} \to \dots$
はコチェイン複体であるという.(正確な定義は他の文献を参照のこと)
さらに, $C^{n} (G, M)$ 部分群
$Z^{n} (G, M) := Ker (d^{n + 1})$
を $n$ -コサイクルと呼び,
$B^{n} (G, M) := Im (d^{n})$
を $n$ -コバウンダリと呼ぶ.ただし, $B^{0} (G, M) = 0$ と定める.
$d^{n + 1} \circ d^{n} = 0$ なので
$B^{n} (G, M) ◃ Z^{n} (G, M)$ であり,
$H^{n} (G, M) := Z^{n} (G, M) / B^{n} (G, M)$
を $n$ 次の群コホモロジーと呼ぶ.

厳密でない補足(用語に馴染めない方へ)

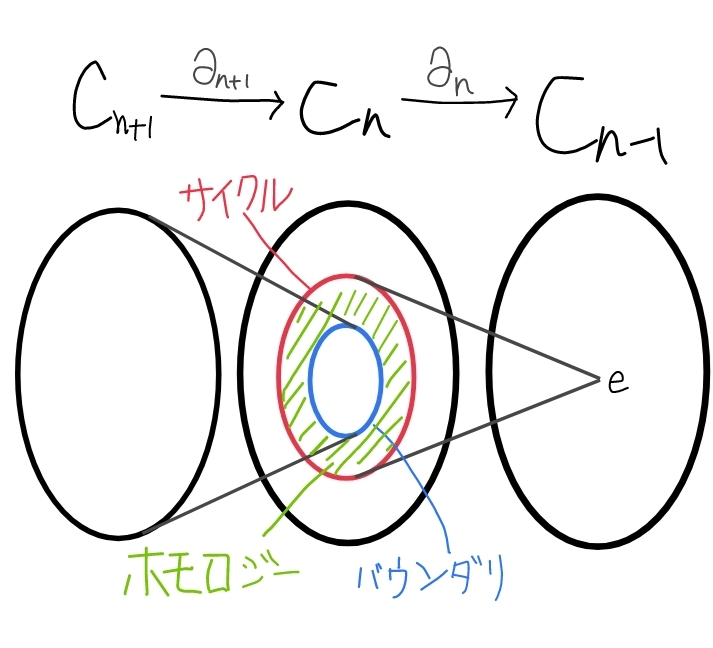
コホモロジーの用語は、双対概念であるホモロジーの方で考えた方が分かりやすいかもしれません。ホモロジーというのは、雑に言えば、コホモロジーの準同型の向きが逆になったものです。準同型として、 $n$ 次元の図形の境界をとる写像を考えましょう。(ここで言う｢図形」の意味は曖昧にしておきますが、図形が何らかの空間を張っていると考えてください。ホモロジー的にはチェインに相当します。)
図形に対して、 $2$ 回境界をとると、 $0$ になることが分かります(チェイン複体)。例えば、円盤→円周→ $0$ といった感じです。この円周のように、図形の境界として現れるもの(の集合)がバウンダリです。
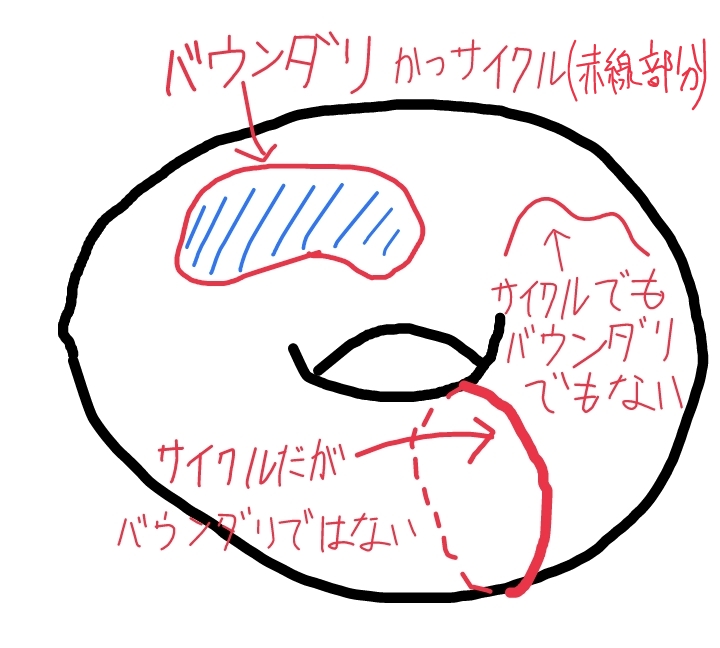
次に、サイクルの説明をします。これは、言葉のイメージ通り、端が途切れていない図形、つまり境界をとると $0$ になるもの(の集合)です。
全てのバウンダリはサイクルですが、全てのサイクルがバウンダリであるとは限りません。例えば、トーラス上に、穴に引っかけるような閉曲線を考えます。これはサイクルですが、トーラス上のいかなる面( $2$ -チェイン)の境界としても現れないので、バウンダリではありません。
トーラスの例
ホモロジー群は、このような、サイクルとバウンダリにどれくらい差があるかを表す量であり、図形的には、穴の個数などの位相幾何的な情報を持ちます。
チェイン複体

さて、長々と説明を書きましたが、今回の内容では $n = 0, 1, 2$ の場合だけ定義を把握できれば十分です。
まず, $C^{0} (G, M)$ は、一点集合から $M$ への写像全体のなす群であり、 $M$ と同型です。
次に準同型の計算をします。
$φ \in C^{0} (G, M), φ (*) = x \in M$ に対して
$d^{1} (φ) (g) = g x - x$
です。
また, $φ \in C^{1} (G, M)$ に対して,
$d^{2} (φ) (g_{1}, g_{2}) = g_{1} φ (g_{2}) - φ (g_{1} g_{2}) + φ (g_{1})$
です。
$d^{2} \circ d^{1} = 0$ が成り立つことを確認してみましょう。
$\begin{aligned} ((d^{2} \circ d^{1}) (φ)) (g_{1}, g_{2}) & = g_{1} (d^{1} (φ)) (g_{2}) - (d^{1} (φ)) (g_{1} g_{2}) + (d^{1} (φ)) (g_{1}) \\ = g_{1} (g_{2} x - x) - (g_{1} g_{2} x - x) + (g_{1} x - x) \\ = 0 \end{aligned}$
なので、ちゃんとコチェイン複体になっていることが確認できました。

ピタゴラス数再論

群コホモロジーの準備が整ったので、実際に $G = Gal (Q (i) / Q) = ⟨ σ ⟩, M = Q (i)^{\times}$ としてコホモロジーの計算をしていきます。今回、 $M$ は乗法群なので、今まで足し引きで書いていたものは掛け割りに変わることに注意してください。

1-コサイクル

$φ \in C^{1} (G, M), φ (σ) = α$ とします。
$φ \in Z^{1} (G, M)$
$\Leftrightarrow \forall i, j \in {0, 1} φ (σ^{i}) σ^{i} φ (σ^{j}) = φ (σ^{i + j})$
$\Leftrightarrow \forall i, j \in {0, 1} α^{i} σ^{i} (α^{j}) = φ (σ^{i + j})$
$\Leftrightarrow α σ (α) = φ (σ^{2})$
$\Leftrightarrow | α | = 1$
より,
$| α | = 1 \Leftrightarrow φ \in Z^{1} (G, M)$
が分かります。つまり、ノルムが $1$ の元を全て求めることは、ガロア群の1-コサイクルを全て求めることだったんですね。
ここで、ヒルベルトの定理90(コホモロジー版)が活躍します。この定理の主張は
$Z^{1} (G, M) = B^{1} (G, M)$
でした。従って、問題は $1$ -コバウンダリの計算に帰着されます！

$1$ -コバウンダリ

コバウンダリの計算は簡単です。 $ψ \in C^{0} (G, M), ψ (*) = x$ に対して,
$d^{1} (ψ) (σ) = x^{σ} x^{- 1} = \overset{―}{x} / x$
です。
これらの結果を合わせると
$| α | = 1$
$\Leftrightarrow φ \in Z^{1} (G, M)$
$\Leftrightarrow φ \in B^{1} (G, M)$
$\Leftrightarrow \exists x \in Q (i)^{\times}, α = \overset{―}{x} / x$
となり、元の問題をコホモロジーの問題として扱い、同じ結果を得ることができました！
次回は、今回の複素数による解法をコホモロジーの言葉に変換することで、ヒルベルトの定理90を一般的な場合について証明します。