文献あり

グラフによる碁の表現

417

グラフ理論

グラフ理論の基本

集合 $S$ の $n$ 元からなる部分集合全体を $[S]^{n}$ と書く。

形式的に書けば $[S]^{n} = {X \subset S ∣ | X | = n}$ となる。
グラフとは図1のように「頂点」と「辺」からなる図形である。グラフを考えるうえでは頂点の位置や辺の長さや形は考えず、頂点と辺の接続関係に着目する。具体的な例としては路線図などを考えるとよいだろう。路線図は駅のつながりに注目した図であり、駅がどの路線でつながっているかは正確に表すが、線は現実の線路の形通りではないし駅の位置も現実通りではない。

頂点は辺によってほかの頂点とつながっている。辺は二つないし一つの頂点に接続している。二頂点間に複数の辺があるとき、これを多重辺という。ある辺の両端点が等しいとき、これをループという。図1の $e_{5}$ 、 $e_{6}$ が多重辺であり、 $e_{2}$ がループである。多重辺もループもないグラフを単純グラフといい、多重辺やループを含むグラフを多重グラフという。

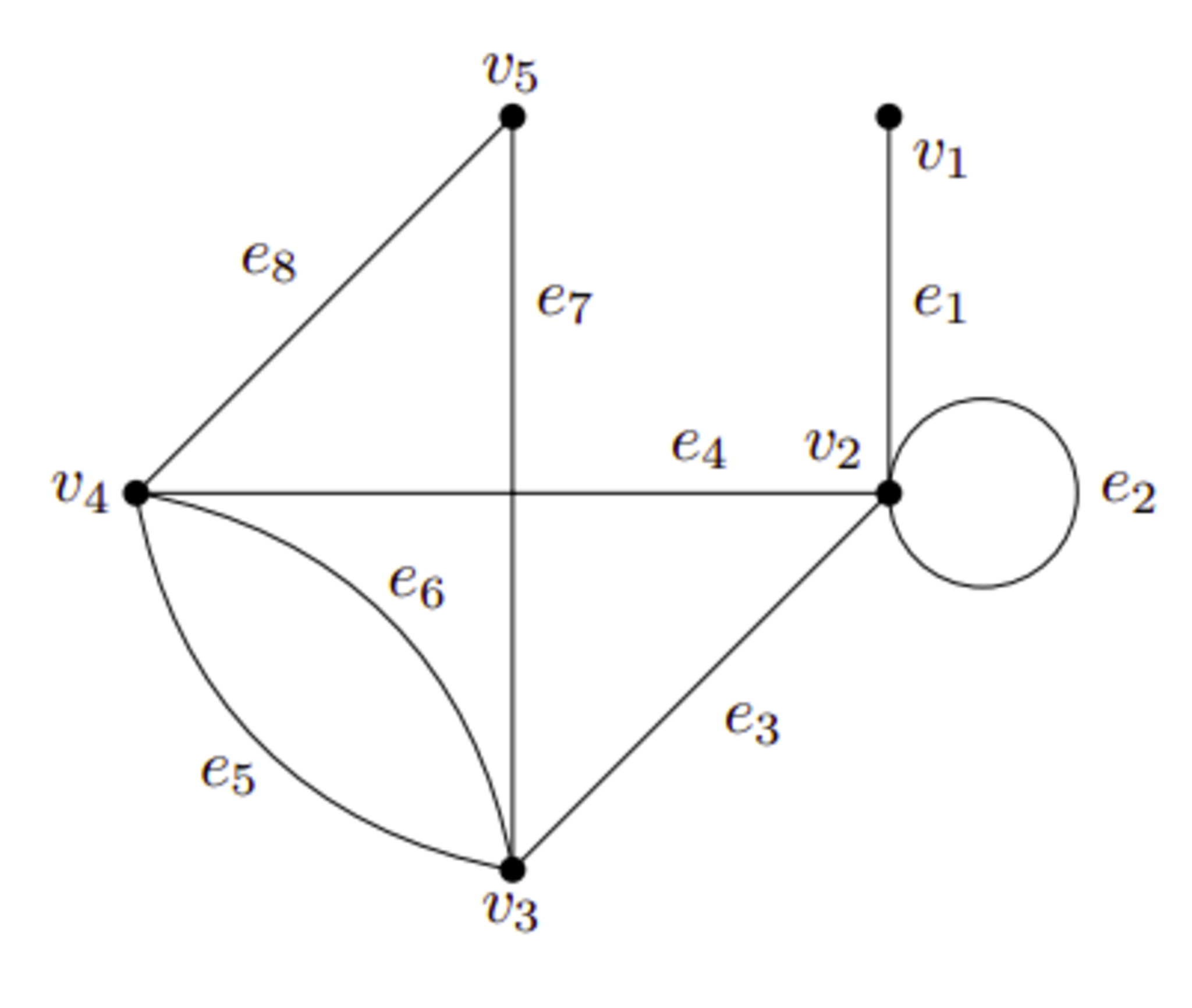グラフの例

形式的には、グラフは以下のように定義される。

頂点集合 $V$ 、辺集合 $E$ 、接続写像 $ψ : E \to [V]^{1} \cup [V]^{2}$ の組 $G = (V, E, ψ)$ をグラフという。

例えば図1で考えると、 $V = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}}$ 、 $E = {e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}}$ であり、接続写像 $ψ$ は $\begin{aligned} ψ (e_{1}) & = {v_{1}, v_{2}} \\ ψ (e_{2}) & = {v_{2}} \\ ψ (e_{3}) & = {v_{2}, v_{3}} \\ ψ (e_{4}) & = {v_{2}, v_{4}} \\ ψ (e_{5}) & = {v_{3}, v_{4}} \\ ψ (e_{6}) & = {v_{3}, v_{4}} \\ ψ (e_{7}) & = {v_{3}, v_{5}} \\ ψ (e_{8}) & = {v_{4}, v_{5}} \end{aligned}$
となっている。このとき、辺 $e \in E$ に対して $ψ (e) = {u, v}$ の元を $e$ の端点と呼び、辺 $e$ は頂点 $u, v$ に接続する、頂点 $u, v$ は $e$ によって結ばれる、頂点 $u, v$ は互いに隣接している、などという。 $ψ (e) = {u, v}$ であるとき、 $e = u v$ と書く。

グラフ $G = (V, E, ψ)$ において、相異なる $e, e^{'} \in E$ が $ψ (e) = ψ (e^{'})$ を満たすとき、 $e, e^{'}$ を多重辺と呼ぶ。また、 $e \in E$ に対し $ψ (e)$ がただ一つの頂点からなるとき、これをループと呼ぶ。多重辺またはループを含むグラフを多重グラフといい、どちらも含まないものを単純グラフという。

単純グラフ $G = (V, E, ψ)$ に関して、接続写像 $ψ$ は単射であり、値域は $[V]^{2}$ となる。よって $E \subset [V]^{2}$ としてしまっても構わない。ここで、 $e = {u, v} \in E$ は頂点 $u$ 、 $v$ を結ぶとする。このとき接続写像は辺集合 $E$ から自然に定まるので、単純グラフは頂点集合と辺集合の組 $G = (V, E)$ で表す。

グラフ $G$ の頂点集合を $V (G)$ 、辺集合を $E (G)$ 、接続写像を $ψ_{G}$ で表す。グラフと頂点集合や辺集合を厳密に区別しない場合も多くある。すなわち、 $v \in V (G)$ と書くべきところを $v \in G$ と書いたりする。

図2の二つのグラフは頂点と辺のつながり方が一緒である。このようなグラフを同型なグラフという。

グラフ $G = (V, E, ψ)$ 、 $H = (V^{'}, E^{'}, ψ^{'})$ に対し、全単射 $f : V \to V^{'}$ 、 $g : E \to E^{'}$ が存在し、 $ψ (e) = {u, v} \Leftrightarrow ψ^{'} (g (e)) = {f (u), f (v)}$ であるとき、 $G$ と $H$ は同型であるといい $G ≅ H$ と書く。

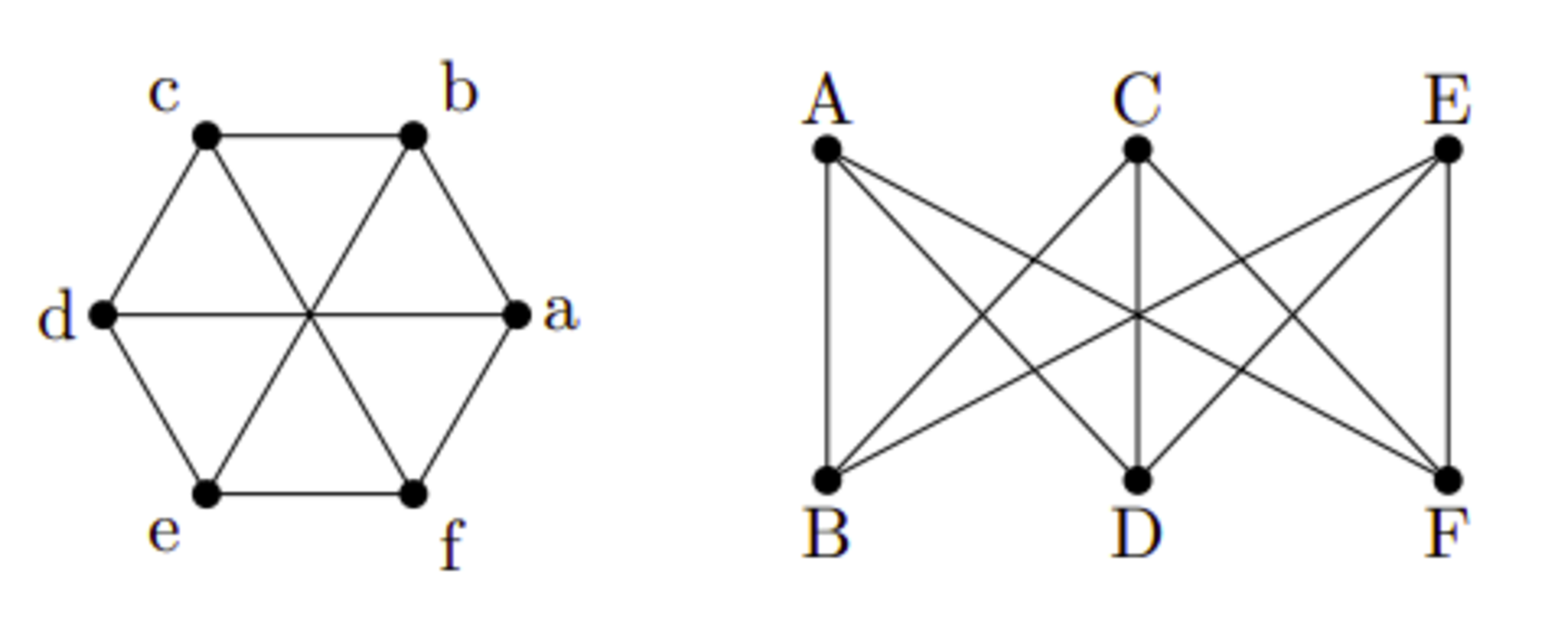同型なグラフ

グラフ ${\emptyset, \emptyset, ψ}$ を空グラフという。

集合 $A, B \subset V$ に対し、辺 $e = u v$ が $u \in A$ 、 $v \in B$ を満たすとき、これを $A$ - $B$ 辺という。

$A$ - $B$ 辺全体の集合を $E (A, B)$ と表す。 $E ({u}, B)$ や $E (A, {v})$ を単に $E (u, B)$ 、 $E (A, v)$ と書き、 $u$ - $B$ 辺などという。頂点 $v$ に接続する辺全体の集合を $E (v)$ で表す。

頂点 $v \in V$ の隣接点全体の集合を $Nei (v)$ と書く。さらに、 $U \in V$ に対して、 $U$ 内の頂点の隣接点で $V ∖ U$ に属するもの全体の集合を $Nei (U)$ と書く。

グラフ $G = (V, E, ψ)$ と $G^{'} = (V^{'}, E^{'}, ψ^{'})$ について $V^{'} \subset V$ かつ $E^{'} \subset E$ であって、任意の $e^{'} \in E^{'}$ に対し $ψ^{'} (e^{'}) = ψ (e^{'})$ となるとき、 $G^{'}$ を $G$ の部分グラフであるといい、 $G^{'} \subset G$ と書く。

グラフの辺に向きを考えたものを有向グラフという。これに対し、向きのないグラフを無向グラフという。有向グラフでは辺が集合ではなく組で表される。例えば、 $e_{1} = (v_{2}, v_{1})$ である。有向グラフもまた $(V, E, ψ)$ という組で表されるが、接続写像は $ψ : E \to V^{2}$ となる。

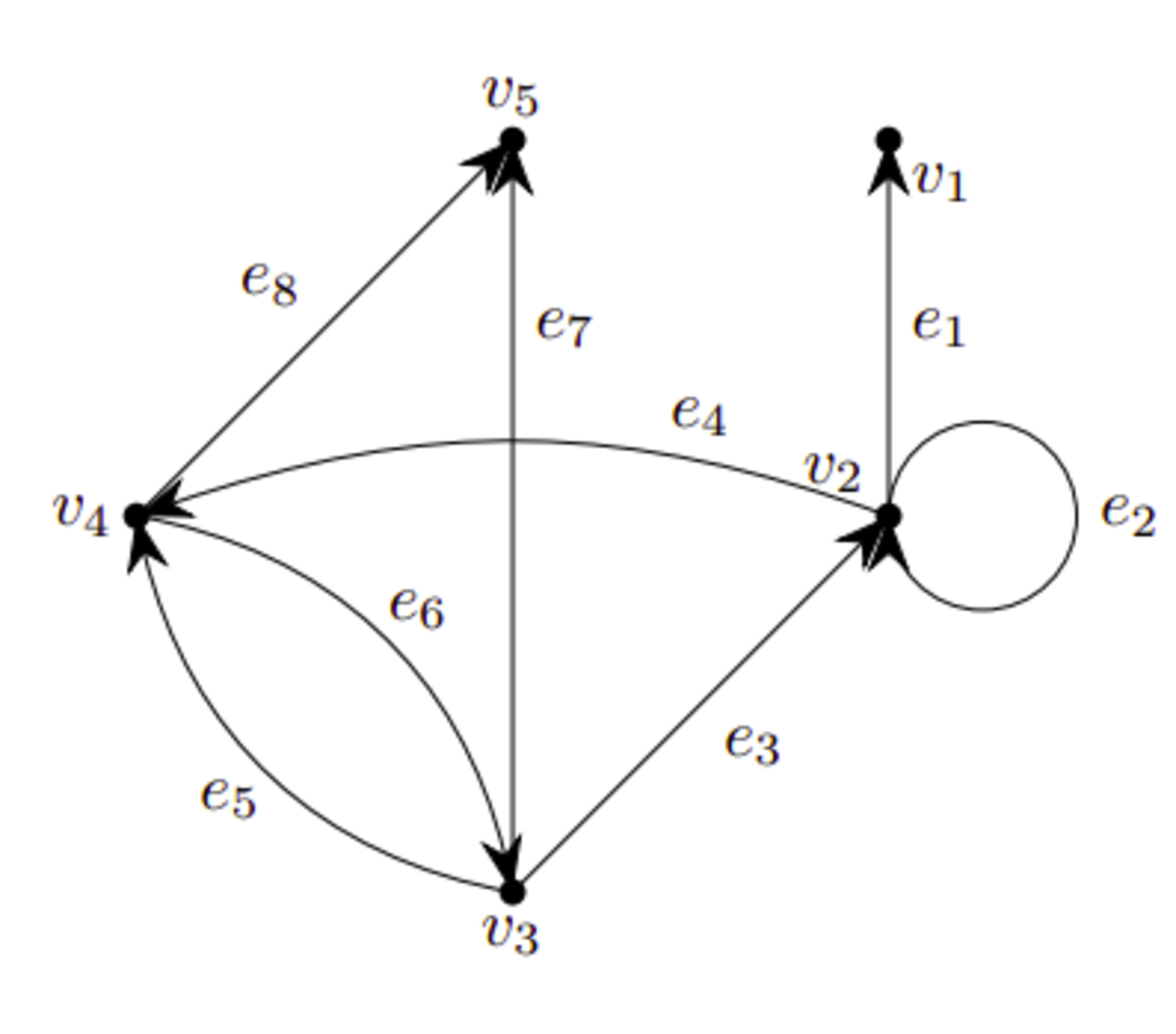有向グラフの例

道

頂点と辺を交互に並べた空でない有限列 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ で各 $i \leq k$ に対し $e_{i} = v_{i - 1} v_{i}$ となるものを歩道という。また $v_{0}$ 、 $v_{k}$ を端点と呼び、特に $v_{0}$ を始点、 $v_{k}$ を終点と呼ぶ。

歩道 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ が相異なる $i, i^{'} \leq k$ に対し $e_{i} \neq e_{i^{'}}$ であるとき、これを小径という。さらに相異なる $j, j^{'} \leq k$ に対し $v_{j} \neq v_{j^{'}}$ であるとき、これを道という。

歩道（小径、道）の辺の本数をその長さという。始点と終点は本質的には違いがないが、これを決めておくことで歩道内の要素に順番が与えられるので便利なことがある。小径は頂点の重複を許す道、歩道は辺の重複を許す道、というとらえ方もできる。

道の例

道はその頂点の集合 $V (P)$ と辺の集合 $E (P)$ からなる単純グラフ $P = (V (P), E (P))$ ととらえることもできる。道を表すために、その頂点だけを並べることも多い。そのようなときは $P = v_{0} \dots v_{k}$ と書く。

$0 \leq i \leq j \leq k$ とする。道 $P = v_{0} \dots v_{k}$ の一部を切り取ったものを以下のように表す。

$\begin{aligned} v_{i} P & = v_{i} \dots v_{k} \\ P v_{j} & = v_{0} \dots v_{j} \\ v_{i} P v_{j} & = v_{i} \dots v_{j} \\ \overset{˚}{P} & = v_{1} \dots v_{k - 1} \\ \overset{˚}{v_{i}} P & = v_{i + 1} \dots v_{k} \\ P \overset{˚}{v_{j}} & = v_{0} \dots v_{j - 1} \end{aligned}$

$P$ が長さ1の道であるとき、 $\overset{˚}{P}$ は空グラフである。これはもはや道ではない。

さらに、いくつかの道をつないで新たな道を作るとき、たとえば三本の道の和 $P x \cup x Q y \cup y R$ が道になるならば、これを単に $P x Q y R$ というように表す。

道 $P = v_{0} \dots v_{k}$ と頂点の集合 $A$ 、 $B$ について $V (P) \cap A = {v_{0}}$ かつ $V (P) \cap B = {v_{k}}$ となるとき、 $P$ を $A - B$ 道という。

$A$ - $B$ 道全体の集合を $Path (A, B)$ で表す。以前と同様に波括弧を省略し $Path (v_{0}, B)$ などと書いたりする。

グラフ $G = (V, E, ψ)$ について、任意の $u, v \in V$ に対し $Path (u, v) \neq \emptyset$ となるとき、 $G$ は連結であるという。

直観的に言えばすべてつながっているグラフが連結なグラフである。

極大な連結部分グラフを連結成分という。

縮約

グラフのある辺を縮めて一つの頂点にすることを考えよう。

図5のようにグラフ $G = (V, E)$ の辺 $e = x y \in E$ を選ぶ。この辺を新しい頂点 $v_{e}$ に置き換える。このとき、 $x$ または $y$ と隣接していた頂点は $v_{e}$ と隣接するようにし、どちらとも隣接していない頂点は $v_{e}$ とも隣接しないようにする。

縮約

こうして得られたグラフを、 $G$ から、その辺 $e = x y$ を1つの頂点 $v_{e}$ に縮約して得られたグラフといい、 $G / e$ で表す。 $G / e$ の頂点集合と辺集合は、形式的には以下のように表される。
$\begin{aligned} V (G / e) & = (V ∖ {x, y}) \cup {v_{e}} \\ E (G / e) & = {v w \in E ∣ {v, w} \cap {x, y} = \emptyset} \cup {v_{e} w ∣ x w \in E ∖ {e} または y w \in E ∖ {e}} \end{aligned}$
この縮約の操作を何度か繰り返し、 $G$ から新たにグラフ $X$ を作ることを考える。各 $x \in V (X)$ に対し、 $x$ に縮約された $G$ の頂点全体の集合を $V_{x}$ とすると、各 $V_{x}$ は連結であり、任意の $x, y \in V (X)$ に対し、 $G$ に $V_{x} - V_{y}$ 辺があることと、 $x y \in E (X)$ となることが同値である。集合 $V_{x}$ を $G$ の分岐集合という。

グラフ碁とは

いよいよグラフを用いて碁について考える。終局がわかりやすい純碁を基に考える。純碁について詳しくはこちら https://note.com/kurosen0000/n/nb2db700f9b95

まず、碁盤について考えてみよう。碁盤は交点を頂点とみなせばグラフととらえられる。碁盤が多重辺やループを持っていたとしても、碁を打つうえでは特に意味を持たない。これは、石の存在にはどの交点が隣接しているのかさえわかればよいからである。例えば、図6は九路盤に三本の辺を加えているが、それが在ろうとなかろうと黒石は取られている。したがって碁盤は単純グラフとしてしまってよい。

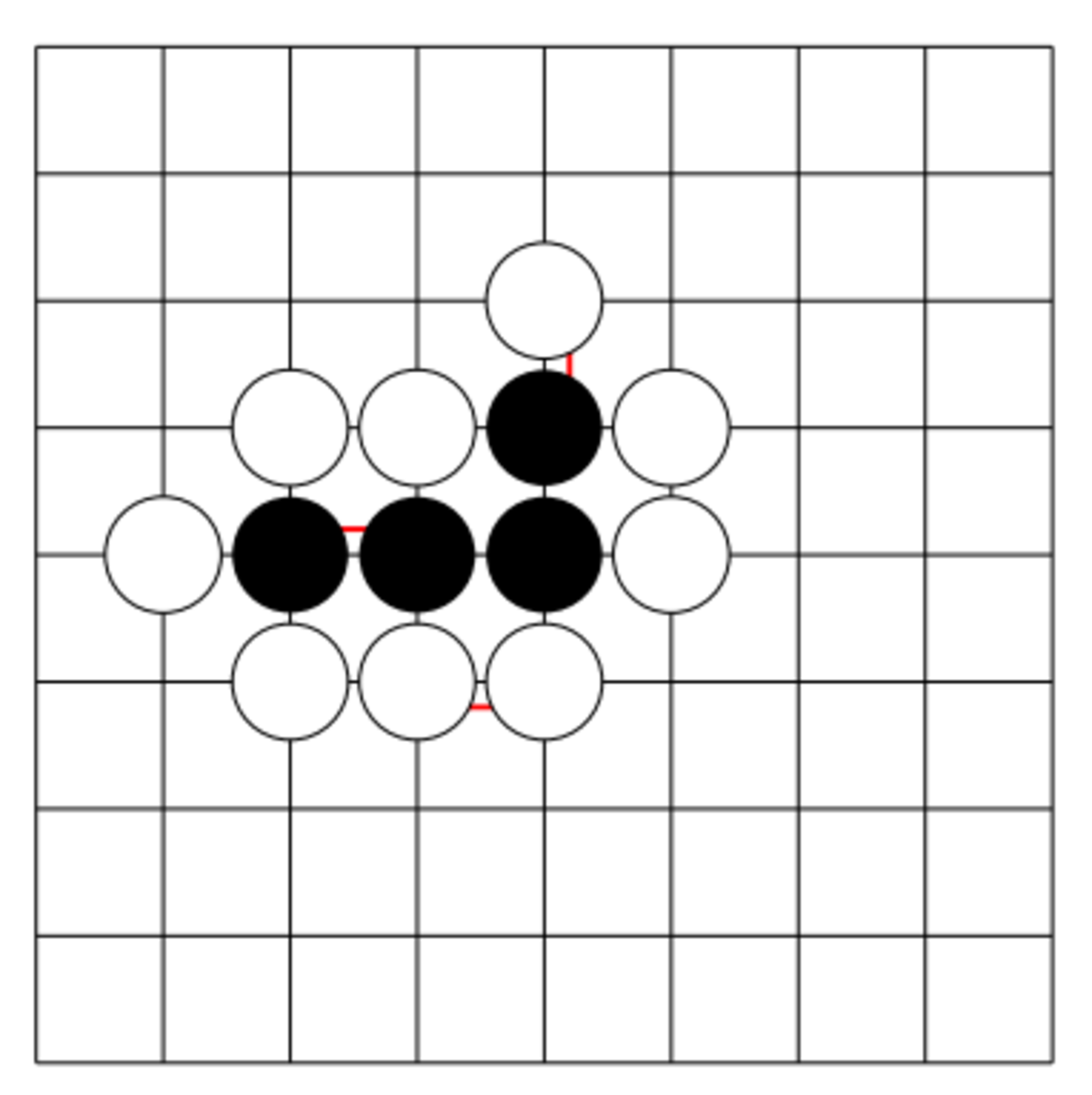多重辺と石の存在

さらに、碁盤は連結グラフとしてしまってよい。というのも、ある連結成分に打たれた
石がほかの連結成分に在る石の存在にかかわることはないので、それぞれの連結成分の中だけで考えれば十分だからである。

連結な単純グラフを碁グラフと呼ぶ。

以下、特に断らない限り $G = (V, E)$ は碁グラフであるとする。

碁盤を用意したので、次は石について考えよう。交点は「黒が置かれている」「白が置かれている」「空点である」の三つのうちいづれかの状態にある。よって、例えば黒を-1、白を1、空点を0とすれば、写像 $f : V \to {- 1, 0, 1}$ と盤面が同一視できることとなる。つまり $f (v) = - 1$ のとき交点 $v$ には黒石が置かれていると考えるのである。

$c : V \to {- 1, 0, 1}$ を配置}と呼ぶ。配置全体の集合を $C$ で表す。配置 $c$ に対し、 $B := c^{- 1} ({- 1})$ 、 $W := c^{- 1} ({1})$ 、 $N := c^{- 1} ({0})$ とし、これを頂点集合 $V$ の分割とみて $c = (B, W, N)$ と表すこともある。

$B$ 、 $W$ 、 $N$ が $c$ により定められることを強調したいときは $B_{c}$ 、 $W_{c}$ 、 $N_{c}$ などと書いたりする。

例えば図7では $B = {v_{2}, v_{4}, v_{6}}, W = {v_{5}, v_{8}}, N = {v_{1}, v_{3}, v_{7}, v_{8}}$ となる。

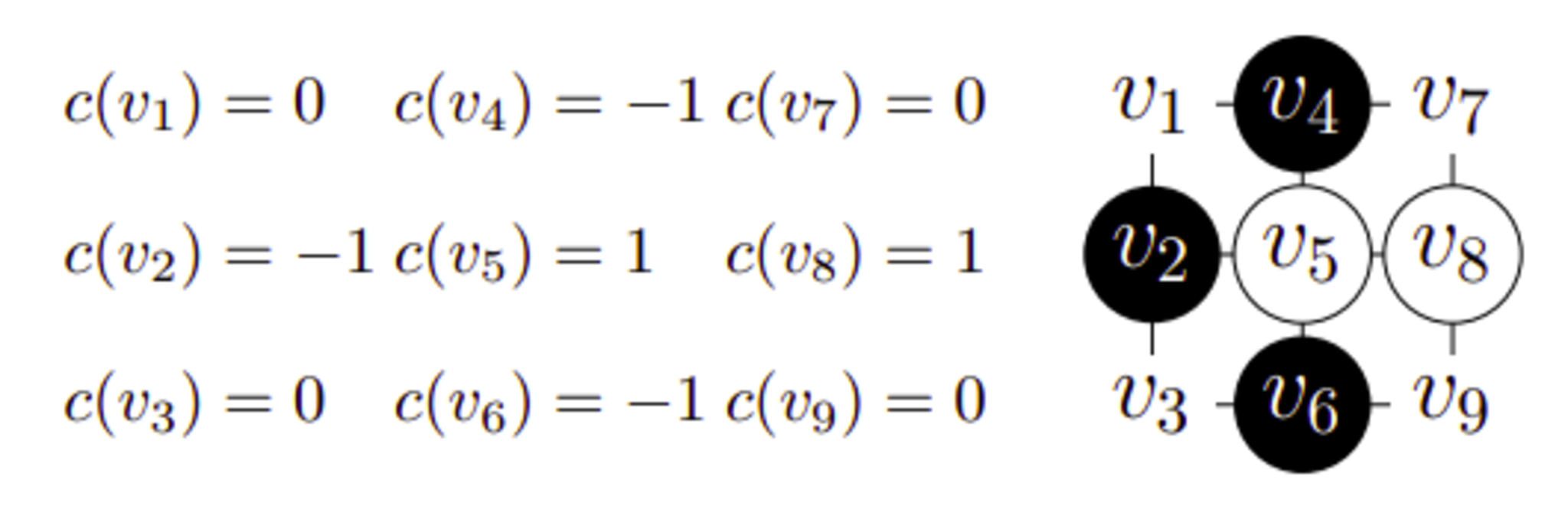配置の例

$V = B ⊔ W ⊔ N$ であるから、 $B$ 、 $W$ が定まればおのずと $N$ も定まる。そのため、 $C = (B, W)$ と略すことがある。

碁盤上で「つながっている」石のかたまりを連という。碁盤と配置の同一視の方法から、ある二つの石が碁盤上でつながっていることと、その二つの頂点が分割集合の同じ連結成分に属していることが同じ意味になる。

$v, w \in V$ 、 $c \in C$ とする。 $v \sim_{c} w$ であるとは $\exists P \in Path (v, w) s . t . V (P) \subset c^{- 1} ({c (v)})$ を満たすことである。

$c (v)$ は $v$ の石の色を表す。なので $c^{- 1} ({c (v)})$ は $v$ と同じ色の分割集合となる。たとえば $v \in B$ のときは $c^{- 1} ({c (v)}) = c^{- 1} ({- 1}) = B$ となる。さらに $v - w$ 道 $P$ の頂点 $V (P)$ が黒の部分集合であるから、当然 $w \in B$ であり $v, w$ が黒石だけからなる道で結べることを表している。この同値関係による同値類（のうち黒か白に含まれるもの）が連となる。

$c$ を配置とする。 $\sim_{c}$ は同値関係である。

任意の $v \in B \cup W$ に対して、道 $P = v$ は $V (P) \subset c^{- 1} ({c (v)})$ を満たす。
任意の $v, w \in V$ をとる。 $v \sim_{c} w$ ならば、ある道 $P \in Path (v, w) = Path (w, v)$ が存在して $V (P) \subset c^{- 1} ({c (v)})$ を満たす。このとき $c^{- 1} ({c (v)}) = c^{- 1} ({c (w)})$ であるから $w \sim_{c} v$ 。
任意の $u, v, w \in V$ をとる。 $u \sim_{c} v$ かつ $v \sim_{c} w$ であるならばある道 $P_{1} \in Path (u, v)$ 、 $P_{2} \in Path (v, w)$ が存在して、 $V (P_{1}) \subset^{- 1} ({c (u)})$ 、 $V (P_{2}) \subset^{- 1} ({c (v)})$ を満たす。このとき $c^{- 1} ({c (u)}) = c^{- 1} ({c (v)})$ であるから、道 $P = P_{1} v P_{2}$ は $V (P) \subset c^{- 1} ({c (u)})$ を満たす。よって $u \sim_{c} w$

$c \in C$ 、 $v \in V$ とする。 $[v]_{c} := {w \in V ∣ v \sim_{c} w}$ 、
$V / \sim_{c} := {[v]_{c} ∣ v \in V}$ 、 $E / \sim_{c} := {{[v]_{c}, [w]_{c}} \in [V / \sim_{c}]^{2} ∣ v w \in E}$
とし、 $G / \sim_{c} := (V / \sim_{c}, E / \sim_{c})$ と定める。

$G / \sim_{c}$ は $G$ の縮約となっている。さらに隣接する頂点は違う色からなる交点の集合になっていて、その作り方から $G / \sim_{c}$ は三部グラフになっている。

さて、配置は碁盤に石を置いただけであり、碁の局面としては適しないものも含まれている。具体的に言えば、取られた状態にある石が存在してはいけない。石が存在するための条件はその石のかたまりが空点に隣接していることで、例えば日本囲碁規約の第四条がそれにあたる。

まずは、いわゆる呼吸点を定義する。

配置 $c = (B, W, N)$ とする。\ruby[g]{呼吸点集合}{liverty} $l : B \cup W \to 2^{N}$ を以下のように定める。
$l (v) = {w \in N ∣ \exists u \in [v]_{c} s . t . u w \in E}$

式中の $u$ は $[v]_{c}$ 内の点なので、 $v$ と同じ色の石だけでつながっている（もちろん $u = v$ でもよい）。その $u$ が空点 $w$ と隣接しているので $v$ は盤上に存在できる。 $l (v) = \emptyset$ のときはそのような空点がないので $v$ は存在できない。

定義より明らかに $l (v) \subset Nei ([v]_{c})$ である。

配置 $c$ における呼吸点集合であることを強調するときは $l_{c}$ などと書く。

配置 $c \in C$ が盤面であるとは、任意の $v \in B \cup W$ に対し、 $l (v) \neq \emptyset$ となることである。盤面全体の集合を $C^{*}$ と書く。

例えば、図8は盤面でない配置の例である。白□は呼吸点集合が空になっている。

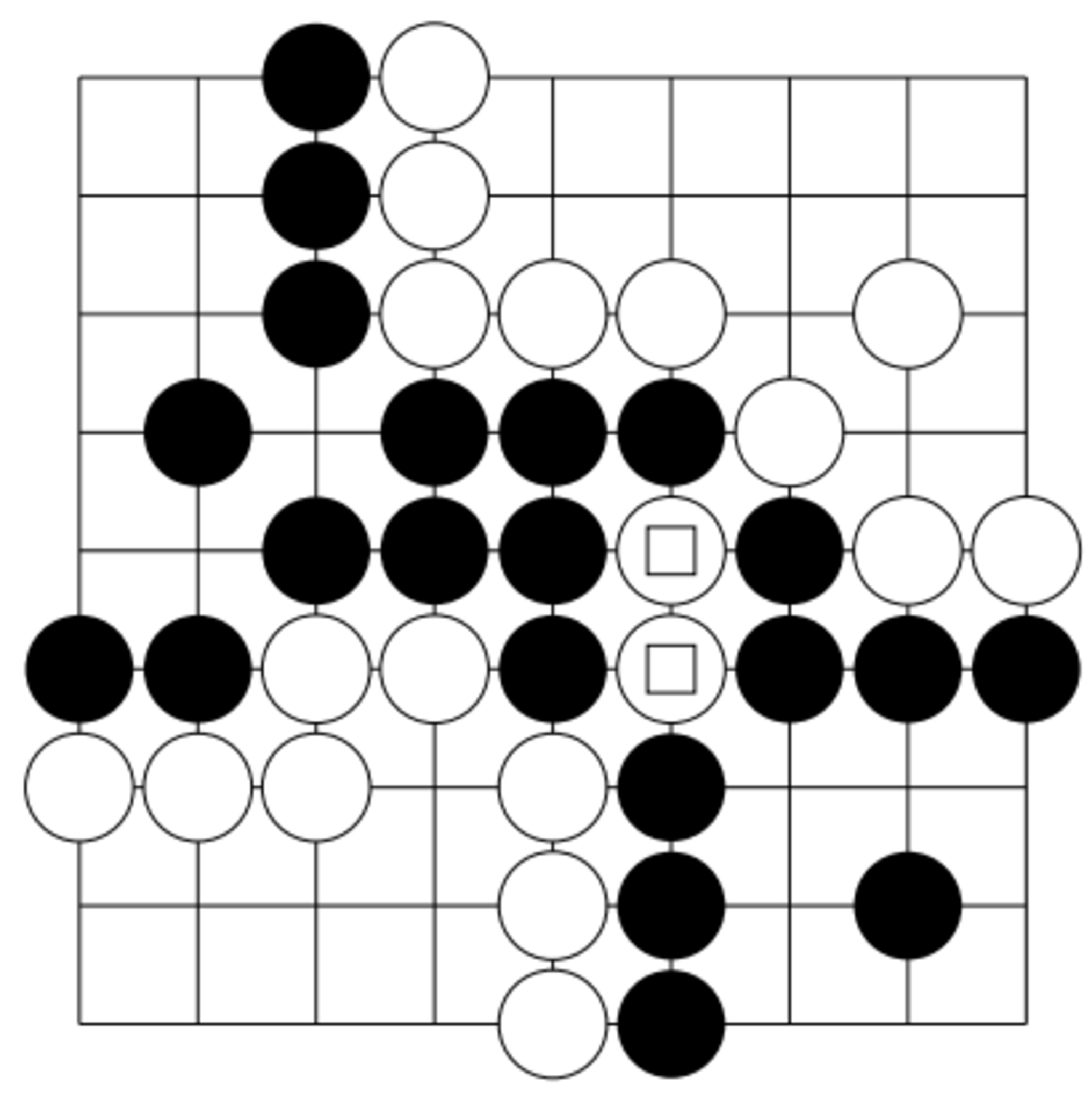盤面でない例

$c = (B, W, N)$ を配置, $v \in N$ とする. $c + v, c - v$ を以下で定める.
$\begin{aligned} B_{c - v} & = B_{c} \cup {v} \\ W_{c - v} & = W_{c} ∖ l_{c}^{- 1} ({v}) \\ N_{c - v} & = (N_{c} ∖ {v}) \cup (l_{c}^{- 1} ({v}) \cap W_{c}) \end{aligned}$
$\begin{aligned} B_{c + v} & = B_{c} ∖ l_{c}^{- 1} ({v}) \\ W_{c + v} & = W_{c} \cup {v} \\ N_{c + v} & = (N_{c} ∖ {v}) \cup (l_{c}^{- 1} ({v}) \cap B_{c}) \end{aligned}$

$c - v$ は配置 $c$ において $v$ に黒石を打った場合、 $c + v$ は配置 $c$ において $v$ に白石を打った場合に対応している。

$l_{c}^{- 1} ({v}) \cap W_{c}$ は $W_{c}$ の頂点のうち, $v$ のみを呼吸点に持つものの集合である. $v$ を呼吸点に持つ頂点の集合ではない. つまり、 $l_{c}^{- 1} ({v}) \cap W_{c}$ は黒が $v$ に打ったときに取りあげられる白石全体の集合である。

図9において $v \in l^{- 1} ({u})$ であるが、 $v^{'} \notin l^{- 1} ({u_{1}})$ である。これは $l (v^{'}) = {u_{1}, u_{2}, u_{3}, u_{4}} \neq {u_{1}}$ であるからだ。

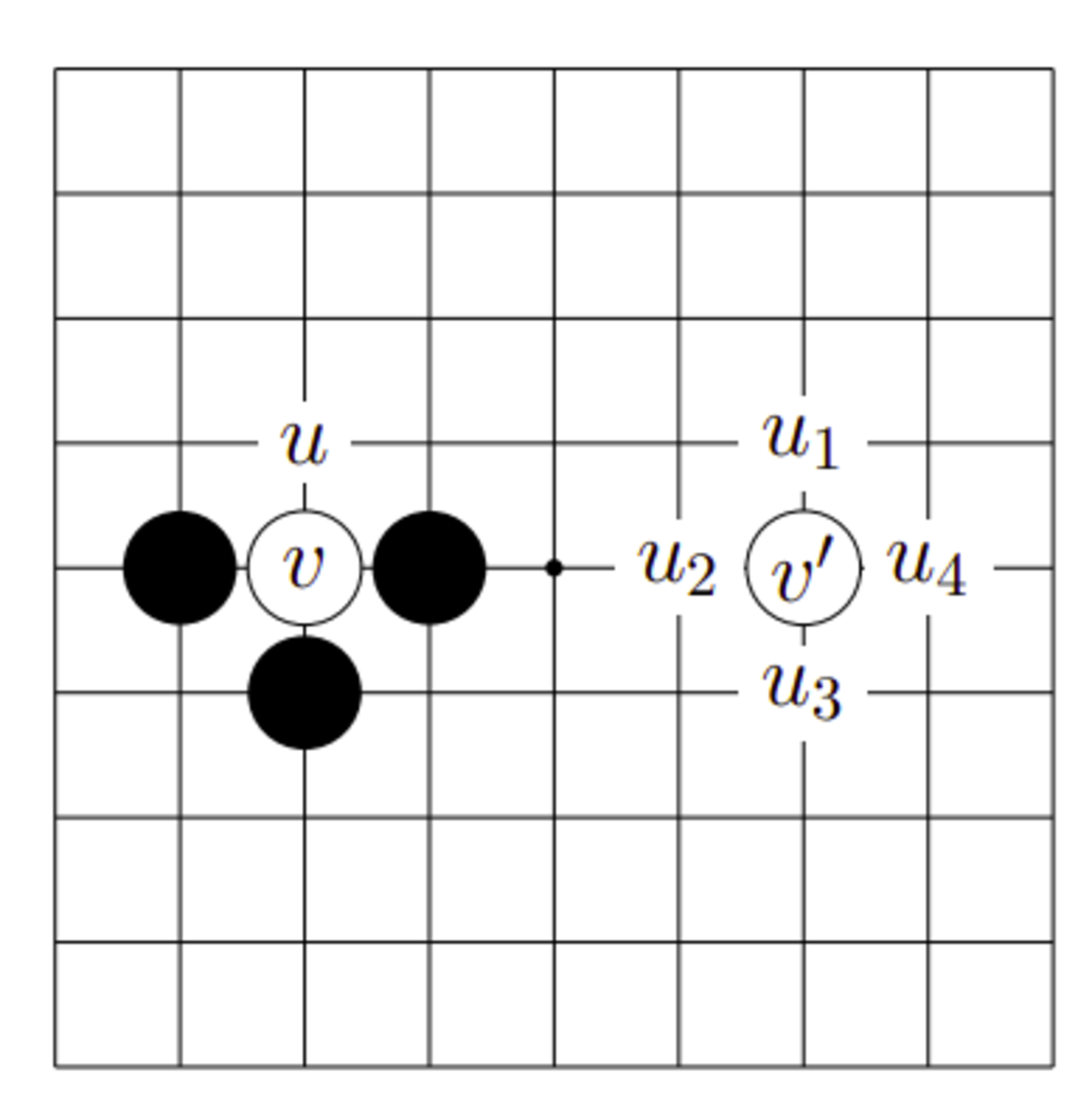呼吸点集合

定義18では $c$ 、 $c - v$ 、 $c + v$ は配置ではあるものの盤面とは限らない。正規の着手では、着手前も着手後も盤面となっている必要がある。

$M$ を以下で定め, $M$ の元 $m = (c, d)$ を着手という.
$\begin{aligned} M^{-} & := {(c, d) \in C^{*} \times C^{*} ∣ \exists v s . t . d = c - v} \\ M^{+} & := {(c, d) \in C^{*} \times C^{*} ∣ \exists v s . t . d = c + v} \\ M & := M^{-} \cup M^{+} \end{aligned}$

石を打つ直前の盤面と直後の盤面の組により着手を定義している. $M^{-}$ が黒による着手全体の集合, $M^{+}$ が白による着手全体の集合である. $(C^{*}, M)$ は有向グラフになっている。

$M^{-} \cap M^{+} = \emptyset$ である。

$M^{-} \cap M^{+} \neq \emptyset$ とする。このとき、ある $(c, d) \in C^{*} \times C^{*}$ が存在して $(c, d) \in M^{-}$ かつ $(c, d) \in M^{+}$ を満たす。すると、ある $v, w \in N$ が存在して、 $d = c - v = c + w$ を満たす。しかし、明らかに $v \in B_{c - v}$ かつ $v \notin B_{c + w}$ であるからこれは矛盾。

$(c, d) \in M^{-}$ とする。 $d = c - v$ を満たす $v$ はただ一つ存在する。 $(c, d) \in M^{+}$ のときも同様である。

$(c, d) \in M^{-}$ とする。このときある $v \in N$ が存在して $d = c - v$ を満たす。任意の $w \in N ∖ {v}$ に対して $B_{c - v} = B_{c} \cup {v} \neq B_{c} \cup {w} = B_{c - w}$ であるから、 $d = c - v$ を満たす $v \in N$ はただ一つである。

$c \in C^{*}$ 、 $v \in V$ とする。 $c - v \notin C^{*}$ となるとき、 $v$ は $c$ において黒の着手禁止点であるという。また、 $c + v \notin C^{*}$ となるとき、 $v$ は $c$ において白の着手禁止点であるという。

$c - v$ （ $c + v$ ）は黒石（白石）を一つ打ち、取れるなら白石（黒石）を取り上げる、という操作である。もしこの結果が盤面にならないとするなら、 $c$ において黒（白）は $v$ に打つことができない。

盤面と着手の交互列 $r = c_{0} m_{1} c_{1} \dots c_{n - 1} m_{n} c_{n}$ で, 任意の $i = 1, \dots, n$ に対して $m_{i} = (c_{i - 1}, c_{i})$ となるものを着手列という. 着手列全体の集合を $R$ とする.
このとき $c_{0}$ を初期盤面、 $c_{n}$ を最終盤面という。

少しもったいぶった言い方になっているが、「普通に」着手を並べれば着手列となる。

ただし、この定義では黒と白の着手が交互に並んでいる必要はない点に注意されたい。もし黒の着手が連続している場合、その間白はパスをしているものと考える。

$r = c_{0} m_{1} c_{1} \dots c_{n - 1} m_{n} c_{n}$ を着手列とする. 任意の $i, j$ に対して $c_{i} \neq c_{j}$ ならば, $r$ を正規着手列と言う.

これは同一局面の反復を禁ずるもので、いわゆる超劫ルールに相当する。

$(C^{*}, M)$ をグラフとしてみたとき、着手列は歩道に、正規着手列は道にあたる。着手列はその盤面だけ、あるいは着手だけを取り出して並べても一意に定まる。

着手列 $r = c_{1} \dots c_{n}$ 、頂点 $v$ に対して $r (v) := c (v)$ と定める。

これに限らず、着手列 $r$ をその最終盤面そのものであるかのように記号を濫用する。

着手列 $r$ に対して, 得点 $s : R \to R$ を $s (r) = \sum_{v \in V} r (v)$ で定める.

着手列 $r$ の最終盤面において、 $v \in V$ が黒石のとき $r (v) = - 1$ であるから $\sum_{v \in B} r (v) = - | B |$ となる。同様に考えて $\sum_{v \in W} r (v) = | W |$ であり、 $\sum_{v \in N} r (v) = 0$ である。したがって $s (r) = \sum_{v \in V} r (v) = | W | - | B |$ であり、黒石と白石の個数の差を考えていることがわかる。