グラフ碁の死活
この記事では グラフによる碁の表現 を前提としています。
窮極盤面
$c$を配置とする。任意の$v\in N$において$v$が黒または白の着手禁止点であり、$c-v$、$c+v$のうち盤面である方を$d$とおくと、$|l_d(v)|=1$であるとき、$c$を窮極盤面という。
かみ砕いていえば、盤上のすべての石が二眼しか地を持っていない状態のことを指している。窮極盤面において、いわゆるセキの形は存在してないことに注意されたい。
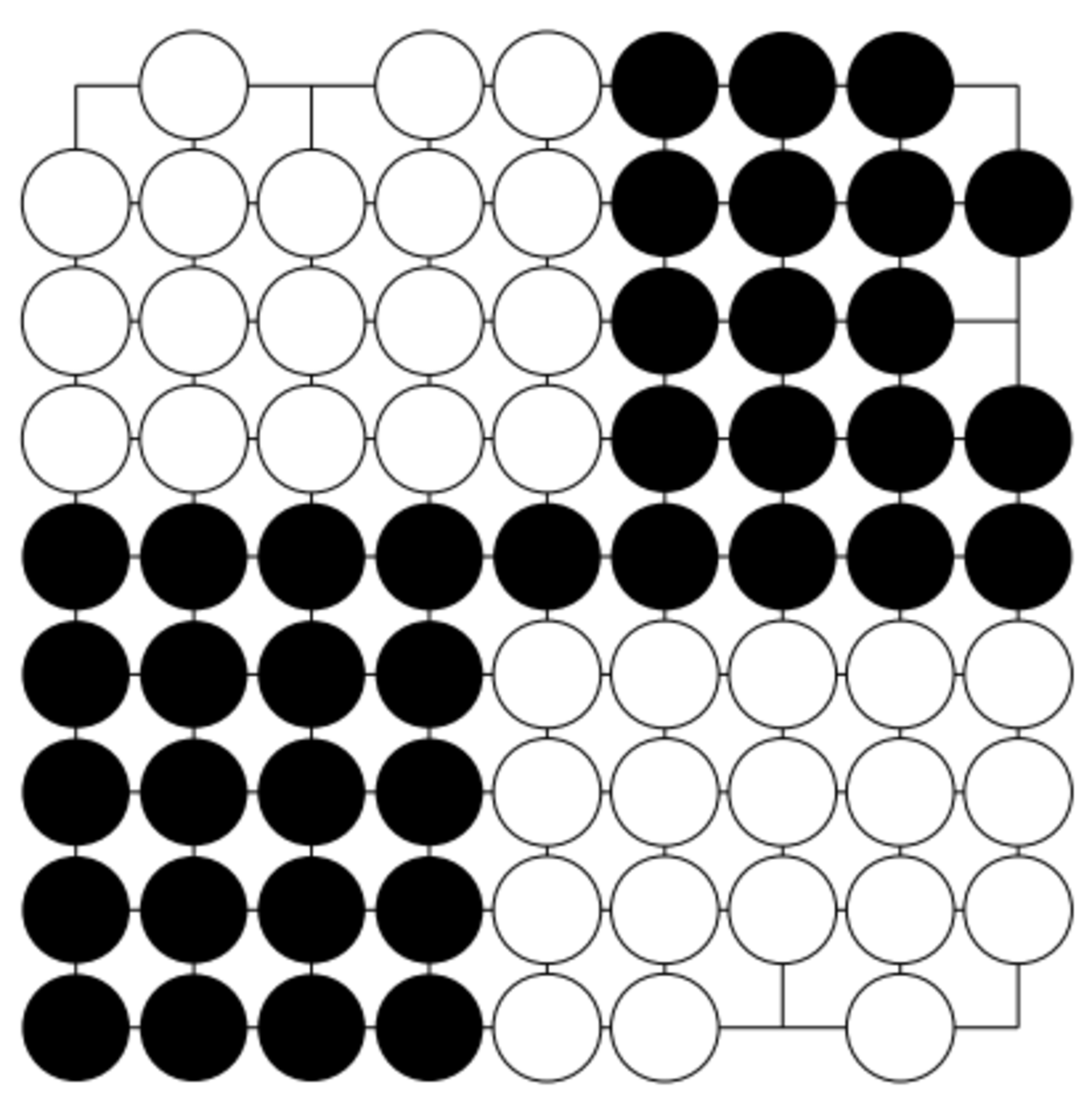窮極盤面の例
窮極盤面における各空点を眼という。黒石に隣接している眼を黒の眼といい、それ全体の集合を$E_B$で表す。同様に白の眼を定め$E_W$と書く。
ある意味逆説的に眼を定義した。普通に使われる眼とは異なり、かなり狭い意味しか持たない。
窮極盤面において、各空点の隣接点は空点でなく、特に一色である。
$c$を窮極盤面、$v\in N$とする。このとき、任意の$w,w'\in\mathrm{Nei}(v)$に対して$c(w)c(w')=1$である。
$c(w)=0$とすると、$v$に打った石は$w$を呼吸点として持つから、$v$は着手禁止点たりえない。よって$c(w)\ne0$であり、同様に$c(w')\ne0$。
したがって$c(w)c(w')$は1または-1である。$c(w)c(w')=-1$と仮定する。$v$を白の着手禁止点、$c(w)=-1$、$c(w')=1$とすると、$l_c(w')=\{v\}$であり、ある$u\in V\setminus\{v\}$が存在して$u\in l(w)$をを満たす。よって、盤面$c-v$において$v$は$u$と$w'$を呼吸点として持つから$|l_{c-v}(v)|>1$である。これは矛盾。$v$が黒の着手禁止点であっても、同様に矛盾が導ける。
以上より$c(w)c(w')=1$である。
さて、窮極盤面において着手しようとすると、自分から一眼になるようにしか打てないわけだが、そうすると相手にその一団が取られてしまう。取り跡に交互に打っていくことを考えれば、再び窮極盤面になったとき元の図よりも自分の石の数は減ることになる。そのため、窮極盤面に至ったら双方これ以上着手しないことが最善となるはずである。
着手列のつながり
着手列$r$において、その最終盤面に着手することで新たな着手列$r'$を作ることができる。そこで、$r$における次の着手列の集合を定義しよう。
まずは、着手列に着手する操作を定義する。
着手列$r=c_0\dots c_n$と着手$m=(c_n,c_n+1)$に対して、以下のように定義する。$$ r+m:= c_0\dots c_nc_{n+1} $$
盤面に石を打つときには、打つ方に合わせて$c-v$か$c+v$と区別していたが、+や-の情報は$m$に内包されていると考えて、黒の着手だろうと白の着手だろうとこの定義では+に統一する。
$r$を正規着手列とする。$r^B$、$r^W$を以下で定義する。また、$r=\{r^B\mid r^W\}$と記す。
\begin{align*}
r^B&:=\{r'\in R\mid r'\mbox{は正規着手列、} \exists m\in M^-\ \mathrm{s.t.}\ r'=r+m\}\\
r^W&:=\{r'\in R\mid r'\mbox{は正規着手列、} \exists m\in M^+\ \mathrm{s.t.}\ r'=r+m\}
\end{align*}
$r^B$は$r$から黒が打つことによって得られる正規着手列全体の集合、$r^W$は$r$から白が打つことによって得られる正規着手列全体の集合である。
グラフ碁の死活
囲碁のルールでよく問題となるのが死活である。グラフ碁を用いて死活問題について考えたい。
前提となるのが、窮極盤面が死活を考えるうえで基準となるということである。すなわち、ある盤面においてその石が活きるか死ぬかというのは、その盤面から着手を続けた結果、どのような窮極盤面に至るかを考えればよいということである。
死活を考える際、その盤面だけを考えればよいように思われるが、同一局面反復の観点から着手列について考える必要がある。
ここで、着手列$r$における頂点$v$の帰結類$o(r,v)$というのを構成しよう。ざっくり言うと、帰結類というのは最終的に$v$の状態がどうなるのかを分類したものになる。
まず、窮極盤面においてはどの石も二眼活きの状態であるから、死活を考える必要がない。ここで帰結類は以下のように定める。ただし、$B,W$は$r$の最終盤面における分割集合である。
$$ o(r,v)=\begin{cases} \mathcal{B}&(v\in B\cup E_B)\\ \mathcal{W}&(v\in W\cup E_W) \end{cases} $$
次に、窮極着手列の直前まで進んだ着手列、つまり$r^B$も$r^W$も窮極着手列からのみ構成されているような着手列を考えよう。
もし、$r^B$の中に$o(r',v)=\mathcal{B}$となる$r'$があれば黒はその着手列を選びたいはずである。同様に$r^W$の中に$o(r',v)=\mathcal{W}$となる$r'$があれば白はその着手列を選ぶだろう。つまり、$r^B$の中に$o(r',v)=\mathcal{B}$となる$r'$があり、$r^W$の中に$o(r',v)=\mathcal{W}$となる$r'$があれば、$v$は次（next）に着手する対局者のものとなるであろう。$r^B$の中に$o(r',v)=\mathcal{B}$となる$r'$があるものの、$r^W$の中に$o(r',v)=\mathcal{W}$となる$r'$がなければ、$v$は必ず黒のものである。逆の場合は白のものになる。
ここで、$r$が窮極着手列の直前まで進んだ着手列のときを考えているから、任意の$r'\in r^B$に対し$o(r',v)=\mathcal{W}$となり、任意の$r'\in r^W$に対し$o(r',v)=\mathcal{W}$となる場合というのは存在しない。しかし、$r$がまだ進んでいない着手列のときを考えると、このような場合は、黒から打つと白のものになり白から打つと黒のものになるので、直前（previous）に着手したほうのものになると考えられる。例えばセキと呼ばれる形がこの場合であり、実際には黒白ともに着手しないことになる。
したがって以下のような表が作れる。各項目がそれぞれの場合の$o(r,v)$の値である。
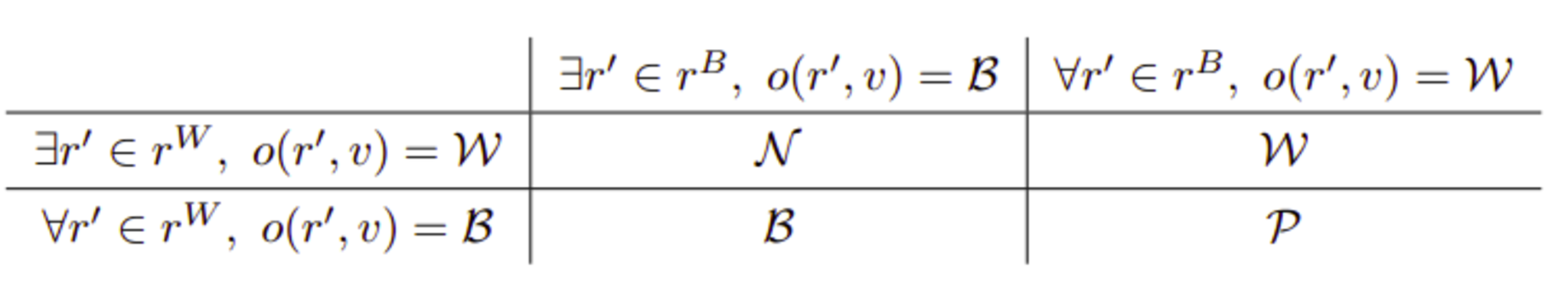帰結類
では、窮極盤面に至るまで複数手以上かかる着手列を考えよう。先に結論を述べると、$o(r,v)$は以下の表のようになる。
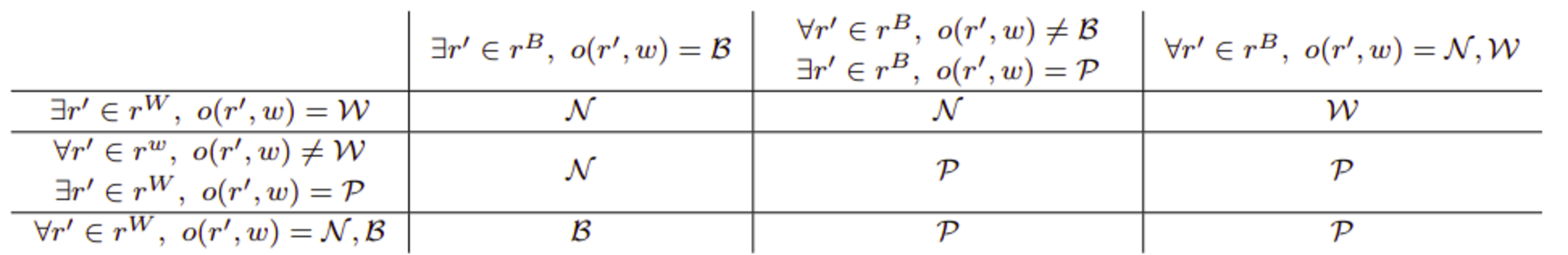帰結類
それぞれの場合について帰結類を考えれる。四隅は窮極着手列の直前まで進んだ着手列のときと同じように考えればよい。$o(r',w)=\mathcal{N}$となるときは次番の対局者のものになり、つまり$r'$を選択した対局者に不利になることに注意しよう。逆に$o(r',w)=\mathcal{P}$となるときは、$r'$を選択する分には問題ないが、囲碁ではパスができるため、そのまま放置されてしまうことが帰結類を考える肝である。
中国式計算法
この節では、純碁式の計算法とは異なる計算法で得点計算する。
中国式と銘打ったのは地石で計算するためであり、半数計算は利用しない。
正規着手列$r$が中国式可終局であるとは、以下の条件を満たすことである。
- $\forall v\in V,\ o(r,v)\ne\mathcal{N}$
- $\forall v\in V,\ \forall w,w'\in [v]_r,\ o(r,w)=o(r,w')$
一つ目の条件は、全ての点が最終的に黒白いづれになるか定まっているか、セキの状態にあれば終局できることを表している。これは直感的にもわかりやすいだろう。
二つ目の条件は、どんな時でも成り立っているように思うかもしれない。しかし、必ず成り立つとは言えない。具体例をあげて見ていこう。
図4は正規着手列$r$によるものとする。この図において、黒白どちらから打っても左下は白のものになるが、右上は黒のものにすることがでる。
例えば抜き跡が図5のようになったとき、白の着手によりこうなるので、次は黒番である。そして、黒が適切に打てば$w$が黒になるように窮極着手列をとることができるので、$o(r,w)=\mathcal{B}$と言いたくなる。
ところが、黒が次にどんな手を打っても、白が適切に対応すれば$v$は白のものになる。つまり$o(r,v)=\mathcal{W}$となる。
以上から、$r$において、$v\sim_rw$であるのに$o(r,v)\ne o(r,w)$となる。
この議論は曖昧な部分を残している。実際には着手列を一手づつのばしながら計算する必要がある。
この盤面でこのまま終局してしまうと、$[v]_r$の石をどう扱うべきかが非常に難しい。そのため、このような同値類が残らない状況で終局するようにする。
一見死に石に見えるが……
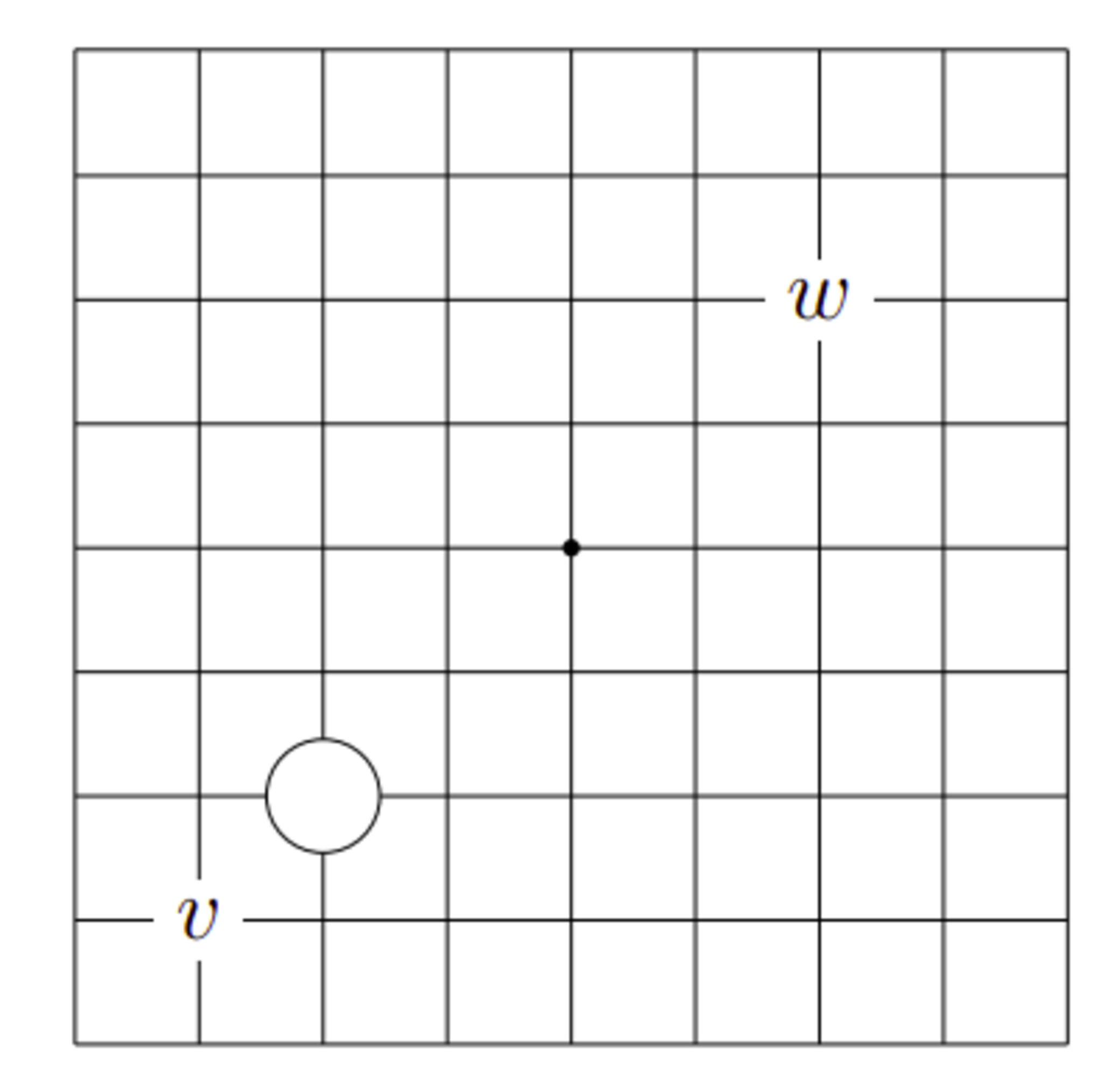抜き跡に活き石が作れる
中国式可終局な着手列$r$の中国式得点$s_c:R\to \mathbb{R}$を\begin{align*} s_c=&|\{v\mid o(r,v)=\mathcal{W}\mbox{または}(o(r,v)=\mathcal{P}\mbox{かつ}r(v)=1)\}|\\ &-|\{v\mid o(r,v)=\mathcal{B}\mbox{または}(o(r,v)=\mathcal{P}\mbox{かつ}r(v)=-1)\}| \end{align*}で定める。$h\in\mathbb{R}$とする。$s_c(r)\ge h$のとき中国式白勝ち、$s_c(r)< h$のとき中国式黒勝ちという。
まず、帰結類が$\mathcal{B}$あるいは$\mathcal{W}$となる点についてはそのままそちらの得点となる。さらに帰結類が$\mathcal{P}$であるような石も持ち主の得点になる。純碁式のときと同様に、$h$はコミである。
可終局であっても終局する必要はないことに気を付けよう。例えば、$\mathcal{P}$の空点を$\mathcal{P}$の自分の石に変えられれば得点は増える。また、切り賃を考えていない点にも注意しよう。こういったことが原因で、中国式得点と、その着手列から自然に導ける窮極着手列の純碁式得点は異なることがある。
