オイラー線を拡張してみた
目次
- はじめに
- オイラー線の復習
- オイラー線を拡張
- おわりに
1.はじめに
みなさんこんにちは!!今回は幾何の勉強をしていてふと思いついた性質があったので紹介していきたいと思います.
必要な前提知識は、複素数に関する計算です.
2.オイラー線の復習
任意の三角形において外心$O$,重心$G$,垂心$H$はこの順で一直線上に並び$|OG|:|GH|=1:2$が成立する.
とても綺麗な定理ですね.今回はこれを拡張してみようという話です.実際に図を描いてみましょう.
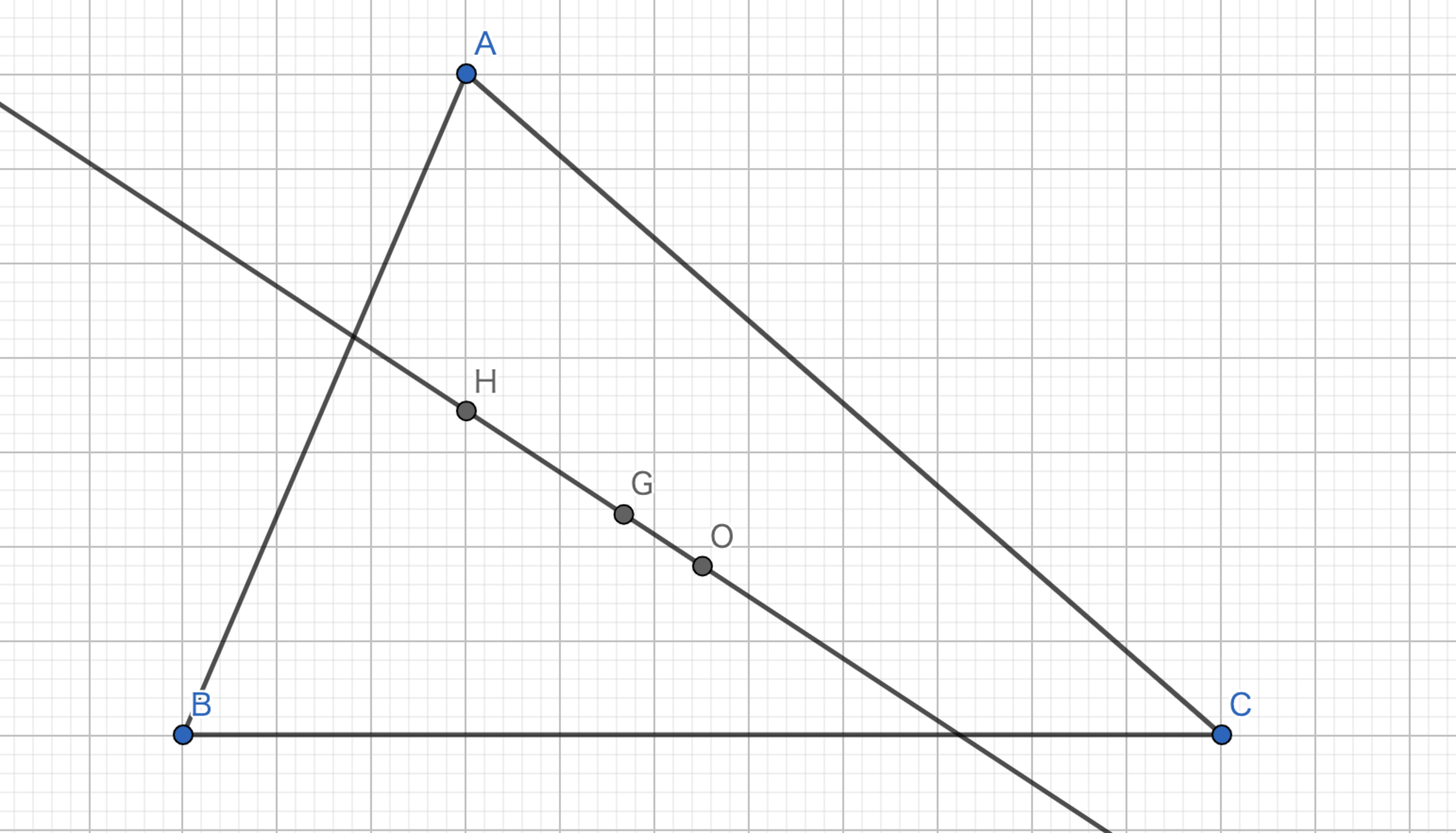 オイラー線
オイラー線
三角形だったらあまり初等的解法と解析的解法で差はないのですが,のちに拡張する際に初等的に示すのは少し大変なので今回は初等的な証明ではなく解析的な証明をします.では,証明を見ていきましょう!
複素平面で考える.三角形ABCの外接円の半径を$1$としても一般性を失わない.外接円の中心$O$の座標を$(0)$.$A,B,C$の座標をそれぞれ$a,b,c$とする.
この時,重心$G$の座標は$\frac{a+b+c}{3}$となる.
$A$から$BC$へと下ろした垂線の式は$z-bc\overline{z}=a-\frac{bc}{a}$となる.
$C$から$AB$へと下ろした垂線の式は$z-ab\overline{z}=c-\frac{ab}{c}$となる.
これらを連立して,$Z=a+b+c$を得る.この時,$O,G,H$は一直線上にあり,$|OG|:|GH|=1:2$が成立する.したがって,題意は示された.
ここでのポイントは,外接円の半径を$1$として複素数の計算を簡略化する点です.うまいこと計算しやすいように立式しましょう.本題へ行きましょう!と言いたいところですが,その前によく使う性質を補題として改めて示しておきます.
円周上の三点$P(p),Q(q),R(r)$が成す三角形$PQR$の垂心の座標は$p+q+r$となる
$P$から$QR$に降ろした垂線の方程式は$z-qr\overline{z}=p-\frac{qr}{p}$となる.
$Q$から$RP$に降ろした垂線の方程式は$z-rp\overline{z}=q-\frac{rp}{q}$となる.
上記の二式を連立して解くと$Z=p+q+r$となる.したがって,題意は示されてた.
3.オイラー線の拡張
円に内接する$n$角形$A_{1}A_{2}\cdots A_{n}$の重心を$G$,外心を$O$,三角形$A_{1}A_{2}A_{3},A_{2}A_{3}A_{4},\cdots,A_{n}A_{1}A_{2}$の垂心を$H_{1},H_{2},\cdots,H_{n}$とする.$n$角形$H_{1},H_{2},\cdots,H_{n}$の重心を$G'$とすると以下が成り立つ.
$O,G,G'$は一直線上に並び,$|OG|:|GG'|=1:2$となる.
う〜ん厳ついですね.でも証明はそこまで難しくないです.見ていきましょう!
複素平面で考える.$n$角形$A_{1}A_{2}\cdots A_{n}$の外接円の半径を$1$としても一般性を失わない.外接円の中心$O$の座標を$(0)$.$A_{i}$の座標を$(a_{i})$とする.(以下,添字は$n$を法とする.)
この時,重心$G$の座標は$\frac{1}{n}\left(A_{1}+A_{2}+\cdot+A_{n}\right)$となる.
補題$2$より,$H_{n}=A_{n}+A_{n+1}+A_{n+2}$となる.それらの重心$G'$は以下のように計算できる.
$$
\frac{1}{n}\sum_{i=1}^{n}H_{i}=\frac{1}{n}\sum_{i=1}^{n}(A_{i}+A_{i+1}+A_{i+2})=\frac{3}{n}\left(A_{1}+A_{2}+\cdots+A_{n}\right)
$$
したがって,$O,G,G'$は一直線上に存在し,$|OG|:|GG'|=1:2$が成立する.これより,題意は示された.
4.おわりに
実は,今回の拡張は複素数で幾何を解く練習をしていた時に思いついたものです.その際に,とてもお世話になったnatuさんのMathlogの リンク を置いておきます.神コンテンツなので興味がある人は是非みてみてください!
今回も,記事を見ていただいてありがとうございました!!
