13
高校数学解説
レムニスケートと1本の直線が生み出す関係について - A relationship between a line and a lemniscate -
613
0
$$$$
いつも通り長めの数式が出てくるので、横スクロール1000本ノックをしてからお読みください。
前回の記事
に引き続き、レムニスケートに関する研究の成果を掲載する。いつも引き続いているよなこの人。「レムニスケートって何だよ、メチルフェニデートの仲間か？」という方は先述した前回の記事を参照しよう。
さて、レムニスケートは1694年にベルヌーイが発見して以来、ファニャーノやオイラーといった数学者によって代数的に研究されてきた4次曲線であるが……といういかにも論文らしい書き出しをすると喀血する病にかかっているので、簡潔に発見した性質とその証明だけを述べることにする。
なお、今回も先行研究が見つからなかったので、取り敢えず『今後の活躍をお祈りする定理 ~ Il teorema del fallimento della ricerca di lavoro ~ 』(仮)と名付けておく。先行研究をご存知の方、あるいはネーミングセンスに遺憾の意を表明したい方はコメントまで。
さて、レムニスケートは1694年にベルヌーイが発見して以来、ファニャーノやオイラーといった数学者によって代数的に研究されてきた4次曲線であるが……といういかにも論文らしい書き出しをすると喀血する病にかかっているので、簡潔に発見した性質とその証明だけを述べることにする。
なお、今回も先行研究が見つからなかったので、取り敢えず『今後の活躍をお祈りする定理 ~ Il teorema del fallimento della ricerca di lavoro ~ 』(仮)と名付けておく。先行研究をご存知の方、あるいはネーミングセンスに遺憾の意を表明したい方はコメントまで。
こちら側で定理名の暫定案を出したものの、実際は好きに呼称していただいて構わない。例えばピタゴラスが「この定理を三平方の定理と呼べ」と言った事実は明らかになっていないが、我々は勝手にピタゴラスの発見した定理を三平方の定理と呼んでいる。定理名は、それくらいのフレキシビリティがあって然るべきものだ。
定理(仮)の紹介
レムニスケート$\Lambda$の中心を$O$とする。ある直線と$\Lambda$が4点$A,B,C,D$で交わっており、$\triangle OAB,$$\triangle OCD$の外接円の半径がそれぞれ$x,y$であるとき、$\Lambda$に囲まれる領域の面積は$2xy$である。
頼んだぞ、自動翻訳
レムニスケート$\Lambda$と4点で交わっている限り、直線はどこに引いてもよい。加えて、定理を認めれば自明な系として、$\triangle OAD$と$\triangle OBC$の外接円の半径の積も$xy$となることが挙げられる。本定理の威力・汎用性が伝わるだろうか。
ちなみに、巷ではレムニスケートサイン${\rm sl}\left(\theta\right)$(${\rm sleaf}_2 \left(\theta\right)$とも表記する)やレムニスケートコサイン${\rm cl}\left(\theta\right)$(${\rm cleaf}_2 \left(\theta\right)$とも表記する)といった特殊な関数が存在するそうで、これらの関数の存在によって幾人もの数学者がレムニスケートの弧長に関する微分積分学的研究を発表している。だが本定理のように、レムニスケートの弧長が直接関係しない領域については未開拓な部分が多いようだ。あ、本定理はただの座標計算で証明できるため${\rm sl}\left(\theta\right)$や${\rm cl}\left(\theta\right)$の出る幕は無いよ。出てこないなら書くな。
ちなみに、巷ではレムニスケートサイン${\rm sl}\left(\theta\right)$(${\rm sleaf}_2 \left(\theta\right)$とも表記する)やレムニスケートコサイン${\rm cl}\left(\theta\right)$(${\rm cleaf}_2 \left(\theta\right)$とも表記する)といった特殊な関数が存在するそうで、これらの関数の存在によって幾人もの数学者がレムニスケートの弧長に関する微分積分学的研究を発表している。だが本定理のように、レムニスケートの弧長が直接関係しない領域については未開拓な部分が多いようだ。あ、本定理はただの座標計算で証明できるため${\rm sl}\left(\theta\right)$や${\rm cl}\left(\theta\right)$の出る幕は無いよ。
90％が行間で構成された証明 (2022.06.14 行間を少し埋めました)
$xy$座標平面上のレムニスケート$\lambda$、円$\gamma_1,\gamma_2$および直線$l$を、実数$c\geq 0,d>0$を用いて以下のように定義しておく。
$$ \begin{eqnarray} \lambda&:&\left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right) \\[6pt] \gamma_1&:&d\left(x^{2}+y^{2}\right)-2\left(cx+y\right)=0 \\[6pt] \gamma_2&:&\left(c^{2}+1\right)\left(x^{2}+y^{2}\right)+2d\left(cx-y\right)=0 \\[6pt] l&:&c\left(c^{2}-d^{2}+1\right)x+\left(c^{2}+d^{2}+1\right)y+\left(c^{2}-1\right)d=0 \end{eqnarray}$$
$\lambda$について、本定理の成立を確認すればよい($\lambda$の面積が$2$であることの証明は省くので、各自文献等で調べてほしい)。すなわち、$\lambda$と$l$が4つの交点$A',B',C',D'$をもつ場合に、$\triangle OA'B'$の外接円の半径と$\triangle OC'D'$の外接円の半径の積が$1$になることを全力で示しにかかる($\because $ $\lambda$の面積は$2$)。
$$ \begin{eqnarray} \lambda&:&\left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right) \\[6pt] \gamma_1&:&d\left(x^{2}+y^{2}\right)-2\left(cx+y\right)=0 \\[6pt] \gamma_2&:&\left(c^{2}+1\right)\left(x^{2}+y^{2}\right)+2d\left(cx-y\right)=0 \\[6pt] l&:&c\left(c^{2}-d^{2}+1\right)x+\left(c^{2}+d^{2}+1\right)y+\left(c^{2}-1\right)d=0 \end{eqnarray}$$
$\lambda$について、本定理の成立を確認すればよい($\lambda$の面積が$2$であることの証明は省くので、各自文献等で調べてほしい)。すなわち、$\lambda$と$l$が4つの交点$A',B',C',D'$をもつ場合に、$\triangle OA'B'$の外接円の半径と$\triangle OC'D'$の外接円の半径の積が$1$になることを全力で示しにかかる($\because $ $\lambda$の面積は$2$)。
まず、$\gamma_1$の中心$\left(\dfrac{c}{d},\dfrac{1}{d}\right)$は、$c,d$の値を変化させると第1象限全体および$y$軸の正の部分を動く(この領域を$S$とする)。この事実から、上で設定した条件の十分性が保証される。というのも、「$\lambda$と$l$の4つの交点のうち2つと$\lambda$の中心を通る円」の中心$O_1$は明らかに第1象限～第4象限のいずれか(もしくは原点を除く$y$軸上)にあり、$x$軸、$y$軸に関する対称移動を適切に行えば、必ず$S$の範囲内に$O_1$を位置させられるためである。
$\lambda$と$l$が4つの交点$A',B',C',D'$をもつとき、$A'$の座標を$(a,b)$とすると、以下の式が成立する(これは$A'$について考えた場合であるが、他の交点についても同様の方程式を立てられることに注意せよ)。
$$ \begin{eqnarray} \left\{ \begin{array}{ll} &\!\!\!\! \left(a^{2}+b^{2}\right)^{2}=2\left(a^{2}-b^{2}\right) &\dots(P) \\[6pt] &\!\!\!\! c\left(c^{2}-d^{2}+1\right)a+\left(c^{2}+d^{2}+1\right)b+\left(c^{2}-1\right)d=0 &\dots(Q) \end{array} \right. \end{eqnarray}$$ $(P)$と$(Q)$を連立して解けば、$A'$の座標が求められる。$B',C',D'$の座標も求めて、外接円の方程式まで導出してしまおう。$(Q)$を$b=$〇〇〇という形に変形する。それを$(P)$に代入して$b$を消去。かくして現れたのは$a$に関する4次方程式。
……4次方程式？？？？
と、ここに至って「ダイレクトに座標計算」作戦の雲行きが一気に怪しくなる。実際、そうやって得た4次方程式は非常に複雑な解をもち、正直に言えば書きたくない。仮に書いても愛すべき読者からのブラウザバックを受けるだけであろう。レッツ方針転換。
$$ \begin{eqnarray} \left\{ \begin{array}{ll} &\!\!\!\! \left(a^{2}+b^{2}\right)^{2}=2\left(a^{2}-b^{2}\right) &\dots(P) \\[6pt] &\!\!\!\! c\left(c^{2}-d^{2}+1\right)a+\left(c^{2}+d^{2}+1\right)b+\left(c^{2}-1\right)d=0 &\dots(Q) \end{array} \right. \end{eqnarray}$$ $(P)$と$(Q)$を連立して解けば、$A'$の座標が求められる。$B',C',D'$の座標も求めて、外接円の方程式まで導出してしまおう。$(Q)$を$b=$〇〇〇という形に変形する。それを$(P)$に代入して$b$を消去。かくして現れたのは$a$に関する4次方程式。
……4次方程式？？？？
と、ここに至って「ダイレクトに座標計算」作戦の雲行きが一気に怪しくなる。実際、そうやって得た4次方程式は非常に複雑な解をもち、正直に言えば書きたくない。仮に書いても愛すべき読者からのブラウザバックを受けるだけであろう。レッツ方針転換。
折角最初に$\gamma_1$と$\gamma_2$の式も定義したのだから、積極的に使っていこう。要するに、これらの式に$x=a,y=b$を代入し、ついでに掛け合わせてみる。
$$ \left(d\left(a^{2}+b^{2}\right)-2\left(ca+b\right)\right)\left(\left(c^{2}+1\right)\left(a^{2}+b^{2}\right)+2d\left(ca-b\right)\right)$$ これを以下のように変形していく($(P)$および$(Q)$を適宜用いた)。
$$ \begin{array}{l} \left(d\left(a^{2}+b^{2}\right)-2\left(ca+b\right)\right)\left(\left(c^{2}+1\right)\left(a^{2}+b^{2}\right)+2d\left(ca-b\right)\right) \\[6pt] \qquad=\left(c^{2}+1\right)d\left(a^{2}+b^{2}\right)^{2}+2\left(d^{2}\left(ca-b\right)-\left(c^{2}+1\right)\left(ca+b\right)\right)\left(a^{2}+b^{2}\right)-4d\left(c^{2}a^{2}-b^{2}\right) \\[6pt] \qquad=2\left(\left(c^{2}+1\right)d\left(a^{2}-b^{2}\right)+\left(d^{2}\left(ca-b\right)-\left(c^{2}+1\right)\left(ca+b\right)\right)\left(a^{2}+b^{2}\right)-2d\left(c^{2}a^{2}-b^{2}\right)\right) \\[6pt] \qquad=-2\left(a^{2}+b^{2}\right)\left(c\left(c^{2}-d^{2}+1\right)a+\left(c^{2}+d^{2}+1\right)b+\left(c^{2}-1\right)d\right) \\[6pt] \qquad=0 \end{array}$$ 計算結果が$0$になった。すごい。奇跡。いやまあそうなるように定義したんですがね。
$$ \left(d\left(a^{2}+b^{2}\right)-2\left(ca+b\right)\right)\left(\left(c^{2}+1\right)\left(a^{2}+b^{2}\right)+2d\left(ca-b\right)\right)$$ これを以下のように変形していく($(P)$および$(Q)$を適宜用いた)。
$$ \begin{array}{l} \left(d\left(a^{2}+b^{2}\right)-2\left(ca+b\right)\right)\left(\left(c^{2}+1\right)\left(a^{2}+b^{2}\right)+2d\left(ca-b\right)\right) \\[6pt] \qquad=\left(c^{2}+1\right)d\left(a^{2}+b^{2}\right)^{2}+2\left(d^{2}\left(ca-b\right)-\left(c^{2}+1\right)\left(ca+b\right)\right)\left(a^{2}+b^{2}\right)-4d\left(c^{2}a^{2}-b^{2}\right) \\[6pt] \qquad=2\left(\left(c^{2}+1\right)d\left(a^{2}-b^{2}\right)+\left(d^{2}\left(ca-b\right)-\left(c^{2}+1\right)\left(ca+b\right)\right)\left(a^{2}+b^{2}\right)-2d\left(c^{2}a^{2}-b^{2}\right)\right) \\[6pt] \qquad=-2\left(a^{2}+b^{2}\right)\left(c\left(c^{2}-d^{2}+1\right)a+\left(c^{2}+d^{2}+1\right)b+\left(c^{2}-1\right)d\right) \\[6pt] \qquad=0 \end{array}$$ 計算結果が$0$になった。すごい。奇跡。
したがって、$A'$は$\gamma_1$または$\gamma_2$の周上にあるといえる。同様に、$B',C',D'$も$\gamma_1$または$\gamma_2$の周上にある。これら4点は同一直線上に存在するので、$\gamma_1$と$\gamma_2$の周上にそれぞれ2つずつ交点が乗っていることが判る。$\gamma_1$と$\gamma_2$が本定理に登場する外接円そのものだったわけだ。
あとはただの掛け算。$\gamma_1$の半径は$\dfrac{\sqrt{\displaystyle c^2+1}}{d}$、$\gamma_2$の半径は$\dfrac{d}{\sqrt{\displaystyle c^2+1}}$であり、これらの積は$1$であるから示された。 (証明終)
あとはただの掛け算。$\gamma_1$の半径は$\dfrac{\sqrt{\displaystyle c^2+1}}{d}$、$\gamma_2$の半径は$\dfrac{d}{\sqrt{\displaystyle c^2+1}}$であり、これらの積は$1$であるから示された。 (証明終)
定理(仮)から得られる系の例
2点$F,F'$を焦点にもつレムニスケート$\Lambda$の中心を$O$とする。$\Lambda$の周上にとった2点$P,Q$が$PQ \parallel OF'$をみたすならば、$\triangle OPQ$の外接円の半径は$OF'$と一致する。
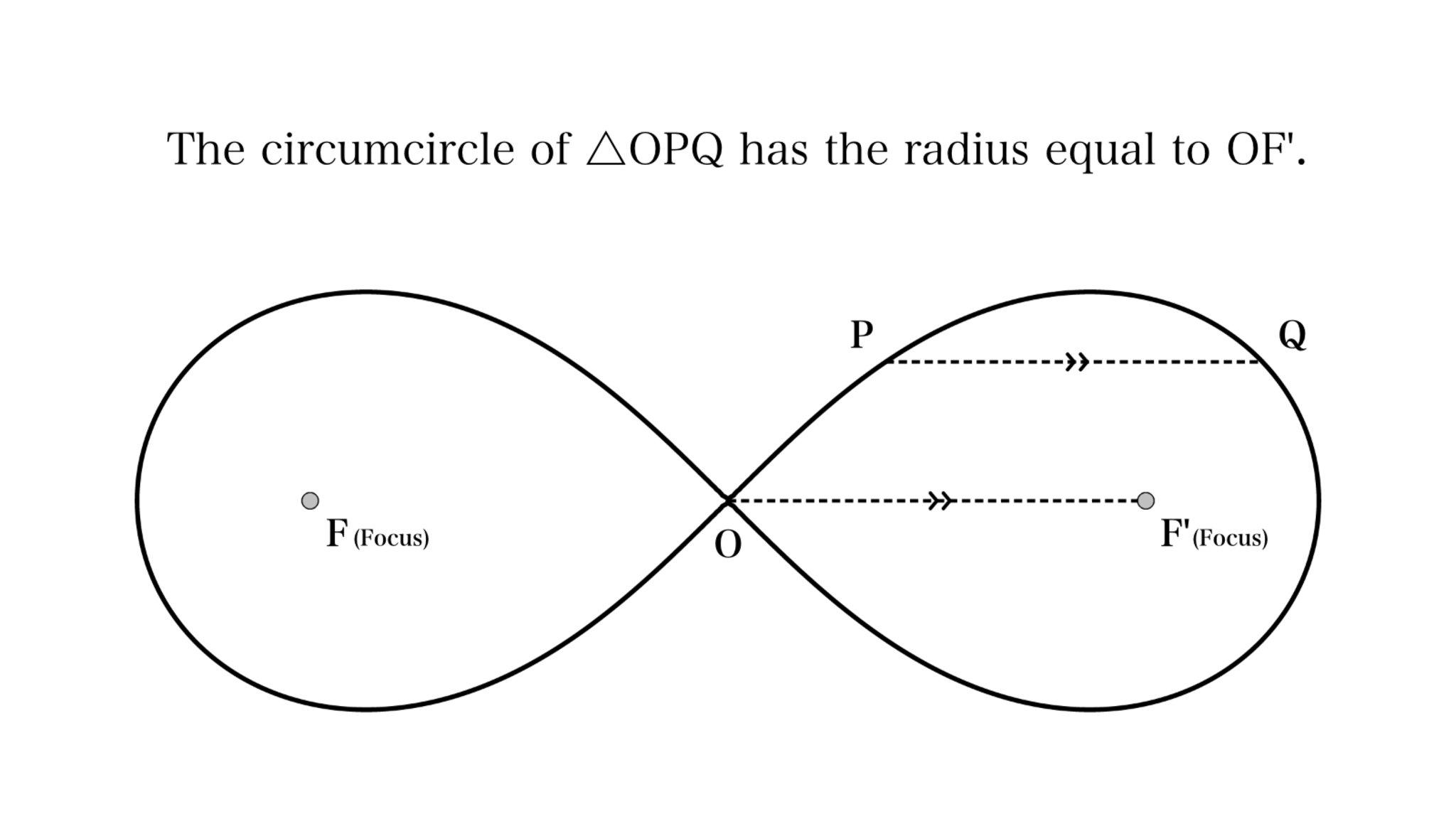線分PQの位置は任意である
証明は読者に任せることとする。定理を使えそうな形にするべく、補助線を引いてみよう。
以下、お気持ち表明となります
もしも上の証明の行間を読み取れなかった方がいれば、証明に登場した4つの方程式を
Dから始まるグラフ計算機
に打ち込むと、流れを理解しやすくなるであろう。よく分からない方程式はひとまずグラフを確認すること、これは高校範囲までの数学を理解するうえで重要な習慣といえる。
余談として、私はこれらの方程式を探すのに3日かけた。ゆえに、3日以内に証明を読み切れた読者は私より賢い。
(何のために3日もかかったのか……、それは、出来るだけ簡単で美しい設定を追求したこと、および Wから始まる計算知能 がレムニスケートと直線の交点を求めてくれなかったことに起因する。いくら計算知能さんといっても2元4次の連立方程式は厳しすぎたか。)
余談として、私はこれらの方程式を探すのに3日かけた。ゆえに、3日以内に証明を読み切れた読者は私より賢い。
(何のために3日もかかったのか……、それは、出来るだけ簡単で美しい設定を追求したこと、および Wから始まる計算知能 がレムニスケートと直線の交点を求めてくれなかったことに起因する。いくら計算知能さんといっても2元4次の連立方程式は厳しすぎたか。)
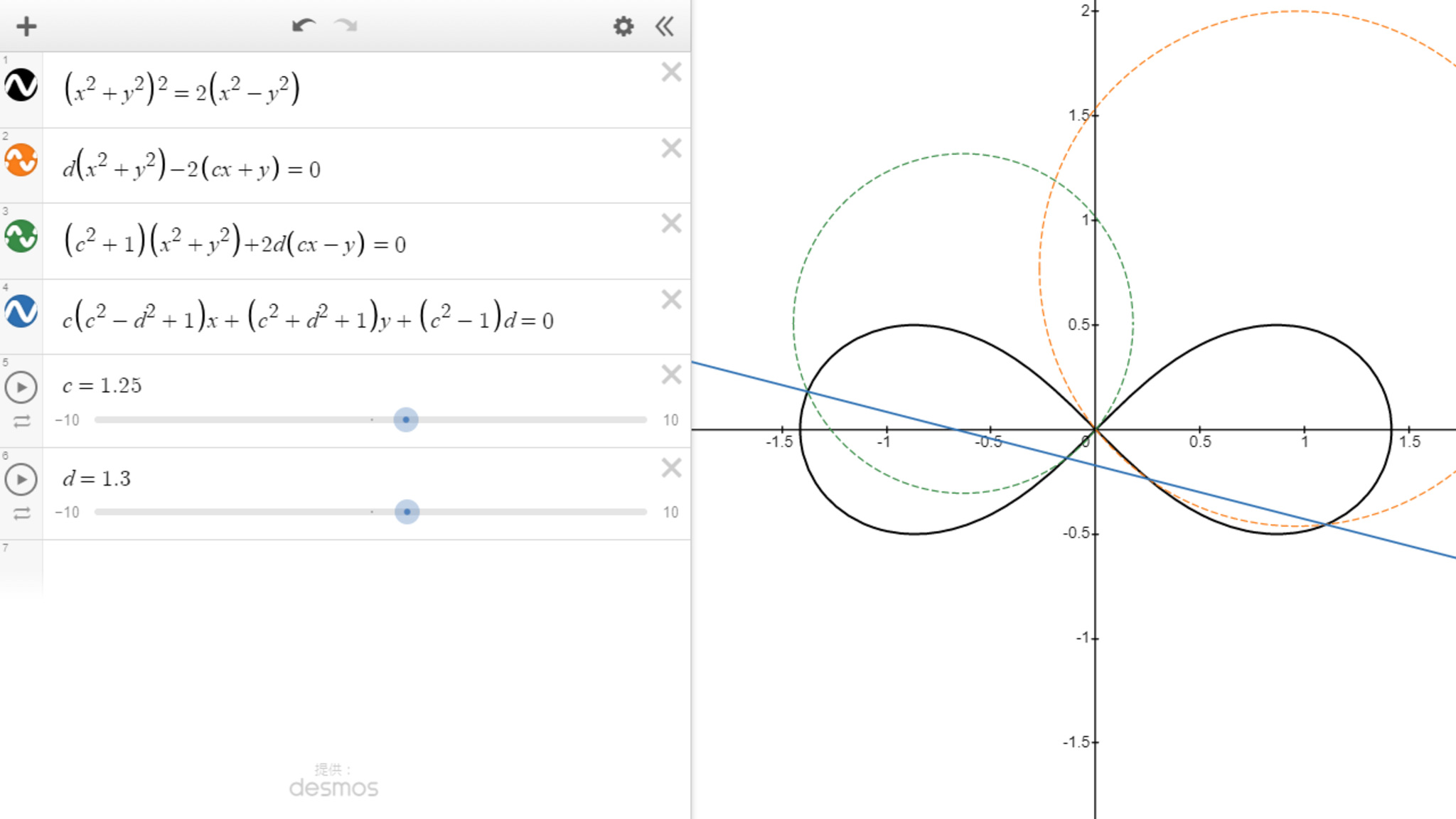方程式の探索が本当に大変だった
ところで。私の本音としては、本定理が既出であってほしいという願いが大きい。ここまで読めばお分かりのはずであるが、この性質はあまりにもシンプルで、少しでもレムニスケートの幾何学的研究をした人ならば見つけられて当然、と言わんばかり。それが仮に新出であった場合、私は人類全体におけるレムニスケート研究への怠慢を感じずにいられない。ベルヌーイがレムニスケートを発見してからの約330年、我々は何をしてきたのか。直線との交点さえ考察してこなかったのか。そういう疑問に駆られてしまうからだ。……これ以上書くと本当に既出だったときに生涯消えない恥辱を背負うことになりそうなので、ここで愚考を止めておくことにする。
投稿日：2022年6月12日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中