パッポス・ギュルダンの定理
パッポス・ギュルダンの定理
今回は知っているととても便利なパッポス・ギュルダンの定理について、証明と利用の仕方について説明していきたいと思います。
左図のような物体を、ある軸について回転させた時の回転体の体積Vは
V = 2πL×S
と表すことができる
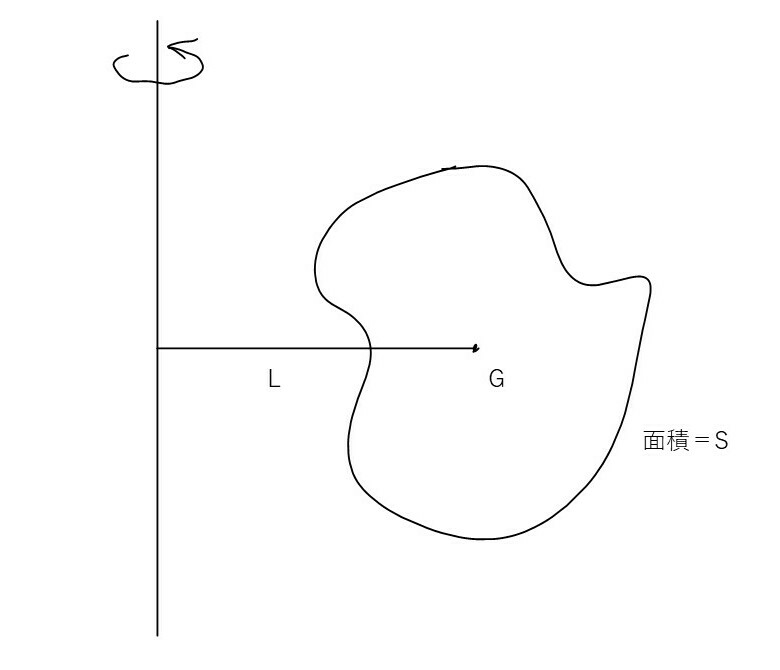 図1
図1
非常に簡単な形で表されることが魅力的ですね!
しかし証明ともなるとなかなか複雑になってきます。特に高校生だと理解しがたいかもしれません。ゆっくり理解していきましょう。証明に必要となってくるのは2つの要素です。
重心の位置を求める
まずは重心の位置から求めていきましょう。上図にあるとおり、重心の座標は軸からの距離、(x座標)しか使わないので重心のx座標を考えていきます。そこで物理では、下図のような6つの質点からなる物体の重心のx座標Gxは以下のように表されます。
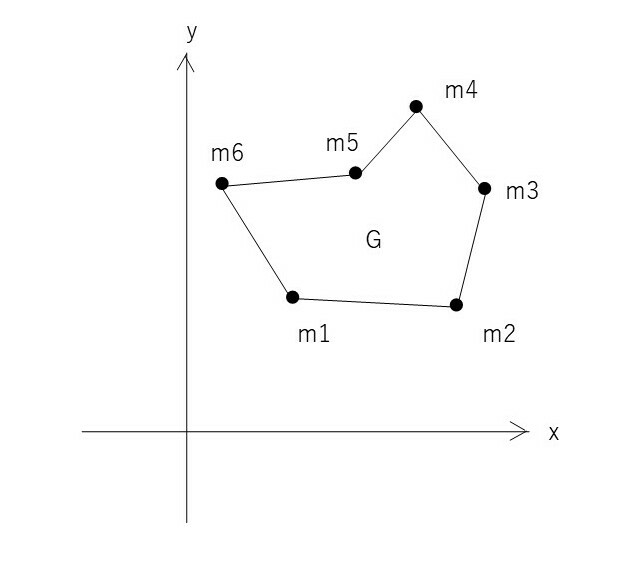 図2
図2
$$ Gx=\frac{x_1m_1+x_2m_2+x_3m_3+x_4m_4+x_5m_5+x_6m_6}{m_1+m_2+m_3+m_4+m_5+m_6} $$
要するに、分母は物体全体の質量、分子は微小質量に距離をかけたものの合計となっているわけです。これを考えながら今回に当てはめていきましょう。
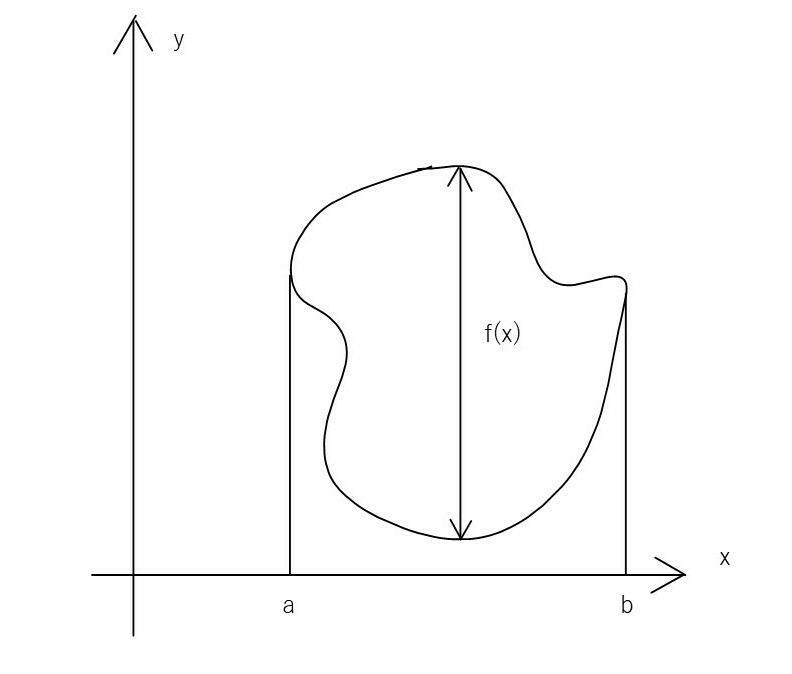 図3
図3
上図は今回y軸に関して回転させる物体であり、関数f(x)は物体のy軸方向の長さを表しています。また、物体のx軸方向の長さは図の通りb-aとなります。これに関して先ほどのポイントと照らし合わせて重心のx座標を求めていきます。
今回はx方向の実なので、厚み(画面に垂直な方向)は無視して考えます。納得しがたいという人は、厚み1と考えるといいでしょう。また、物体の密度をρとします。すると微小質量はf(x)dxとなり、質量は
$$
\int_{a}^{b}ρf(x)dx
$$と表すことができます。また、分子は(x座標×微小質量)の合計であるため、
$$
\int_{a}^{b}xρf(x)dx
$$と表すことができます。ゆえに求めるべき重心のx座標 Gxは、
$$
G_x= \frac{\int_{a}^{b}xρf(x)dx}{\int_{a}^{b}ρf(x)dx}
= \frac{\int_{a}^{b}xf(x)dx}{\int_{a}^{b}f(x)dx}
$$となります。そこで、この式の分母は物体の微小長さの合計となっているため、これは面積です。ゆえに
$$
G_x=\frac{\int_{a}^{b}xf(x)dx}{S}
$$という形で表すことができます。これで重心のx座標を求めることができましたね。次のポイントに移りましょう。
バウムクーヘン積分
次にバウムクーヘン積分について説明します。と言ってもここまで説明するとかなり長くなってしまうので簡単にしておきます。
下図のような、連続関数f(x)とx軸、x=a,x=bで囲まれた範囲をy軸に関して回転させた時にできる部分の体積Vは
$$
\int_{a}^{b}2πxf(x)dx
$$
と表すことができる。
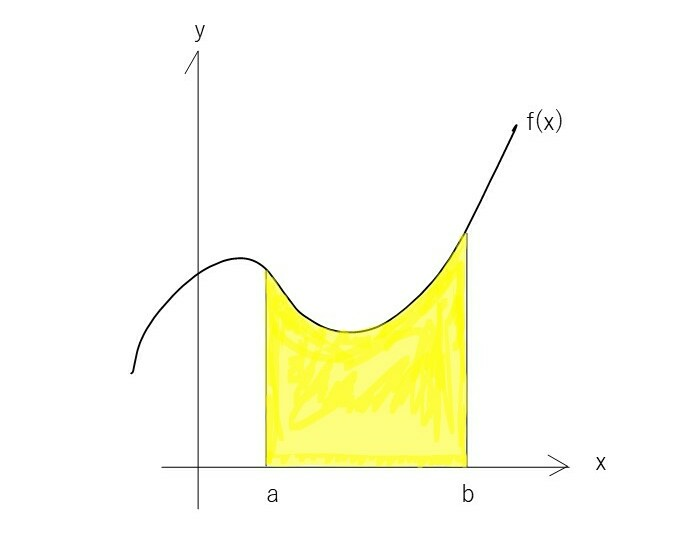 図4
図4
f(x)dxというのは、微小部分xに対しての面積ですね。それにy軸からの距離xと2πがかけられています。つまり、積分の中身は微小部分xに対する、y軸で回転させた時の円筒の側面積を表しています。2πxf(x)で円筒の側面積、それにdxという厚みをかけて[a,b]の範囲で積分することで体積を求めているのです。
これで材料がそろいました。先ほどの重心より、
$$
LS= \int_{a}^{b}xf(x)dx
$$
であり、これをバウムクーヘン積分の公式に代入すれば、
$$
V=2πLS
$$
と、証明することができました。
ここで注意があります。パッポス・ギュルダンの定理は回転軸に回転対象が重なっていた場合適用できません。そこだけはチェックしておきましょう。
いかがだったでしょうか。簡単な定理でも証明するとなってくるとなかなか難しいものです。でも証明を理解してしまえば、後ろめたさがなく定理を利用することができます。ぜひともほかの定理でも証明を大事にしてください。また、この定理の証明ではバウムクーヘン積分をするため高校の範囲外です。大学入試ではおそらくご法度となるでしょう。しっかりと定石で計算して、検算で利用するようにしましょう。
