日曜数学会発表資料「1の19乗根を求めてみた話」

はじめに

　この記事では私、子葉が6/19(日)に開催された第24回日曜数学会にて発表した内容をそれとなーくまとめたものになります(発表の一部始終については ここ で見れます)。全体的には私が前に書いた記事「 1の冪根をたくさん求めてみた(解説付き) 」の内容を発表用に凝縮したものになってます。

なんでそんなん求めたの？

スライド1
　どうも、子葉と申します。今回は「$1$の$19$乗根を求めてみた話」という話をさせていただきますが、まず「なんでそんなもの求めたのか」という話をしておきます。

スライド2
　初めは高校生の頃、僕が数学にハマり始めたころですね。色々な数学の話を調べてたらこんな話がありました。

これを初めて知った当時はやはり「すげー！」と思いました。

スライド3
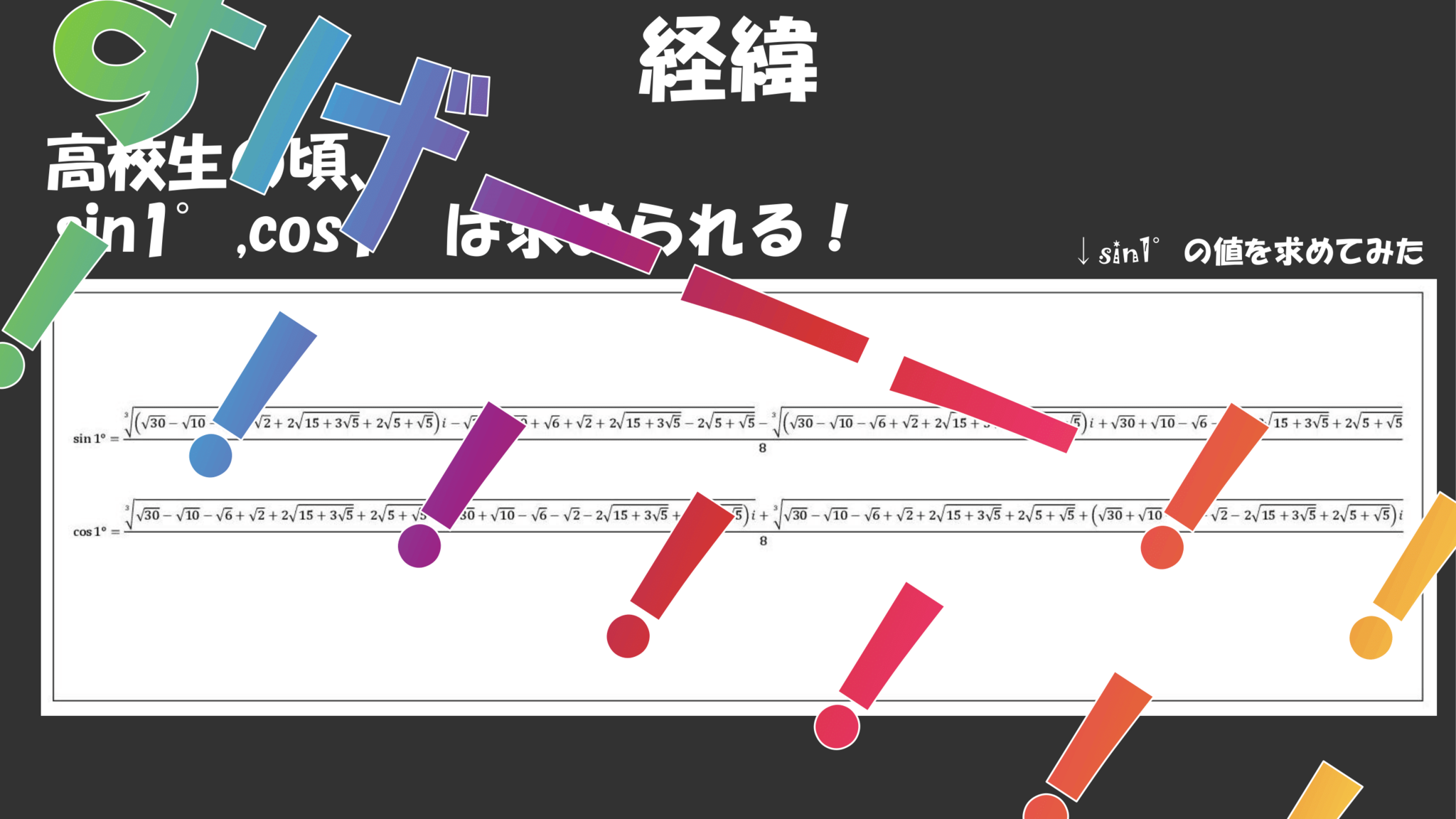
　そしてこれを掘り下げていくと「 $\sin1^\circ$の値を求めてみた 」という記事を見つけ、そこには「$\sin1^\circ,\cos1^\circ$は具体的にこう求められる！」と書いてあり、

スライド4
と感じました。レインボーすげーです。激ヤバ。

スライド5
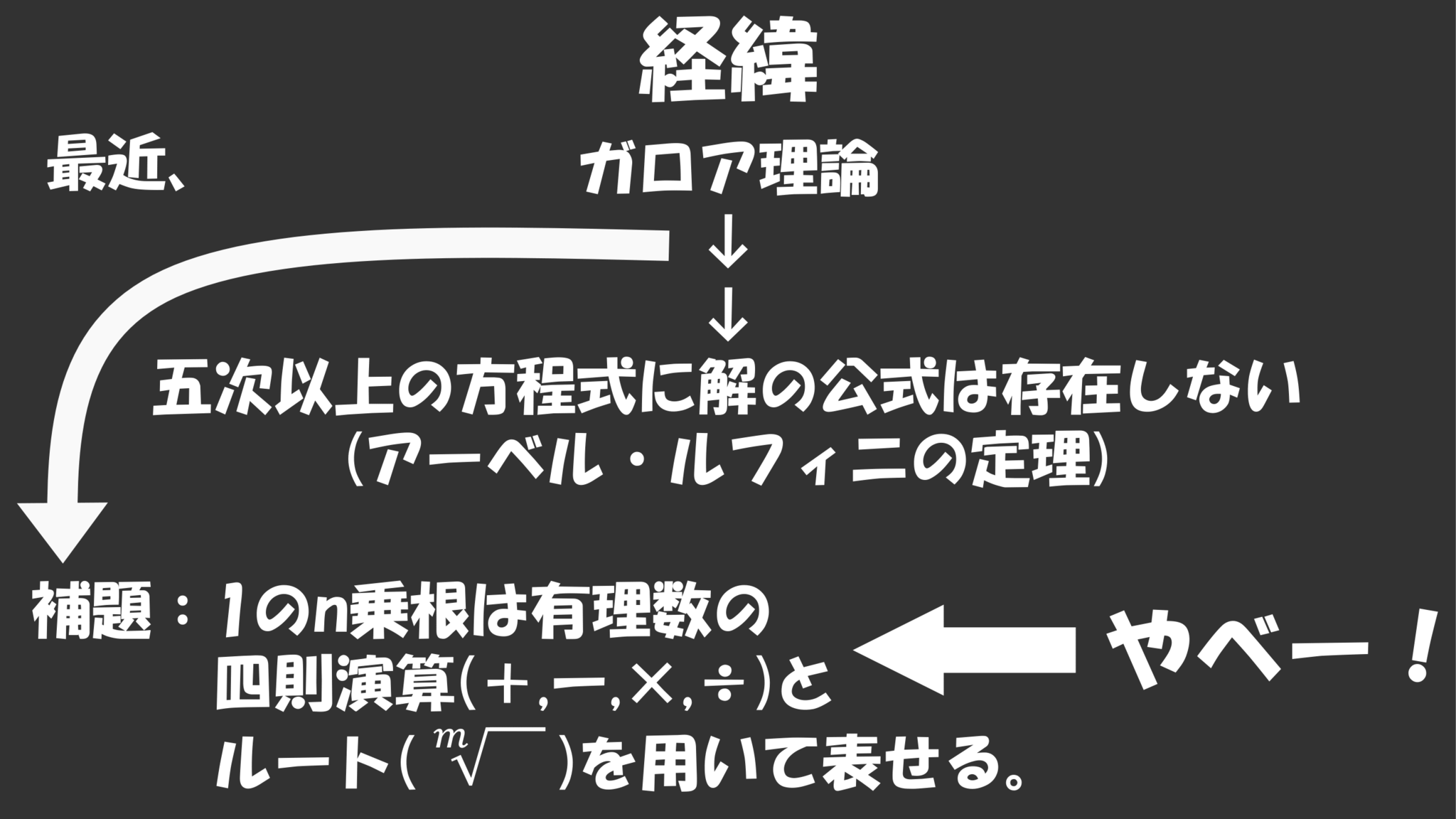
　高校生の頃はそれ以上深掘りをすることはなかったのですが、最近ガロア理論の「五次以上の方程式に解の公式は存在しない」という話を復習してた際にこんな補題を見かけました。

初めて勉強してた時にはガロア理論がよくわかってなかったので素通りしてましたが、あらためて見てみると「やべー！」と感じました。

スライド6
　そして調べてみると ある文献 に「実際$1$の$11,13,17$乗根(素数乗根が重要)の実部は具体的にこのように求めることができる。」と書いてあり、

スライド7
となりました。レインボーどひゃーです。感無量。

どうやって求めるの？

スライド8
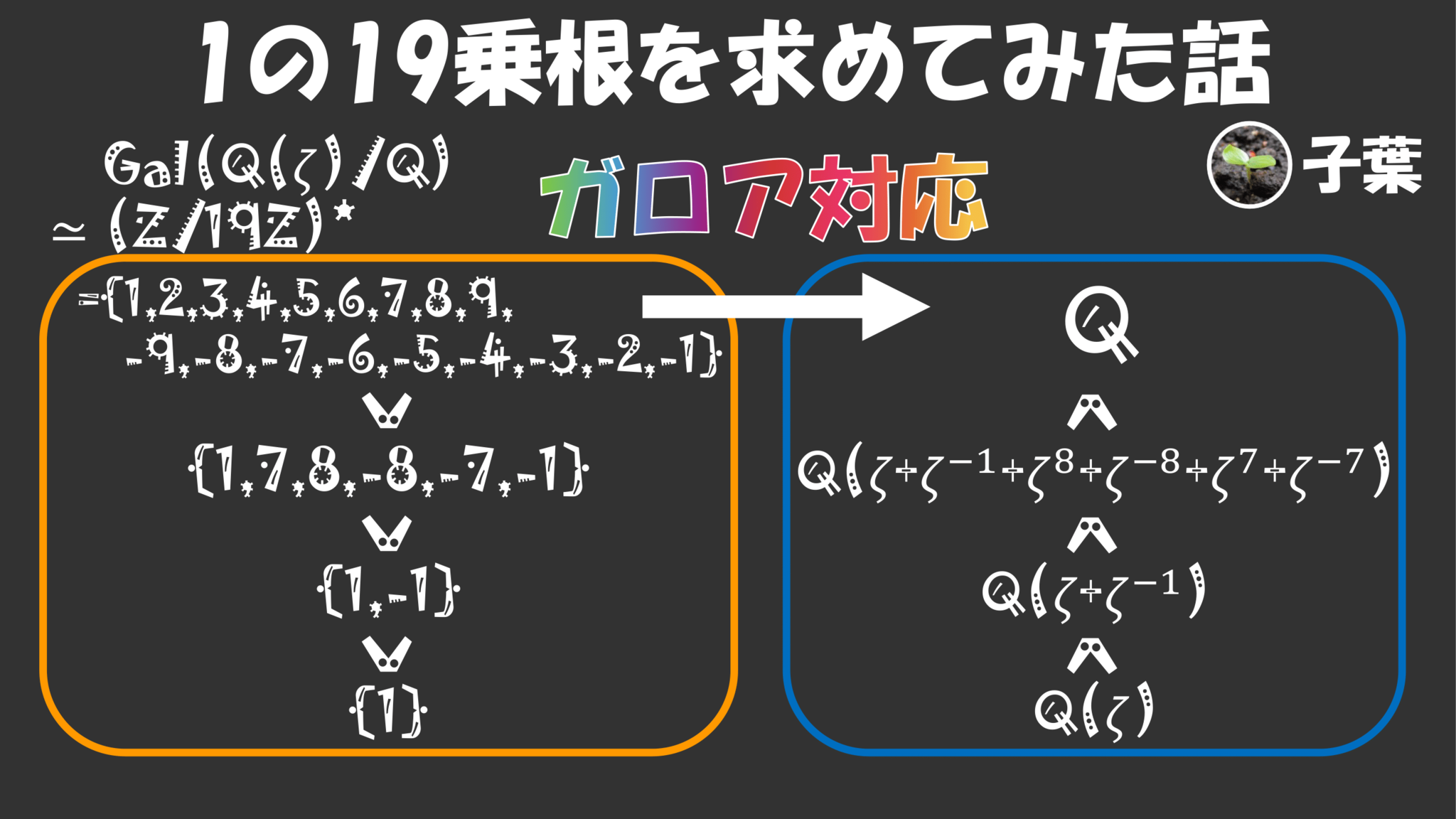
　というわけでテンションが上がりまして、じゃあ$17$の次の素数、$1$の$19$乗根を求めてみたい！と思ったわけですが、じゃあどうやって求めるのかと言うとガロア理論の「対称性が近い数ほど次数が近い」という定理を使うことになります。
　数学でよく出てくる「対称性」という言葉は「ある変換に対して不変であること」を言いますので、なんらかの「対称性の指標となる変換の集まり」があるわけなんですね。そしてガロア理論ではこの「変換の集まり」を「数の世界」に対応させることを考えます。
　さて、いま有理数$\Q$から$1$の$19$乗根$\Q(\z_{19})$を求めたいわけなのですが、その間の対称性には大きな差があり、直接求めようとするなら$18$次方程式とか$9$次方程式を解かなければいけなくなります。流石にそれは無理があるので$\Q$と$\Q(\z_{19})$間にいくつかの変換の集まりを挟んで、それに対応する世界を経由して順繰りに$\Q$から$\Q(\z_{19})$を目指していくことを考えます。

スライド9
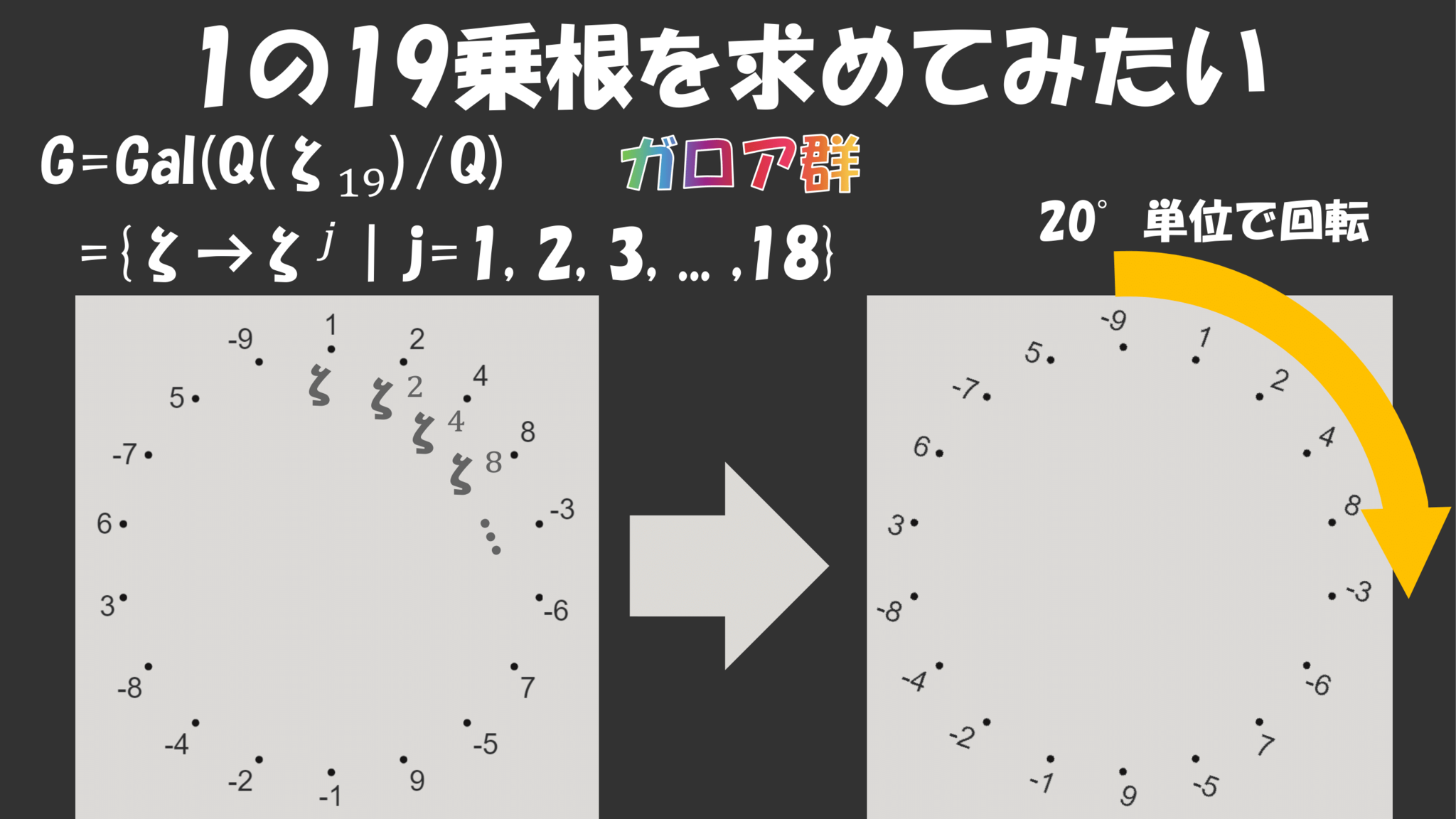
　そのためにはまず$\Q$のもつ対称性$G$とは何かということを知らなければなりません。この$G=\Gal(\Q(\z_{19})/\Q)$とはガロア群と言って、次のような変換と考えることができます。
　まず左図のように十八個の点にある規則($\mathrm{mod}\;19$における$2^k$の値)に従って数字が割り振られている図形があって、それぞれの点に$1$の$19$乗根$\z$の累乗が対応しています。この各点を$20^\circ$単位で回転させる変換、つまり$20^\circ,40^\circ,60^\circ,\ldots,360^\circ$回転の計$18$個の変換で$G$が構成されています。
　
スライド10
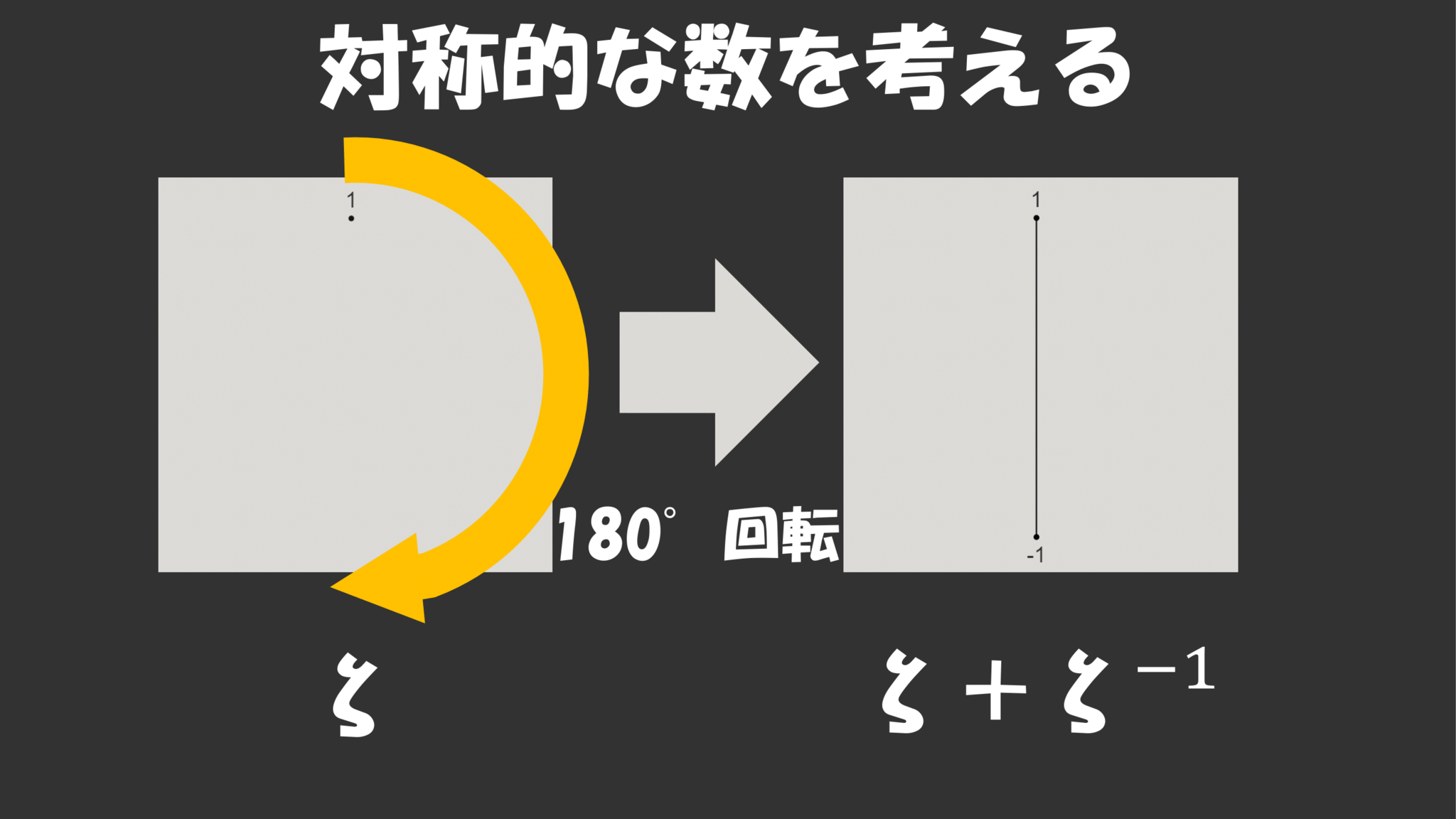
　というわけでこの変換に対して対称性というものを考えていきましょう。まずは一番対称性が低い状態、つまり一点だけの状態$\z$から対称性を増やしていくことを考えます。
　とりあえず$180^\circ$回転に対する対称性を考えると、点$1$とそれを$180^\circ$回転させた点$-1$を合わせると良さそうです。この"合わせる"というのは数の世界ではどうするのかというと、とりあえず単純に足し算することにしましょう。
　実際こうしてできた数$\z+\z^{-1}$は$180^\circ$回転させる変換、つまり$\z$を$\z^{-1}$に置き換える変換に対して
$\z+\z^{-1}\mapsto\z^{-1}+(\z^{-1})^{-1}=\z^{-1}+\z$
と不変になることがわかります。

スライド11
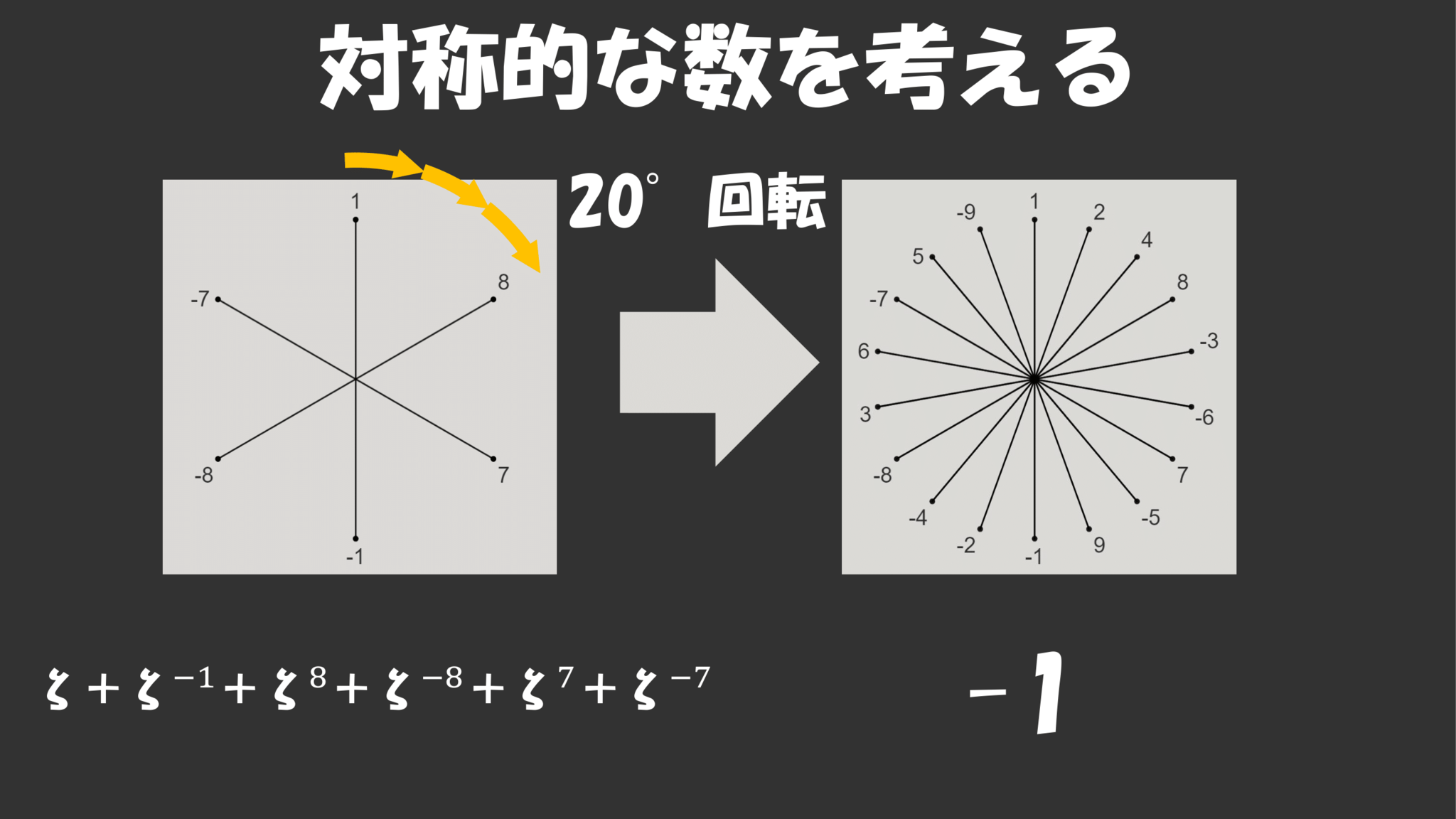
　次にこの図形$\z+\z^{-1}$に$60^\circ$回転に対する対称性を考えると右図のようになって、これもとりあえず足し合わせて$\z+\z^{-1}+\z^8+\z^{-8}+\z^7+\z^{-7}$という数を考えましょう。

スライド12
　そして最後に$20^\circ$回転に対する対称性を考えて足し合わせるとこれに対応する数は$-1$、つまり有理数となって、$\z$から有理数までの道が繋がりました。

スライド13
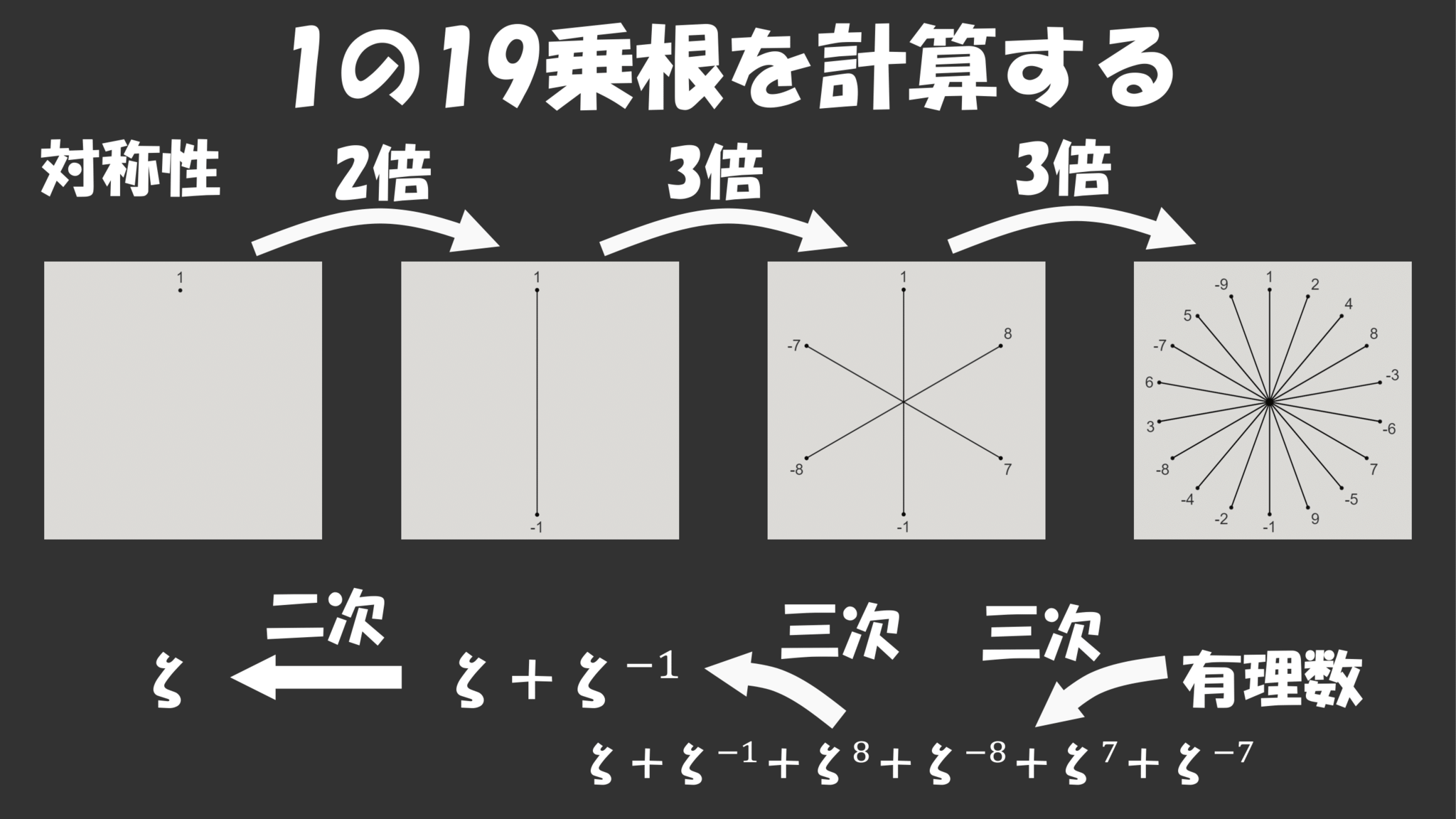
　こうしてこのような図形の列ができました。
　はじめに「対称性が近い数ほど次数が近い」と言いましたがさらに具体的に、この四つの図形が左から右に対称性が$2$倍、$3$倍、$3$倍と増えているのに対応して、有理数から$\z$に向かって三次、三次、二次方程式を経由することになります。
　この三つの方程式を解けば$1$の$19$乗根$\z$を求めることができるわけです。

$1$の$19$乗根を計算する

スライド14
　最後の二次方程式は
$\z=\cos\t+i\sin\t\quad(\t=2\pi/19)$
に対して
$\z+\z^{-1}=2\cos\t$
となっているので$\sin\t$と$\cos\t$の関係
$\sin\t=\sqrt{1-\cos^2\t}$
を使えば簡単に解決しますので、問題はこの二つの三次方程式になります。

スライド15
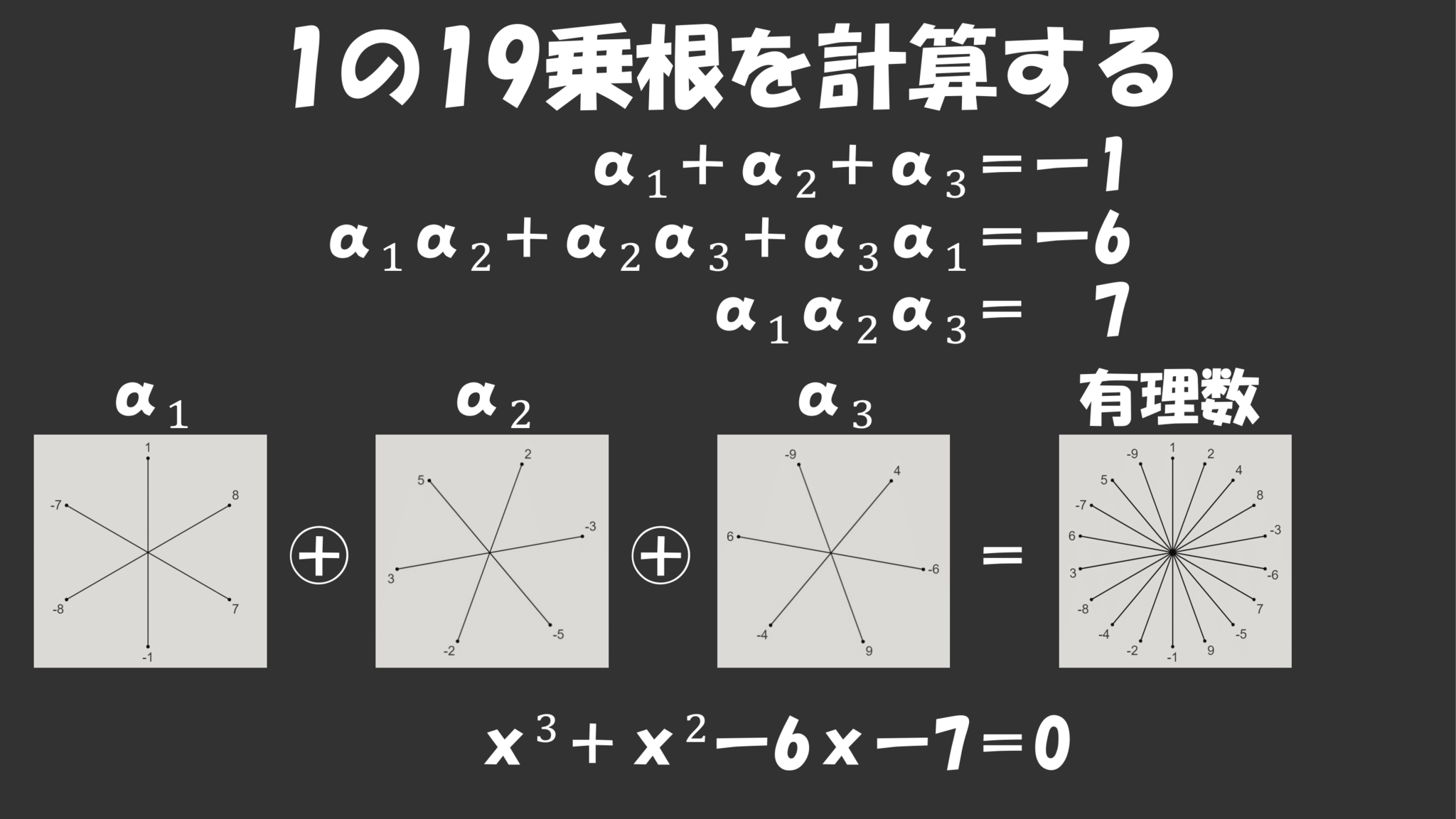
　まず有理数から$\a_1=\z+\z^{-1}+\z^8+\z^{-8}+\z^7+\z^{-7}$を求める三次方程式を考えましょう。
　先ほど図形$\a_1$から$20^\circ$回転に対する対称性を増やすことを考えたときに、$\a_1$を$20^\circ,40^\circ$回転させた図形$\a_2,\a_3$を足し合わせるということをしましたが、この"足し合わせる"というのは単純に数として足して
$\a_1+\a_2+\a_3$
とするだけではなく、掛けてから足して
$\a_1\a_2+\a_2\a_3+\a_3\a_1$
としたり、全部掛け合わせて
$\a_1\a_2\a_2$
としても対称性を増やすことができます。
　実際$20^\circ$回転させる変換は$\a_1$を$\a_2$に、$\a_2$を$\a_3$に、$\a_3$を$\a_1$に置換するので、これらの式はこの置換に対して不変となっていることがわかります。

スライド16 　
　$20^\circ$回転に対して対称的となる、つまり対称性が最大となるということは有理数になるということなので、これらの式を求めてみると実際次のように有理数となり、解と係数の関係から$\a_1,\a_2,\a_3$は方程式
$x^3+x^2-6x-7=0$
を満たすことがわかります。

スライド17
　次に$\a_1$から$\b_1=\z+\z^{-1}$を求める三次方程式を考えると、先ほどと同じように$\b_1$を$60^\circ,120^\circ$回転させた図形$\b_2,\b_3$に対し、
$\b_1+\b_2+\b_3$
だけでなく
$\b_1\b_2+\b_2\b_3+\b_3\b_1$
$\b_1\b_2\b_3$
も$\a_1$と同じ対称性を持つので$\a_1$の世界の言葉で書くことができ、その値を求めることで$\b_1,\b_2,\b_3$は方程式
$x^3-\a_1x^2+(\a_1^2-5)x+(\a_1^2-6)=0$
を満たすことがわかります。

スライド18
　というわけで問題の二つの三次方程式が求められましたし、これらを解くこと(ここが一番大変なのですが...)でこのように$1$の$19$乗根(の実部)を求めることができました！！！！！！！！！

スライド19

スライド20
　ということで、ご清聴ありがとうございました。

おまけ

　今回は僕が独自に求めた$n=19$の場合に絞って話をしましたが、$n$が別の素数のときや合成数であるときあどうなのか、という疑問もあると思うので簡単に答えておきます。
　一応$1$の冪根の値について簡単に求められる範囲で「 1の冪根をたくさん求めてみた(解説付き) 」という記事にリストアップしていますので良ければご覧ください。

$n$が複数の素因数を持つ合成数であるとき

　$n$が複数の素因数を持つ合成数であるときは$n=ml$($m,l$は互いに素)と分解できるので不定方程式
$mx+ly=1$
に整数解$x,y$があって、そのような$x,y$に対して$1$の$n$乗根$\z_n$は
$\z_n=\z_m^y\z_l^x$
と分解することができます。このように分解していくことで素数冪$p^e$に対して$\z_{p^e}$の表現が求まっていれば$\z_n$の表現もそこから求められることがわかります。

$n$が素数冪であるとき

　また$n$が素数冪$p^e$であるときはなんかズルい気がしますが、
$\z_{p^e}=\sqrt[p^{e-1}]{\z_p}$
と表現できるので素数$p$に対して$\z_p$の表現が求まっていれば$\z_{p^e}$の表現も求められます。実際$1$の$3$乗根
$\dis\z_3=\frac{-1+\sqrt3i}2$
に対して$1$の$9$乗根は
$\dis\z_9=\sqrt[3]{\frac{-1+\sqrt3i}2}$
以上の表現を(おそらく)持ちません。

$n$が素数であるとき

　そして$n$が素数$p$であるときは、今回の$p=19$のときとおおよそ同じように$\z_p$を求めることができますが、今回は
$p-1=18=2\times3\times3$
と素因数分解できたので二次方程式一回と三次方程式二回で$\z$が求められたのであって、$p-1$が$5$以上の素因数を持つ場合($p=23,29,31$など)は五次以上の方程式に直面することになります。もちろんよく知られている通り解の公式が存在しないため、別のアプローチが必要になるという点で今回と全く同じように$\z_p$が求められるというわけではありません。
　じゃあどうするのかということについては結構難しい話なので 私が前に書いた記事 とかを参照してください。「$1$の$n$乗根を含む体の$n$次巡回拡大は冪根拡大である」という定理の証明で具体的に冪根の形で表される原始元を構成しますが、そこら辺を理解しているとなんとなく意味は分かると思います。
　なんにせよ$p\geq23$ともなるといよいよ手計算は地獄になってくるので「求めてみよう！」とは思わない方がいいと思います。