4
レム・ツー・スリー・フォー ~レムニスケート上の点がつくる角度に関して~
211
0
$$$$
 勘が冴えていれば証明の方針も見えるはず
勘が冴えていれば証明の方針も見えるはず
はい構図ドーン、という体で、いきなり画像を掲載してみた。今回の記事では、レムニスケートにおいて成り立つ角度の関係(要するに上図)を見ていきたいと思う。いつも通り独自研究の成果であるが、初等幾何エンジョイ勢を自称する某氏から記事執筆中に先行研究(とは言っているが、件の研究と本記事の内容がどう関連しているのかを見抜ける人はほぼ皆無と思われるうえ、おそらく先行研究を記した人物でさえも本記事の内容に心当たりは無いであろう)を紹介されたので、暇な方は記事末尾の文献も読んでみよう。
構図(注:汎用性のある性質を幾何界隈ではこう呼びます)の紹介
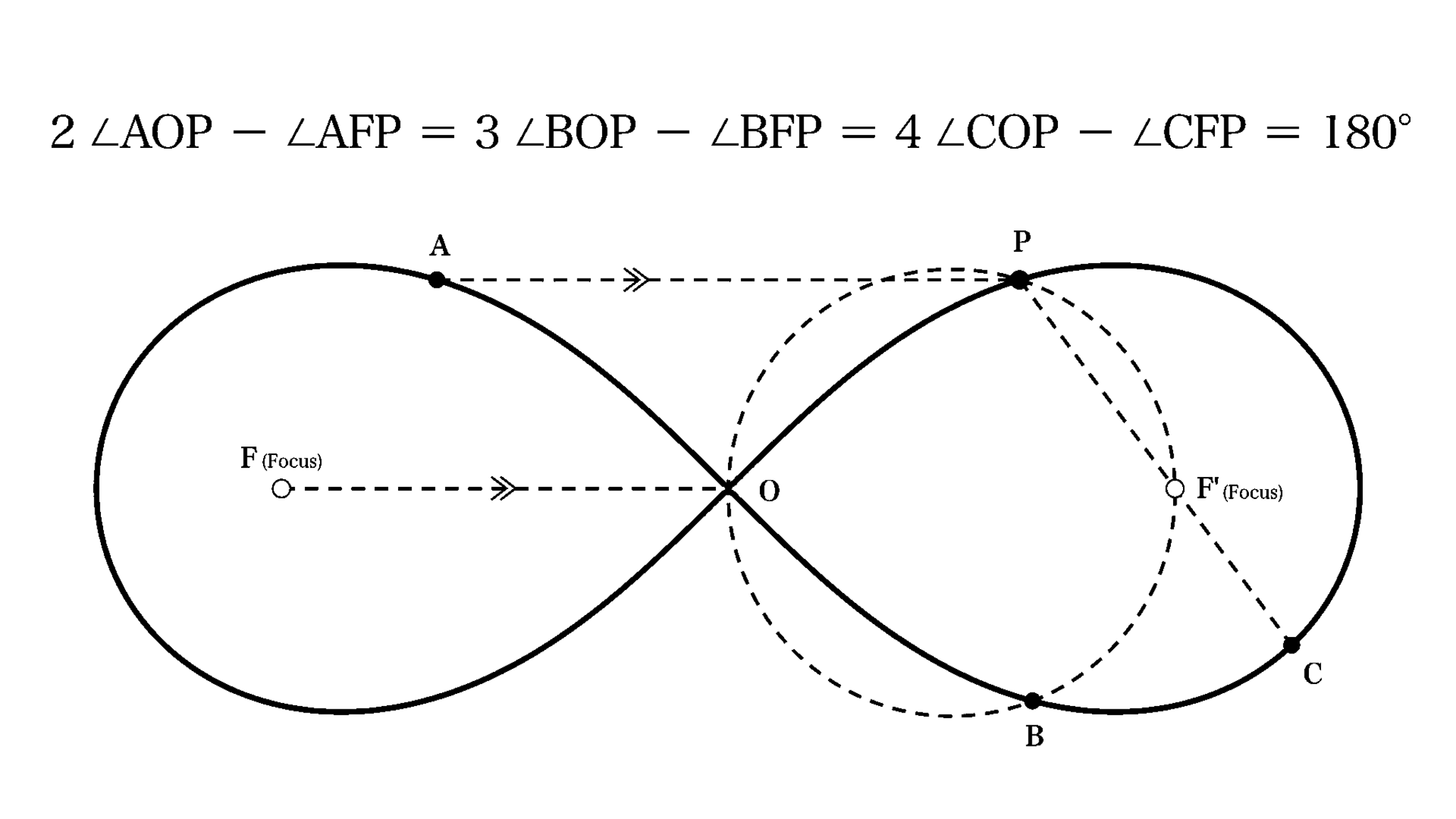
2点$F,F'$を焦点とするレムニスケート$\Lambda$の中心を$O$とし、$\Lambda$の周上に$\dfrac{OF}{\sqrt{5}}< PF'< OF$をみたす任意の点$P$をとる。線分$FF'$の垂直二等分線に関する$P$の対称点を$A$、$\triangle OF'P$の外接円と$\Lambda$の交点を$B$、半直線$PF'$と$\Lambda$の交点を$C$、と、それぞれ名付ける(ただし、いずれも$P$と異なる)。このとき、以下が成立する。
$$ 2\angle AOP-\angle AFP=3\angle BOP-\angle BFP=4\angle COP-\angle CFP={180}^{\circ}$$
$$ 2\angle AOP-\angle AFP=3\angle BOP-\angle BFP=4\angle COP-\angle CFP={180}^{\circ}$$
 不要かもしれませんが再掲します
不要かもしれませんが再掲します
$\dfrac{OF}{\sqrt{5}}< PF'< OF$の条件は図を成立させるために付けたもので、本質とは関係ない。各点が図2のような位置関係にあれば、自ずとみたされる条件である。
本質は、1番下の行に記した$2\angle AOP-\angle AFP=\dots$の部分。係数に$2,3,4$が1度ずつ登場しており、ビジュアルに特化した構図であることが伺える。構図はビジュアルが命、というのは、私の半世紀に亘る幾何研究で培われた確固たる信念であるすみません盛りました実際は2年くらいです。
本質は、1番下の行に記した$2\angle AOP-\angle AFP=\dots$の部分。係数に$2,3,4$が1度ずつ登場しており、ビジュアルに特化した構図であることが伺える。構図はビジュアルが命、というのは、私の半世紀に亘る幾何研究で培われた確固たる信念であるすみません盛りました実際は2年くらいです。
それでは、この構図を証明していこう。余談だが、一般的には$O$を二重点(Double point)と呼ぶらしい。本記事では分かりやすさのために、敢えて「中心」という表現を用いる。
構図の証明を丁寧に書きたい
一目見ただけで「証明は大変だな……」と直感を得た読者も多いだろう。実際、
前々回の記事
のように各点の座標を計算して、根性で加法定理を叩きつける証明方法も無くはない。しかし、あまりにも骨が折れる所業で、ともすれば日本国憲法第25条(2022年6月時点)に抵触しかねない。
よって、可能な限り楽をせんと試みる。以下をご覧あれ。
よって、可能な限り楽をせんと試みる。以下をご覧あれ。
【いちよんひくいちの補題】
2点$F,F'$を焦点とするレムニスケート$\Lambda$の中心を$O$とし、$\Lambda$の周上に$PF< OF$をみたす任意の点$P$をとる。ここで$\angle OFP=\alpha,$ $\angle FOP=\beta,$ $\angle OF'P=\gamma$とすると、$\alpha+4\beta-\gamma={180}^{\circ}$が成立する。
 実はこっちが本記事の核心だったりそうでもなかったり
実はこっちが本記事の核心だったりそうでもなかったり
$({\rm Lem.})$ 【いちよんひくいちの補題】の証明
2点$F,F'$の座標が$F(-1,0),F'(1,0)$となるように$xy$直交座標平面を設定すると、$\Lambda$の方程式は以下のように表される(有名事実)。
$$ \Lambda: \left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right)$$ いま、点$P$の座標を$P(a,b)$とすると、$P$は$\Lambda$上に存在するので、
$$ \left(a^{2}+b^{2}\right)^{2}=2\left(a^{2}-b^{2}\right)$$が従う。また、$\alpha$および$\gamma$について、$\tan\left(\alpha\right)=\dfrac{b}{a+1},$ $\tan\left(\gamma\right)=-\dfrac{b}{a-1}$は明らかである。
$$ \Lambda: \left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right)$$ いま、点$P$の座標を$P(a,b)$とすると、$P$は$\Lambda$上に存在するので、
$$ \left(a^{2}+b^{2}\right)^{2}=2\left(a^{2}-b^{2}\right)$$が従う。また、$\alpha$および$\gamma$について、$\tan\left(\alpha\right)=\dfrac{b}{a+1},$ $\tan\left(\gamma\right)=-\dfrac{b}{a-1}$は明らかである。
$\rm tan$の加法定理を用いると、
$$ \tan\left(\alpha-\gamma\right)=\dfrac{\dfrac{b}{a+1}-\left(-\dfrac{b}{a-1}\right)}{1+\dfrac{b}{a+1}\left(-\dfrac{b}{a-1}\right)}=\dfrac{2ab}{a^{2}-b^{2}-1}$$であるが、
$$ \left(2ab\right)^{2}+\left(a^{2}-b^{2}-1\right)^{2}=\left(a^{2}+b^{2}\right)^{2}-2\left(a^{2}-b^{2}\right)+1=1$$に注意することで、$\sin\left(\alpha-\gamma\right)=2ab,$ $\cos\left(\alpha-\gamma\right)=a^{2}-b^{2}-1$が判明する(正負も考慮した)。
ゆえに、$\rm tan$の半角公式(の変形版)を適用して、$\tan\left(\dfrac{\alpha-\gamma}{2}\right)$は以下のように求められる。
$$ \tan\left(\dfrac{\alpha-\gamma}{2}\right)=\dfrac{\sin\left(\alpha-\gamma\right)}{1+\cos\left(\alpha-\gamma\right)}=\dfrac{2ab}{a^{2}-b^{2}}$$
$$ \tan\left(\alpha-\gamma\right)=\dfrac{\dfrac{b}{a+1}-\left(-\dfrac{b}{a-1}\right)}{1+\dfrac{b}{a+1}\left(-\dfrac{b}{a-1}\right)}=\dfrac{2ab}{a^{2}-b^{2}-1}$$であるが、
$$ \left(2ab\right)^{2}+\left(a^{2}-b^{2}-1\right)^{2}=\left(a^{2}+b^{2}\right)^{2}-2\left(a^{2}-b^{2}\right)+1=1$$に注意することで、$\sin\left(\alpha-\gamma\right)=2ab,$ $\cos\left(\alpha-\gamma\right)=a^{2}-b^{2}-1$が判明する(正負も考慮した)。
ゆえに、$\rm tan$の半角公式(の変形版)を適用して、$\tan\left(\dfrac{\alpha-\gamma}{2}\right)$は以下のように求められる。
$$ \tan\left(\dfrac{\alpha-\gamma}{2}\right)=\dfrac{\sin\left(\alpha-\gamma\right)}{1+\cos\left(\alpha-\gamma\right)}=\dfrac{2ab}{a^{2}-b^{2}}$$
ところで、$\beta$について$\tan\left(\beta\right)=-\dfrac{b}{a}$がいえるので、$\tan\left(2\beta\right)$を求めると、
$$ \tan\left(2\beta\right)=\dfrac{2\cdot\left(-\dfrac{b}{a}\right)}{1-\left(-\dfrac{b}{a}\right)^{2}}=-\dfrac{2ab}{a^{2}-b^{2}}$$となる。すなわち$\tan\left(\dfrac{\alpha-\gamma}{2}\right)=-\tan\left(2\beta\right)$であり、$0^{\circ}<\alpha-\gamma<{180}^{\circ},$ $0^{\circ}<\beta<{45}^{\circ}$に注意すると$\alpha+4\beta-\gamma={180}^{\circ}$を得る。 ($({\rm Lem.})$の証明終)
$$ \tan\left(2\beta\right)=\dfrac{2\cdot\left(-\dfrac{b}{a}\right)}{1-\left(-\dfrac{b}{a}\right)^{2}}=-\dfrac{2ab}{a^{2}-b^{2}}$$となる。すなわち$\tan\left(\dfrac{\alpha-\gamma}{2}\right)=-\tan\left(2\beta\right)$であり、$0^{\circ}<\alpha-\gamma<{180}^{\circ},$ $0^{\circ}<\beta<{45}^{\circ}$に注意すると$\alpha+4\beta-\gamma={180}^{\circ}$を得る。 ($({\rm Lem.})$の証明終)
はい補題ドーン。これをやりたくて冒頭で構図をドーンした。驚いてくれただろうか
。万一読者の中で心臓に基礎疾患をお持ちの方がいれば少々申し訳ないが。
話を戻す。こちらの【いちよんひくいちの補題】、実は最初の構図の証明に使える優れもの。本補題と最初の構図との関係を確認しよう。
 再々掲は流石に過剰かもしれない
再々掲は流石に過剰かもしれない
$(2)$ $2\angle AOP-\angle AFP={180}^{\circ}$について
$$\begin{eqnarray} \angle AOP&=&{180}^{\circ}-\angle FOA-\angle F'OP={180}^{\circ}-2\angle FOA \\[6pt]
\angle AFP&=&\angle OFA-\angle OFP=\angle OFA-\angle OF'A
\end{eqnarray}$$であるから、【いちよんひくいちの補題】より、
$$\begin{eqnarray} 2\angle AOP-\angle AFP&=&{360}^{\circ}-\left(\angle OFA+4\angle FOA-\angle OF'A\right) \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(2)$の証明終)
$$\begin{eqnarray} 2\angle AOP-\angle AFP&=&{360}^{\circ}-\left(\angle OFA+4\angle FOA-\angle OF'A\right) \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(2)$の証明終)
$(3)$ $3\angle BOP-\angle BFP={180}^{\circ}$について
【いちよんひくいちの補題】より、
$$\begin{eqnarray} \angle OF'P+4\angle F'OP-\angle OFP&=&{180}^{\circ} \\[6pt] \angle OF'B+4\angle F'OB-\angle OFB&=&{180}^{\circ} \end{eqnarray}$$を得て、これらを辺々足し合わせると、
$$ \angle BF'P+4\angle BOP-\angle BFP={360}^{\circ}$$となる。四角形$OBF'P$が円に内接することから$\angle BF'P+\angle BOP={180}^{\circ}$が従うので、
$$\begin{eqnarray} 3\angle BOP-\angle BFP&=&\left(\angle BF'P+4\angle BOP-\angle BFP\right)-\left(\angle BF'P+\angle BOP\right) \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(3)$の証明終)
$$\begin{eqnarray} \angle OF'P+4\angle F'OP-\angle OFP&=&{180}^{\circ} \\[6pt] \angle OF'B+4\angle F'OB-\angle OFB&=&{180}^{\circ} \end{eqnarray}$$を得て、これらを辺々足し合わせると、
$$ \angle BF'P+4\angle BOP-\angle BFP={360}^{\circ}$$となる。四角形$OBF'P$が円に内接することから$\angle BF'P+\angle BOP={180}^{\circ}$が従うので、
$$\begin{eqnarray} 3\angle BOP-\angle BFP&=&\left(\angle BF'P+4\angle BOP-\angle BFP\right)-\left(\angle BF'P+\angle BOP\right) \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(3)$の証明終)
$(4)$ $4\angle COP-\angle CFP={180}^{\circ}$について
【いちよんひくいちの補題】より、
$$\begin{eqnarray} \angle OF'P+4\angle F'OP-\angle OFP&=&{180}^{\circ} \\[6pt] \angle OF'C+4\angle F'OC-\angle OFC&=&{180}^{\circ} \end{eqnarray}$$を得て、これらを辺々足し合わせると、
$$ \angle CF'P+4\angle COP-\angle CFP={360}^{\circ}$$となる。$\angle CF'P={180}^{\circ}$に注意すると、
$$\begin{eqnarray} 4\angle COP-\angle CFP&=&\left(\angle CF'P+4\angle COP-\angle CFP\right)-\angle CF'P \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(4)$の証明終)
$$\begin{eqnarray} \angle OF'P+4\angle F'OP-\angle OFP&=&{180}^{\circ} \\[6pt] \angle OF'C+4\angle F'OC-\angle OFC&=&{180}^{\circ} \end{eqnarray}$$を得て、これらを辺々足し合わせると、
$$ \angle CF'P+4\angle COP-\angle CFP={360}^{\circ}$$となる。$\angle CF'P={180}^{\circ}$に注意すると、
$$\begin{eqnarray} 4\angle COP-\angle CFP&=&\left(\angle CF'P+4\angle COP-\angle CFP\right)-\angle CF'P \\[6pt] &=&{360}^{\circ}-{180}^{\circ}={180}^{\circ} \end{eqnarray}$$がいえる。 ($(4)$の証明終)
……と、以上のように、【いちよんひくいちの補題】ただひとつを証明するだけで、他の構図がすべて得られる。要するに、最初の構図は補題の系でしかないのだ。(構図の証明終)
あとがきに示唆を込めて
以上、補題が頑張るだけの構図であった。最初の構図紹介で囲み枠が青色になっていることから「あ、この構図は何かの定理から自明に導かれるのだな」と予感した読者がいれば、私の記事をよく読んでくれているという意味になろう(問題は橙色、定理は緑色、系は青色、という風に囲み枠の色を使い分けている)。
最後に。【いちよんひくいちの補題】について、先述の先行研究にそれを導出するための幾何学的性質が隠されている。つまり、補題がそのまま書かれているわけでもなければ、補題と類似の構図があるわけでもない。折角なので、読者のために追体験の機会を残しておく。要するに、宝探しの感覚で文献を読んでみよう、補題への手がかりを探し出そう、ということだ。
他の先行研究や、本記事の誤謬などを見つけた方は、いつものようにコメントをお願いしたい。
他の先行研究や、本記事の誤謬などを見つけた方は、いつものようにコメントをお願いしたい。
遠くから「補題だけ書けばよいのでは?」という声が聞こえてきたけれども、初めに書いた通り、「構図はビジュアルが命」。補題よりもビジュアルで優れた(と思われる)系を見つければ、そちらを主軸に据えたほうが記事の充実度も高まるだろう。
参考文献
投稿日:2022年7月3日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中
