数学オリンピック体験記2022-2 春合宿～IMOまで
前回の記事 は読んでいただけたでしょうか? 今回は春合宿の感想戦からです! 張り切っていきましょう!
分野について
- A $\cdots$ 代数. 本選以降はさらにFE(関数方程式), 不等式に分けられる(まれにその他もある)
- C $\cdots$ 組み合わせ
- G $\cdots$ 幾何
- N $\cdots$ 整数論
コンテストの略称
- JMO $\cdots$ 日本数学オリンピック
- JJMO $\cdots$ 日本ジュニア数学オリンピック
- IMO $\cdots$ 国際数学オリンピック
- APMO $\cdots$ アジア太平洋数学オリンピック
- 春合宿 $\cdots$ 3月下旬の代表選考合宿
- 初夏合宿 $\cdots$ 5月上旬の代表強化合宿
本の略称
- パフェマス $\cdots$ ○○パーフェクトマスター/日本評論社
- 獲得 $\cdots$ 獲得金メダル！ 国際数学オリンピック メダリストが教える解き方と技/朝倉書店
- EGMO $\cdots$ Euclidean Geometry in Mathematical Olympiads/MAA Problem Book Series
内容はあくまで一個人の意見として軽く受け止めてください！
春合宿
春合宿のコンテスト問題のネタバレを含みます!!
いよいよ春合宿. JJMOで一度行ったときはちょうどコロナが出始めた年で, コンテストも2日間だけでしたので, かなり新鮮な気持ちでした. また, APMOのときに会えなかった西日本勢は初の顔合わせです. 緊張します. その一方でもちろん, 楽しみでもありました.
試験は3問4時間半(7点/問)$\times$4日間, 1番級から3番級まで各分野が1回ずつ出題されます. また, 答案や点数は初夏合宿で(代表だけ)分かります.
Day1
- $n\ge3$を整数とする. $m\ge n+1$個の宝石からなるネックレスについて, 各宝石を$n$色で塗ることを考える. このとき, 「どの連続する$n+1$個の宝石についてもそれらの彩色に$n$色使われている」という状態を実現できない最小の$m$を求めよ.
- $f:\mathbb{R}\rightarrow\mathbb{R}$, $f(xf(y)+f(f(y)))+yf(f(x))=f(f(y)f(f(x))+f(y))+xy$
- $a_1,a_2,a_3,\ldots$を任意の正の整数$n$, $m$について$a_{n+2m}$が$a_{n}+a_{n+m}$を割り切るような正の整数からなる数列とする. このとき, 数列は十分先で周期的になる, すなわち, ある正の整数$N$, $d$が存在して$n>N$なる任意の正の整数$n$に対して$a_n=a_{n+d}$が成立することを示せ.
実は春合宿が始まるまで, 代表になるつもりがそこまでなく(そもそも2番級以降が安定して解ける自信が全くなかった), 春合宿の目標もとにかく楽しむこと!たくさん交流すること!でした. ですので, 初日もかなりリラックスした状態でコンテストに臨むことができました. 席が右が新井さん, 後ろが北山さんと話せる人が多かったこともあったと思います.
分野を見るとCAN. 1問かあわよくば2問くらいの気持ちで解き始めます. 1は実験をし, 違和感を言語化していくと鳩ノ巣が綺麗に見えてきました. 構成も評価のときの発想から着想を得ることができたため特に難航することはなく, 1時間かからないくらいで解答を書き終えられました.
問2. A分野には一番苦手意識があったため, 解けたらいいな, くらいで解き始めます. 自明な考察をいくつかしていき, $f(0)$の値で場合分けをすることに気づきます. $f(0)=0$の場合はすぐわかり, そうでない場合が難しいですね.
$f(f(x))=x+c$という式を得た後, ほかの式変形に行く前に"直感的に", この式からまだ何か得られる情報がある, と察知しました. この直感は実際あたっていて(!), $f(x)+c=f(f(f(x)))=f(x+c)$という変形ができたのです. これに限った話ではなく, 試験中直感が働いたら一旦それを信じてみてください. 経験上かなりの確率で当たります. この式変形は案の定かなり本質的で, ここから多少の右往左往はあったものの2時間と少しで解き終わりました.
問3にうつりますが, 初手で大きく方針を間違えてしまい, これといった進捗が出ないまま試験終了.
結果は770でした. 苦手分野で解けたらいいくらいの心構えでもやはり解けないと焦ります. そういったとき, 自分の自信につながることを思い出すのがおすすめです. 春合宿では自分が最近褒められた経験を思い出したりしました. あらかじめ思い出すことを決めておくと冷静になれます.
Day2
各整数$n\ge 1$に対して$\displaystyle\sum_{k=1}^{n}\left\lfloor\frac{a_k}{k}\right\rfloor$の最小値を求めよ. ただし, $(a_1,\dots,a_n)$は$(1,\dots,n)$の並べ替えである.
$r>1$を有理数とする. 太郎は数直線上でゲームを行う. はじめ, 赤いビーズが$0$に配置され, 青いビーズが$1$に配置される. $1$回の動きで, 太郎は一つのビーズとある$k \in \mathbb{Z}$を選ぶ. 選ばれたビーズが数直線上の$x$にあり, もう一方が$y$にあるとき, $x$にあるビーズは$x'-y=r^k(x-y)$をみたすような$x'$にうつされる.
太郎が赤いビーズを$2021$回以内に$1$に移せるような$r$を全て求めよ.線分$MN$を直径とする円$ω$の内部に$A$がある. $N$を中心とし, 線分$NA$を半径に持つ円と$ω$の交点を$B, C$とする. 線分$BC$上に$\angle BAP=\angle CAQ$なる$P, Q$を取り, 直線$NP, NQ$と$ω$の交点をそれぞれ$X,Y$とおくとき, $3$直線$XQ, YP, MA$が一点で交わることを示せ.
Day1が終わった後話した人はほぼ全員2完. このときは代表になることへの希望よりも苦手分野の2番級が解けた嬉しさが勝っていました.
分野がAC(?)G. 1も2もあまり見慣れないタイプの問題だったため, 難易度の想像がつきません. 1は実験していくと評価が$n\rightarrow n/2\rightarrow \log_2n$と改善されていき, $\log_2n$の構成ができた時点で答えを確信しました. 証明も記述量は多かったものの実験でやったことがかなり直感的に帰納法で回り, ($2$べき$-1$の場合)それ以外も$2$べきの構成からうまく示せました. これも1時間ちょっとで.
2ははじめ(というか試験終了までずっと)Cだと思っていたのですが, 終わったあとほかの参加者からNだと指摘され少し残念な気持ちに. この問題は問題の定式化が本質部分でした. しかも前半で触れた, 解答用紙にいきなり解答を書き始める, という手段を取ったらなんとそのままとんとん拍子に解けてしまった. 実際は初夏合宿で帰ってきた答案を見ると説明の曖昧さで2点引かれていたのでなんとも言えませんが... 数式をたくさん使うように, というアドバイスをいただきました. 1と合わせて2時間半くらい. そして3...
永遠に方針が見えません. いろいろ実験はしてみるもののこれといった情報が何も手に入らない. 複素で解こうとしてもいまいち刺さらない. 結局なにもできないまま試験終了.
結果は750でした. この日もあまり差はつかず, 特に話した高2(04世代)は全員4完以上していました. 後半二日で何か起こる予感がしました.
Day3
$ABCD$を$AC=BC$なる平行四辺形とする. 半直線$AB$上に点$P$をとったところ, 三角形$ACD$の外接円が線分$PD$と$D$でない点$Q$で交わった. 三角形$APQ$ の外接円が線分$PC$と$P$でない点$R$で交わるとき, $3$直線$CD,AQ,BR$が一点で交わることを示せ.
忘れました...(C分野, グラフの問題, 感想は雰囲気でお楽しみください)
$f:\mathbb{R}→\mathbb{R}$, $f(x)f(y)-f(x+y)=yf(x)-f(x+f(y))$かつ$f(-1)=-1$
分野がGCAで, まず確実に1番は解こうという気持ちに. 共点の示し方を根心くらいしか知らなかったので()とりあえず根心を考えると, 一瞬で解けてしまいました. 解答を書く時間を含めても30分くらい. これはかなりの想定外でした. また, この問題では北山さんが普段幾何を解くスタイルの「円を一切書かない」というのを実践してみました. それが功を奏したのかもしれません(?)
3Aは絶対解ける自信がないので2Cに全振り. ただ, 問題文が異様に長い. 某試験を彷彿とさせるような異様な長さ. 読解から始めていくと後半3行がグラフの用語で「強連結」一語で記述できることに気づきます. C分野はグラフ用語に直すと本質が見えやすくなることが多いです. グラフの考察を進めるもうーん. 全然わかりません. 必要性のほうはなんとなく示せた感じがしましたが十分性がよくわからない. 最後10分くらいでそれっぽい解法を見つけ全速力で書き進めますが, 結局必要性も十分性も間違っていたらしく1点どまり(おそらく大量の記述のどこかが刺さった).
ちなみに2Cを解いている途中, 隣の新井さんから30分から1時間に1回くらい大きなため息が聞こえてきて, そのたびに進捗を生んでいると思い,「やっぱりみんな2完しているよな...」と焦りと諦めの気持ちが募っていました.
3Aは少しも触りませんでした.
結果は710, かなり渋い. ただ, 全員1完($+\alpha$くらい)で安心する気持ちと, 最終日にすべてが決まる不安とが入り混じっていました. 終わったあと新井さんに何完か聞かれ1完ちょいと答えた瞬間抱きついてきたのが忘れられないです()(
その日新井さんがなにを経験していたか
).
ここまで来たら最終日2完以上して代表になってやろうという気持ちが芽生えます.
Day4
以下の条件を満たす正の整数$n$を全て求めよ:
- $n$のすべての正の約数のある並べ替え$(d_1, d_2,\dots,d_k)$が存在し, 任意の$i=1, 2, \dots,k$に対し$d_1+d_2+\dots+d_k$が平方数になる.
円$\Omega$に内接する四角形$ABCD$について, 点$D$の$\Omega$での接線が半直線$BA$, $BC$とそれぞれ$E$, $F$で交わっている. 三角形$ABC$の内部の点$T$ が$TE\parallel CD$, $TF\parallel AD$を満たしており, $D$と異なる線分$DF$上の点$K$が$TD=TK$を満たすとき, $3$直線$AC,DT,BK$が一点で交わることを示せ.
ハンターと透明なウサギが無限に広がるマス目でゲームをしている. はじめハンターは有限色で各マス目を彩色し, ウサギは最初にいるマスを一つこっそり選ぶ. その後$1$分に$1$回, 現在いるマスの色をハンターに伝えたのち, 今までに訪れたことがなく, かつ今いるマスと辺を共有しているマスにこっそり移動する. 有限の時間で以下のいずれかが成立すればハンターの勝利である:
- ウサギが動けなくなる
- ハンターがウサギの最初にいたマスを特定できる
このとき, ハンターには必勝法が存在するか.
コンテストも4日目, 大詰めです. かなり疲労がたまっていました. 分野はNGCと分かっていたため, 意地でも2完すると決めていました. 1は実験すると$1, 3, 5, 7,\dots$という構成が見つかり, 項数は無限ですがこれをうまく除くのが本質だと考えます. 結局項の中の大きめの素数$p, q$をとってくると$pq$があらわれてそこまでが全部公差$2$で埋まるという(あまりきれいではない)方針で解きました(ここの詰めが甘くて1点減点された). 1時間半くらいで解答を書き終えました.
そして2... 緊張が極限まで高まっています. $T$と$AC$を軸に対称な点を取ることに気づき, うまく共円や相似が見つかります. 示すべきことも平行になり, かなり示しやすくなりました(共円+平行でaminoの補題だと思ったそこのあなた, 当時僕はaminoの補題を知りませんでした). ただ, そこから30分くらい何も進捗が生まれないです.
このときあることに気づきます. 「この配置, 長さ計算で全部求まる」, と. 決心しました. 必ず解ききってやる. 時短もかねて解答用紙に計算を始めていきます. 計算量を見積もっても試験中におわるかどうか微妙な量でした. 途中3回ほど計算ミスがあり, 泣きそうになります. ただ, もう後戻りできないところまで来てしまっている. 死ぬ気で計算を続け, ついに残り10分. 計算をし終わります. 計算した解答用紙5枚. 最後10分は過呼吸が止まらずただ呆然としていました.
結果は670. 周りには(昨日までに5完だった人の中でも)0完から3完までいました. かつてないほどの満足感. ところが, 終わったあと色々な人に話を聞くとどうやら7完以上が6人いるらしいーーその6人がまさしく新井, 井本, 北村, 北山, 沖, 三宮だったのでした. その6人がのちに代表になるというのはまだ先のお話ですので, その日は必死に神頼みをしていました.
春合宿～IMO
終わった後, かつてないほどの燃えつきを味わっていました. 代表になるかどうかは, なれる確率もなれない確率も$10\%$くらいの印象. なっても奇跡, なれなくても何かの間違い. 悶々とした日々が2週間ほど過ぎそして...
4月の上旬, 春休みも折り返しを過ぎたころ代表になったという旨のメールが届きます. メンバーは例の6人. 最初の段階で全く代表になれる気がしていなかった分嬉しさと不安, そしてやる気が極限状態に達していました.
ーー自分には何が足りないか. "安定感"でした. 2番級を安定して解ける実力. それがとてもあったとは言えません. その弱点を克服するためにIMOまでは
- shortlistをやりこむ
- 幾何をとにかく重点的にやる
の二つをメインで取り組みました. 要望がありましたのでshortlistの解説をします.
shortlistとは
IMOの問題はコンテスト直前の会議でIMO shortlistと呼ばれる問題群から選ばれる. 問題は各国から送られてくる. shortlistは毎年作られ, 問題が使用されたIMOから1年間はオフィシャルには公開されない. その間は各国の代表選抜試験で使用されたり, 代表強化に使うことができる(そのため春合宿や初夏合宿の問題は口外してはいけない). 1年たてばAoPSや公式サイトで公開されるため自由に演習問題として使用することができる.
内容は
- 4分野(A, C, G, N)$\times$7～9問程度
が毎年あり, 各分野1～3$\cdots$1番級, 3～5$\cdots$2番級, 5～$\cdots$3番級くらいの印象. AoPSのフォーラム(問題横の"view topic")から大体解答は見られる. 実際のコンテスト問題の次にIMOに近い問題.
また, 幾何はEGMOをメインで取り組みました. Evan Chenによる幾何の対策書で, 英語で書かれています.
EGMO(分野別(幾何)/本選～/一部解説, 全問題ヒントあり)
Euclidean Geometry in Mathematical Olympiads. 洋書. JMO入賞の副賞としてもらい, 幾何はこれを中心に取り組んだ.
メリット
- 内容や問題量がとにかく充実している. 円周上の調和点列などはこの本で初めて知った
- 複素, 重心座標, 直交座標, 長さ計算, 三角関数全部対応している
- 英語とは言えどかなり読みやすい
- インターネット上に誤植集が上がっている
デメリット
- ほとんどない気がするが, 強いて言えば英語ということで若干ハードルが高いかもしれない(そんなに高くないです!!)
- 届くまでに場合によっては時間がかなりかかる
幾何に少しでも苦手意識がある人は一度誰かに見せてもらうのがおすすめです.
この間5月に強化合宿があったのですが, これの内容は秘密にしておきます. おおまかには本番形式の演習, 春合宿の解説, ほかの代表やチューターとの交流などです.
このほかに計4回の通信添削がありました. 1回6問(本番形式)を解いて財団に送り, 添削していただけるという制度です. 問題はMath Olympianに載ります.
また, shortlistは最終的にこのような感じになりました.
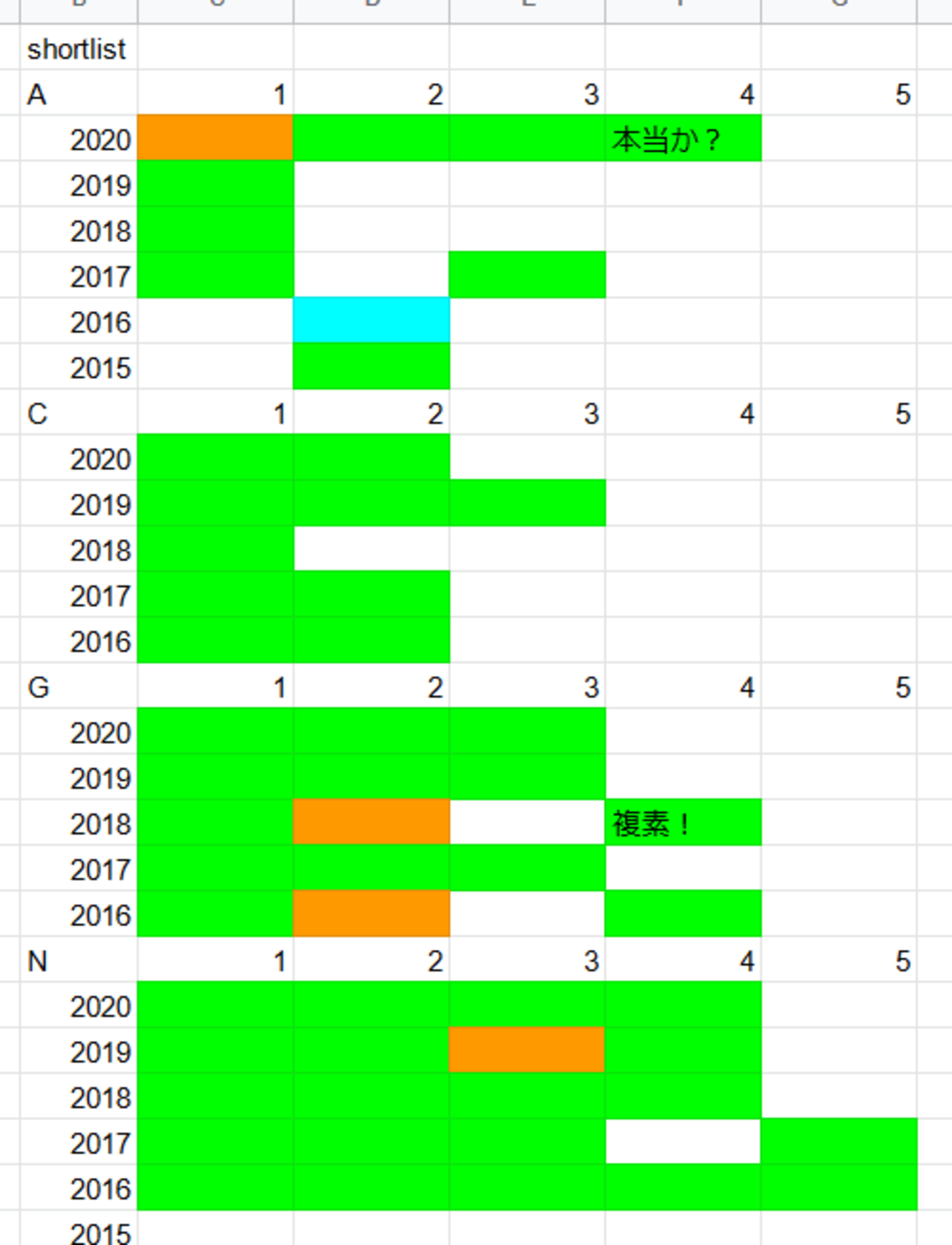shortlistの進捗状況
Aが壊滅的にできません. 特に不等式. もう少し全体的に取り組めばよかったと少し後悔しています. あとは3番級をしっかり解くだけ解いてみるなどしたほうがよかったと思っています. 一回も解いたことがない($\Rightarrow$解けたことがない)と本番で解くというモチベーションが下がってしまいます.
こんな感じで色々あり, 最終的には添削問題の手ごたえからしても, 当初の目標であった2番級を安定して解くというのは(Aを除けば)ほとんど達成されていた気がします. IMOの実感は最後までほとんどありませんでした.
IMO
何ていうか本当に実感がない. これからノルウェーに行くという実感もコンテストを受けるという実感も本当に何もわかない. どうやらあまりに非日常なことが重なると人は実感がなくなるらしいです.
"Math"logなのでコンテストをメインに書きます(). ほかの内容は財団が発行する通信に載ると思いますので是非そちらも読んでみてください!(宣伝)
コンテストまで
行きの飛行機ではELMOというコンテストの問題や精選Cをやっていました.
精選シリーズ(分野別/予選～/解答解説)
組み合わせ論, 三角法, 数論があり, それぞれ102, 103, 104問載っている. うち半分が初級, 半分が上級. 上級とは言っても2番級くらいまでの印象. 行きの飛行機で読んだだけなので簡単に.
メリット
- Cを読んだが好みの問題が多かった(人によるが)
- 日本語の分野別対策本がそんなにないのでそれだけでメリット
デメリット
- 問題と解答解説だけ(デメリットではないが)
純粋に問題が欲しい人はかなりおすすめできます.
現地についてからはあまり問題を解くことはできず, 前半で触れたまとめノートを見返したり, 同室の新井さん, 井本さんと幾何を数問解いたりしました.
コンテスト
Day 1
- オスロ銀行ではアルミ製の硬貨($A$表す)とブロンズ製の硬貨($B$で表す)の$2$種類の硬貨を発行している. 慶子さんは$n$枚のアルミ製の硬貨と$n$枚のブロンズ製の硬貨を持っており, これらの$2n$枚の硬貨は$1$列に並べられている. $1$種類の硬貨からなる連続する部分列を「鎖」とよぶことにする. ある$2n$以下の正の整数$k$に対して, 慶子さんは以下の操作を繰り返し行う.
左から$k$枚目のコインを含む最も長い鎖をとり, その鎖に含まれるコインをすべて
列の一番左に移す. たとえば$n=4, k=4$のとき, 最初のコインの並べ方が$AABBBABA$であるとすると, 操作の
過程は次のようになる.
$$AABBBABA\rightarrow BBBAAABA\rightarrow AAABBBBA\rightarrow BBBBAAAA\rightarrow BBBBAAAA\rightarrow\cdots .$$
$1\le k\le 2n$なる組$(n, k)$であって, どのような最初のコインの並べ方についても, 操作を何回か行った後に, 列の左から$n$枚のコインの種類がすべて等しくなるようなものをすべて求めよ. - $\mathbb{R}^+$を正の実数全体からなる集合とする. 関数$f : \mathbb{R}^+ \rightarrow\mathbb{R}^+$であって, 任意の$x\in\mathbb{R}^+$
に対して, $xf(y)+yf(x)\le2$なる$y\in\mathbb{R}^+$がちょうど$1$つ存在するようなものをすべて求めよ. - $k$を正の整数とし, $S$を奇素数からなる有限集合とする. このとき, 次の条件をみたす
ように$S$の要素を$1$つずつ円周上に並べる方法は高々$1$通りしかないことを示せ. ただし, 回転や裏返しで一致する並べ方は同じものとみなす.- 隣接するどの$2$つの要素の積も, ある正の整数$x$を用いて$x^2+x+k$と表される.
CAN. 1で沼らないといいなーと思いながら解き始めます. 実験をしていくとかなり自明な気がしてきます. 自明だと思ったらその言語化. 今回は「混ざっているのが少しずつ戻っていく」を数学の言葉にしてあげればよいですね. 具体的には$A$と$B$の間が何か所あるか, みたいな感じで行けました. 端の部分の評価が少し不安でしたが30分くらいで解答を書き終わります.
問2. 問題文が短いのでできることが少なそうです. 解はどう見ても$\frac1x$なので$g(x)=xf(x)$とおくために変形をします(JMO2007-2みたいな意識). $y$がちょうど一つという条件がおそらくかなり強い条件なので$y=\varphi(x)$みたいにします. すると, $xf(x)\le1$がすぐに言え, 逆の評価も「余裕を作っちゃいけない」というイメージであっさり解けてしまいました. かかった時間何と15分. さすがに誤読やミスを疑います. あわよくば全完とか浮かれていました.
問3に移りますが実験をしてみてもなかなか本質的な情報にたどり着かない. 2の不安とほとんど三番級を解いたことがない($\Rightarrow$解けたことがない)不安でなかなか集中できないのも重なって結局2点どまりでした.
終わったあと日本チームで集まっても一人を除いて全員2完, 一人全完がいましたが... 2が簡単というのは満場一致なようで少し安心しました. また, 今日のセットで世界的に差がつかないであろうということは薄々気づいていたため, 明日が全てを決める, 春3日目のような漠然とした不安がありました.
Day2
- $BC=DE$なる凸五角形$ABCDE$の内部に点$T$があり, $TB=TD, TC=TE, \angle ABT=\angle TEA$をみたしている. 直線$AB$は直線$CD, CT$とそれぞれ点 $P, Q$で交わっており, $P, B, A, Q$はこの順に並んでいる. また, 直線$AE$は直線$CD, DT$とそれぞれ点$R, S$で交わっており, $R, E, A, S$はこの順に並んでいる. このとき, $P, S, Q, R$は同一円周上にあることを示せ.
- $p$が素数であるような正の整数の組$(a, b, p)$であって, $a^p=b!+p$をみたすものをすべて求めよ.
- $n$を正の整数とする. 「北欧風の地形」とは, 各マスに整数が$1$つずつ書き込まれているような$n\times n$のマス目であって, $1$以上$n^2$以下の整数が$1$つずつ書き込まれているようなものを指す. $2$つの相異なるマスが隣接するとは, それらのマスがある辺を共有することをいう. そして, あるマスが「谷」であるとは, 隣接するどのマスに書き込まれている数も, そのマスに書き込まれている数より大きいことをいう. さらに, 次の$3$つの条件をみたす$1$つ以上のマスからなるマスの列を「登山道」とよぶ.
- 列の最初のマスは谷である.
- 列において連続する$2$つのマスは隣接している.
- 列の各マスに書き込まれている数は狭義単調増加である.
各$n$に対して, 北欧風の地形における登山道の個数としてありうる最小の値を求めよ.
どこかで幾何が来ることはわかっていたのですがまさか1番級とは. 幾何を重点的に対策していただけに少々残念でした. 図を描くと合同, 共円, 相似, aminoの補題が綺麗に見つかり, 一瞬で解けました. 20分くらい. aminoに感謝です2.
そして問5. まさかの自分が一番好きなタイプの問題. 解けるかということ以上に嬉しさで飛び上がりそうでした(). $p$でのオーダーを考えたり大小評価をしていくと最終的に$a=p$が求まりました. 試しに$2$でのオーダーを考えるとそのまま綺麗に不等式が立つ. 途中の$v_2(n!)=n-\text{popcount}(n)$はOMCのおかげです. ここにきて役立ちました. 結果85分で解き終わりました.
そして3Cです. 実はこの問題, 最後15分までずっと解が$(2+\frac12)n^2+O(n)$になると思い込んでいました. 構成は市松模様で片方が小さくて片方が大きい, みたいな. もちろん解答の通りなかなか進捗が生まれません. 最後の最後に実は谷が一つで通ることに気づき, 構成を試みるも途中で時間切れ... もう少し早く気づけていればよかった.
Day2もDay1同様の結果だったため, チーム全体の雰囲気はかなり良い状態を保つことができました.
結果
結果は772771. 終った瞬間は正直少し金メダルも期待していたのですが, やっぱりかなり簡単な回でしたね. 来年までに3番級に立ち向かえる実力をつけていきたい.
コンテストの後
数学のことは全部忘れて観光や交流を楽しむことができました. ここら辺の話は財団の通信でまた.
IMO～ そしてこれから
IMOはこれで終わりではないです. むしろ来年こそが本番です. あと一年.
長い記事でしたが, 最後まで読んでいただきありがとうございます. 読んでいる人の競技数学のモチベーションが少しでもあがってくれていれば嬉しいです. ではまた.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
