なぜ正'フェルマー素数'角形は作図できるのか？
背景
この記事では、正3角形、正5角形、正17角形に代表される「正'フェルマー素数'角形」が定規とコンパスで作図できることを、正17角形などの具体的な場合を計算して示すのではなく「どうしてこんな芸当が可能なのか」に焦点を置いて解説していきます。
自然数$n$を使って$2^{2^n} + 1$で表される素数をフェルマー素数という。
ある数が有理数と四則演算・平方根を有限回つかって表せるとき、作図できるという。
この「作図できる」の定義は、定規とコンパスで作図できることを示しています。
この記事は群・環・体のことばを使わずに書いているため、それらが分かっている方には冗長な言い回しが含まれます。
準備
正素数角形が作図できるか判断するために必要な道具を整理します。
素数を法とする原始根
素数で割った余り、いわゆる$\text{mod}$に注目します。この節でカギとなるのは「必ず原始根が存在し、原始根のべき乗ですべての数を表現できること」です。
互いに素な自然数$p, k$について、$k^{a} ≡ 1 \pmod p$が成り立つような最小の$a$が$φ(p)$と等しいとき、$k$をpを法とする原始根という。一般に、原始根は(存在する場合)複数存在する。
ここで、$φ(p)$は「$p$と互いに素な$p$未満の自然数の個数」であり、特に$p$が素数なら$p - 1$と等しい。
$p$が素数のとき、$p$を法とする原始根が必ず存在する。
素数$p$を法とする原始根$k$は「$(p - 1)$乗してはじめて$1$になる数」と説明することもできます。この性質から、$k$を順番に掛けていくと$2$から$p-1$までの数を1回ずつ通って$1$にたどり着き、それ以降は最初からループすることが分かります。たとえば$7$を法とする原始根として$3$がとれますから、次のような巡回が成り立ちます。
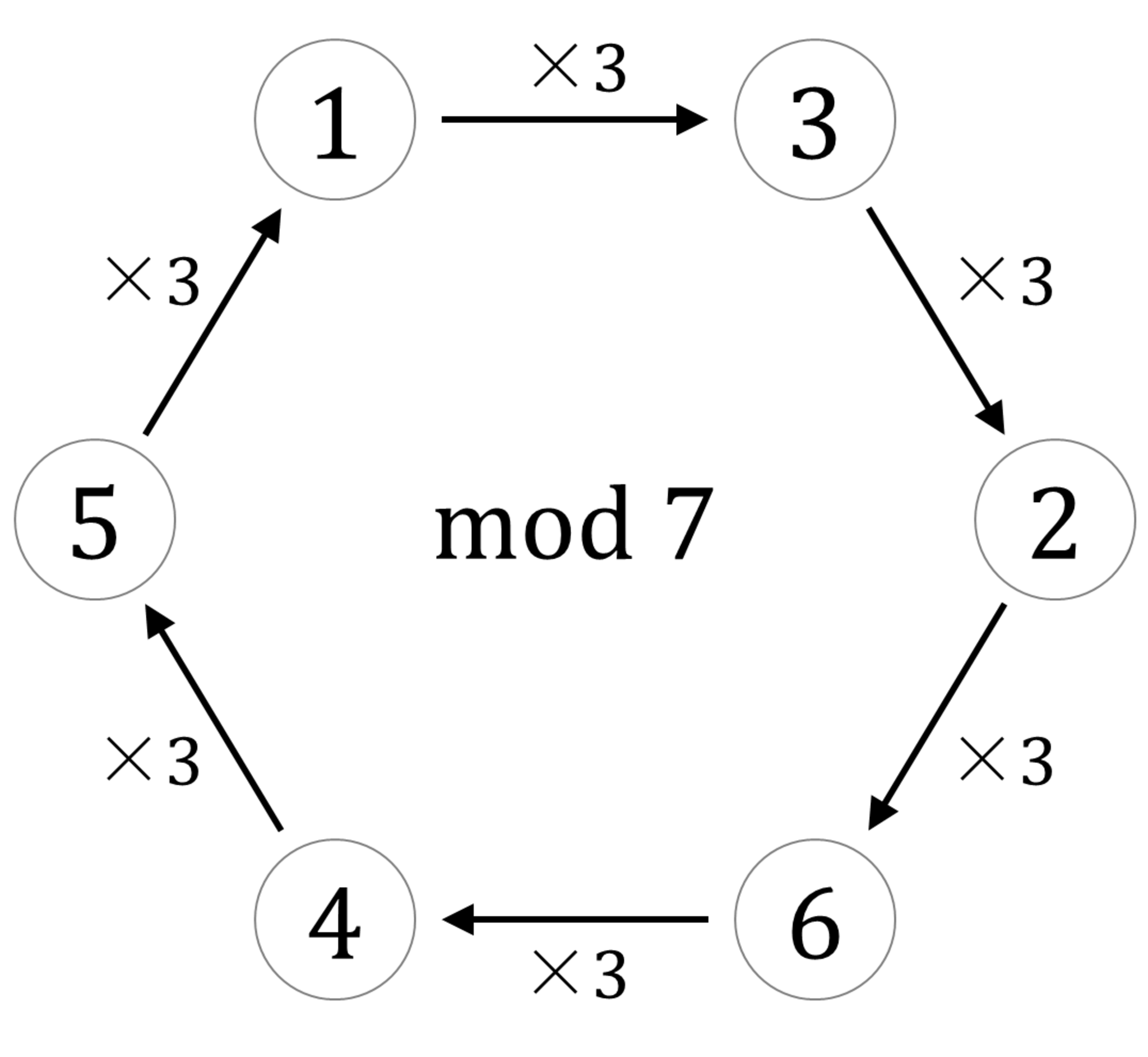7を法とする数の巡回
どの数から始めても3倍、3倍と繰り返し$3$を掛けていくことで、$7$未満の自然数を巡回することができます。この「掛け算による巡回」がのちのち役に立つので覚えておきましょう。
1のべき乗根
次に、1のべき乗根について必要な情報を整理します。
ある自然数$p$について、$z^p = 1$が成り立つような数$z$を1のp乗根という。
1のp乗根$z$について、$z^a = 1$が成り立つ最小の$a$が$p$と等しいとき、$z$を1の原始p乗根という。
$z$が1の原始p乗根であるとき、すべての1のp乗根は$z$のべき乗として表現できる。
$p$が素数のとき、1を除く1のp乗根はすべて原始p乗根である。
通常は、そしてこの記事でも1のp乗根は複素数の範囲で考えます。1のp乗根は、複素平面上では原点を中心に正p角形状に並びます。また、ド・モアブルの定理より
$$
ζ := \cos\dfrac{2π}{p} + i \sin\dfrac{2π}{p}
$$
とすると、この$ζ$は1の原始p乗根になります。
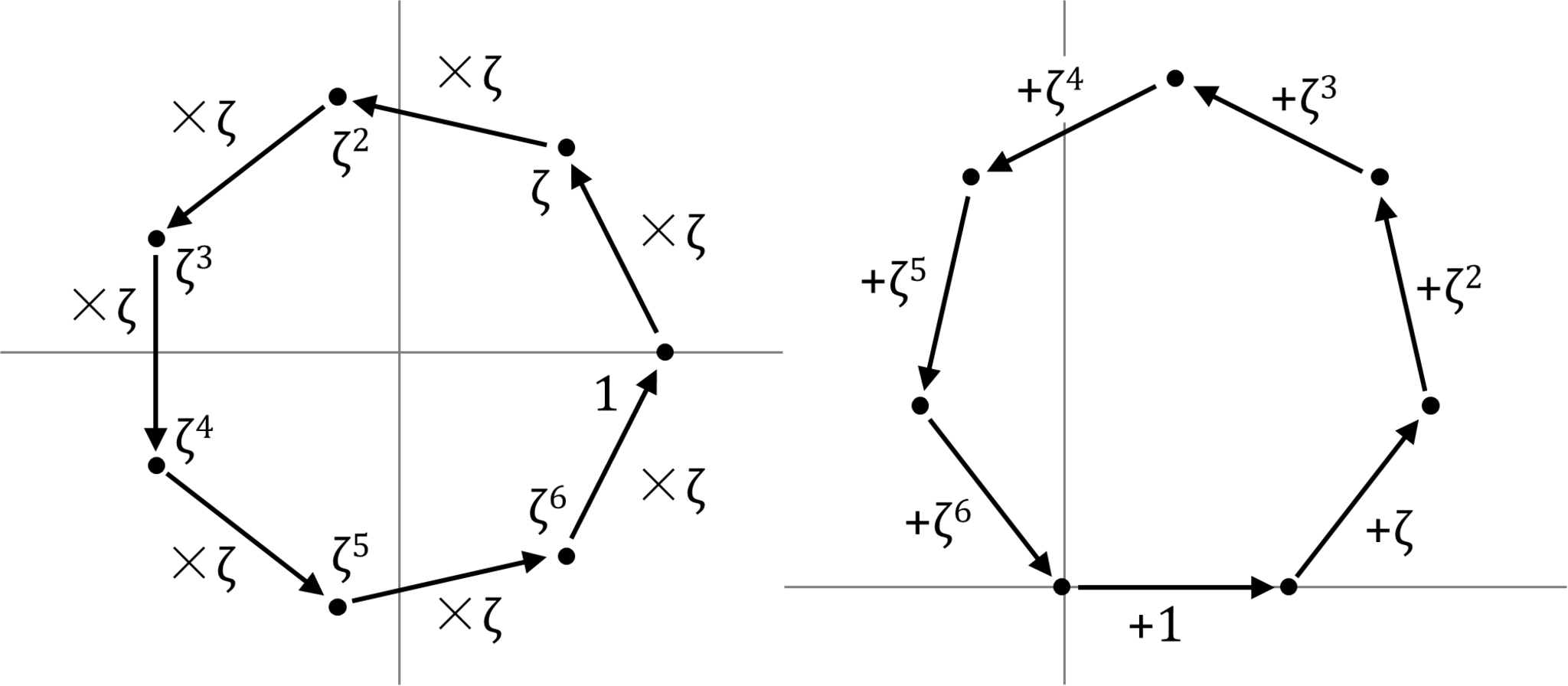複素平面における1の7乗根(左)とその和(右)
また、上図右のように複素平面上で1のp乗根を順番に足していくと正p角形を作り、元の場所に戻ってきます。1のp乗根のうちひとつは必ず1ですから、次のような定理が成り立ちます。
1の原始p乗根$ζ$について、次が成り立つ。
$$
ζ + ζ^2 + ζ^3 + ... + ζ^{p-1} + 1 = 0
$$
pを法とする原始根と1のp乗根
素数$p$を法とする原始根$k$のべき乗は、$p$未満のすべての自然数を一回ずつ通ることを示しました。ここから次の定理が成り立ちます。
$p$を素数とする。$p$未満の自然数$m$は、$p$を法とする原始根$k$と$p$未満の自然数$n$を使って次のように表せる。
$$
k^n ≡ m \pmod p
$$
また、1の原始p乗根の周期性を考えると、次が成り立ちます。
1の原始p乗根$ζ$と整数$a, b$について、
$$
a ≡ b \pmod p ⇔ ζ^a = ζ^b
$$
この2つを組み合わせて考えると次のような定理が成り立ちます。
$p$を素数とする。1を除くすべての1のp乗根を、$p$を法とする原始根$k$と原始p乗根$ζ$を使って次のように表すことができる。
$$
ζ^{k^1}, ζ^{k^2}, ζ^{k^3}, ... , ζ^{k^{p-1}}
$$
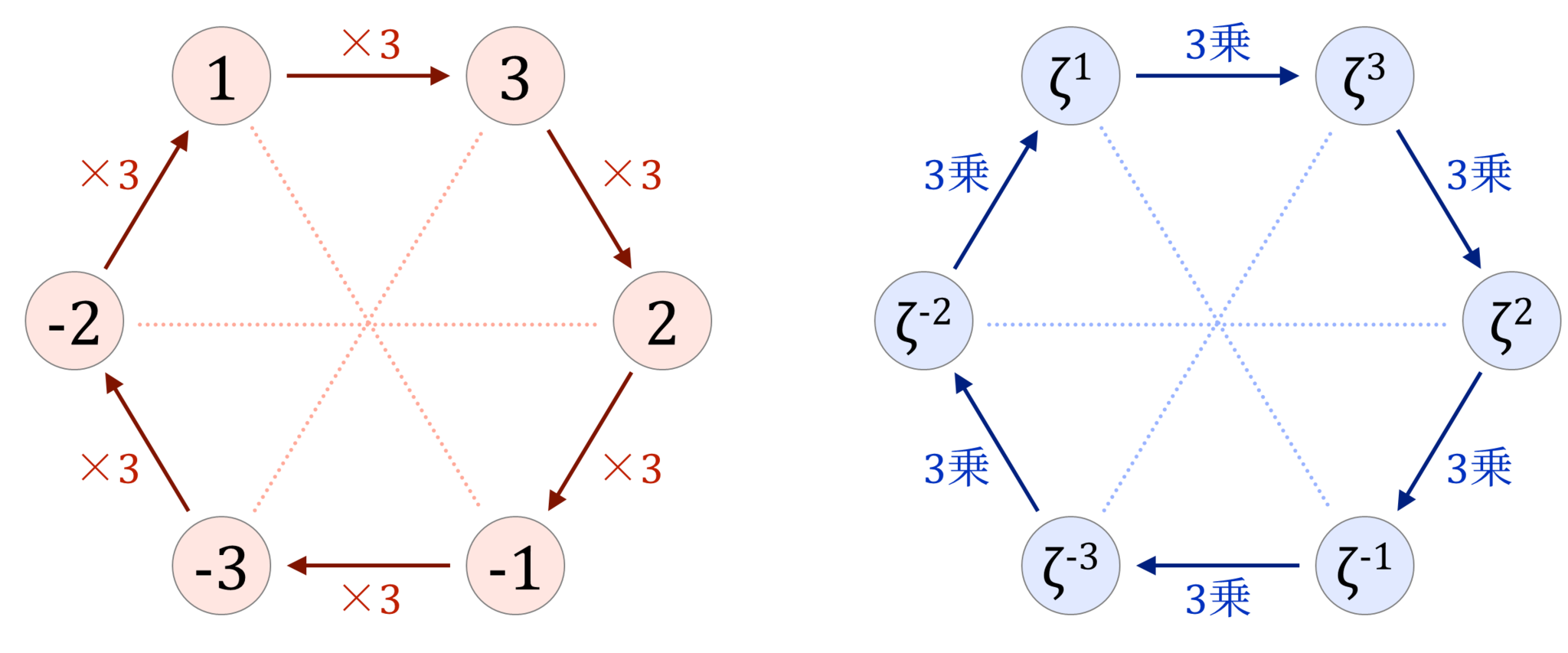
たとえば$p = 7$なら次のような'ループ'が作れます。
7を法とする数の巡回と1の原始7乗根
mod 7 の世界で繰り返し3を掛けることで1～6を巡回できたように、1の7乗根は繰り返し3乗することで$ζ^1$～$ζ^6$を巡回できるのです。整数のループには$0$が、p乗根のループには$ζ^0 = 1$が含まれないため、周期は$p - 1$となります。さらに、原始根の存在定理によりこのループは$p$がどんな素数でも作ることができます。
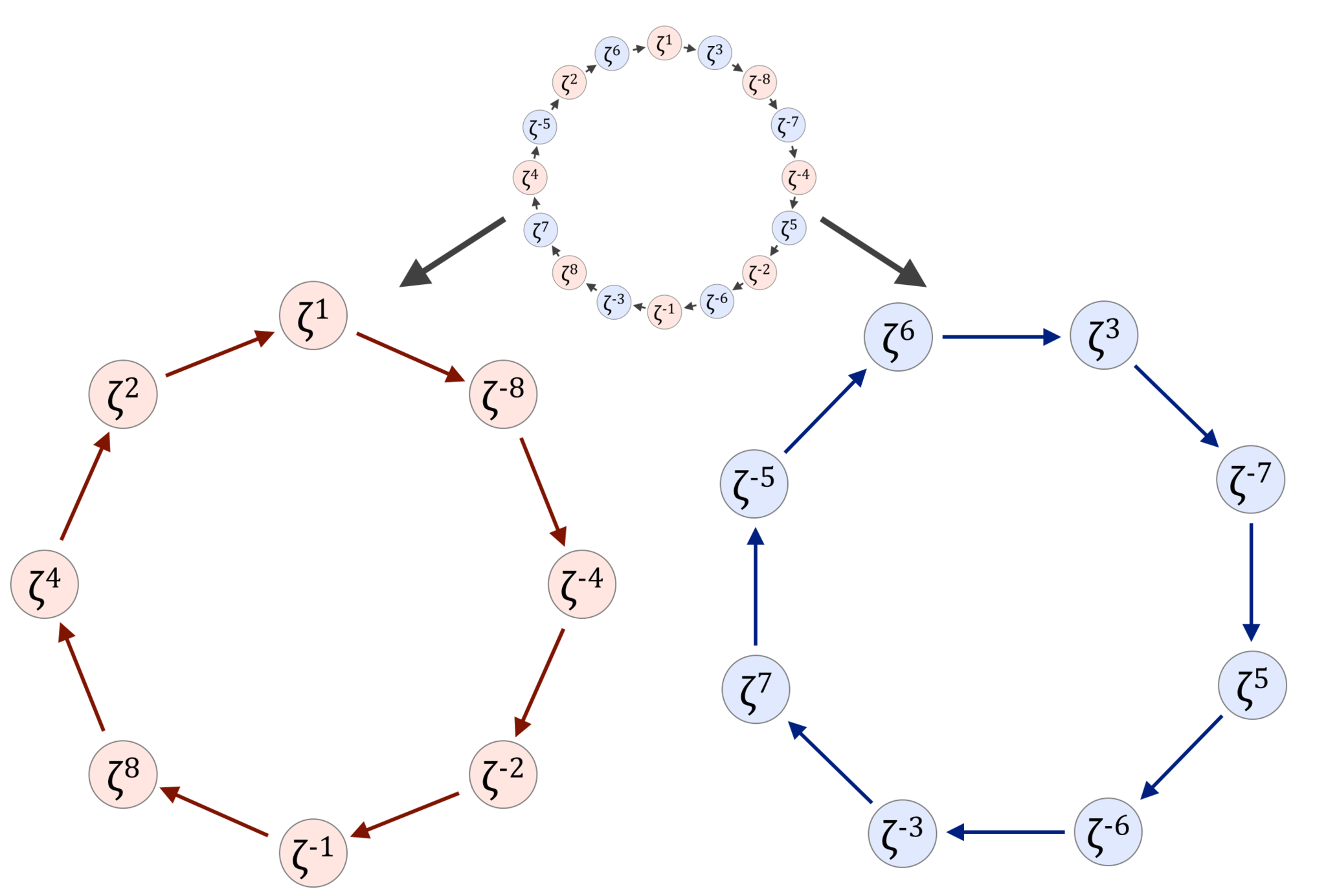
また、(どのような素数$p$と原始根$k$の組み合わせでも)このループの反対側にあるp乗根同士をかけ合わせると必ず$1$になります。下図のように負の指数を使うと、このことが分かりやすくなります。
7を法とする数の巡回と1の原始7乗根(負の指数を使った表現)
正'フェルマー素数'角形が作図できることの証明
定義と準備
ここからがいよいよ本題です。登場人物は次の3人です。
- フェルマー素数$p$
- $p$を法とする原始根$k$
- 1の原始p乗根$ζ := \cos\dfrac{2π}{p} + i \sin\dfrac{2π}{p}$
正p角形が作図できることを証明するためには$\cos\dfrac{2π}{p}$が有理数と四則演算・平方根で計算できることを示せばよいのですが(この2つは同値です。この記事を読んでいる方にとっては既知の事実でしょう)、この値は原始p乗根と次のような関係があります。
$$
\begin{align*}
ζ + ζ^{-1} &= (\cos\dfrac{2π}{p} + i \sin\dfrac{2π}{p}) + (\cos\dfrac{2π}{p} - i \sin\dfrac{2π}{p}) \\
&= 2 \cos\dfrac{2π}{p}
\end{align*}
$$
これにより、正p角形が作図できることと$ζ + ζ^{-1}$が作図できることは同値であることが分かりました。よって、ここからは$ζ + ζ^{-1}$が二次方程式を連鎖的に解いて求められることを証明していきます。
ようやく正p角形と繋がりましたね。
p乗根のグループ分け
1を除く1のp乗根は$ζ^{k^1}, ζ^{k^2}, ζ^{k^3}, ... , ζ^{k^{p-1}}$と繰り返し$k$乗することで全て表すことができ、これは$p - 1$の周期で循環するループになっているのでした。$p = 17, k = 3$の場合は次のようになります。
1の17乗根の巡回
さて、このループは$p - 1$の周期で循環しますが、フェルマー素数の定義より$p - 1$は2のべき乗ですから必ず偶数周期のループになり、これを奇数番目の数と偶数番目の数に分けることで、周期が半分になったループを2つ作ることができます。新しくできたループはもとのループの「ひとつ飛ばし」ですから、すべての数がひとつ前の数の$k^2$乗になります。
1の17乗根のグループ分け
完成した2つのループについて、それぞれの数の和を$α_1, α_2$とおくと、$α_1, α_2$を解に持つ有理数係数の二次方程式が必ず立てられます。具体的には、1のp乗根の性質から$α_1 + α_2 = -1$が分かり、$α_1α_2$を計算すると有理数になるので、解と係数の関係を使って二次方程式を立てることができます。
二次方程式 $x^2 + ax + b = 0$の解を$α,β$とすると、
$$
\begin{align*}
α + β &= -a \\
αβ &= b
\end{align*}
$$
が成り立つ。
計算すると$α_1α_2 = -4$になるので、二次方程式$x^2 + x - 4 = 0$を解いて$α_1,α_2 = \dfrac{-1 \pm \sqrt{17}}{2}$となります。どちらがどの符号をとるかは、コサインの大小関係から決められます(上図のようにグループ分けしたなら、左側がプラスの符号をとります)。
「二次方程式が必ず立てられる」ことを証明するには体の拡大などの知識が必要で、その解説にはこの記事と同じくらいの長さが必要なので詳細は 別の記事 に分けます。
$α_1, α_2$は有理数を係数とする二次方程式の解ですから、有理数と四則演算・平方根を使って表すことができます。なお、$p = 5$の場合はここで求めた値の片方が$ζ^1 + ζ^{-1} = 2\cos\dfrac{2π}{5} = \dfrac{\sqrt{5} - 1}{2}$になるので、ここで証明終了です。
再帰的なグループ分け
周期$\dfrac{p - 1}{2}$で循環する2つのループができ、それぞれが含む数の和が二次方程式の解として求められました。できあがったループの周期が2より大きいなら、さらに奇数番目と偶数番目に分けることで周期$\dfrac{p - 1}{4}$のループを計4つ作ります。
1の17乗根のグループ分け2回目
和が$α_1$のループから作った小さなループの数の和を$β_1, β_2$、和が$α_2$のループから作った小さなループの数の和を$β_3, β_4$とすると、「$β_1, β_2$を解に持つ二次方程式」と「$β_3, β_4$を解に持つ二次方程式」を立てることができます。これらの二次方程式の係数は有理数と$α_1, α_2$の四則演算だけで表すことができ、やはり作図できます。
以降、これと同じことを周期2のループができるまで再帰的に繰り返します。1段階進むごとにループの周期は半分になり、ループと二次方程式の数が倍に増えていきます。周期2のループは必ず$ζ^n$と$ζ^{-n}$の組み合わせになるので、この時点で$ζ^1 + ζ^{-1}$の値が求められて証明終了です。
しつこいようですが、フェルマー素数から$1$を引くと$2$のべき乗になるので「周期を半分にするグループ分け」の繰り返しは必ず周期2のループにたどり着きます。
見通しをよくするために、最後までセットで扱う数の和を$θ_n := ζ^n + ζ^{-n}$と書くことにします。$θ_aθ_b = θ_{a + b} + θ_{a - b}$が成り立つため計算もしやすいです。
前のステップで周期8のループを作り、次の値を求めました。
$$
\left\{
\begin{align*}
α_1 = θ_1 + θ_8 + θ_4 + θ_2 &= \dfrac{-1 + \sqrt{17}}{2} \\
α_2 = θ_3 + θ_7 + θ_5 + θ_6 &= \dfrac{-1 - \sqrt{17}}{2}
\end{align*}
\right.
$$
さらに$α_1,α_2$のループを奇数番目と偶数番目にグループ分けして周期4のループを作り、それぞれのループの和を
$$
\left\{
\begin{align*}
β_1 &= θ_1 + θ_4 \\
β_2 &= θ_8 + θ_2 \\
β_3 &= θ_3 + θ_5 \\
β_4 &= θ_7 + θ_6
\end{align*}
\right.
$$
とすると、$β_1β_2 = β_3β_4 = -1$になるので、これらの値を使って二次方程式を立てます。
- $β_1 > β_2$は$x^2 - α_1x - 1 = 0$の解
- $β_3 > β_4$は$x^2 - α_2x - 1 = 0$の解
さらにグループ分けをして周期2のループを作ります。例えば$β_1$のループは$θ_1$と$θ_4$に分けられます。同じように$θ_1θ_4$などを計算すると次の方程式が立てられます。
- $θ_1 > θ_4$は$x^2 - β_1x + β_3 = 0$の解
- $θ_8 < θ_2$は$x^2 - β_2x + β_4 = 0$の解
- $θ_3 > θ_5$は$x^2 - β_3x + β_2 = 0$の解
- $θ_7 < θ_6$は$x^2 - β_4x + β_1 = 0$の解
「正17角形が作図できること」を証明するならここまでで十分ですが、せっかくなので$θ_1 = 2\cos\dfrac{2π}{17}$の値を求めてみます。必要な方程式をすべて解くと、
$$
\begin{align*}
θ_1 &= ζ^1 + ζ^{-1} = 2\cos\dfrac{2π}{17} \\
&= \dfrac{-1 + \sqrt{17} + \sqrt{34 - 2\sqrt{17}} + 2\sqrt{17 + 3\sqrt{17} - \sqrt{34 - 2\sqrt{17}} - 2\sqrt{34 + 2\sqrt{17}}}}{8}
\end{align*}
$$
となり、確かに$\cos\dfrac{2π}{17}$が有理数と四則演算・平方根の組み合わせで表せることが分かります。