なぜ1の'フェルマー素数'乗根は二次方程式を連鎖的に解いて求められるのか
この記事は「 なぜ正'フェルマー素数'角形は作図できるのか？ 」の発展的な内容として書いています。
この記事の作者は体初心者ですので、間違いがあればご指摘ください。
基本的なアイデア
正p角形が作図できるか考える問題は$\cos\frac{2π}{p}$が作図できる(有理数と四則演算・平方根の組み合わせで表せる)か考えることと同値で、1のp乗根が作図できるかを考えることでこれが求められます。しかし、ある未知数が作図できるかを直接調べるのは大変です。有理数は四則演算に対して閉じていますが、平方根に対しては閉じていないことがこの問題を複雑にしています。
そこで、演算が閉じていない平方根を任意の数に使うことは封じて、有理数と「ある二次方程式の解」の四則演算でどんな数が表現できるかを考えます。これは定義上作図できることが分かっていますし、未知数が作図できるか調べるよりも簡単です。
この記事で解説するのは後者のアイデアで、「体の拡大」と呼ばれます。
体の拡大
適切な四則演算が定義されていて、かつ四則演算に対して($0$で割ることを除いて)閉じているような構造を体(たい、field)という。
たとえば有理数全体は体をなし、それを有理数体$\mathbb{Q}$と表します。
「適切な四則演算」には厳密な定義がありますが、この記事では有理数と実数の四則演算が体の定義を満たしていることが分かっていれば十分です。また、体の定義にべき乗根は含まれていないことも覚えておきましょう。
有理数体$\mathbb{Q}$に$\sqrt2$を追加して「有理数・$\sqrt2$・四則演算で表せるすべての数を含む集合」を考えてみます。この集合は明らかに四則演算に対して閉じているので再び体をなします。
このような操作を有理数体$\mathbb{Q}$に$\sqrt2$を添加するといい、できあがる体を拡大体とよんで$\mathbb{Q}(\sqrt2)$と表します。またこの操作自体のことを拡大とよび、$\mathbb{Q}(\sqrt2)/\mathbb{Q}$で表します。
$\mathbb{Q}(\sqrt2)$はすべての有理数に加えて$1 + \sqrt2$や$5\sqrt2$などの無理数を含みますが、実数全体ほど多くの数は含みません。たとえば$\sqrt3$や$\sqrt2 + \sqrt5$のような数は、有理数・$\sqrt2$・四則演算をどのように組み合わせても表すことができません。
この体が含んでいるのは次の定理に示すような形で表せる数だけです。
$n$を2乗数ではない整数とする。体$\mathbb{Q}(\sqrt{n})$に含まれるすべての数は、2つの有理数$a,b \in \mathbb{Q}$を使って$a + b\sqrt{n}$と表すことができる。
実際に、$a + b\sqrt{n}$と$c + d\sqrt{n}$ ($a,b,c,d \in \mathbb{Q}$) の四則演算を考えると
$$
\begin{align*}
(a + b\sqrt{n}) + (c + d\sqrt{n}) &= (a + c) + (b + d)\sqrt{n} \\
(a + b\sqrt{n}) - (c + d\sqrt{n}) &= (a - c) + (b - d)\sqrt{n} \\
(a + b\sqrt{n})(c + d\sqrt{n}) &= (ac + bdn) + (ad + bc)\sqrt{n} \\
\dfrac{a + b\sqrt{n}}{c + d\sqrt{n}} &= \dfrac{ac - bdn}{c^2 - d^2n} + \dfrac{bc - ad}{c^2 - d^2n}\sqrt{n}
\end{align*}
$$
となり、すべて有理数$x,y \in \mathbb{Q}$を使って$x + y\sqrt{n}$の形で表せることが分かります。やや乱暴な言い方をすれば、この表現方法が「四則演算に対して閉じている」ことを示しています。
拡大の次数
$\mathbb{Q}(\sqrt{n})$のすべての数は$x + y\sqrt{n}$という形で表せました。同じようなことを他の体の拡大についても考えることができます。
体$E$とその拡大体$F$について、$e_0,e_1,...,e_n$を$E$の元、$f_1,f_2,...,f_n$を$E$に含まれない$F$の元とすると、$F$のすべての元を次の形で表すことができる。
$$
e_0 + e_1f_1 + e_2f_2 + ... + e_nf_n
$$
ここで、$f_1,f_2,...,f_n$を適切な元で固定したときに$F$のすべての元を表現できるような最小の項の数を拡大の次数という。
また、次数が$n$であるような拡大を$n$次拡大という。
ここまでで見てきたように$\mathbb{Q}(\sqrt{n})$に含まれるすべての数は$a + b\sqrt{n}\ (a,b \in \mathbb{Q})$という形で表せます($a,b$は$e_0,e_1$にあたり、$\sqrt{n}$は固定された$f_1$にあたります)。この式の項の数は2で、これ以上少ない項の数で$\mathbb{Q}(\sqrt{n})$のすべての数を表すことはできませんから、$\mathbb{Q}(\sqrt{n})/\mathbb{Q}$の次数は$2$です。
また、$e_0 + e_1f_1 + e_2f_2 + ... + e_nf_n$という元の表し方を$(e_0, e_1,...,e_n)$という元の順序対と考えると、これはベクトルの定義を満たします。
体$E$とその拡大体$F$について、$F$は$E$を係数とするベクトル空間をなす。
このとき、ベクトル空間の次元と拡大の次数が一致する。
ついでのようにベクトル空間をなすことを示しましたが、これが重要な役割を果たします。
拡大と方程式
この節では未知の値を添加する拡大について考えます。
さっそくですが、次の定理が成り立ちます。
体$E$とその$n$次拡大体$F$があったとき、任意の$x \in F$に対して少なくともひとつは$0$でない$e_0,e_1,...,e_n \in E$が存在し、次の式を満たす。
$$
e_0 + e_1x + e_1x^2 + ... + e_nx^n = 0
$$
言い換えると、任意の$x \in F$は必ず$E$を係数とする$n$次方程式の解になる。
ここでいう$n$次方程式は広義の$n$次方程式であり、次数が$n$以下の方程式のことをいいます。
$n + 1$個の$F$の元$f_0, f_1, ..., f_n$を考える。
$F$は$E$を係数とする$n$次元ベクトル空間をなすから、$n$個を超える$F$の元は必ず一次従属になる。
よって、次の式を満たすような少なくともひとつは$0$でない$e_0,e_1,...,e_n \in E$が存在する。
$$
e_0f_0 + e_1f_1 + e_1f_2 + ... + e_nf_n = 0
$$
この$f_0, f_1, ..., f_n$に$1, x, x^2, ..., x^n$を代入すると与式が得られる。
定理4は、ある数が作図できるか考える上でとても重要です。
$\mathbb{Q}$にどんな数を添加したか分からなくても、それが2次拡大ならただちに「二次方程式を解いて求められる」ことが分かるからです。また、「繰り返し二次方程式を解いて得られる数」は「有理数体$\mathbb{Q}$を繰り返し2次拡大した体」に含まれることも分かります。
円分体
いよいよ本題、1の原始p乗根について考えていきましょう。体の世界では、有理数全体に1の原始p乗根を添加した拡大体を円分体と呼びます。
なお、断りがない限り$p$は$3$以上の素数、$ζ$は1の原始p乗根とします。
有理数体$\mathbb{Q}$に1の原始p乗根$ζ$を添加した拡大体$\mathbb{Q}(ζ)$を円分体という。
原始p乗根については 元の記事 をご覧ください。
まずは拡大の次数を考えます。任意の$x \in \mathbb{Q}(ζ)$は、有理数$a_0,a_1,...,a_{p - 1} \in \mathbb{Q}$を使って次のように表せそうです。
$$
x = a_0 + a_1ζ + a_2ζ^2 + ... + a_{p-1}ζ^{p-1}
$$
しかし原始p乗根は
$$
1 + ζ + ζ^2 + ... + ζ^{p - 1} = 0
$$
を満たすという性質がありますから、もとの式から原始p乗根のうち任意のひとつを省いて、次のような式に変形することができます(省いた原始p乗根を$ζ^n$とします)。
$$
x = (a_0 - a_n) + (a_1 - a_n)ζ + (a_2 - a_n)ζ^2 + ... + (a_{p-1} - a_n)ζ^{p-1}
$$
2つ以上の原始p乗根を省くことはできません。よって、この拡大の次数は$p-1$になります。拡大の次数と方程式の次数は対応していますから、これで1の原始p乗根は多くとも$p - 1$次の方程式の解になることが分かります。……これではまだ作図できるか判断できそうにありませんね。
$\mathbb{Q}(ζ)/\mathbb{Q}$の中間体
方程式を解く都合上、いきなり大きな次数の拡大を扱うのは大変ですから、より小さな次数の拡大に分解することを考えたくなります。このような「拡大の分解」を考えたとき、元の体と拡大体の間に挟まる体を中間体とよびます。
体$E$から体$F$への拡大$F/E$に対して、$M$が$E$の拡大体であって、$F$が$M$の拡大体であるような体$M$が存在するとき、この体$M$を拡大$F/E$の中間体という。
幸いなことに、ガロア理論の知識を使うと次の定理が成り立つことが分かります。これを証明することは難しいので、ありがたく結論だけを使わせてもらいましょう。
$p$が$3$以上の素数で$ζ$を1の原始p乗根とすると、有理数体から円分体への拡大$\mathbb{Q}(ζ)/\mathbb{Q}$には$p - 1$の約数と一対一で対応する中間体が存在する。
ここで、$p-1$の約数$n$に対応する中間体を$D_n$と表すことにすると、$m$が$n$を割り切るとき$D_n$は$D_m$の$\frac{n}{m}$次拡大体となる。
言葉だけでは少し分かりにくいので、$P=13$の例を図で示します。$\mathbb{Q}$は$1$に、$\mathbb{Q}(ζ)$は$12$にそれぞれ対応しています。
1の原始13乗根ζに至る拡大ルート
これによって、有理数体から円分体への拡大の次数が「素因数分解」できることが分かります。上図のように$p = 13$であれば$13 - 1 = 2^2×3$ですから、$ζ$を含む体$\mathbb{Q}(ζ)$を得るためには有理数体$\mathbb{Q}$から始めて2次拡大→2次拡大→3次拡大と3回拡大すればよいわけです。
$p = 17$とすれば$17 - 1 = 2^4$ですから、有理数体$\mathbb{Q}$に4回の2次拡大を施せばいいことが分かります。定理4より、2次拡大で得られる数はすべて2次方程式の解として得られますから、$ζ$が(実際に値を求めなくても)作図できることが分かります。
抽象的に考えていると忘れがちですが、各中間体も有理数体$\mathbb{Q}$になんらかの数を添加して得られる拡大体です。このとき添加される数は、実は元の記事で求めていました。$ζ$のループをいくつかにグループ分けしたときの各ループの和が「添加される数」にあたります。
$p = 17$のときの「
最初のグループ分け
」で考えてみましょう。
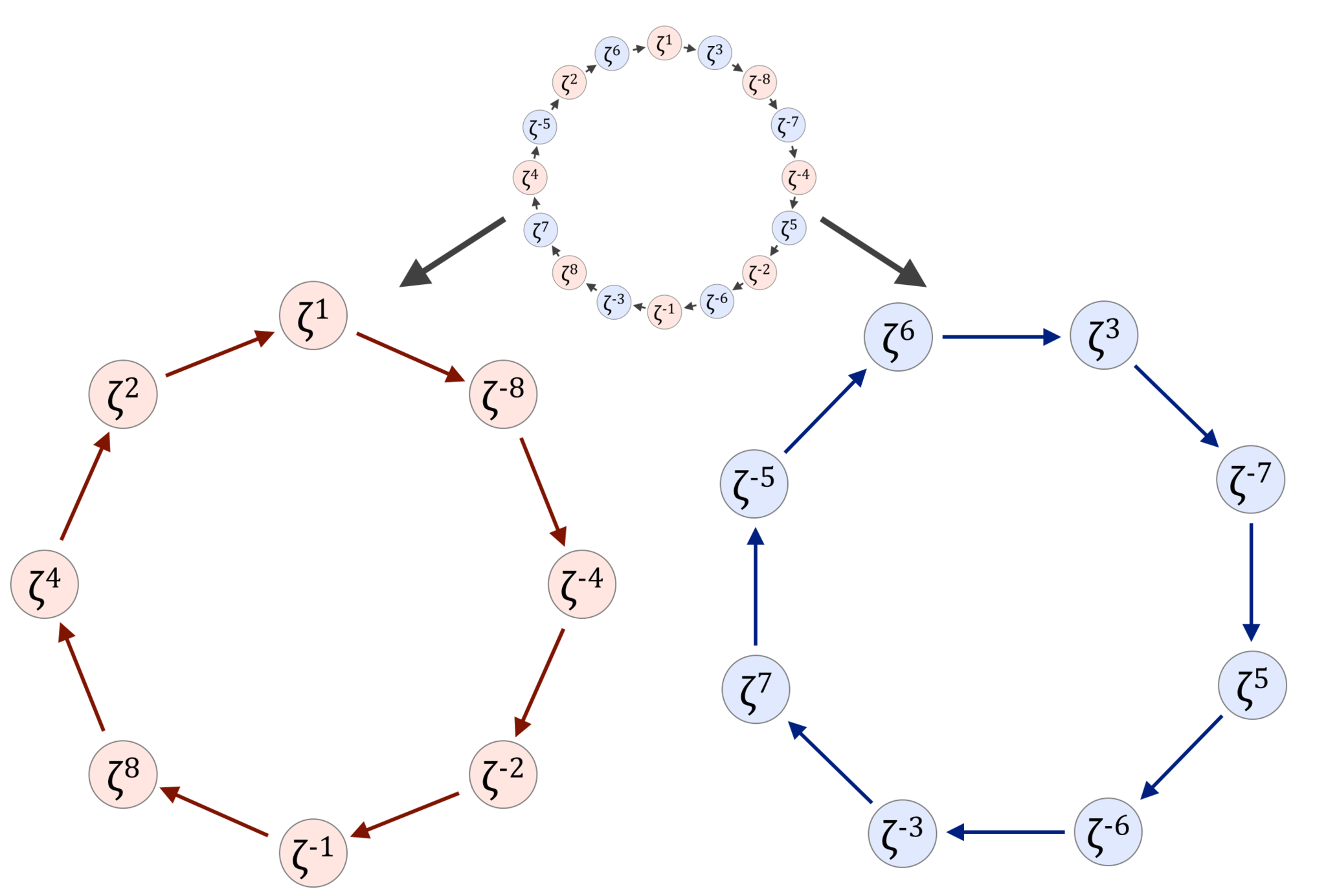1の17乗根のグループ分け
$$
\begin{align*}
a_1 &= ζ^1 + ζ^{-8} + ζ^{-4} + ζ^{-2} + ζ^{-1} + ζ^8 + ζ^4 + ζ^2 \\
a_2 &= ζ^3 + ζ^{-7} + ζ^5 + ζ^{-6} + ζ^{-3} + ζ^7 + ζ^{-5} + ζ^3
\end{align*}
$$
とします。$α_1 + α_2 = -1$が成り立ちますから、$α_2$を$-1 - α_1$と表せば添加する数はひとつで済みます。$\mathbb{Q}(α_1)$を考えると、$α_1$と有理数の四則演算で得られる数は、$ζ$を使わずに$α_1$と有理数だけで表せることが分かります。この体は$D_2$であり、「$2$つ」にループを分けたこと、$16$の約数「$2$」と対応しています。
まとめ
情報の整理
情報量が多くなってきたので、元の記事の内容とあわせて整理します。素数$p$に対して、様々な概念が$p - 1$という数やその約数を通して繋がっていることが分かるでしょうか。
3以上の素数$p$、$p$を法とする原始根$k$、1の原始p乗根$ζ$について、次の概念が$p-1$という数を通して対応しています。
- $p$以下の任意の自然数を$k^n \pmod p$で表現でき、$p - 1$周期のループが作れる
- 1のp乗根すべてを$ζ^{k^n}$で表現でき、$p - 1$周期のループが作れる
- 拡大$\mathbb{Q}(ζ)/\mathbb{Q}$の次数は$p - 1$である
また、次の概念もそれぞれ対応しています。
- $p - 1$の約数$n$
- $ζ$のループを$n$個に分けたときの、各ループの和
- $\mathbb{Q}$の$n$次拡大で得られる$\mathbb{Q}(ζ)/\mathbb{Q}$の中間体$D_n$
そして忘れてはいけないのが、
$$
ζ^1 + ζ^{-1} = 2\cos\dfrac{2π}{p}
$$
が成り立つことです。
この記事が示したかったこと
ごちゃごちゃしていますが結論はシンプルです。
正p角形を作図するために1の原始p乗根が作図できるか調べたいのですが、そのままでは$p - 1$次方程式を解かなければならず、求めるのが困難でした。
体の拡大と方程式の対応
しかし、体の考え方とガロア理論を使うことで「そこに至るルート」を作ることができ、$p$が$2^n + 1$の形で表せる素数なら作図できる、ということが簡単に示せるようになりました。
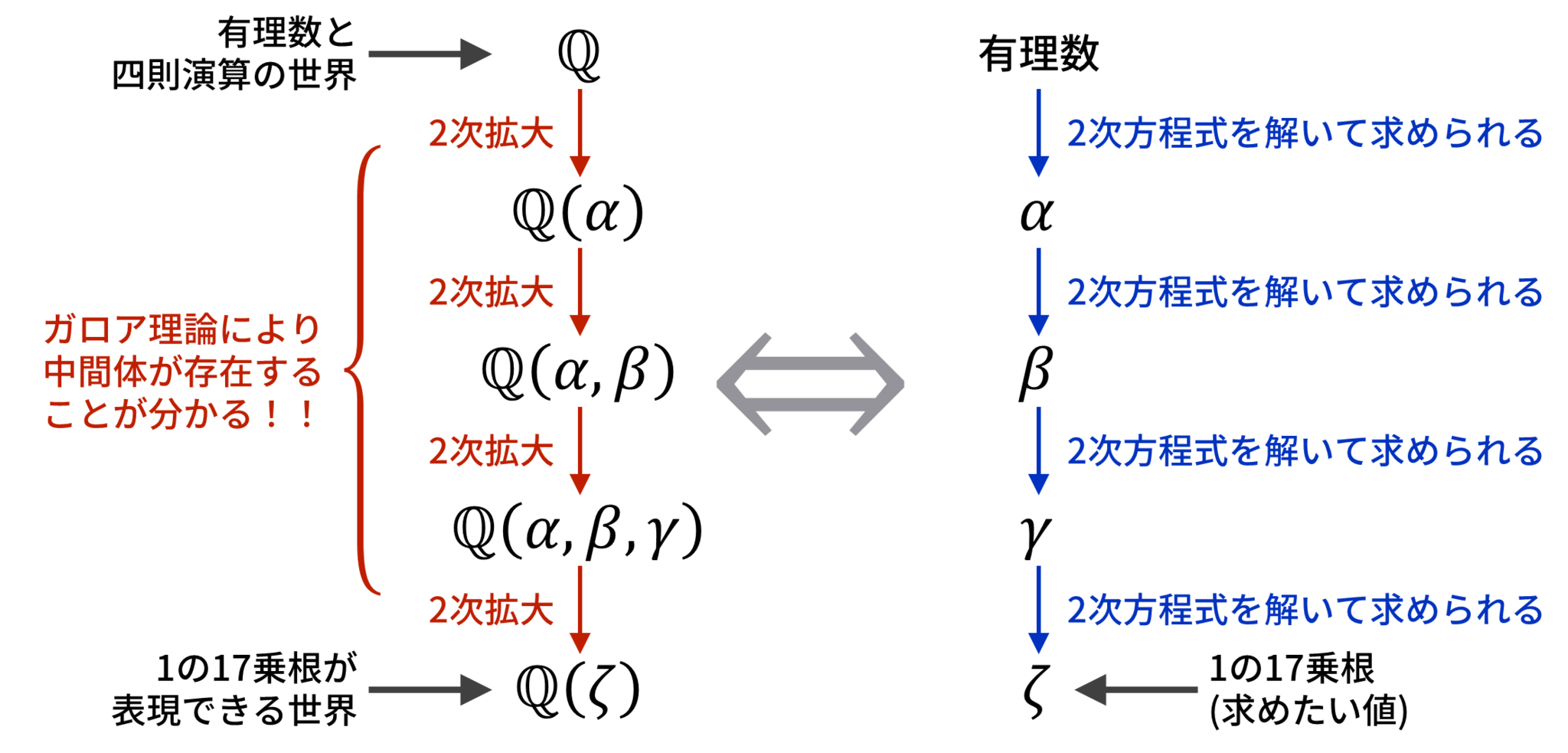中間体による「方程式のルート」
最終的に、ある素数$p$に対して、正$p$角形が作図できるか判断するには、単に$p - 1$を素因数分解してみて、そこに$2$以外の素因数が含まれていないことを確認すればよいということになります。
折り紙による作図は四則演算・平方根に加えて立方根も使えますが、この場合も$p - 1$の素因数が$2$と$3$だけであれば作図できる、ということが分かりますね。
