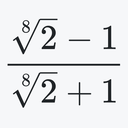cos ln tan θ の積分

\begin{eqnarray} {\rm B}(x,y) &=& 2\int_0^\frac\pi2 (\sin\theta)^{2x-1}(\cos\theta)^{2y-1}d\theta \\ \int_0^\frac\pi2(\tan\theta)^z d\theta &=& \frac1{2}{\rm B}\left(\frac{1+z}2,\frac{1-z}2\right) \\&=& \frac{\Gamma \left(\frac{1+z}2\right)\Gamma \left(\frac{1-z}2\right)}{2\Gamma(1)} \\&=& \frac\pi2\csc\frac{\pi(1+z)}2 \\&=& \frac\pi2\sec\frac{\pi z}2 \\ \frac\pi2{\rm sech}\frac{\pi z}2 &=& \frac\pi2\sec\frac{\pm\pi iz}2 \\&=& \frac\pi4\left(\sec\frac{\pi iz}2 + \sec\frac{-\pi iz}2\right) \\&=& \frac1{2}\int_0^\frac\pi2\lbrace(\tan\theta)^{iz}+(\tan\theta)^{-iz}\rbrace d\theta \\&=& \int_0^\frac\pi2\cos(z\ln\tan\theta) d\theta \end{eqnarray}