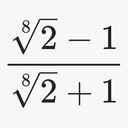3F2と2F1の有限和の恒等式
$\displaystyle \sum_{k=0}^{n} (-4)^k\binom{n}{k}\frac{(a,b)_k}{(a+b)_{2k}} = \sum_{k=0}^{2n} (-2)^k\binom{2n}{k}\frac{(a)_k}{(a+b)_k} $
$(a_1,\cdots,a_j)_n \coloneqq (a_1)_n\cdots(a_j)_n$と略記します。
超幾何級数を使うとこのようになります。
$\displaystyle
\hygeo3F2{a,b,-n}{\frac{a+b}2,\frac{a+b+1}2}1 =
\hygeo2F1{a,-2n}{a+b}2
$
$\beginend{eqnarray}{
\frac{{\rm B}(a+k,b+l)}{{\rm B}(a,b)} &=&
\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}
\frac{\Gamma(a+k)\Gamma(b+l)}{\Gamma(a+b+k+l)} \\&=&
\frac{(a)_k(b)_l}{(a+b)_{k+l}}
}$
$\beginend{eqnarray}{
\sahen &=&
\sum_{k=0}^{n} \binom{n}{k}\frac{{\rm B}(a+k,b+k)}{{\rm B}(a,b)}(-4)^k \\&=&
\frac{1}{{\rm B}(a,b)}\int_0^1 t^{a-1}(1-t)^{b-1}[1-4t(1-t)]^n dt \\&=&
\frac{1}{{\rm B}(a,b)}\int_0^1 t^{a-1}(1-t)^{b-1}\qty(1-4t+4t^2)^n dt \\&=&
\frac{1}{{\rm B}(a,b)}\int_0^1 t^{a-1}(1-t)^{b-1}(1-2t)^{2n} dt \\&=&
\sum_{k=0}^{2n} (-2)^k\binom{2n}{k}\frac{{\rm B}(a+k,b)}{{\rm B}(a,b)} \\&=&
\uhen
}$
$\beginend{align}{ \sum_{n=0}^\infty \frac{(a,b)_n}{(a+b)_{2n}}\lr({-\frac{4x^2}{1-x^2}})^n &= \frac12\sum_{n=0}^\infty \frac{(a)_n}{(a+b)_n} \qty[(1+x)\qty(-\frac{2x}{1-x})^n + (1-x)\qty(\frac{2x}{1+x})^n] \\&= \frac{1\pm x}2\sum_{n=0}^\infty \frac{(a)_n + (b)_n}{(a+b)_n}\lr({\mp\frac{2x}{1\mp x}})^n }$
$\beginend{align}{ &\because\\ &f(x) = \sum_{n=0}^\infty a_nx^n \\ &\Longleftrightarrow\\ &\frac1{1-x}f \lr({\frac{x}{1-x}}) = \sum_{n=0}^\infty \lr[{\sum_{k=0}^n \binom{n}{k}a_k}]x^n }$
これは超幾何関数を使うと
$\beginend{align}{
\hygeo3F2{a,b,1}{\frac{a+b}2,\frac{a+b+1}2}{-\frac{x^2}{1-x^2}} &=
\frac12\qty[(1+x)\hygeo2F1{a,1}{a+b}{-\frac{2x}{1-x}} + (1-x)\hygeo2F1{a,1}{a+b}{\frac{2x}{1+x}}] \\&=
\frac{1\pm x}2\lr({
\hygeo2F1{a,1}{a+b}{\mp\frac{2x}{1\mp x}} +
\hygeo2F1{b,1}{a+b}{\mp\frac{2x}{1\mp x}}})
}$
となります。
$\displaystyle \hygeo3F2{-n,b,c}{\frac{-n+b}2,\frac{-n+b+1}2}1 = \hygeo2F1{-n,2c}{-n+b}2 $
両辺が$c$についての多項式であり無限個の$c$で成り立つため常に等しい。