【Causality】時空が大域的に共形時間と空間に分解するための必要十分条件

安定的因果時空は強因果時空であることが示される（Mathpediaの記事参照）。

安定的因果時空の特徴付けから明らかである。

https://mathlog.info/articles/2906 の定理２の系参照。

　標準的定常時空ならば、定義より、関数$t\in C^\infty(M)$が存在して、$g=-\beta(x)^2dt^2+2\omega(x) dt+h(x)$と表される。${\rm grad}\ t$が過去向き時間的ベクトル場であることを示せすことが出来れば$t$は可微分時間関数となり、$(M,g)$は安定的因果時空となるから命題４より区分時空である。
　
　よって任意の未来向き因果的ベクトル$v$に対して、$g({\rm grad}\ t,v)>0$となることを示せば良い。$v$を$\partial_t$と$t$のレベル集合に接する方向に分解して$v=v^t\partial_t+v_x$とすれば、結局$v^t=g({\rm grad}\ t,v)>0$を示せば良い。

　$\partial_t$と$v$が共に未来向きであるから、
$$ \begin{align} g(\partial_t,v)=-\beta^2v^t+2\omega(v_x)\le0,\\ \therefore\ 2\omega(v_x)\le\beta^2 v^t \end{align} $$
である。

　また$v$は因果的であるから
$$ \begin{align} &||v||^2=-\beta^2(v^t)^2+2\omega(v_x) v^t+||v_x||^2_h\le0,\\ &v^t\le \frac{\omega(v_x)-\sqrt{\omega(v_x)^2+\beta^2||v_x||^2}}{\beta^2},\ \frac{\omega(v_x)+\sqrt{\omega(v_x)^2+\beta^2||v_x||^2}}{\beta^2}\le v^t \end{align} $$
である。

　よって
$$ \begin{align} \beta^2v^t\geq\omega(v_x)+\sqrt{\omega(v_x)^2+\beta^2||v_x||^2} \end{align} $$
となり、$v_x\ne0$のとき$v^t>0$である。また$v_x=0$のときは$v=v^t\partial_t$となり$\partial_t$が未来向きなので明らかに$v^t>0$である。

　$I^+(p)\supset I^+(q)$とすると、任意の$q^+\in I^+(q)$と$p$を結ぶ未来向きの時間的曲線が存在する。特に、$U$が生成する1パラメータ変換群を$\phi_t$とすると、任意の$\epsilon>0$に対して、$\phi_\epsilon(q)$と$p$を結ぶ未来向きの時間的曲線$\alpha:[0,1]\rightarrow M$が存在する。$U$は完備であるから$\phi_{-\epsilon}\circ\alpha$は定義される。この曲線のパラメータを反転させれば$q$から出て$\phi_{-\epsilon}(p)$へ至る過去向きの時間的曲線と見なせる。

　任意の$p^-\in I^-(p)$に対して、$p$と$p^-$を結ぶ時間的曲線$\gamma$を一つ取る。$p$の正規近傍を$V$とし$p'\in\gamma\cap V$とする。$V$上の因果的関係はMinkowski時空のそれと同じだから
$\epsilon$を必要なら十分小さく取れば$p'\in I^-(\phi_{-\epsilon}(p))$とできることが分かる。よってこのとき$p^-\in I^-(p')\subset I^-(q)$である。

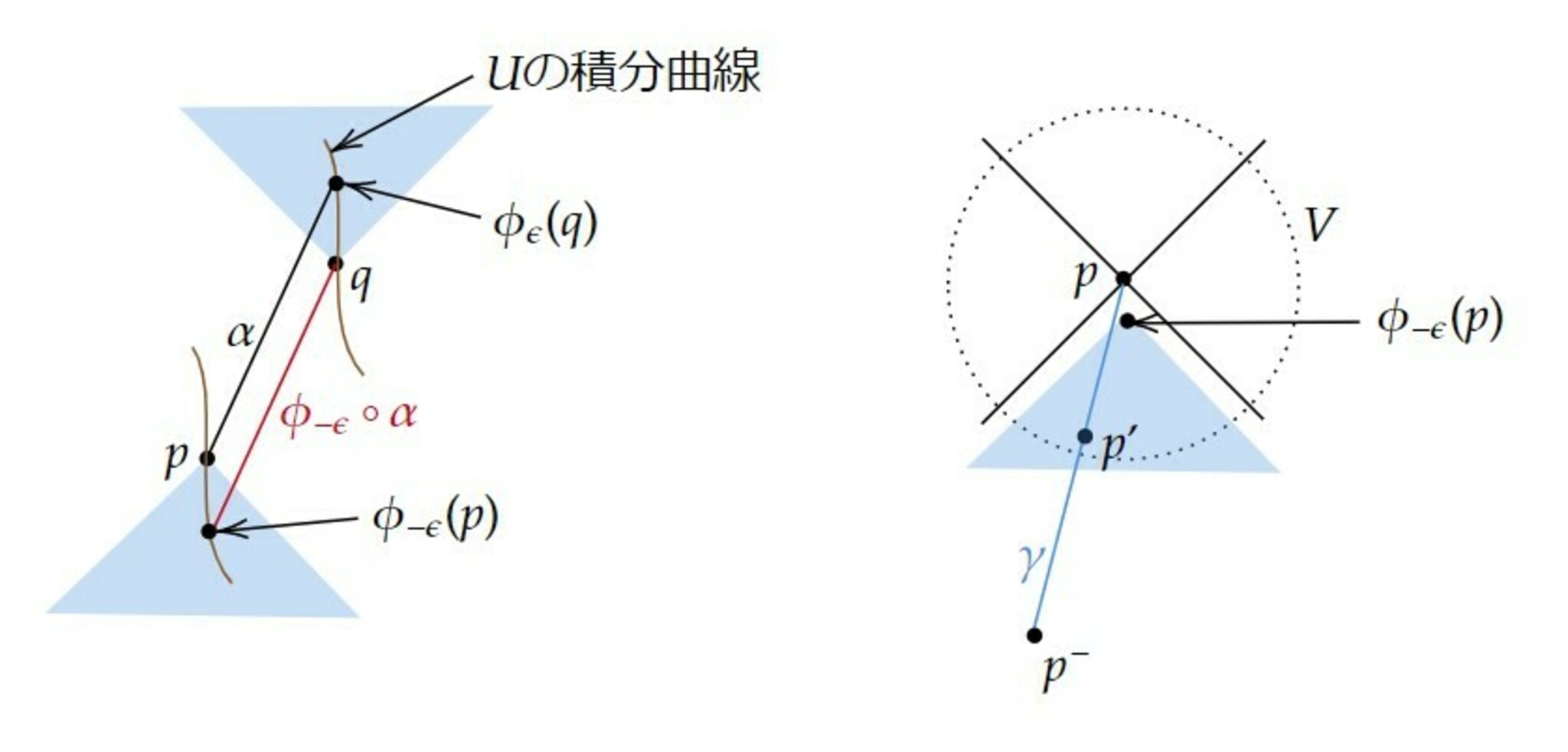証明の模式図

　もし$U$の各積分曲線とただ一度交わる空間的超曲面$S$が存在すれば、標準的定常時空となる。なぜなら$U$が生成するフローを$\Psi:\mathbb{R}\times M\rightarrow M$とすると、$\Phi_S:\mathbb{R}\times S\ni(t,p)\mapsto \Phi(t,p)\in M$は微分同相であり、$(\mathbb{R}\times S,\Phi_S^\ast g)$は明らかに標準的定常時空である。よってこのような$S$の存在を示せば良い。

　$U$の軌道空間を$Q$とすると、$M$は$Q$上の直線束となるから$M\simeq \mathbb{R}\times Q$と分解される。可微分時間関数を$t$とすると、${\rm grad}\ t$が時間的だから$S=t^{-1}(0)$は空間的超曲面である。$t$は時間関数であり、任意の時間曲線に沿って狭義単調増加するため、$S$と因果的曲線が交わるなら唯一点で交わる（この性質を持つ集合は順時的集合と呼ばれる）。よって$U$の各積分曲線と交わるならば唯一点である。従って$S\simeq Q$を示せば良い（全ての$U$の積分曲線と交わるかどうかまだ分からない）。

　分解$M\simeq \mathbb{R}\times Q$に関して第二成分への射影を$\pi:M\rightarrow Q$とする。$S$は順時的集合なので$\pi|_S$は単射である。またinvariance of domainより$\pi(S)$は開集合である。さらに$M$は連結であるから$Q$も連結である。従って$\pi(S)$が閉集合であることを示せば良い。

　$p\in M$の分解$M\simeq \mathbb{R}\times Q$に関する成分表示を$p=(t,x)_\ell$と書くことにする($\ell$はline bundleの$\ell$)。$S$の点列$\{z_n=(\hat t_n,\hat x_n)_\ell\}\in S$に対して、$\hat x_n\rightarrow \hat x_\infty\in Q$とする。

　$\hat x_\infty\notin\pi(S)$と仮定して矛盾を導く。もし$\hat t_n$が収束するなら$z_n$が極限を持ち$S$は閉集合だから$z_n\rightarrow z_\infty\in S$となり矛盾する。よって$\hat t_n$は発散する。$\hat t_n\rightarrow+\infty$と仮定してよい。

$\hat V$を$\hat x_\infty$を含む$Q$の開近傍とする。$\pi^{-1}(\hat V)$には空間的超曲面である切断が存在するから$\pi^{-1}(\hat V)$は標準的定常時空である。その切断を$V\subset \pi^{-1}(\hat V)$とし、$\pi^{-1}(\hat V)$の標準的定常時空への分解を$\pi^{-1}(\hat V)=\mathbb{R}\times V$とする。この分解に関する成分表示を$z_n=(t_n,x_n)_s$とする。

　関数$T:V\times V\rightarrow[0,\infty)$を
$$ T(x,y):=\inf\{t;\ (0,x)_s<<(t,y)_s\} $$
と定義すると、$T$は$V\times V$上で連続である(証明は少し長いのでAppendixに回す)。$T_W:=\inf_{x,y\in W} T(x,y)$と定義する。

十分大きい$n_0$に対して、$x_{n_0}\in W$とできる。$n>n_0$に対して、$T_W$の定義より$t_n\geq t_{n_0}+T_W,\ x_n\in W$だから$(t_n,x_n)_s\in I^+((t_{n_0},x_{n_0})_s)$である。よって$S$が順時的集合であることに矛盾する。

証明の模式図

　$M$の計量を$ g=-\beta dt^2+2\omega dt+g_V$とする（記号は定義2と同じ意味）。$\gamma:[0,1]\to V$を$V$上の$C^1$級曲線で$g_V(\dot\gamma,\dot\gamma)=1$を満たすものとする。$f\in C^1([0,1])$に対して、方程式
$$ -\beta f'^2+2f'\omega(\dot\gamma)+1=0 $$
は解を持つ。この方程式の正の解を$f$とすると、曲線$\tilde\gamma(u):=(f(u),\gamma(u))_s$は$(0,x)_s$と時間的曲線$R_y:=\{(u,y)_s;\ u\in\mathbb{R}\}$を結ぶ光的曲線である。従って、$J^+((0,x)_s)\cap R_y\ne\emptyset$である。

　$(T_0,y)_s\in \partial J^+((0,x)_s)=J^+((0,x)_s)-I^+((0,x)_s)$とする。$ T< T_0$に対して、$(T,y)_s\in J^+((0,x)_s)$となることはありえない。なぜならもしそうなったら、$(0,x)_s<(T,y)_s<<(T_0,y)_s$なので$(0,x)_s<<(T_0,y)_s$であるから、$(T_0,y)_s\in I^+((0,x)_s)$となり、矛盾する。よって$(T,y)_s\notin J^+((0,x)_s)$である。また$T>T_0$に対しても同様に$ (T,y)_s\in I^+((0,x)_s)$である。よって$T_0$は望みの性質を持つ。

　まず$y$に関する連続性を示す。$ \partial J^+((0,x)_s)=\{(T(x,y),y)_s;\ y\in V\}$である。点列$\{y_n\}\in V$で$y_n\to y$かつ$ T(x,y_n)\to T'\ne T(x,y)$となるものがあるとする。$ \partial J^+((0,x)_s)$は閉集合だから$ (T',y)_s\in\partial J^+((0,x)_s)$となる。$ T'\ne T(x,y)$だから、$ t\ne T'$で$ (t,y)_s\in\partial J^+((0,x)_s)$となる$ t$があることになり、存在性の証明と同様の矛盾が生じる。

　最期に$ x$に関する連続性を示す。点列$\{x_n\}\in V$を$ x_n\to x,\ T(x_n,y)\to T'\ne T(x,y)$を満たすものとする。
(i) $T'< T(x,y)$のとき
$ (T',y)_s\notin J^+((0,x)_s)$であり、$ J^+((0,x)_s)$は閉集合だから$ (T',y)_s$のコンパクトな近傍$K$があって$ K\cap J^+((0,x)_s)=\emptyset$とできる。$M$は標準的定常時空であり、定理7より因果的連続時空であるから、$I^\pm$は外側連続である。よって$ x$の適当な近傍$ U$があって、任意の$x'\in U$に対して、$ J^+((0,x')_s)\cap K=\emptyset$となる。これは$ x_n\to x$のとき$T(x_n,y)\to T$となることに矛盾する。
(ii) $T'> T(x,y)$のとき
$I^\pm$の内側連続性（常に成り立つ）から同様の議論が成り立つ。