ヤコビの楕円関数の諸性質
はじめに
この記事では今後の記事に向けてヤコビの楕円関数の基本的な性質について解説していきます。
定義
第一種不完全楕円積分
$$u=K(x,k)=\int^x_0\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}\quad(0\leq k\leq1,-1\leq x\leq1)$$
の逆関数を$x=\sn(u,k)$とおき、$-K\leq x\leq K\;(K=K(1,k))$において
$$\cn(u,k)=\sqrt{1-\sn^2(u,k)},\quad\dn(u,k)=\sqrt{1-k^2\sn^2(u,k)}$$
と定める。これらの関数$\sn,\cn,\dn$をヤコビの楕円関数という。
必要に応じて$k$を省略し$\sn u,\cn u,\dn u$とも書きます。
楕円積分に付随するパラメーター$k$を母数(modulus)といい、これに対して$k'=\sqrt{1-k^2}$と定められるパラメーターを補母数(complementary modulus)という。
また慣例として第一種完全楕円積分
$$K=K(1,k)=\int^1_0\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}$$
について$K(1,k')$を$K'$と表す。微分との混同を避けるため$dK/dk$は$\dot K$と書かれる。
$K(x,k)$は$-1\leq x\leq1$において単調増加であることから$\sn u$は$-K\leq u\leq K$において正常に定まります。また
$$\frac{dK}{dx}(0,k)=1\neq0$$
より(逆関数定理から)$\sn u$は$u=K(0,k)=0$の近傍で正則関数を定めることがわかります。
楕円積分の性質$K(0,k)=0, K(-x,k)=-K(x,k)$より
$$\sn0=0,\;\cn0=\dn0=1$$
であることや$\sn$は奇関数、$\cn,\dn$は偶関数であることがわかります。
$k=0$のとき
$$K(x,0)=\int^x_0\frac{dt}{\sqrt{1-t^2}}=\sin^{-1}x$$
なので
\begin{eqnarray}
\sn(x,0)&=&\sin x
\\\cn(x,0)&=&\cos x
\\\dn(x,0)&=&1
\end{eqnarray}
となります。
$k=1$のとき
$$K(x,1)=\int^x_0\frac{dt}{1-t^2}=\tanh^{-1}x$$
なので
\begin{eqnarray}
\sn(x,1)&=&\tanh x
\\\cn(x,1)&=&1/\cosh x=\operatorname{sech}x
\\\dn(x,1)&=&\operatorname{sech}x
\end{eqnarray}
となります。
微分方程式
\begin{eqnarray}
(\sn u)'&=&\cn u\dn u
\\(\cn u)'&=&-\sn u\dn u
\\(\dn u)'&=&-k^2\sn u\cn u
\end{eqnarray}
が成り立つ。
$\sn$の定義より
$$u=\int^{\sn u}_0\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}$$
が成り立つのでこの両辺を微分することで
$$1=\frac{(\sn u)'}{\sqrt{(1-\sn^2u)(1-k^2\sn^2u)}}=\frac{(\sn u)'}{\cn u\dn u}$$
つまり
$$(\sn u)'=\cn u\dn u$$
を得る。
あとは
\begin{eqnarray}
\cn^2u&=&1-\sn^2u
\\\dn^2u&=&1-k^2\sn^2u
\end{eqnarray}
を微分することでわかる。
$\sn u$の微分方程式は$(x,y)=(\sn u,(\sn u)')$とおくと
$$y^2=(1-x^2)(1-k^2x^2)$$
と表すことができます。これは同じ基本的な楕円関数である
ワイエルシュトラスの$\wp$関数
の満たす微分方程式
$$y^2=4x^3-g_2x-g_3\qquad((x,y)=(\wp,\wp'))$$
の類似のようなものとなっています。
$$(\sn u)''=-\sn u(1+k^2-2k^2\sn^2u)$$
が成り立つ。
上の結果より
\begin{eqnarray}
(\sn u)''&=&-\sn u\dn^2u-k^2\sn u\cn^2u
\\&=&-\sn u((1-k^2\sn^2 u)+k^2(1-\sn^2 u))
\\&=&-\sn u(1+k^2-2k^2\sn^2u)
\end{eqnarray}
と計算できる。
加法定理
\begin{eqnarray*}
\sn(u+v)&=&\frac{\sn u\cn v\dn v+\sn v\cn u\dn u}{1-k^2\sn^2u\sn^2v}
\\\cn(u+v)&=&\frac{\cn u\cn v-\sn u\dn u\sn v\dn v}{1-k^2\sn^2u\sn^2v}
\\\dn(u+v)&=&\frac{\dn u\dn v-k^2\sn u\cn u\sn v\cn v}{1-k^2\sn^2u\sn^2v}
\end{eqnarray*}
が成り立つ。
ある程度発見的に説明しておくと$k=0,1$の場合を考えたとき
\begin{eqnarray}
\sin(x+y)&=&\sin x\cos y+\sin y\cos x
\\&=&\sin x(\sin y)'+\sin y(\sin x)'
\\\tanh(x+y)&=&\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}
\\&=&\frac{\tanh x(1-\tanh^2y)+\tanh y(1-\tanh^2x)}{1-\tanh^2x\tanh^2y}
\\&=&\frac{\tanh x(\tanh y)'+\tanh y(\tanh x)'}{1-\tanh^2x\tanh^2y}
\end{eqnarray}
という加法定理があるので、これを両立するようなものを考えると
$$\sn(u+v)=\frac{\sn u(\sn v)'+\sn v(\sn u)'}{1-k^2\sn^2u\sn^2v}$$
という式が浮かび上がってきます。
簡単のため$x=\sn u,\;y=\sn v$とおき、$u$による微分を$dx/du=\dot x$のように表す。
このとき$u+v=(一定)$において
$$\frac{\sn u\cn v\dn v+\sn v\cn u\dn u}{1-k^2\sn^2u\sn^2v}
=\frac{-x\dot y+y\dot x}{1-k^2x^2y^2}$$
が不変であること、つまりその$u$による微分が$0$となることを示す。また、これを対数微分すると
$$\frac{y\ddot x-x\ddot y}{y\dot x-x\dot y}
+\frac{2k^2xy}{1-k^2x^2y^2}\l(y\dot x+y\dot x\r)$$
となるのでこれが$0$であるためには
$$\frac{y\ddot x-x\ddot y}{(y\dot x)^2-(x\dot y)^2}=-\frac{2k^2xy}{1-k^2x^2y^2}$$
を示せばよい。
そのことは定理1より
\begin{eqnarray}
(\dot x)^2&=&(1-x^2)(1-k^2x^2)
\\(\dot y)^2&=&(1-y^2)(1-k^2y^2)
\end{eqnarray}
であったことと定理1系より
\begin{eqnarray}
\ddot x&=&-x(1+k^2-2k^2x^2)
\\\ddot y&=&-y(1+k^2-2k^2y^2)
\end{eqnarray}
であったことから
\begin{eqnarray}
y^2(\dot x)^2-x^2(\dot y)^2&=&(1-k^2x^2y^2)(y^2-x^2)
\\y\ddot x-x\ddot y&=&-2k^2xy(y^2-x^2)
\end{eqnarray}
と確かめられる。
よって
$$\frac{\sn u\cn v\dn v+\sn v\cn u\dn u}{1-k^2\sn^2u\sn^2v}$$
は$u+v=(一定)$において不変であり、$(u,v)\mapsto(u+v,0)$とするとこれが$\sn(u+v)$に一致することがわかる。
$\cn,\dn$の加法定理については
$$\cn u=\sqrt{1-\sn^2u},\;\dn u=\sqrt{1-k^2\sn^2u}$$
を頑張って変形することでわかる。
あるいは$(x,y)=(\cn u,\cn v),(\dn u,\dn v)$とおいて$u+v=(一定)$における
\begin{eqnarray}
\frac{\cn u\cn v-\sn u\dn u\sn v\dn v}{1-k^2\sn^2u\sn^2v}
&=&\frac{xy+\dot x\dot y}{1-k^2(1-x^2)(1-y^2)}
\\\frac{\dn u\dn v-k^2\sn u\cn u\sn v\cn v}{1-k^2\sn^2u\sn^2v}
&=&\frac{k^2xy+\dot x\dot y}{k^2-(1-x^2)(1-y^2)}
\end{eqnarray}
の不変性を示すことでも確かめられるが、あまりおすすめはしない。
実関数への拡張
ヤコビの楕円関数は$-K\leq u\leq K$において定義された関数でしたが、加法定理によって実数上の関数に延長することができます。
\begin{eqnarray*}
\sn(u+K)&=&\frac{\cn u}{\dn u}&=&&&\sn(K-u)
\\\cn(u+K)&=&-k'\frac{\sn u}{\dn u}&=&&-&\cn(K-u)
\\\dn(u+K)&=&k'\frac1{\dn u}&=&&&\dn(K-u)
\end{eqnarray*}
および
\begin{eqnarray*}
\sn(u+2K)&=&-\sn u
\\\cn(u+2K)&=&-\cn u
\\\dn(u+2K)&=&\dn u
\end{eqnarray*}
が成り立つ。
加法定理において$v=K$としたとき
$$\sn K=1,\;\cn K=0,\;\dn K=\sqrt{1-k^2}=k'$$
および
$$1-k^2\sn^2u=\dn^2u$$
に注意すると
\begin{eqnarray*}
\sn(u+K)&=&\frac{\cn u}{\dn u}
\\\cn(u+K)&=&-k'\frac{\sn u}{\dn u}
\\\dn(u+K)&=&k'\frac1{\dn u}
\end{eqnarray*}
がわかり、この式において$u\mapsto-u$とすると$\sn$は奇関数、$\cn,\dn$は偶関数であることから
\begin{eqnarray*}
\sn(u+K)&=&&&\sn(K-u)
\\\cn(u+K)&=&&-&\cn(K-u)
\\\dn(u+K)&=&&&\dn(K-u)
\end{eqnarray*}
がわかる。これに$u=K$を代入すると
$$\sn2K=0,\;\cn2K=-1,\;\dn2K=1$$
がわかるので、再び加法定理において$v=2K$とすることで
\begin{eqnarray*}
\sn(u+2K)&=&-\sn u
\\\cn(u+2K)&=&-\cn u
\\\dn(u+2K)&=&\dn u
\end{eqnarray*}
を得る。
これらの式から次のようにグラフを書くことができます。
| $u$ | $-2K$ | $-K$ | $0$ | $K$ | $2K$ |
|---|---|---|---|---|---|
| $\sn u$ | $0$ | $-1$ | $0$ | $1$ | $0$ |
| $\cn u$ | $-1$ | $0$ | $1$ | $0$ | $-1$ |
| $\dn u$ | $1$ | $k'$ | $1$ | $k'$ | $1$ |
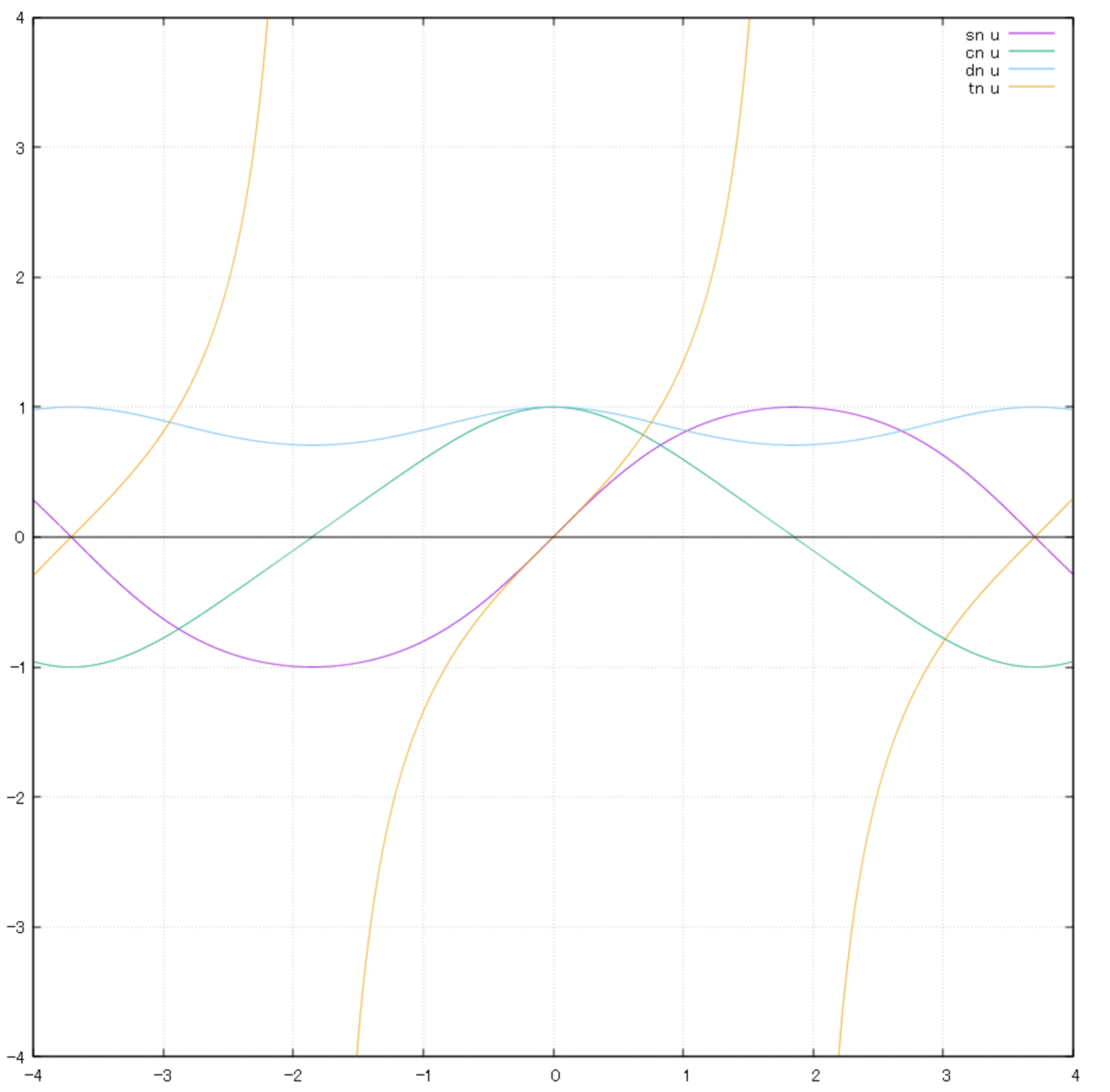k=1/√2のときの各関数のグラフ(K=1.854074...)
複素関数への拡張
\begin{eqnarray}
\sn(iv,k)&=&i\frac{\sn(v,k')}{\cn(v,k')}
\\\cn(iv,k)&=&\frac1{\cn(v,k')}
\\\dn(iv,k)&=&\frac{\dn(v,k')}{\cn(v,k')}
\end{eqnarray}
が成り立つ。
$$\tn u=\frac{\sn u}{\cn u}$$
という関数を考えると
\begin{eqnarray}
1+\tn^2u&=&\frac1{\cn^2u}
\\1+k'^2\tn^2u&=&\frac{(1-\sn^2u)+(1-k^2)\sn^2u}{\cn^2u}
=\frac{\dn^2u}{\cn^2u}
\end{eqnarray}
から
$$(\tn u)'=\frac{\dn u}{\cn^2u}
=\sqrt{(1+\tn^2u)(1+k'^2\tn^2u)}$$
が成り立つので、
$$\int^{\tn(v,k')}_0\frac{dt}{\sqrt{(1+t^2)(1+k^2t^2)}}=v$$
がわかる。また$it=s$とおくと
$$\int^{i\tn(v,k')}_0\frac{ds}{\sqrt{(1-s^2)(1-k^2s^2)}}=iv
=\int^{\sn(iv,k)}_0\frac{ds}{\sqrt{(1-t^2)(1-k^2t^2)}}$$
が成り立つので、逆関数の一意性より
$$\sn(iv,k)=i\tn(v,k')=i\frac{\sn(v,k')}{\cn(v,k')}$$
を得る。
あとは
\begin{eqnarray}
\cn(iv,k)&=&\sqrt{1-\sn^2(iv,k)}&=&\sqrt{1+\tn^2(v,k')}
\\\dn(iv,k)&=&\sqrt{1-k^2\sn^2(iv,k)}&=&\sqrt{1+k^2\tn^2(v,k')}
\end{eqnarray}
よりわかる。
いま
\begin{eqnarray}
&&\cn^2(v,k')+k^2\sn^2(u,k)\sn^2(v,k')
\\&=&1-(1-k^2\sn^2(u,k))\sn^2(v,k')
\\&=&1-\dn^2(u,k)\sn^2(v,k')
\end{eqnarray}
に注意すると、定理3と加法定理よりヤコビの楕円関数は次のように複素関数に拡張されることがわかります。
\begin{eqnarray}
\sn(u+iv,k)
&=&\frac{\sn(u,k)\dn(v,k')+i\cn(u,k)\dn(u,k)\sn(v,k')\cn(v,k')}{1-\dn^2(u,k)\sn^2(v,k')}
\\\cn(u+iv,k)
&=&\frac{\cn(u,k)\cn(v,k')-i\sn(u,k)\dn(u,k)\sn(v,k')\dn(v,k')}{1-\dn^2(u,k)\sn^2(v,k')}
\\\dn(u+iv,k)
&=&\frac{\dn(u,k)\cn(v,k')\dn(v,k')-ik^2\sn(u,k)\cn(u,k)\sn(v,k')}{1-\dn^2(u,k)\sn^2(v,k')}
\end{eqnarray}
が成り立つ。
この式と定理2系の式
\begin{eqnarray*}
\sn(u+2K)&=&-\sn u
\\\cn(u+2K)&=&-\cn u
\\\dn(u+2K)&=&\dn u
\end{eqnarray*}
から$\sn$は$4K$と$2iK'$を、$\cn$は$4K$と$2K+2iK'$を、$\dn$は$2K$と$4iK'$を基本周期に持つ二重周期関数となります。
$K(1,0)=\infty$より$k=0,1$のときは一方の周期性を失うことなります。その結果が三角関数$\sin$や双曲線三角関数$\tanh$であったわけです。
\begin{eqnarray} \sn(u+iK')&=&\frac1{k\sn u} \\\cn(u+iK')&=&-i\frac{\dn u}{k\sn u} \\\dn(u+iK')&=&-i\frac{\cn u}{\sn u} \end{eqnarray}
$\sn(K',k')=1,\;\cn(K',k')=,\;\dn(K',k')=k$
に注意するとわかる。
零点と極
$\sn u$は
$$u=2mK+2niK'\quad(m,n\in\Z)$$
を一位の零点に持ち(導関数の値は$(-1)^m$)、
$$u=2mK+(2n+1)iK'\quad(m,n\in\Z)$$
を一位の極に持つ(留数の値は$(-1)^m/k$)。
$u$が実数のときの$\sn,\cn,\dn$の挙動
| $u$ | $-2K$ | $-K$ | $0$ | $K$ | $2K$ |
|---|---|---|---|---|---|
| $\sn u$ | $0$ | $-1$ | $0$ | $1$ | $0$ |
| $\cn u$ | $-1$ | $0$ | $1$ | $0$ | $-1$ |
| $\dn u$ | $1$ | $k'$ | $1$ | $k'$ | $1$ |
および
$$\sn(u+2mK+2miK')=(-1)^m\sn u\quad(m,n\in\Z)$$
に注意して領域$0\leq u<2K,\;0\leq v<2K'$における$\sn(u+iv,k)$の零点と極を考える。
$\sn(u+iv,k)$が極を取るとき
$$1-\dn^2(u,k)\sn^2(v,k')=0$$
が成り立つので、上の表からそのような$u,v$は
$$u+iv=iK'$$
に限ることがわかる。また定理4から
$$\sn(u+iK,k)=\frac1{k\sn(u,k)}$$
であったのでこれは一位の極になっていることがわかる。
またこの公式から
$u$が零点$\iff u\pm iK'$が極
となることがわかるので領域内の零点は
$u+iv=0$
のみであることがわかる。
同様にして以下のことがわかります。
$\cn u$は
$u=(2m+1)K+2niK'\quad(m,n\in\Z)$
を一位の零点に
$u=2mK+(2n+1)iK'\quad(m,n\in\Z)$
を一位の極に持つ。
$\dn u$は
$u=(2m+1)K+(2n+1)iK'\quad(m,n\in\Z)$
を一位の零点に
$u=2mK+(2n+1)iK'\quad(m,n\in\Z)$
を一位の極に持つ。
おまけ：半数公式
\begin{eqnarray} \sn\frac u2&=&\sqrt{\frac{1-\cn u}{1+\dn u}} \\\cn\frac u2&=&\sqrt{\frac{\dn u+\cn u}{1+\dn u}} \\\dn\frac u2&=&\sqrt{\frac{k'^2+\dn u+k^2\cn u}{1+\dn u}} \end{eqnarray}
加法定理より$x=\sn u$とおくと倍数公式は
\begin{eqnarray}
\cn2u&=&\frac{\cn^2u-\sn^2u\dn^2u}{1-k^2\sn^4u}
=\frac{1-2x^2+k^2x^2}{1-k^2x^4}
\\\dn2u&=&\frac{\dn^2u-k^2\sn^2u\cn^2u}{1-k^2\sn^4u}
=\frac{1-2k^2x^2+k^2x^4}{1-k^2x^4}
\end{eqnarray}
となるので、
$$\frac{1-\cn2u}{1+\dn2u}=\frac{2x^2-2k^2x^4}{2-2k^2x^2}=x^2$$
を得る。あとは
$$\cn u=\sqrt{1-\sn^2u},\;\dn u=\sqrt{1-k^2\sn^2u}$$
からわかる。
半数公式に$u=K$を代入することで以下の特殊値がわかります。
\begin{eqnarray}
\sn\frac K2&=&\frac1{\sqrt{1+k'}}
\\\cn\frac K2&=&\sqrt{\frac{k'}{1+k'}}
\\\dn\frac K2&=&\sqrt{k'}
\end{eqnarray}
が成り立つ。特に
$$\sn\frac{iK'}2=\frac i{\sqrt k},\quad\sn\l(K+\frac{iK'}2\r)=\frac1{\sqrt k}$$
が成り立つ。
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
