文献あり

Bellの不等式(2/2): 量子計算機によるBellの不等式の破れの検証

416

★本記事は Bellの不等式(1/2): "同担拒否モデル"によるBellの不等式の導出の続きです。

量子計算機によるBellの不等式の破れの検証

まず前回の記事のまとめを記しておきます：

前回の記事では、Bellの不等式
$\begin{array}{r} P (a +; b +) \leq P (a +; c +) + P (c +; b +) \end{array}$
を、同担拒否の2人組への推しに関するアンケート結果から構成した。これはJJ.Sakuraiの教科書(Ref.[1])に記載されている形のBellの不等式である。次に、対応する量子力学的なBellの不等式を、3つの方向 $\hat{a}, \hat{b}, \hat{c}$ に対するスピンの測定により構成した。その結果
$\begin{array}{r} P (a +; b +) = \frac{1}{2} \sin^{2} θ, P (a +; c +) = P (c +; b +) = \frac{1}{2} \sin^{2} (\frac{θ}{2}) \end{array}$
を得た。よって上記のBellの不等式は量子論において
$\begin{array}{r} \frac{1}{2} \sin^{2} θ \leq \sin^{2} (\frac{θ}{2}) \end{array}$
となる。この式は $0 \leq θ < π / 2$ で破れる。

前回の記事の準備のもと、本記事では、実際に量子計算を実行し、上記のBellの不等式の破れを実機で確認します。

量子計算にはIBM Quantum Lab (Refs.[2][3])を用いました。Labでは、QiskitというオープンソースのPythonライブラリ(Ref.[4])を用い、量子計算機システムIBM Quantum Oneを使うことができます。Qiskitには大変丁寧なガイド・チュートリアルが存在します(Ref.[5])。この中の"Local Reality and the CHSH Inequality"というノートブックに、「CHSH不等式」というタイプのBellの不等式の破れの確認用コードがありますが、本記事ではこれと違った形の、上述したJJ.Sakuraiの教科書に記載のあるBellの不等式を確認してみます。

本記事の作成にあたり、IBM Quantum Canary Processor（Ref.[6]参照のこと）のひとつであるibmq_belemおよびibmq_quitoを使用しました。

量子計算機によるBellの不等式の破れの確認

まず今回使った量子回路の説明をします。次に量子計算の古典計算機によるシミュレーション結果を載せ、そのあと実際の量子計算の結果を示します。以下では前回記事における記法を使ってますので、適宜ご参照ください。

量子回路の説明

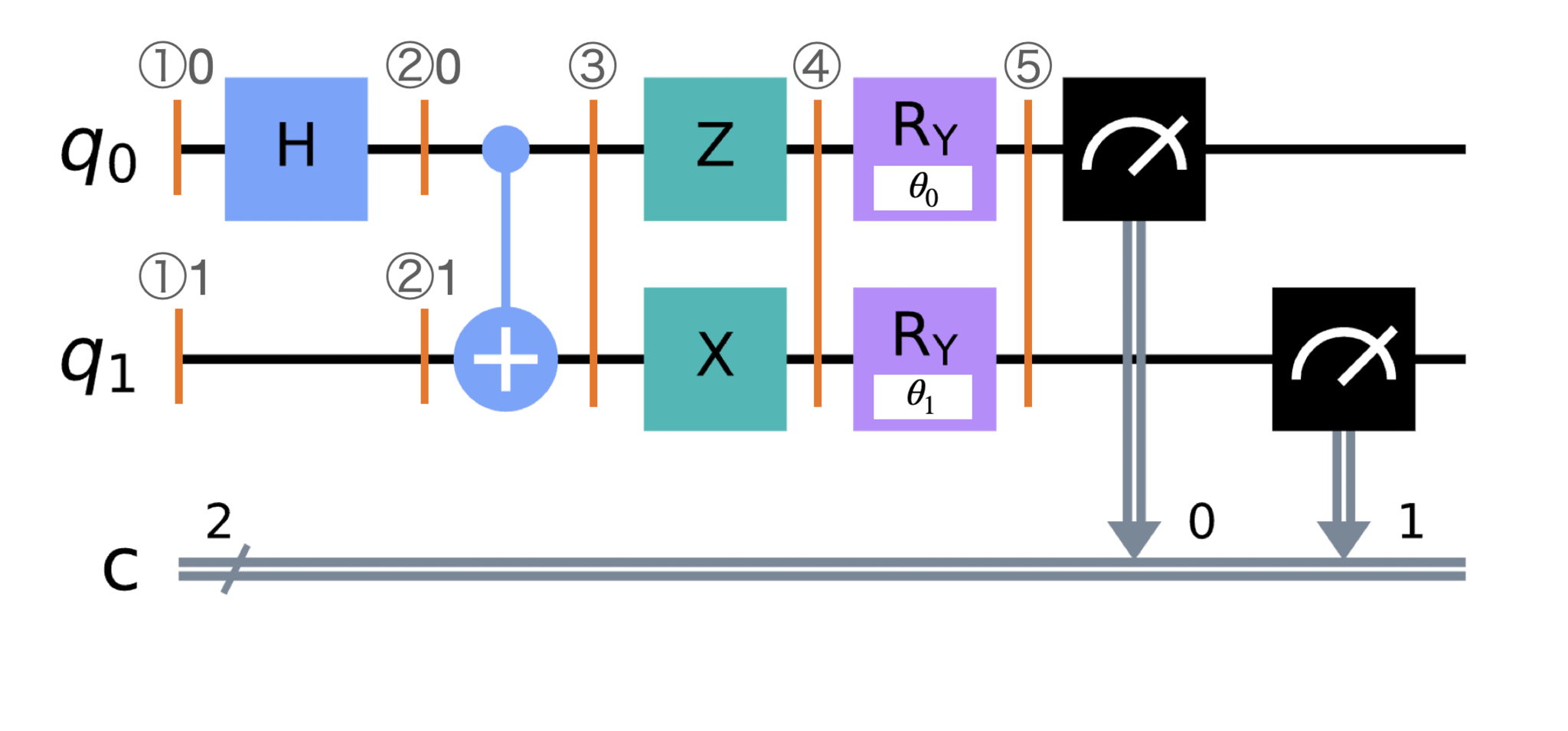
今回使った量子計算回路。!FORMULA[5][35784700][0]はy軸まわりの回転を表し、そこに示されている数字は回転角です。本図では特別な回転角が示されていますが、これは実際にはいくつか変化させて計算します。今回使った量子計算回路。 $R_{y}$ はy軸まわりの回転を表し、そこに示されている数字は回転角です。本図では特別な回転角が示されていますが、これは実際にはいくつか変化させて計算します。

図1は今回使った量子計算の回路です。図の各部分の説明は以下です：

量子ビットと古典ビット
上の2本の線が量子ビット(qubit)です。今回は2 qubit（ $q_{0}, q_{1}$ ）の計算を行います。
cと書いてある下の2重線は、古典的なビット(bit)です。2と書いてあるのは2bit用意してあることを意味します。これはqubitを計測して書き込むためのbitであり、量子計算には基本的に関係しません。よって上2本の線のみに注目すればよいです。
初期状態
初期状態を $q_{0}, q_{1}$ ともに $| 0 ⟩$ （z方向のスピンのプラス固有値の固有状態）にセットします。
スピン演算子
x,y,z方向のスピン演算子は、前回の記事の $S_{x}, S_{y}, S_{z}$ から $ℏ$ を除いたものとします:
$\begin{aligned} σ_{x} = (\begin{array}{c} 0 & 1 \\ 1 & 0 \end{array}), σ_{x} = (\begin{array}{c} 0 & - i \\ i & 0 \end{array}), σ_{x} = (\begin{array}{c} 1 & 0 \\ 0 & - 1 \end{array}) \\ S_{x} = σ_{x} / 2, S_{y} = σ_{y} / 2, S_{z} = σ_{z} / 2 \end{aligned}$
$S_{x}$ の $+ 1 / 2$ の固有値の固有状態を $| + ⟩$ 、 $- 1 / 2$ の固有値の固有状態を $| - ⟩$ と呼びます。このとき
$\begin{aligned} | + ⟩ & = \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩) \leftrightarrow \frac{1}{\sqrt{2}} (\begin{array}{c} 1 \\ 1 \end{array}), \\ | - ⟩ & = \frac{1}{\sqrt{2}} (| 0 ⟩ - | 1 ⟩) \leftrightarrow \frac{1}{\sqrt{2}} (\begin{array}{c} 1 \\ - 1 \end{array}) \end{aligned}$
です。（ちなみに以下では出てきませんが、 $S_{y}$ の固有状態を $| ↺ ⟩, | ↻ ⟩$ と書きます）
H: Hadamardゲート
HはHadamardゲートと呼ばれます。これは1qubitに対する操作で、
$\begin{aligned} H | 0 ⟩ & = | + ⟩, \\ H | 1 ⟩ & = | - ⟩, \end{aligned}$
のように基底を変換するunitary演算子です。
Controlled NOT (CNOT)ゲート
$q_{0}$ と $q_{1}$ をつなぐ青い線の端に青小丸と十字の入った大きい丸がついているのは、Controlled NOT (CNOT) ゲートです。これは、青小丸がついてる方のqubit(制御qubit)が $| 1 ⟩$ のとき、十字つきの丸がついているqubitを反転します。そうでないときは何もしません。すなわち、制御qubitにcをつけると
$\begin{aligned} | 1 ⟩_{c} | 0 ⟩ \to | 1 ⟩_{c} | 1 ⟩, \\ | 1 ⟩_{c} | 1 ⟩ \to | 1 ⟩_{c} | 0 ⟩, \\ | 0 ⟩_{c} | 0 ⟩ と | 0 ⟩_{c} | 1 ⟩ は不変 \end{aligned}$
という変換です。
Z: Zゲート
Zは1 qubitに対するゲートで $σ_{z}$ です。これは
$\begin{aligned} | 0 ⟩ & \to | 0 ⟩, \\ | 1 ⟩ & \to - | 1 ⟩, \end{aligned}$
という変換です。よって $| i ⟩ (i = 0, 1)$ を $(- 1)^{i} | i ⟩$ に変換します。このように状態のラベルに対応するphase（位相）を返すことを"phase kickback"と言います。
X: NOTゲート
Xは1 qubitに対するゲートでNOTゲートです。これは
$\begin{aligned} | 0 ⟩ & \to | 1 ⟩, \\ | 1 ⟩ & \to | 0 ⟩, \end{aligned}$
という変換です。
y軸まわりの回転
$R_{y}$ は、qubitをy軸のまわりに回転させる演算です。
具体的には
$\begin{array}{r} R_{y} (θ) = \exp (- \frac{i θ}{2} σ_{y}) = (\begin{array}{c} \cos \frac{θ}{2} & - \sin \frac{θ}{2} \\ \sin \frac{θ}{2} & \cos \frac{θ}{2} \end{array}) \end{array}$
です。図1の $R_{y}$ の下に示されている数字が回転角です。図では特別な値が代入されていますが、実際には様々に変化させて計算を行います。
測定
回路の右端には、計測器のような記号があります。これはそのとおり観測をする部分です。観測は $| 0 ⟩, | 1 ⟩$ の基底で行われます。qubit $q_{0}, q_{1}$ の観測結果（ $| 0 ⟩$ なら0、 $| 1 ⟩$ なら1）をclassical bit 1,2に書き込みます。

次に、初期の入力、および各ゲートを通過した後の状態を以下に記します：

初期状態および各ゲートの出力の説明用の図

①0: $| 0 ⟩$ , ①1: $| 0 ⟩$
②0: $| + ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩)$ , ②1: $| 0 ⟩$
③: $\frac{1}{\sqrt{2}} (| 0 ⟩ | 0 ⟩ + | 1 ⟩ | 1 ⟩)$ ...CNOTゲートによりエンタングルした状態
④: $\frac{1}{\sqrt{2}} (| 0 ⟩ | 1 ⟩ - | 1 ⟩ | 0 ⟩)$ ...全スピン0の2粒子状態
⑤: $\frac{1}{\sqrt{2}} (R_{y} (θ_{0}) | 0 ⟩ R_{y} (θ_{1}) | 1 ⟩ - R_{y} (θ_{0}) | 1 ⟩ R_{y} (θ_{1}) | 0 ⟩)$

上記は量子ゲートの性質よりすぐに導けます。

ここで重要なのは、③のCNOTゲートの出力状態です。このゲートを通った後の状態は、それぞれのqubitの状態を指定するのではなく、 $q_{0}, q_{1}$ 全体で状態を指定する必要があります。これが2粒子がエンタングルした状態であり、両者は相関を持ちます。

この回路を用いて、以下の実験を行いました：

④における全スピン0の状態： $\frac{1}{\sqrt{2}} (| 0 ⟩ | 1 ⟩ - | 1 ⟩ | 0 ⟩)$ に対して

「 $q_{0}$ に対し $\hat{a}$ 方向、 $q_{1}$ に対し $\hat{b}$ 方向の測定を行う」=「 $q_{0}$ の $R_{y}$ の角度を $0$ 、 $q_{1}$ の $R_{y}$ の角度を $2 θ$ として観測する」 $\to P (a +, b +)$ を得る
「 $q_{0}$ に対し $\hat{a}$ 方向、 $q_{1}$ に対し $\hat{c}$ 方向に測定を行う」=「 $q_{0}$ の $R_{y}$ の角度を $0$ 、 $q_{1}$ の $R_{y}$ の角度を $θ$ として観測する」 $\to P (a +, c +)$ を得る
「 $q_{0}$ に対し $\hat{c}$ 方向、 $q_{1}$ に対し $\hat{b}$ 方向に測定を行う」= 「 $q_{0}$ の $R_{y}$ の角度を $θ$ 、 $q_{1}$ の $R_{y}$ の角度を $2 θ$ として観測する」 $\to P (c +, b +)$ を得る

ここで $\hat{a}, \hat{b}, \hat{c}$ は $x$ - $z$ 平面上図3のように設定しています：

!FORMULA[82][-148884171][0]の方向。どれもx-z平面上に存在している。 $\hat{a}, \hat{b}, \hat{c}$ の方向。どれもx-z平面上に存在している。

この実験に関する理論的な計算に関しては、前回の記事をご参照ください。

計算結果

最初に、量子論におけるBellの不等式を再度記しておきます：
$\begin{array}{r} (1) & P (a +; b +) \leq P (a +; c +) + P (c +; b +) \leftrightarrow \frac{1}{2} \sin^{2} θ \leq \sin^{2} (\frac{θ}{2}) \end{array}$
これは $0 < θ < π / 2$ において破れます。

古典計算機におけるシミュレーション

図4は前章の実験を古典計算機においてシミュレーションした結果です。横軸はEq.(1)の角度 $θ$ （unit: radian）、赤丸が $P (a +, b +)$ 、青バツが $P (a +, c +) + P (c +, b +)$ です。統計は5000で計算しました。

古典計算機によるBellの不等式の破れのシミュレーション。横軸は $θ$ (rad)。Nshot(統計数)は5000。

これを見ると、たしかにEq.(1)の左辺と右辺を良い精度で再現していることがわかります。すなわち赤丸は $\sin^{2} (θ) / 2$ 、青バツは $\sin^{2} (θ / 2)$ をよく再現しています。そして $θ = 0$ から $π / 2$ においてEq.(1)が破れています。この準備により、統計は5000あれば十分Bellの不等式の破れを観測できることがわかります。

量子計算機における実際の検証

図5は量子計算機によるBellの不等式の破れの測定結果です。横軸・縦軸は図4と同じです。統計も同じ5000で計算しました。

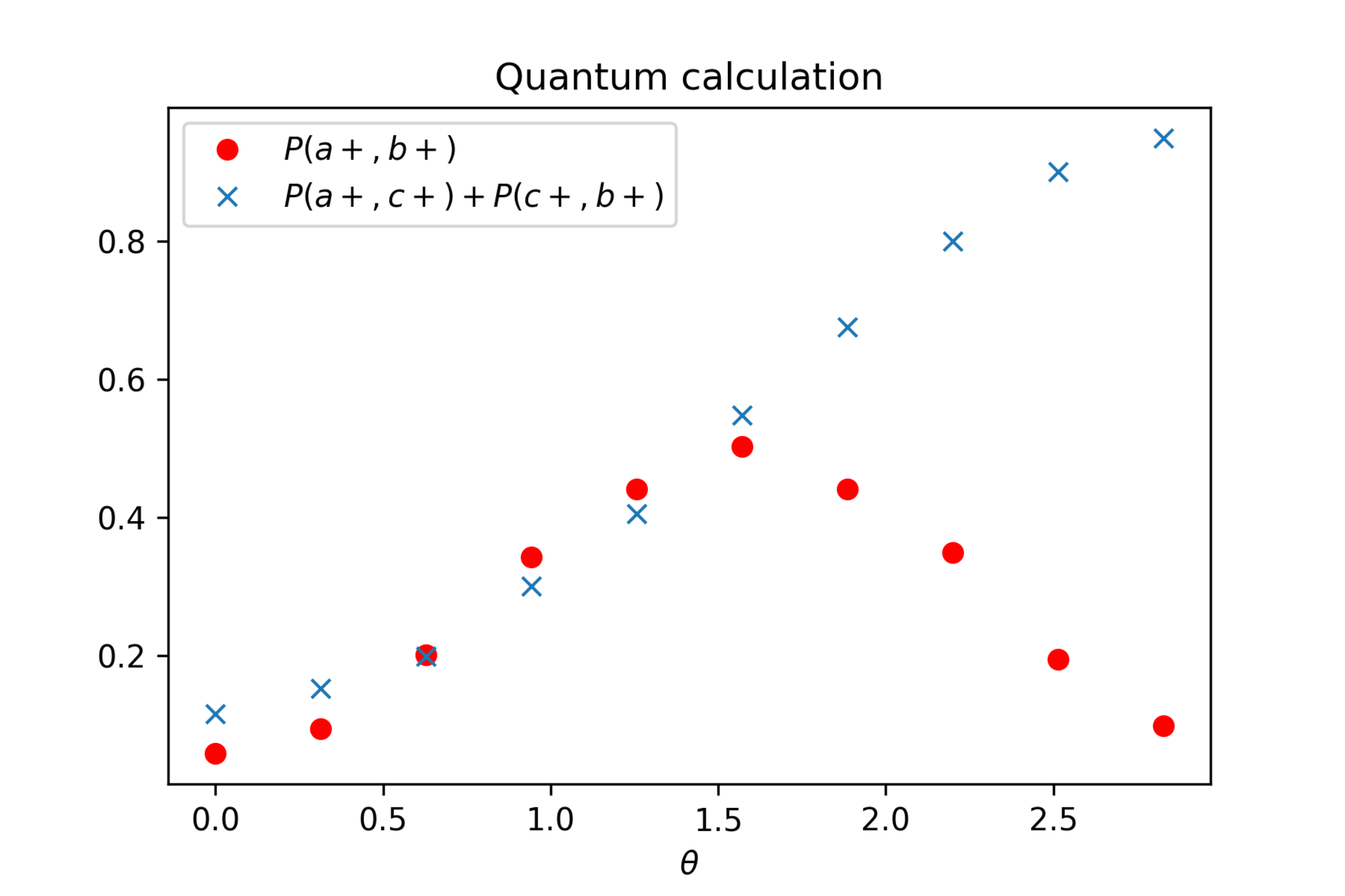量子計算機における検証。図4と同じnotationを用いている。Nshot=5000。

これを見ると、たしかに $θ = 0.6 - 1.5$ 付近でBellの不等式が破れていることが確認できます（エラーバーをつけていませんがご容赦ください）。ただし、 $θ$ が小さい2点で、大小関係が古典計算機の場合と入れ替わっています。この傾向は何回か計算をやり直しても同じなので、統計誤差ではなく、量子ゲートの操作や測定時に生じる系統的な誤差なのだと思います。Qiskitのdocumentでも、特に測定において誤差が生じる旨が記されています。

それでも十分にBellの不等式の破れを確認できます。私の想像よりはるかに綺麗なグラフが得られました。ちなみに今回の計算にかかる時間は、計算機の待ち時間を除くと、1つの角度に関して10から30秒程度で終わります。つまり"すぐ"終わると言っていいです。

どの計算機resourceが自分に使用可能であり、各resourceにどのくらいpendingのジョブ（ジョブ待ち）があり、また投入したジョブの状態がどうなっているか等は全てIBM Quantum Labから確認することができます。これらを確認しながら適切に計算を行いましょう。

まとめ

今回はIBM Quantum Labにおいて量子計算を行うことにより、量子論においてBellの不等式が破れることを実際に確かめました。この事実は、量子論は確率に支配される理論ではあるが、古典統計系とは本質的に異なることを示しています。

このような実験が手軽に行えるようになったのは本当に素晴らしいと思います。すごい時代になったなぁと感じます。

おしまい。 $_{◼}$

Acknowledgment

We acknowledge the use of IBM Quantum services for this web article. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.