【良問オブザイヤー2022】エントリー問題

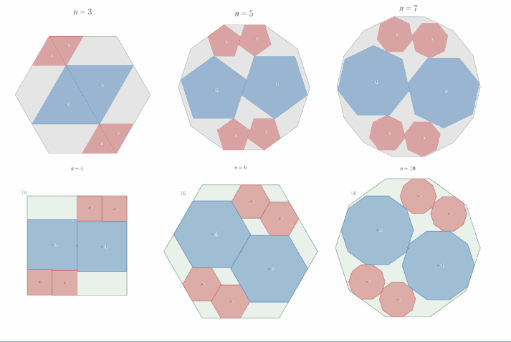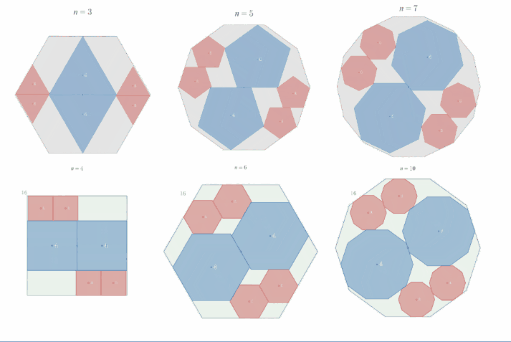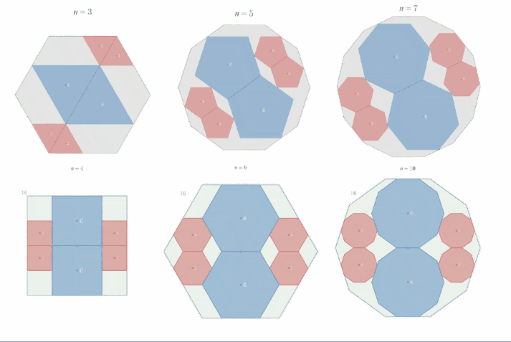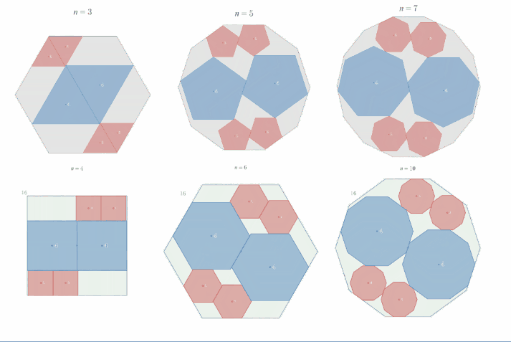
$n$ を $3$ 以上の奇数又は $4$ 又は $6$ とする。

$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $2$ の正 $2n$ 角形 $A$ を配置する。

$y$ 軸上に中心をもち、中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。

このとき、$B_1$又は$B_2$と外接し、かつ　$x$ 軸とも接するように、「中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接することを示せ。

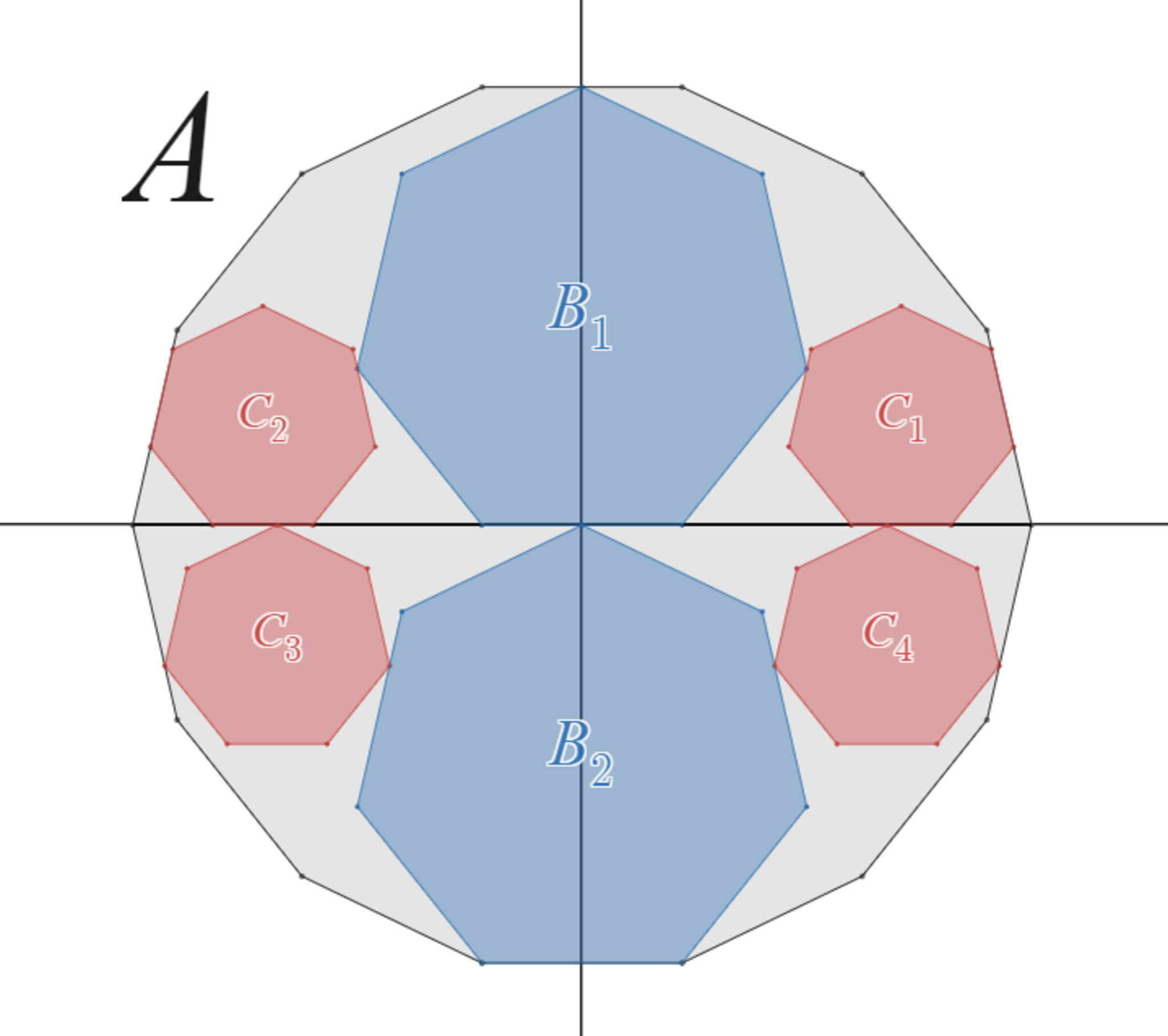相似比2:1の正"奇数"角形内接の定理
※　$C$ の場所は $4$ 箇所あります。区別するため、象限にあわせて $C_1$ ～ $C_4$ と添え字をつけています。

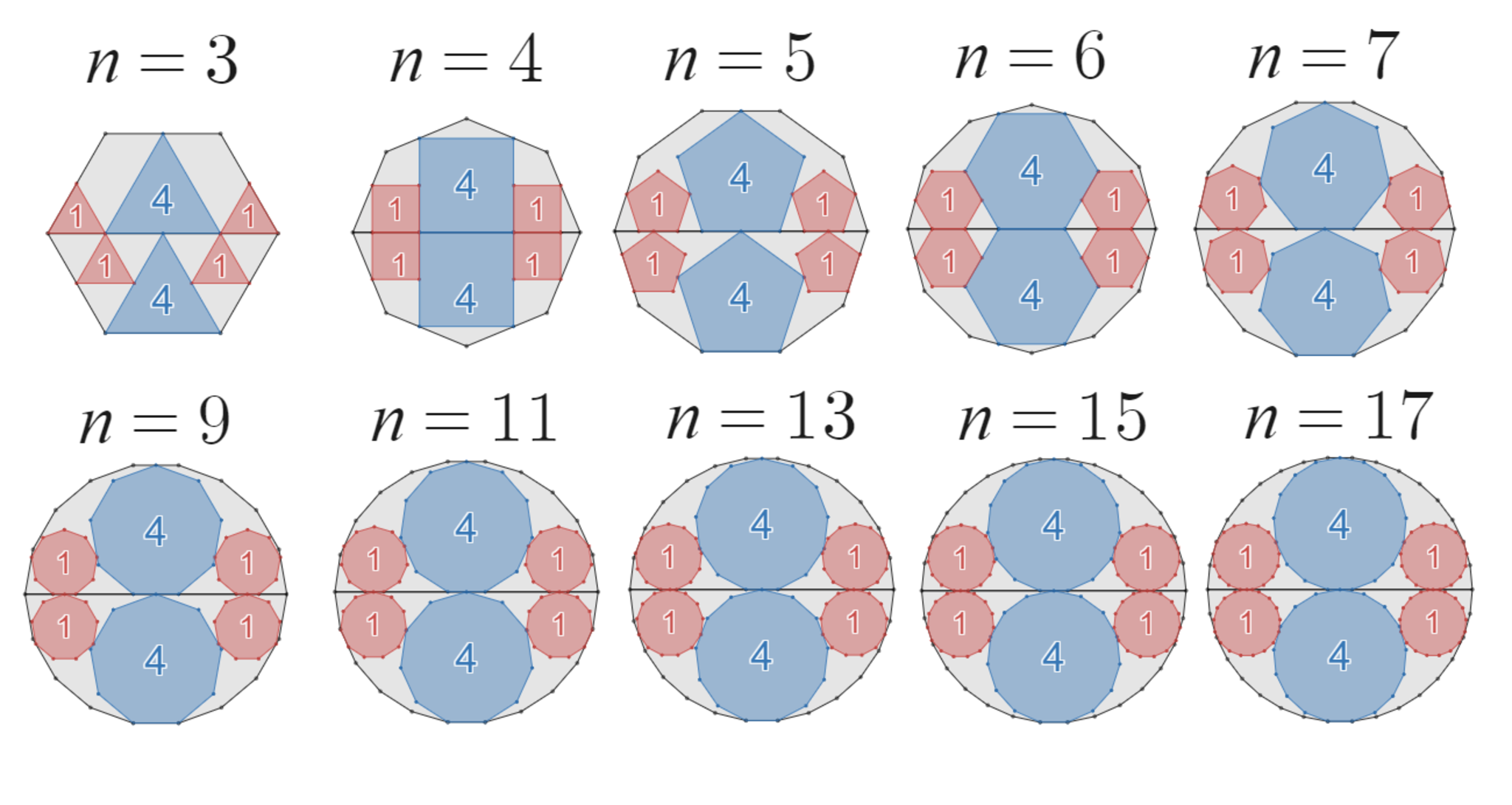具体例

$n$ を $2$ 以上の偶数とする。

$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $4$ の正 $n$ 角形 $A$ を配置する。

$y$ 軸上に中心をもち、辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。

このとき、$B_1$又は$B_2$と外接し、かつ　$x$ 軸とも接するように、「辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接することを示せ。

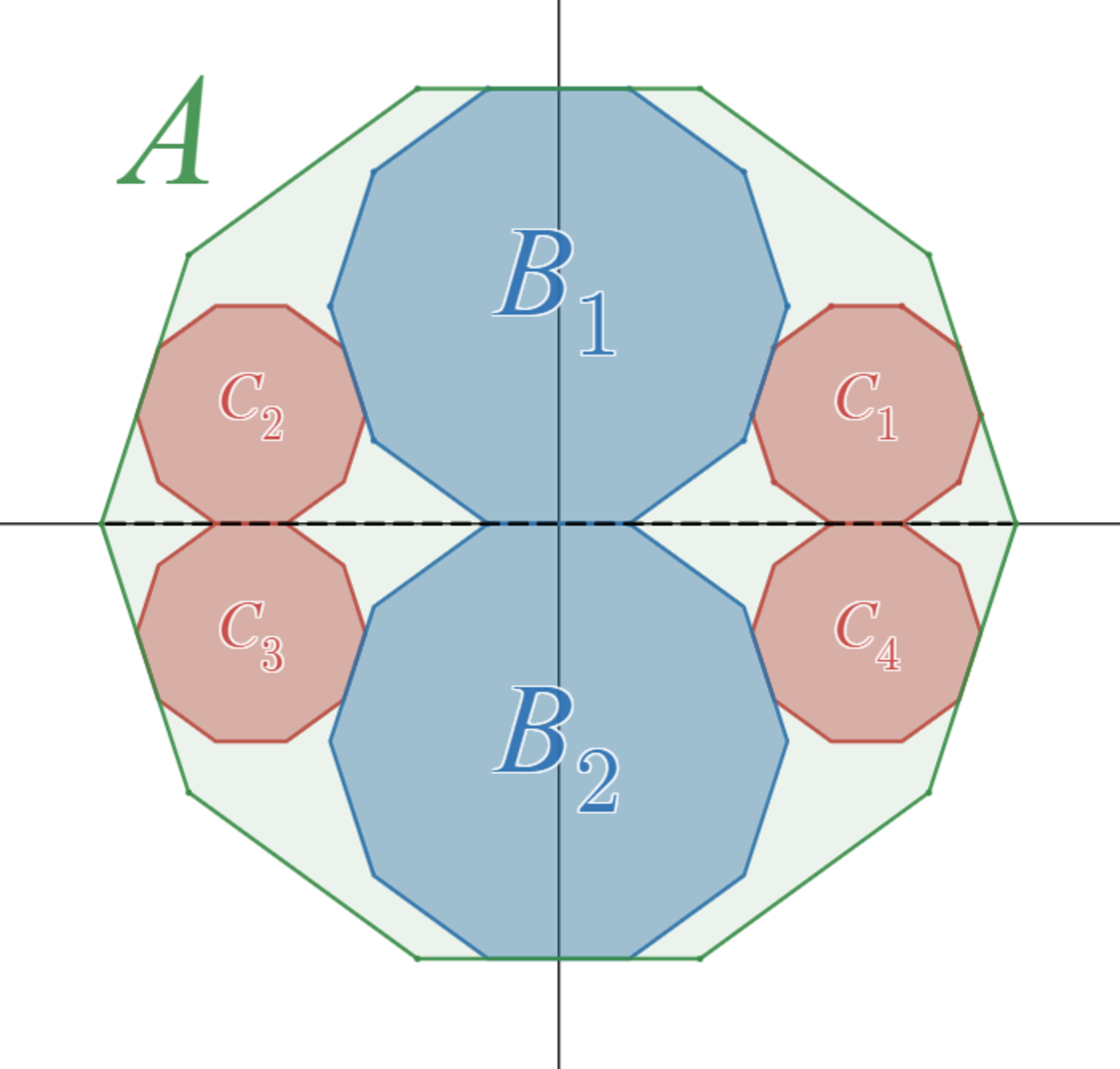相似比2:1の正"偶数"角形内接の定理
※　$C$ の場所は $4$ 箇所あります。区別するため、象限にあわせて $C_1$ ～ $C_4$ と添え字をつけています。

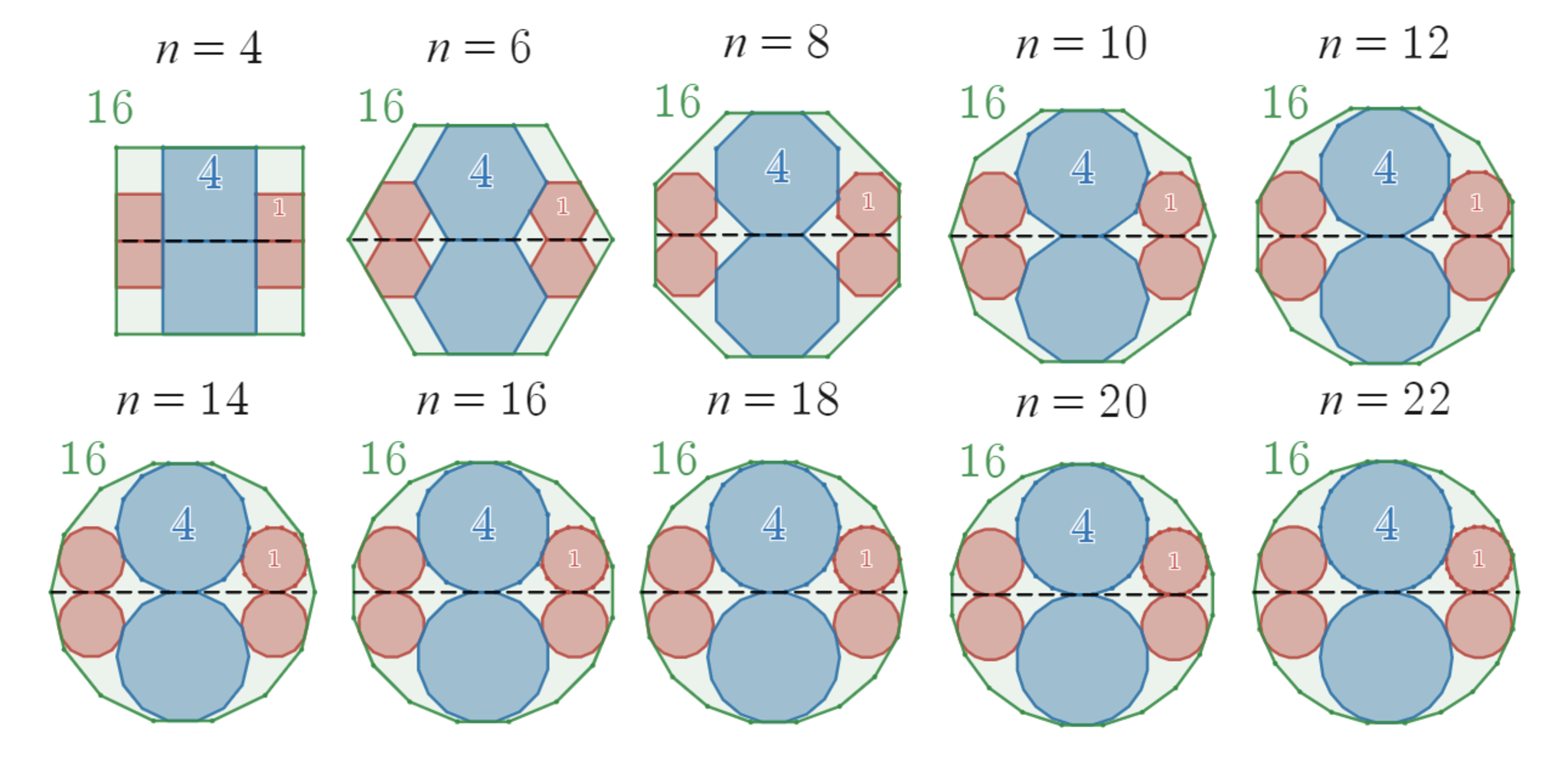具体例

(定理の内容)
「相似比2:1の正"奇数"角形内接の定理」又は「相似比2:1の正"偶数"角形内接の定理」の配置を基準とする。ただし、"奇数"の場合は、$B_2,C_3,C_4$ の位置と角度をそれぞれ $B_1,C_2,C_1$ の $x$ 軸に対する鏡像の位置に変更したものとする。

　基準の位置から始めて、$B_1,B_2,C_1,C_2,C_3,C_4$各パーツが互いに外接している状態を保ちつつ、かつ各パーツが $A$ に内接したまま平行移動することで、各パーツを原点の周りに一周させることができる。

　一周させる間、$B_1,B_2$ と原点は常に一直線上にあるから、その直線と$B_1$(又は$B_2$)の辺のなす角度を任意の角度にすることができる。

(問題)
　この定理の核となる「基準の位置から始めて、$B_1,B_2,C_1,C_2,C_3,C_4$各パーツが互いに外接している状態を保ちつつ、かつ各パーツが $A$ に内接したまま平行移動することで、各パーツを原点の周りに一周させることができる。」の部分を示せ。

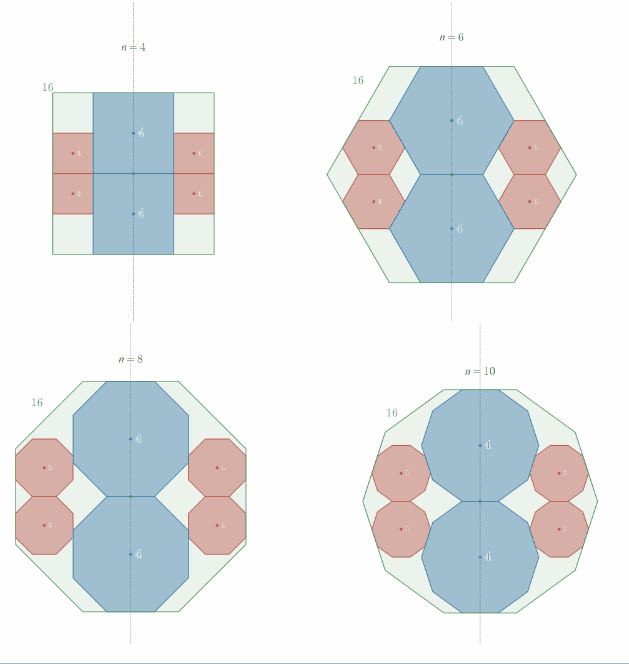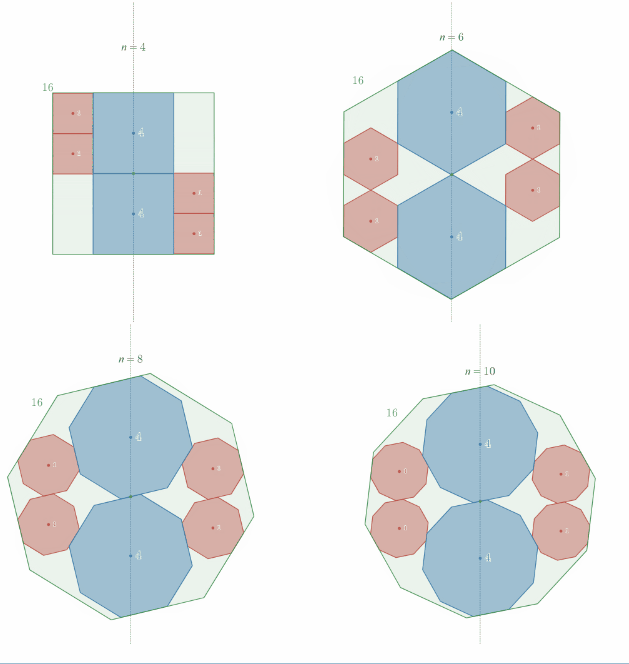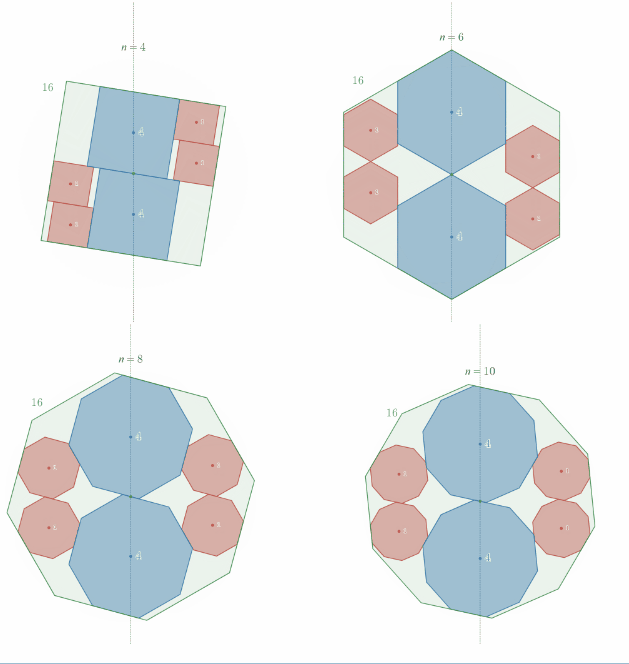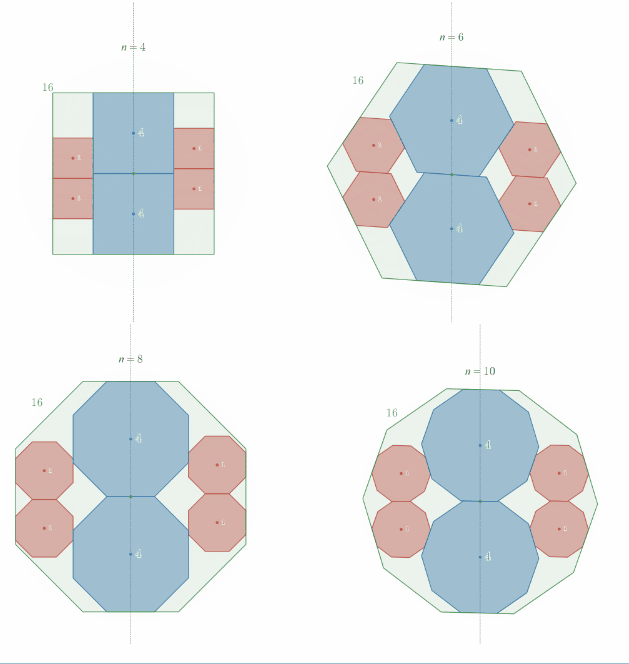相似比2:1の正"偶数"角形内接の定理の一般化 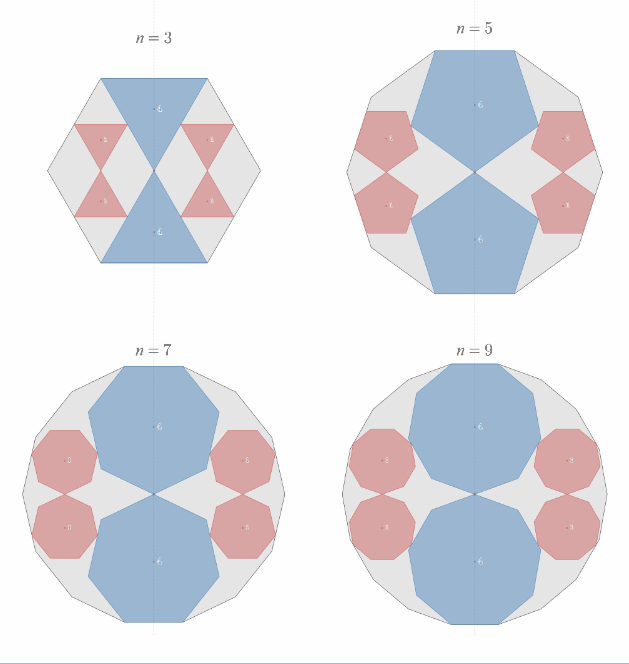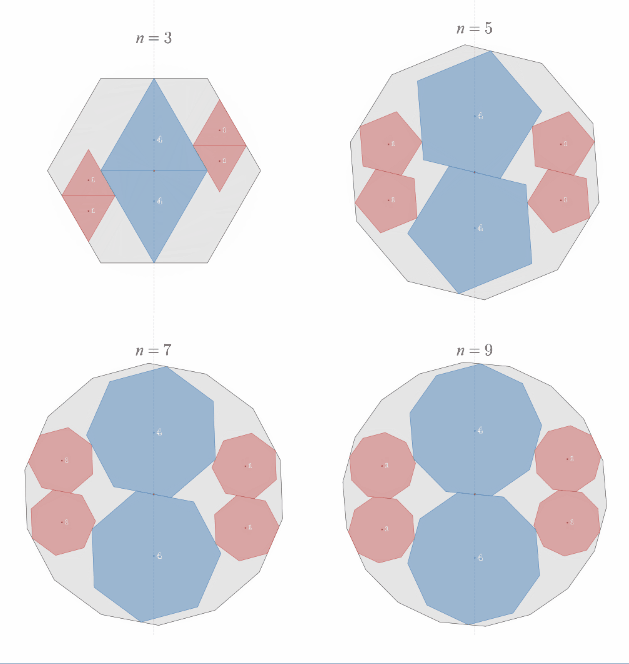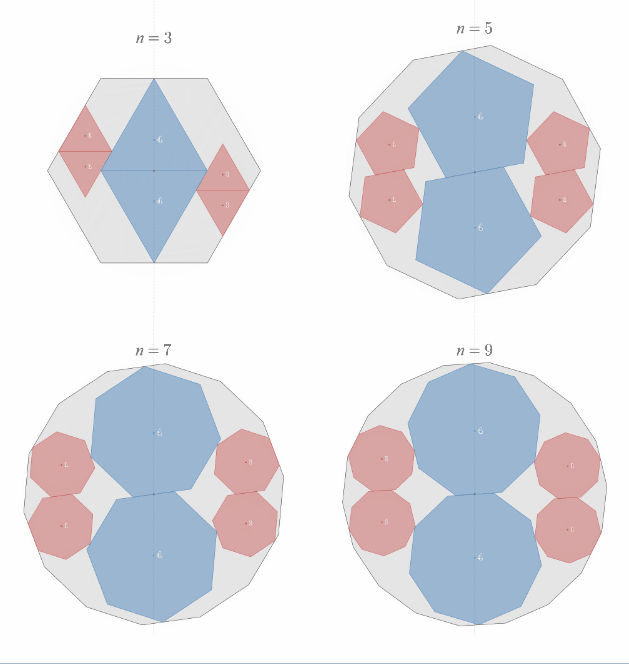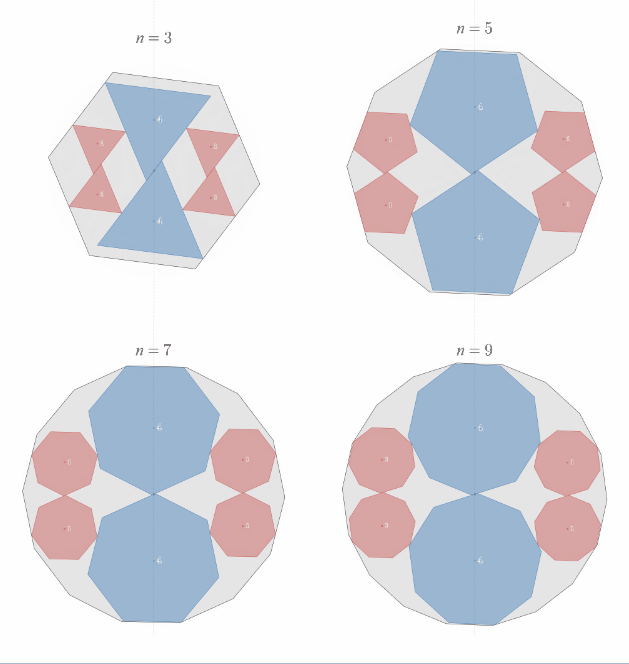相似比2:1の正"奇数"角形内接の定理の一般化

スライドパズルのような平行移動で１回転させることができることを示したい