虚数のエネルギーの遊び方～線型代数でわかるグリーン関数と局所状態密度(LDOS)～

はじめに

　お久しぶりです。東京大学工学部物理工学科B3のYYと申します。今回はphyslab2026アドベントカレンダーとして虚数のエネルギーの遊び方としてグリーン関数および局所状態密度というものを紹介します。
　本記事は11月に駒場理数サークルで投稿しました、 線型代数でわかる有効ハミルトニアン・自己エネルギー・開放量子系 の続編となります。11月の記事を読んでいなくとも読める記事とはなっていますが、読んでいただけると私が嬉しくなります。
　11月の記事では有効ハミルトニアンを導入することで自己エネルギーや開放量子系について考えました。また、ハミルトニアンが非エルミートになることにより虚数のエネルギー固有値が生じることを見ました。

　しかし、そこで求めたエネルギー固有値が果たしてどんな意味を持つのかといった物理学的な考察ができずに終わってしまいました。今回は有効ハミルトニアンによって求まったエネルギー固有値が物理学的にどういう意味を持つ量なのかを深堀していきます。そのための道具として局所状態密度(LDOS)を学びます。
　また局所状態密度(LDOS)による分析を通じてパラメータについて相図が書けるとわかります。相図を通じてパラメータと固有値の物理学的な解釈を与えるのが本記事の最終的な目標です。

問題設定と前回のおさらい

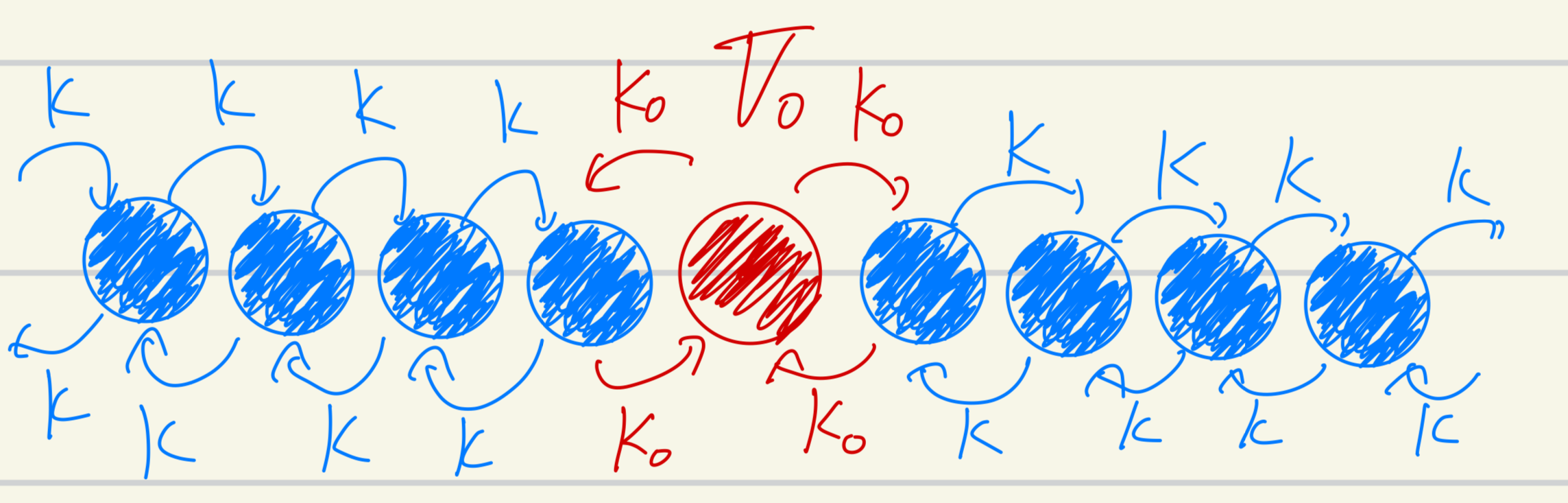不純物モデル
　問題として1次元のタイトバインディング模型を考えます。1次元の格子上に同じ種類の原子が並んでいます。ここで$x=0$のサイトだけ別の原子があるとします（図1)。これは物性の言葉で言えば$x=0$に不純物がある1次元の結晶と言えます。
　$x=0$のサイトのポテンシャルを$V_0$、他のサイトのポテンシャルは$0$とします。またホッピングエネルギーは$x=0$を含むホッピングは$-K_0$、他のホッピングを$-K$とします。するとハミルトニアン$\mathcal{H}$は
$$ \begin{split} \mathcal{H}=&-K\left(\sum_{x=-\infty}^{-2}+\sum_{x=1}^{\infty}\right)(\ket{x}\bra{x+1}+\ket{x+1}\bra{x}) \\ &-K_{0}(\ket{-1}\bra{0}+\ket{0}\bra{-1}+\ket{0}\bra{1}+\ket{1}\bra{0}) \\ &+V_0\ket{0}\bra{0} \end{split} $$
と書けます。
　ここで$V_0=0,K_0=K$としてあげるとモデルは不純物のない綺麗な一次元結晶になります。
　
　そして着目系として$x=0$、環境系として$x\neq0 $を考えると着目系、環境系それぞれの射影演算子$\mathcal{P},\mathcal{Q}$は
$$ \mathcal{P} = \ket{0}\bra{0} $$
$$ \mathcal{Q} = \mathcal{I}-\ket{0}\bra{0} = \left(\sum_{x=-\infty}^{-1}+\sum_{x=1}^{\infty}\right)(\ket{x}\bra{x}) $$
となりました。

　すると着目系$P$の有効ハミルトニアン$ \mathcal{H}_{\mathrm{eff}}(\mathscr{E})$と自己エネルギー$G(\mathscr{E})$は
$$ \mathcal{H}_{\mathrm{eff}}(\mathscr{E})=\left(V_0+2K^{2}_{0}G(\mathscr{E})\right)\ket{0}\bra{0} $$
$$ G(\mathscr{E})=\bra{1}\frac{1}{\mathscr{E}+K\sum_{x=1}^{\infty}\left(\ket{x}\bra{x+1}+\ket{x+1}\bra{x}\right)}\ket{1} $$
$$ K^2G(\mathscr{E})^2-\mathscr{E}G(\mathscr{E})+1 =0 $$
となりました。ここで$\mathscr{E}$はエネルギーです。つまり有効ハミルトニアンはエネルギー$\mathscr{E}$の関数になるのでした。

　そしてエネルギー固有値を求めるという作業は自己無撞着かつ非線型な固有値方程式
$$ \mathcal{H}_{\mathrm{eff}}(\mathscr{E})\ket{\psi}=\mathscr{E}\ket{\psi} $$
という方程式を解くことになるのでした。

　以下では本章で定義した文字は断りなく用います。

グリーン関数

　さて、おさらいも済んだので今回の主題である局所状態密度(LDOS)を導入していきたいのですが、その前にグリーン関数を学びます。

グリーン関数・遅延グリーン関数・先進グリーン関数

素朴には
$$ \mathcal{G}(\mathscr{E})=\frac{1}{\mathscr{E}-\mathcal{H}} $$
ですが$\mathscr{E}-\mathcal{H}=0$となり発散してしまう可能性があります。そこで$\mathscr{E}-\mathcal{H}=0$となってもいいように虚軸へずらすという操作を行います。

$\mathscr{E}$は実数のため$\mathscr{E}-\mathcal{H}\pm i\eta\neq0$となり発散を防ぐことができます。ここで導入した$\mathcal{G}^{\mathrm{R}}(\mathscr{E})$を遅延グリーン関数、$\mathcal{G}^{\mathrm{A}}(\mathscr{E})$を先進グリーン関数といいます。
　複素関数論や物理学における因果律の議論によると通常物性等で活用する場合は遅延グリーン関数$\mathcal{G}^{\mathrm{R}}(\mathscr{E})$をグリーン関数として採用します。以下では$\mathcal{G}^{\mathrm{R}}(\mathscr{E})$を単に$\mathcal{G}(\mathscr{E})$と書き、
$$ \mathcal{G}(\mathscr{E})=\frac{1}{\mathscr{E}-\mathcal{H}+i\eta} $$
とします。

行列表示

　グリーン関数は演算子のため任意の完全正規直交系(CONS)によって行列として扱うことできます。ここでは完全正規直交系(CONS)としてサイトの状態ケット$\left\{\ket{x}\right\}$を採用します。
$$ \mathcal{I}=\sum_x\ket{x}\bra{x}=\mathcal{P}+\mathcal{Q} $$
$$ \mathcal{P}=\mathcal{P}^2,\mathcal{Q}=\mathcal{Q}^2,\mathcal{P}\mathcal{Q}=0 $$
に留意し、
$$ \begin{split} \mathcal{I} &=(\mathscr{E}-\mathcal{H})\mathcal{G}(\mathscr{E})\\ &=\mathcal{I}(\mathscr{E}-\mathcal{H})\mathcal{I}\mathcal{G}(\mathscr{E})\mathcal{I}\\ &=(\mathcal{P}+\mathcal{Q})(\mathscr{E}-\mathcal{H})(\mathcal{P}^2+\mathcal{Q}^2)\mathcal{G}(\mathscr{E})(\mathcal{P}+\mathcal{Q})\\ &= \begin{pmatrix} \mathscr{E}-\mathcal{P}\mathcal{H}\mathcal{P} & -\mathcal{P}\mathcal{H}\mathcal{Q}\\ -\mathcal{Q}\mathcal{H}\mathcal{P} & \mathscr{E}-\mathcal{Q}\mathcal{H}\mathcal{Q} \\ \end{pmatrix} \begin{pmatrix} \mathcal{P}\mathcal{G}(\mathscr{E})\mathcal{P} & \mathcal{P}\mathcal{G}(\mathscr{E})\mathcal{Q}\\ \mathcal{Q}\mathcal{G}(\mathscr{E})\mathcal{P} & \mathcal{Q}\mathcal{G}(\mathscr{E})\mathcal{Q} \\ \end{pmatrix} \end{split} $$
このようにブロック行列により表現できます。これはグリーン関数$\mathcal{G}(\mathscr{E})$の4つのブロックについての4元連立方程式のため代数的な計算により解くことができます。すると着目系についてのブロック$\mathcal{P}\mathcal{G}(\mathscr{E})\mathcal{P}$は
$$ \begin{split} \mathcal{P}\mathcal{G}(\mathscr{E})\mathcal{P} &=\frac{1}{\mathscr{E}-\mathcal{P}\mathcal{H}\mathcal{P}-\mathcal{P}\mathcal{H}\mathcal{Q}\frac{1}{\mathscr{E}-\mathcal{Q}\mathcal{H}\mathcal{Q}}\mathcal{Q}\mathcal{H}\mathcal{P}+i\eta}\\ &=\frac{1}{\mathscr{E}-\mathcal{H}_{\mathrm{eff}}(\mathscr{E})+i\eta} \end{split} $$
と書けます。
　今回の場合、
$$ \mathcal{P}=\ket{0}\bra{0} $$
のため
$$ \mathcal{P}\mathcal{G}(\mathscr{E})\mathcal{P}=\bra{0}\mathcal{G}(\mathscr{E})\ket{0}\ket{0}\bra{0} $$
と表せます。以上の議論より
$$ \mathcal{G_{00}(\mathscr{E})}=\bra{0}\mathcal{G}(\mathscr{E})\ket{0} $$
とすることで、
$$ \mathcal{G_{00}(\mathscr{E})}=\bra{0}\frac{1}{\mathscr{E}-\mathcal{H}+i\eta}\ket{0}=\frac{1}{\mathscr{E}-\mathcal{H}_{\mathrm{eff}}(\mathscr{E})+i\eta} $$
となります。最右辺は今回のサイト基底を取った場合は$\mathcal{H}_{\mathrm{eff}}$が$1\times1$行列で表現できもはやスカラーとして扱えるためこう書いています。

局所状態密度(LDOS)とは？

　さて、おさらいも済んでグリーン関数も理解できたので今回の主題である局所状態密度(LDOS)を導入していきましょう。

複素関数論の公式

　本記事ではなるべく高度な数学は使いたくなのですが、これだけは使わせてください。複素関数論の有名な公式として以下の公式があります。

$\mathscr{P}\frac{1}{x}$は主値積分を表す実数です。今回は実数に用はないため何か実数の量だと思ってください。大事なのは虚部です。虚部はデルタ関数となります。これがグリーン関数と局所状態密度を密接に関連付けてくれます。

グリーン関数と局所状態密度(LDOS)

　さて本題です。グリーン関数$\mathcal{G_{00}(\mathscr{E})}$を考えます。ハミルトニアン$\mathcal{H}$の固有ケットを$\ket{n}$とします。固有ケットは完全正規直交系(CONS)をなすため
$$ \mathcal{I}=\sum_{n}\ket{n}\bra{n} $$
$$ \bra{m}\mathcal{H}\ket{n}=\mathscr{E}_n \delta_{mn} $$
となります。これらを利用して変形していきます。
$$ \begin{split} \mathcal{G_{00}(\mathscr{E})} &=\bra{0}\mathcal{I}\frac{1}{\mathscr{E}-\mathcal{H}+i\eta}\mathcal{I}\ket{0}\\ &=\bra{0}\sum_m\ket{m}\bra{m}\frac{1}{\mathscr{E}-\mathcal{H}+i\eta}\sum_n\ket{n}\bra{n}\ket{0}\\ &=\sum_{mn}\bra{0}\ket{m}\frac{1}{\mathscr{E}-\mathscr{E}_m\delta_{mn}+i\eta}\bra{n}\ket{0}\\ &=\sum_{n}\abs{\bra{0}\ket{n}}^2\frac{1}{\mathscr{E}-\mathscr{E}_n+i\eta}\\ &=\sum_n\abs{\bra{0}\ket{n}}^2\left[\mathscr{P}\frac{1}{\mathscr{E}-\mathscr{E}_n}-i\pi\delta\left(\mathscr{E}-\mathscr{E}_n\right) \right] \end{split} $$
ここで局所状態密度(LDOS)$\mathcal{A}_0(\mathscr{E})$を以下のように定義します。

するとグリーン関数$\mathcal{G_{00}(\mathscr{E})}$と局所状態密度(LDOS)$\mathcal{A}_0(\mathscr{E})$の重要な公式を得ます。

局所状態密度(LDOS)とはなにか？

$\mathcal{A}_0(\mathscr{E})$はサイト$0$における状態$\ket{n}$の確率分布$\abs{\bra{0}\ket{n}}^2$を重みとしてデルタ関数$\delta\left(\mathscr{E}-\mathscr{E}_n\right)$を足し合わせた式になっています。この関数の性質を見るために全エネルギーにわたっての積分を求めます。
$$ \begin{split} \int_{-\infty}^{\infty} d\mathscr{E}\mathcal{A}_0(\mathscr{E}) &=\sum_n\abs{\bra{0}\ket{n}}^2\int_{-\infty}^{\infty} d\mathscr{E}\delta\left(\mathscr{E}-\mathscr{E}_n\right)\\ &=\sum_n\abs{\bra{0}\ket{n}}^2\\ &=\bra{0}\sum_n\ket{n}\bra{n}\ket{0}\\ &=\bra{0}\ket{0}\\ &=1 \end{split} $$
つまり全エネルギーにわたっての積分が$1$となります。したがってこの関数はサイト$0$において電子のエネルギー状態密度がどのような分布になっているかを表現しているといえます。エネルギー状態密度というのはざっくりと言えばあるエネルギーを持った電子が座れる座席の数です。全エネルギーの積分が$1$となるのは「サイト$0$に電子が1個存在できること」を表します。この状態密度が大きいほど電子はそのエネルギーに存在しやすくなることを表し、状態密度が$0$ならば電子はそのエネルギーに存在できません。

LDOSで遊ぼう

　では今回は不純物モデルのLDOSを味わいましょう。

自己エネルギーの決定

$$ \begin{split} \mathcal{G_{00}(\mathscr{E})} &=\bra{0}\frac{1}{\mathscr{E}-\mathcal{H}+i\eta}\ket{0}\\ &=\frac{1}{\mathscr{E}-\mathcal{H}_{\mathrm{eff}}(\mathscr{E})+i\eta}\\ &=\frac{1}{\mathscr{E}-V_0-2K^{2}_{0}G(\mathscr{E})+i\eta} \end{split} $$
　$\mathcal{G_{00}(\mathscr{E})}$の関数形を決定するため自己エネルギー$2K^{2}_{0}G(\mathscr{E})$を導くグリーン関数$G(\mathscr{E})$を決定しに行きます。
$$ K^2G(\mathscr{E})^2-\mathscr{E}G(\mathscr{E})+1 =0 $$
これを解くと
$$ \begin{split} G(\mathscr{E}) &=\frac{\mathscr{E}\pm\sqrt{\mathscr{E}^2-4K^2}}{2K^2}\\ &=\frac{1}{2K}\left(\frac{\mathscr{E}}{K}\pm\sqrt{\left(\frac{\mathscr{E}}{K}\right)^2-4}\right) \end{split} $$
と2つの答えが出ます。どちらを採用するか決定します。

自己エネルギーが虚数の場合

$$ -2K<\mathscr{E}<2K $$
の場合自己エネルギーが虚数になります。
$$ G(\mathscr{E})=\frac{1}{2K}\left(\frac{\mathscr{E}}{K}\pm i \sqrt{4-\left(\frac{\mathscr{E}}{K}\right)^2}\right) $$
ここで出た2つの解は虚部が正のほうが先進グリーン関数、虚部が負のほうが遅延グリーン関数に相当します。ここでは虚部が負のほうの遅延グリーン関数を採用します。

自己エネルギーが実数の場合

$$ \mathscr{E}\le-2K,2K\le\mathscr{E} $$
の場合自己エネルギーが実数になります。
$$ G(\mathscr{E})=\frac{1}{2K}\left(\frac{\mathscr{E}}{K}\pm \sqrt{\left(\frac{\mathscr{E}}{K}\right)^2-4}\right) $$
自己エネルギーが実数の場合虚部が存在しないため先進グリーン関数も遅延グリーン関数も一緒になります。したがって導かれた2つの解の内一方がグリーン関数であり、もう一方はグリーン関数になりません。
　ここで自己エネルギーを導くグリーン関数$G(\mathscr{E})$が
$$ G(\mathscr{E})=\bra{1}\frac{1}{\mathscr{E}+K\sum_{x=1}^{\infty}\left(\ket{x}\bra{x+1}+\ket{x+1}\bra{x}\right)}\ket{1} $$
と定義されていたことを思い出します。すると$\mathscr{E}\rightarrow\pm\infty$に対し$G(\mathscr{E})$は$\frac{1}{\mathscr{E}}$に漸近します。従って$\mathscr{E}\rightarrow\pm\infty$に対して$G(\mathscr{E})$は$0$に収束します。
　これに注意すると自己エネルギーが実数の場合、自己エネルギーを導くグリーン関数$G(\mathscr{E})$は符号関数$\mathrm{sign}(x)$を用いて
$$ G(\mathscr{E})=\frac{1}{2K}\left(\frac{\mathscr{E}}{K}-\mathrm{sign}(\mathscr{E})\sqrt{\left(\frac{\mathscr{E}}{K}\right)^2-4}\right) $$
となります。

無次元化

　結果を解析するために物理量を無次元化します。具体的には結晶のホッピングエネルギー$K$を基準として
$$ v=\frac{V_0}{K},k=\frac{K_0}{K},\epsilon=\frac{\mathscr{E}}{K} $$
と無次元パラメータを導入します。すると局所状態密度$\mathcal{A}_0(K\epsilon)$は
$$ \mathcal{A}_0(K\epsilon)=-\frac{1}{\pi K}\Im\left(\frac{1}{\epsilon-v-2k^2 g(\epsilon)+i\eta}\right) $$
ただし$g(\epsilon)$は無次元化されたグリーン関数であり
$$ g(\epsilon)= \begin{dcases} \frac{1}{2}\left(\epsilon+\sqrt{\epsilon^2-4}\right) & (\epsilon \le-2) \\ \frac{1}{2}\left(\epsilon-i\sqrt{4-\epsilon^2}\right) & (-2<\epsilon <2) \\ \frac{1}{2}\left(\epsilon-\sqrt{\epsilon^2-4}\right) & (2\le\epsilon) \\ \end{dcases} $$

LDOSをみる

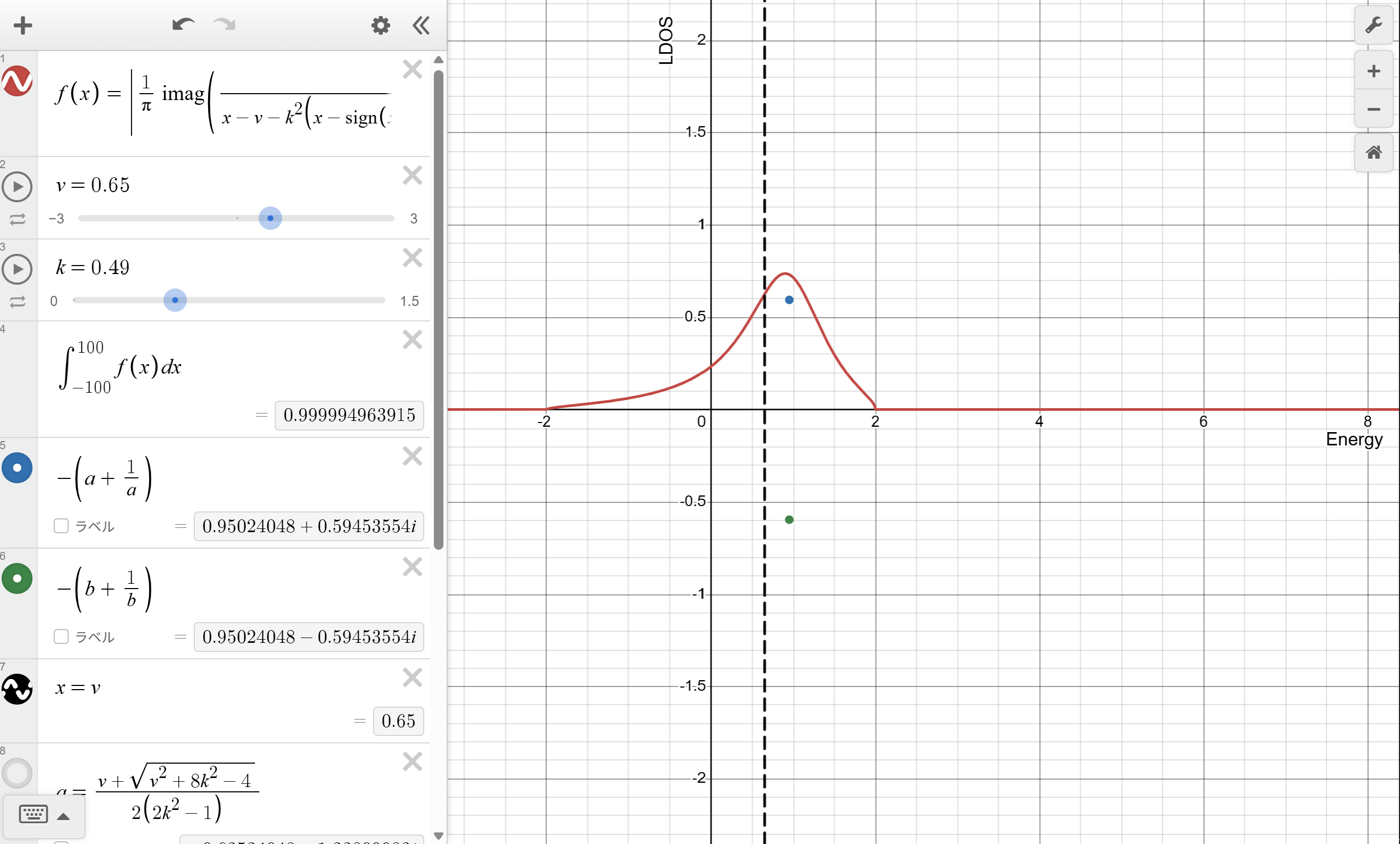虚数固有値があるときのLDOS
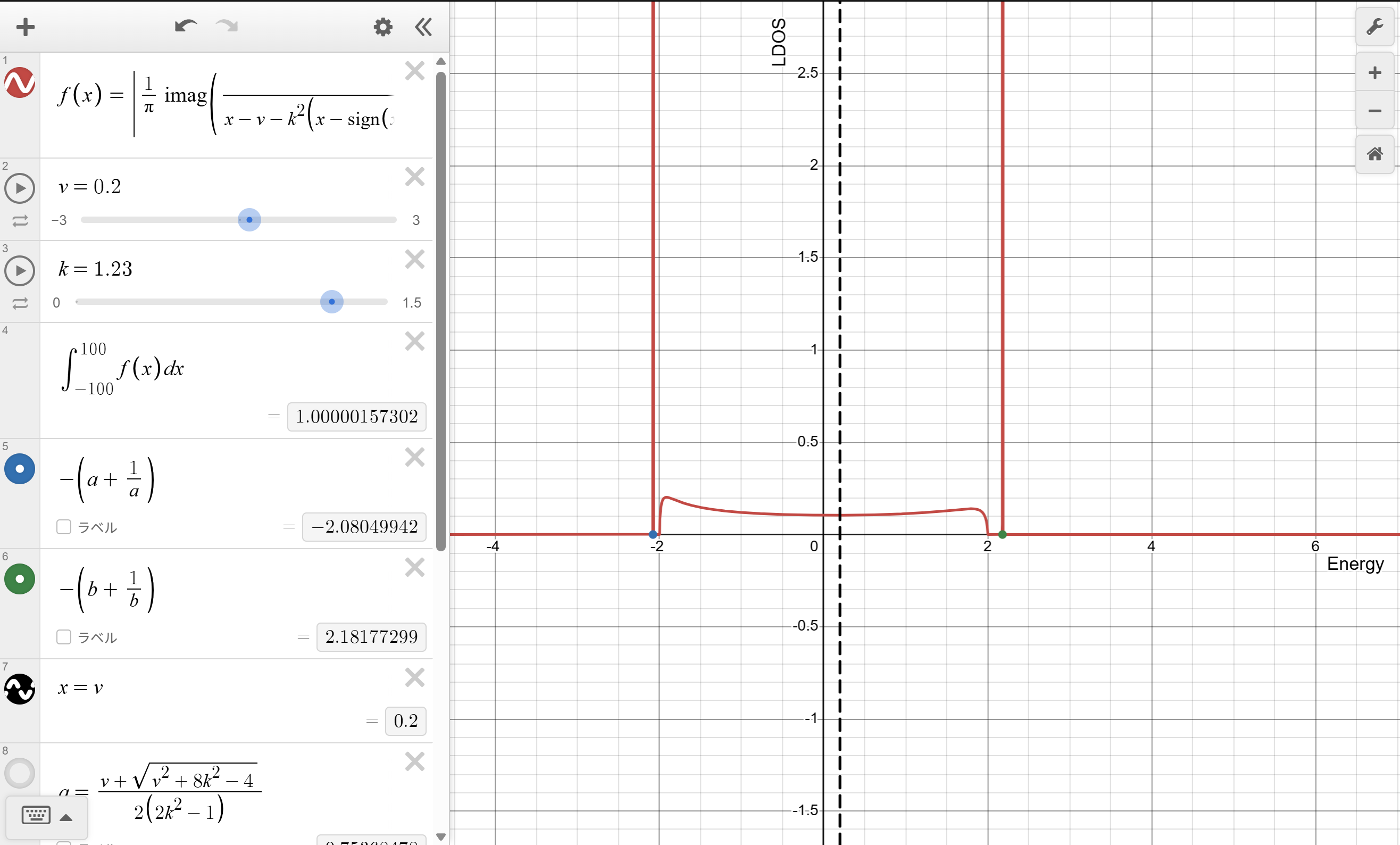ピークがあるときのLDOS
　$K=1$として DESMOSでplot しました。赤い曲線がLDOSで、横軸がエネルギー$\epsilon$縦軸がLDOS$\mathcal{A}_0(\epsilon)$です。グラフ上の青と緑の点は有効ハミルトニアン$\mathcal{H}_{\mathrm{eff}}$のエネルギー固有値であり横軸が実軸、縦軸が虚軸の複素平面としてplotしています。また黒い点線はサイト$0$のポテンシャル$v$を表します。
　関数設定内の積分はLDOSのエネルギー積分です。ほぼ1になっていることが確認できます。

LDOSを解析する

　いくつか特徴的な場合のLDOSのプロットを紹介します。

$k=1,v=0$(不純物なし)

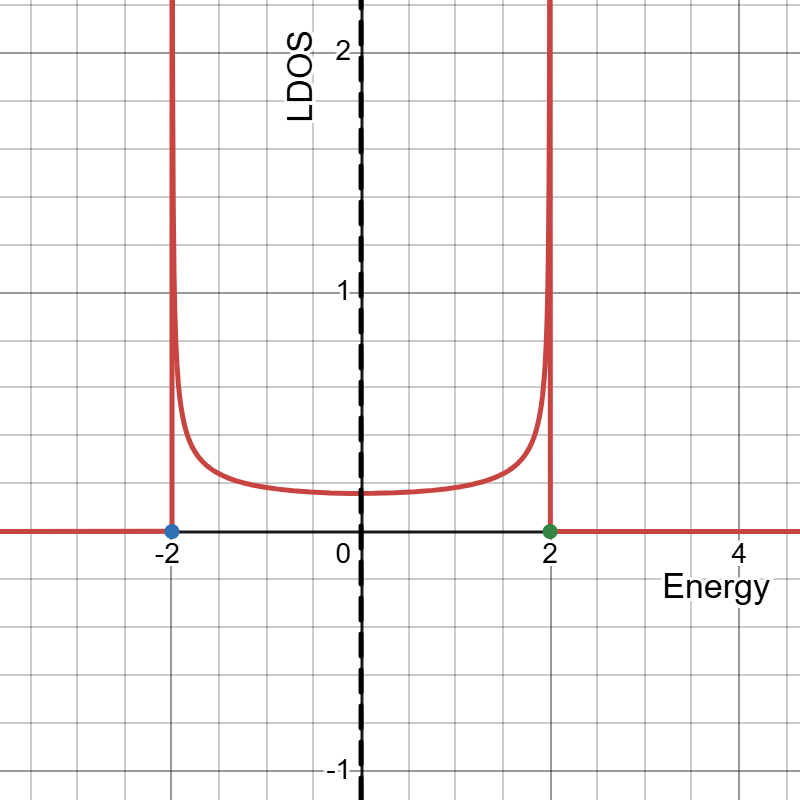不純物なしLDOS
　$k=1,v=0$とするとサイト0の原子が他のサイトと等価、つまり不純物のない1種類原子からなる1次元結晶となります。図4のLDOSは1次元の1種類原子からなるタイトバインディング模型の状態密度と一致しています。このとき有効ハミルトニアンの固有値は状態密度の発散点$\epsilon=-2,2$に一致しています。
　ここで特徴的なのは$-2\le\epsilon\le2$にわたって連続スペクトルが生じている点です。この連続スペクトルのことを物性論ではバンドと言います。このバンドのエネルギー密度が不純物の効果によってどう変化するかを見ていきます。

k=0(不純物が孤立)

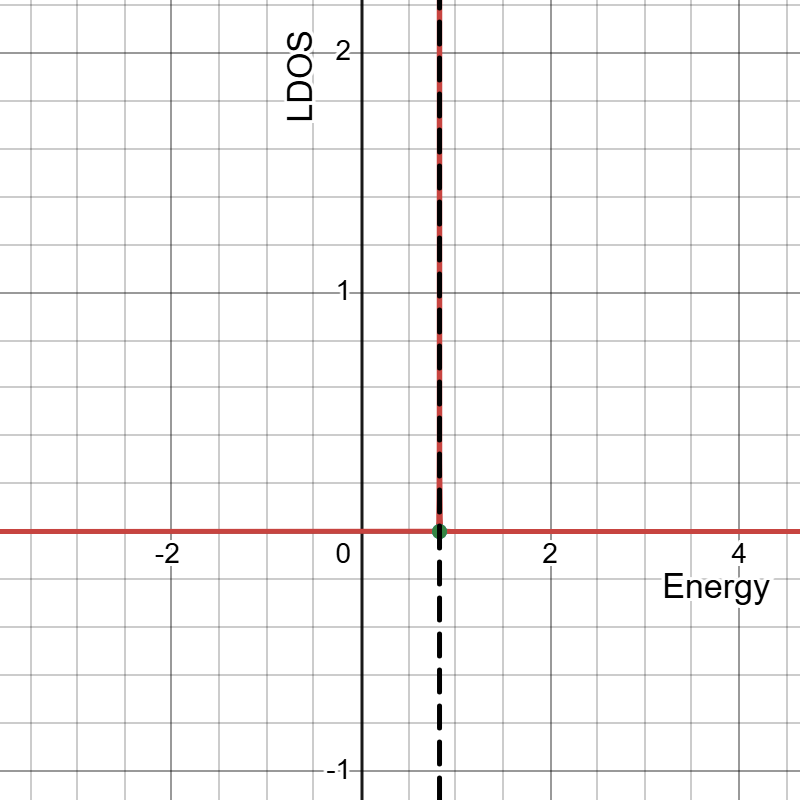孤立LDOS
　$k=0$とすると不純物と周りの結晶との相互作用がなくなり不純物が孤立します。するとバンドは消滅しLDOSは不純物のポテンシャル$v$のみに値をもつスペクトルとなります。このとき有効ハミルトニアンの2つの固有値はともに$v$に一致します。強調したい文字

2ピーク(束縛・束縛)

束縛・束縛LDOS($k=1.5,v=0.4$)
　有効ハミルトニアンの固有値がともに実軸かつバンド($-2\le\epsilon\le2$)の外にあり、さらにエネルギー固有値の箇所にLDOSのピーク線が生じています。このようにエネルギー固有値にLDOSのピーク線が生じている状態を束縛状態と言います。電子がサイト0固有のエネルギー状態に束縛されている状態です。
　このエネルギー固有値はともにサイト0のポテンシャル$v$から大きくずれています。このずれがくりこみによって生じた自己エネルギー分のエネルギーのずれです。

1ピーク(束縛・反束縛)

束縛・反束縛LDOS($k=0.9,v=-1.48$)
束縛・反束縛LDOS($k=0.9,v=1.48$)
　有効ハミルトニアンの固有値がともに実軸かつバンド($-2\le\epsilon\le2$)の外にありますが、1つの固有値はピーク線が生じ1つの固有値はピーク線が生じていません。このピーク線が生じていないが実軸上に固有値がある状態を反束縛状態といいます。これはそこにサイト0固有のエネルギー状態の準位はあるがサイト0以外の環境系に電子が束縛されてしまっている状態を表します。

0ピーク(反束縛・反束縛)

反束縛・反束縛LDOS($k=0.85,v=-0.01$)
　ピーク線が生じずともに反束縛状態となっている場合です。

虚数エネルギー(共鳴・反共鳴)

共鳴・反共鳴($k=0.41,v=0.6$)
　有効ハミルトニアンのエネルギー固有値が虚数となっています。さらに固有値がバンド($-2\le\epsilon\le2$)に侵入することができるようになっています。この虚数エネルギーの状態を共鳴・反共鳴状態といいます。虚部が正のほうが共鳴状態、負のほうが反共鳴状態に対応します。これはサイト$0$固有のエネルギーが環境のエネルギーであるバンド($-2\le\epsilon\le2$)に侵入することで電子がサイト$0$と環境系で流出入している状態を表します。
　また有効ハミルトニアンのエネルギー固有値が虚数となるためピークが鋭くならず広がりが生じます。実際この時、LDOS$\mathcal{A}_0(\mathscr{E})$は
$$ \begin{split} \mathcal{A}_0(\mathscr{E}) &=-\frac{1}{\pi}\Im\left(\frac{1}{\mathscr{E}-V_0-2K^{2}_{0}(\Re G(\mathscr{E})+i\Im G(\mathscr{E}))}\right)\\ &=\frac{1}{\pi}\frac{-2K_0^2\Im G(\mathscr{E})}{(\mathscr{E}-V_0-2K^{2}_{0}\Re G(\mathscr{E}))^2+(2K^{2}_{0}\Im G(\mathscr{E}))^2} \end{split} $$
というローレンツ型の分布になります。

特異帯$k=\frac{1}{\sqrt{2}}$

束縛状態($v=1.64$)
反束縛状態($v=0.32$)
固有値発散($v=0$)
　$k=\frac{1}{\sqrt{2}}$では有効ハミルトニアンの解がただ一つとなる特異現象が生じます。これは数学的には解を求める二次方程式の二次の係数が$0$になってしまっている状態で重解ではなく正真正銘に一つのみの解です。さらに$v=0$では固有値が発散します。
　状態としては束縛状態、反束縛状態、固有値発散(分類上は反束縛状態)があります。

まとめとパラメータ相図

　局所状態密度(LDOS)の解析により有効ハミルトニアンの固有値はスペクトルのピークに関する量であることがわかりました。
　またパラメータの取り方によってLDOSが大きく変化します。この様子をまとめたのが以下の相図です。
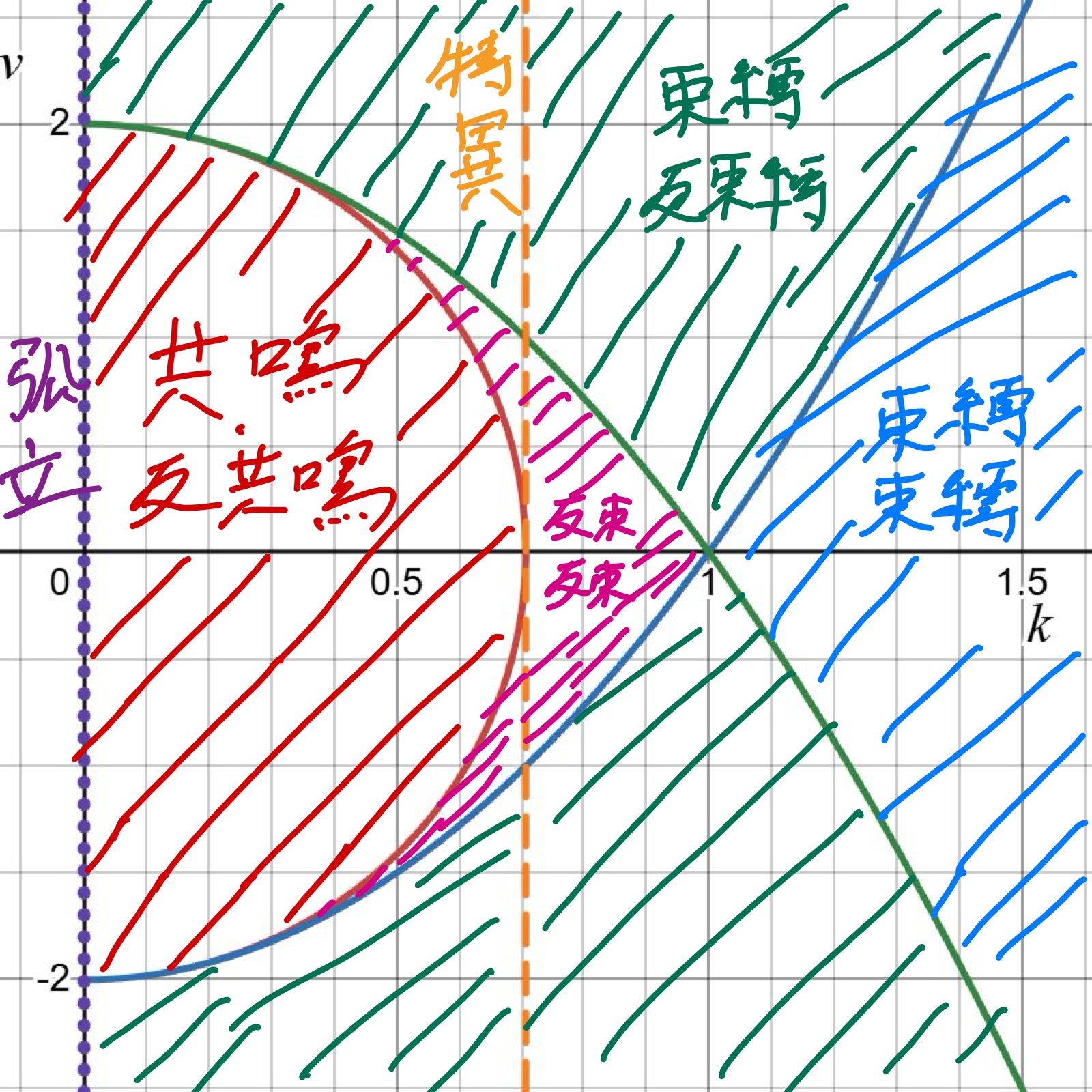パラメータ相図
　横軸がサイト$0$と環境系の相互作用の強さを表す$k$,縦軸をサイト$0$のポテンシャル$v$でとっています。$K_0$が$K$に等しくなる$k=1$を境に束縛・束縛状態と反束縛・反束縛状態が分かれ、特異帯$k=\frac{1}{\sqrt{2}}$を境に共鳴・反共鳴状態が現れます。環境との相互作用が弱くなるほど束縛から反束縛、共鳴へと状態が移り変わっていくことがわかります。
　またポテンシャルの絶対値が大きいほど束縛・反束縛状態に近づいていくことがわかります。