6元集合に入る結合律を満たさない演算
6元集合に入る結合律を満たさない演算
クラインの四元群という群の例がある。前の記事「
同じ集合が異なる演算で群となる例
」で、$\{0,1,2,3\}$に入る演算で、それらの組が群になって、クラインの四元群と同型になる例をあげた。それを拡張しようとして、$6$元集合$\{0,1,2,3,4,5\}$に定まる演算を考えてみた。この演算に関して、群の公理を確かめたところ、そのうち結合律だけが成り立たないことが分かった。
それが役に立つものであるかどうかはわからないが、何かが群になるかを確かめるとき、結合律を満たす事が大切である事の例になるかと思うので紹介しようと思う。
位数の小さい有限集合とその演算の演算結果を表の形にした乗積表(加法表、群表)があると、他の群の公理は割と簡単に確かめられるのに対して、結合律は簡単には確かめられない。
また、他の群の公理を確かめたからと言って、結合律を満たすとは限らない。実際満たさない例である。
群の定義等は前の記事「 同じ集合が異なる演算で群となる例 」を参照。
その演算の定義
$S=\{0,1,2,3,4,5\} $の$2$つの数から、$S$の$1$つの数$x \oplus y $を定める。
$x,y \in S;x \oplus y \in S$
- $0$と他の元$x$の演算結果は$x$とする。
$x \oplus 0 = 0 \oplus x = x$ - $x$と同じ元$x$の演算結果は$0$とする。
$x \oplus x = 0$ - 平面上に正5角形を書いて、頂点に$1,2,3,4,5$のラベルを付与する。
$x ,y \in S-\{0\}$に対して、対応する$2$つの頂点から平面上同じ距離にある頂点のラベル$z$で$x\oplus y≝z$と定義する。
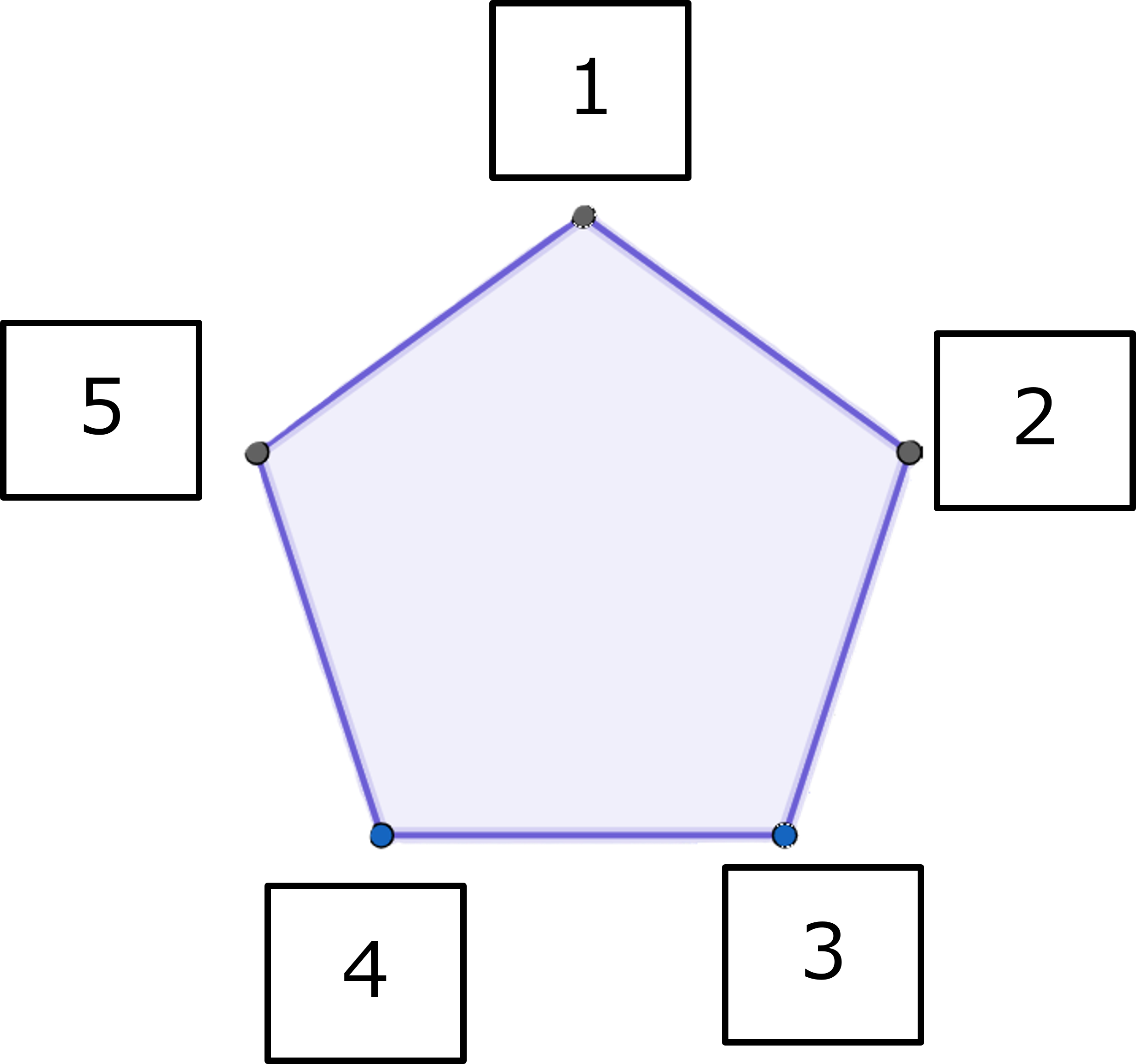 正5角形とラベル
正5角形とラベル
乗積表(加算表)を作成する
定義だけだとわかりづらいと思うので、乗積表を作成する。
[1]より、$0$の列と$0$の行は、それぞれヘッダーにある数が入る。
[2]より、左上から右下の対角線の部分は$0$が入る。
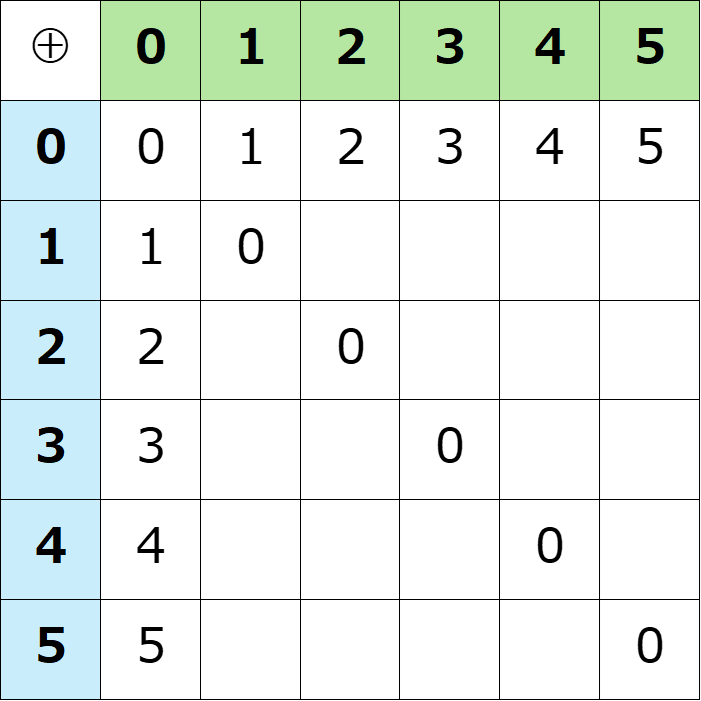 乗積表:0の行と列と対角線
乗積表:0の行と列と対角線
$0$以外の元の異なる元$2$つについて、$1$つ$1$つどうなるかを見る。
まず、
$1$と$2$については、$4$(そして$4$だけが)が等距離にあるとわかるので
$1 \oplus 2 =2 \oplus 1=4$
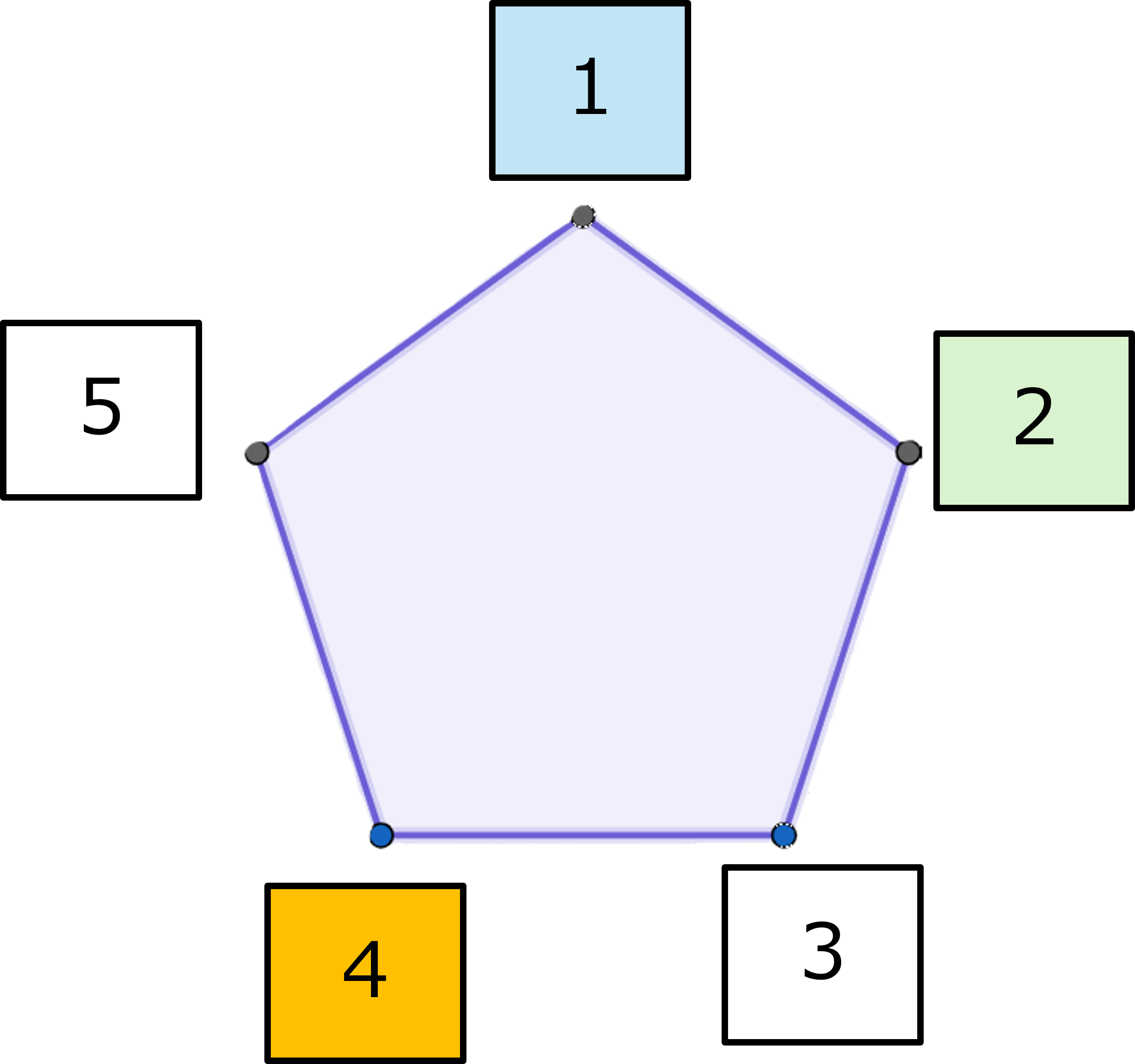 1⊕2=2⊕1=4
1⊕2=2⊕1=4
$1$と$3$については、$2$(そして$2$だけが)が等距離にあるとわかるので
$1 \oplus 3 =3 \oplus 1=2$
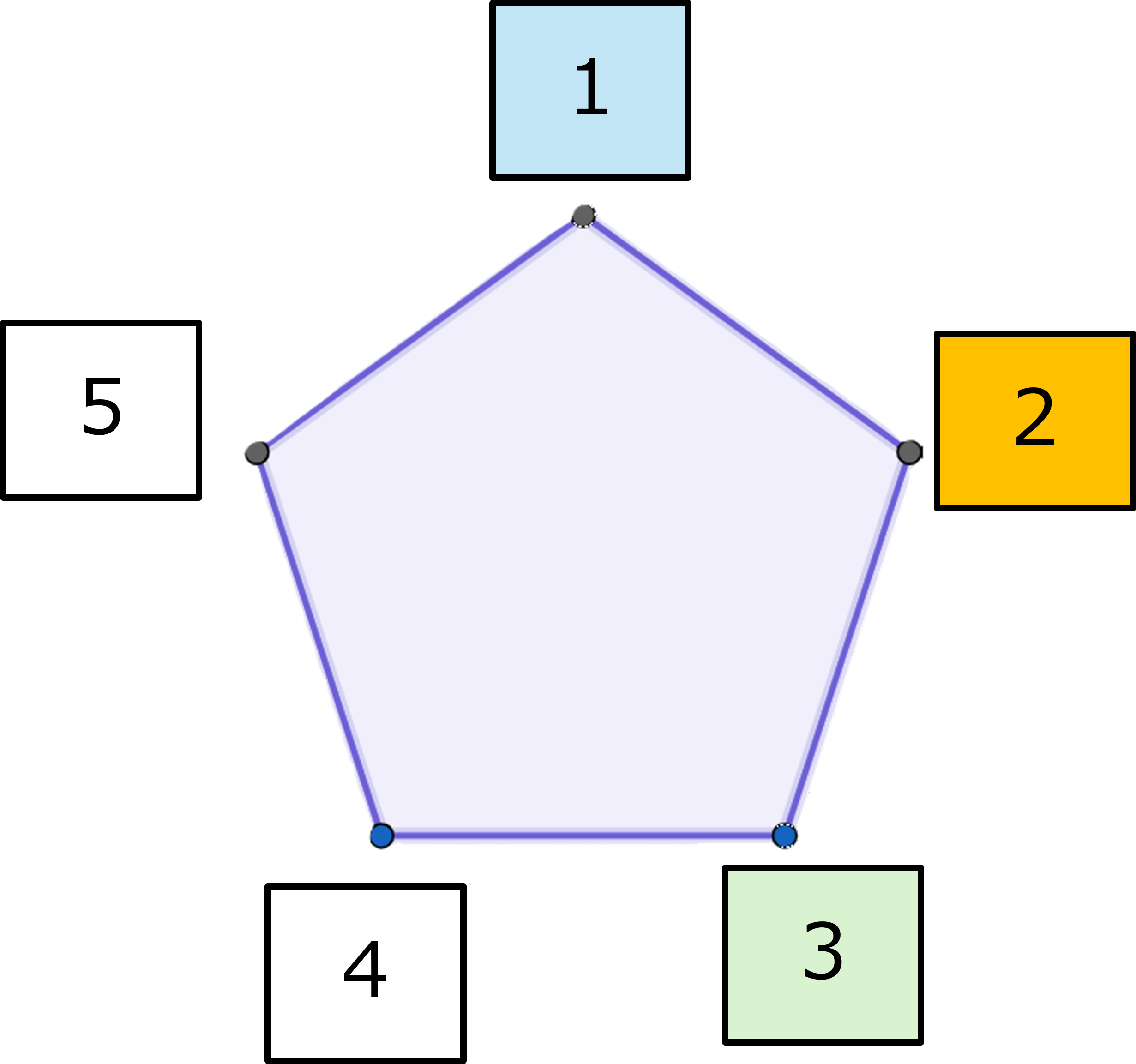 1⊕3=3⊕1=2
1⊕3=3⊕1=2
$1$と$4$については、$5$(そして$5$だけが)が等距離にあるとわかるので
$1 \oplus 4 =4 \oplus 1=5$
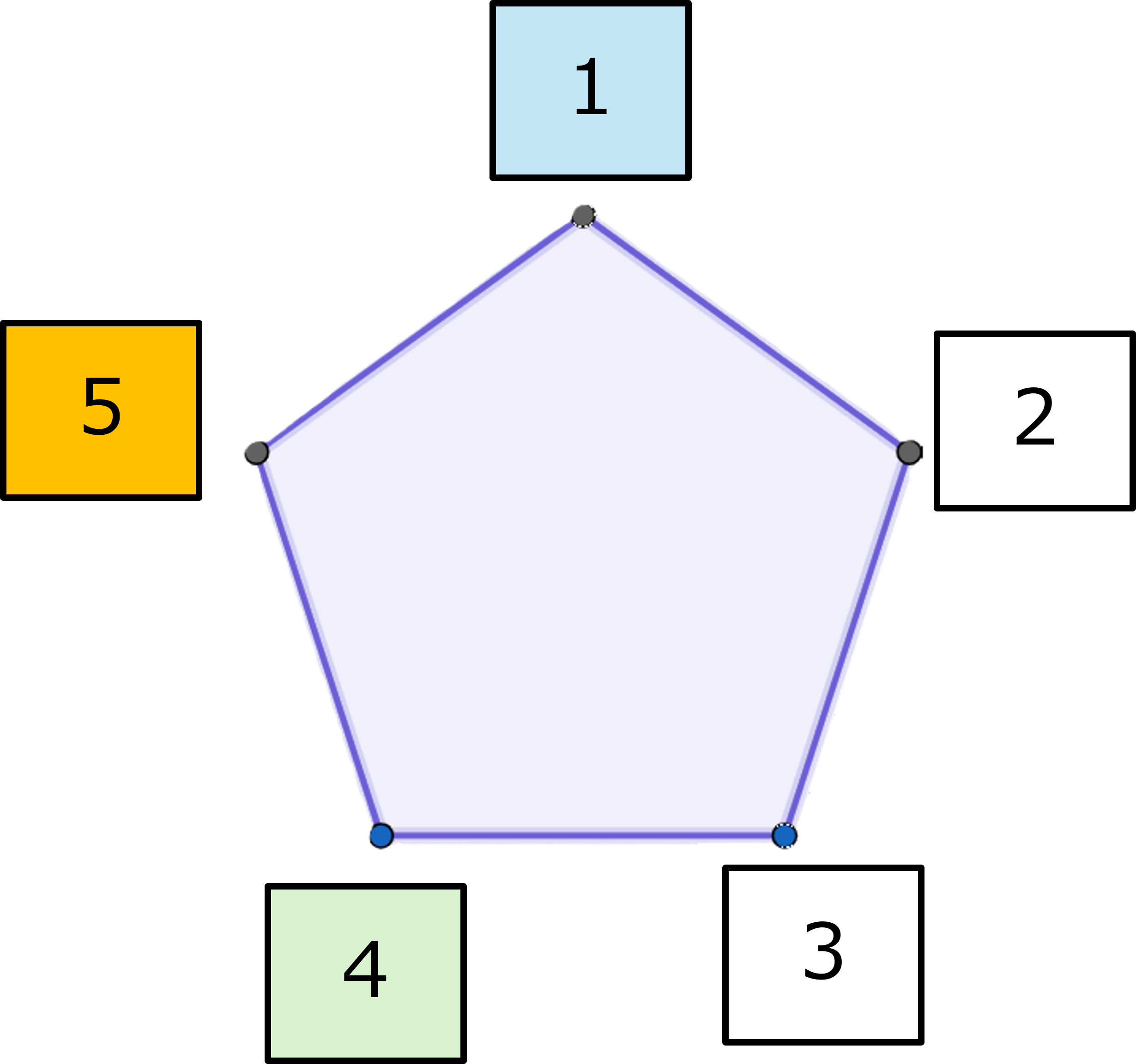 1⊕4=4⊕1=5
1⊕4=4⊕1=5
$1$と$5$については、$3$(そして$3$だけが)が等距離にあるとわかるので
$1 \oplus 5 =5 \oplus 1=3$
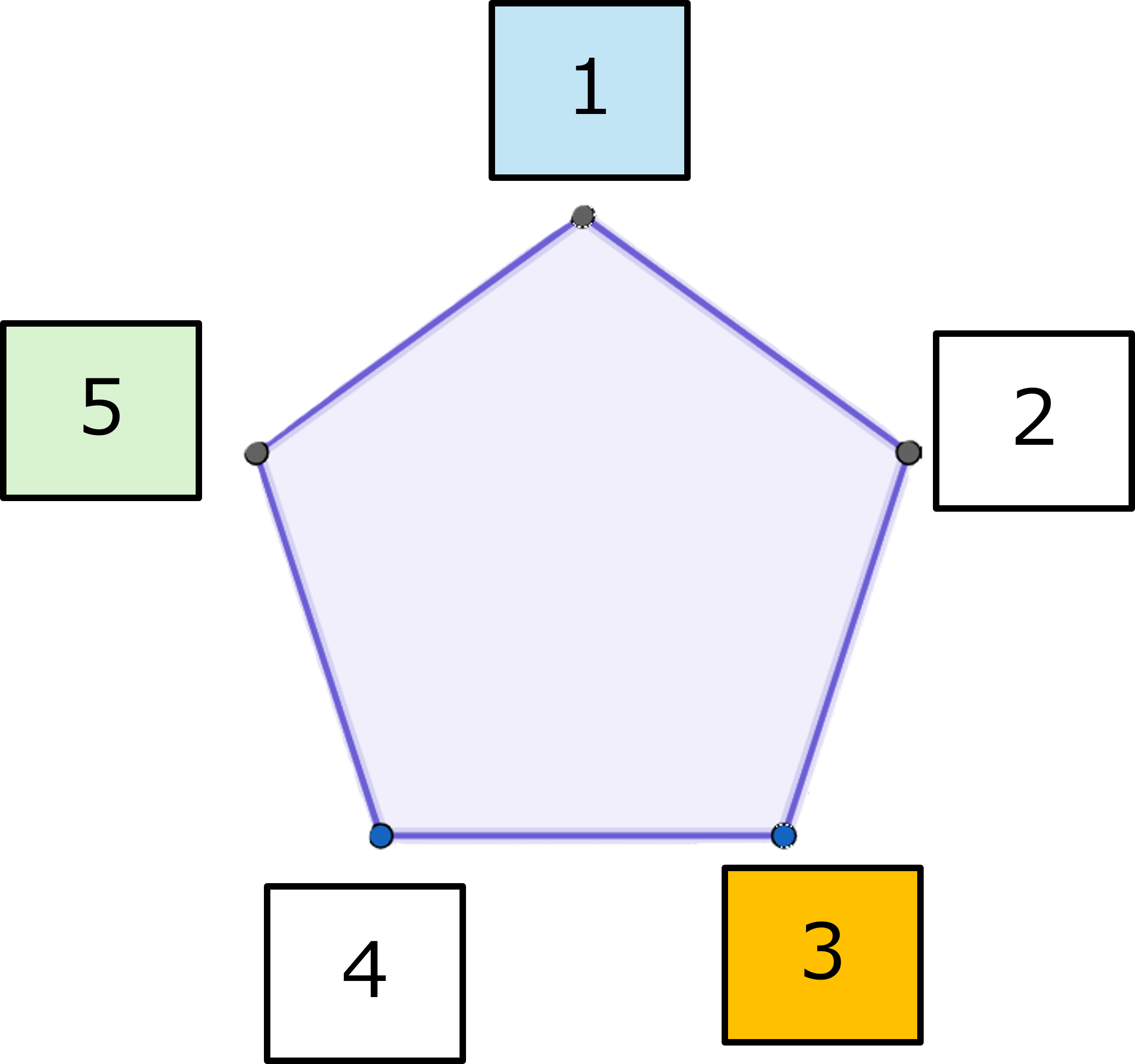 1⊕5=5⊕1=3
1⊕5=5⊕1=3
ここまでで$1→2→3→4→5$のように回せば、他の演算結果も決まるのが分かるが、愚直に確かめる。
$2$と$3$については、$5$(そして$5$だけが)が等距離にあるとわかるので
$2 \oplus 3 =3 \oplus 2=5$
$2$と$4$については、$3$(そして$3$だけが)が等距離にあるとわかるので
$2 \oplus 4 =4 \oplus 2=3$
$2$と$5$については、$1$(そして$1$だけが)が等距離にあるとわかるので
$2 \oplus 5 =5 \oplus 2=1$
$3$と$4$については、$1$(そして$1$だけが)が等距離にあるとわかるので
$3 \oplus 4 =4 \oplus 3=1$
$3$と$5$については、$4$(そして$4$だけが)が等距離にあるとわかるので
$3 \oplus 5 =5 \oplus 3=4$
$4$と$5$については、$2$(そして$2$だけが)が等距離にあるとわかるので
$4 \oplus 5 =5 \oplus 4=2$
乗積表は以下のようになる。
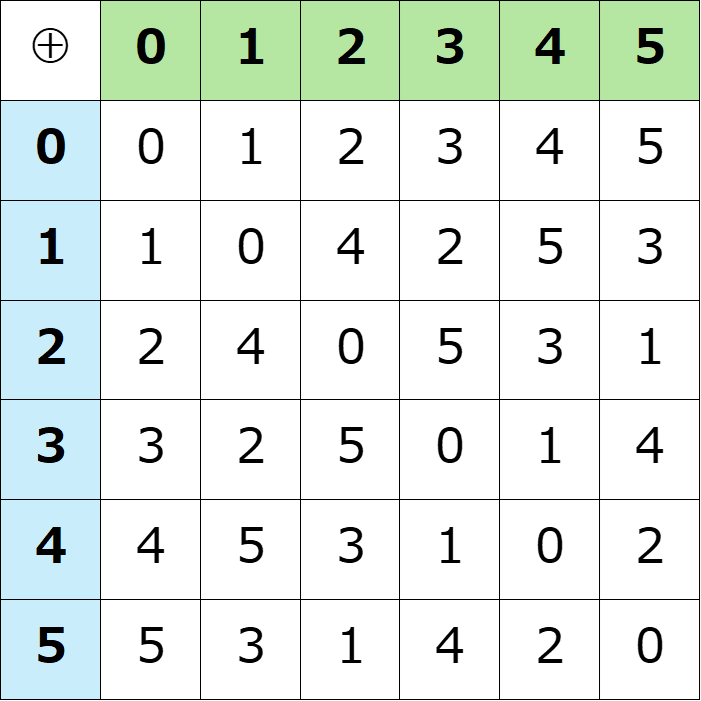 完成した乗積表
完成した乗積表
群の公理を確かめる
- 閉じていること
演算結果も$S=\{0,1,2,3,4,5\}$の元である。閉じている。 - 結合律は成り立たない
$1\oplus (2 \oplus 3)=1 \oplus 5$$=3$
$(1\oplus 2) \oplus 3=4\oplus 3$$=1$
よって結合律は満たさない - 単位元の存在
定義の$x \oplus 0 = 0 \oplus x = x$より$0$が単位元である。 - 逆元の存在
定義の$x \oplus x = 0$より$x$の逆元は$x$である。 - 可換である
定義より$y\oplus x=x\oplus y$
群の公理のうち結合律以外を満たし、さらに可換でもある。しかし、結合律は満たさない。
つまり、$(S,\oplus)$は群ではない。
一見、対称性も高そうな演算なのに、結合律を満たさないのである。
これを正3角形で行ったら
自分が考えた順とは逆になるが、定義の正5角形を正3角形に変えたらどうなるか?
$S=\{0,1,2,3\} $の$2$つの数から、$S$の$1$つの数$x \oplus y $を定める。
$x,y \in S;x \oplus y \in S$
- $0$と他の元$x$の演算結果は$x$とする。
$x \oplus 0 = 0 \oplus x = x$ - $x$と同じ元$x$の演算結果は$0$とする。
$x \oplus x = 0$ - 平面上に正3角形を書いて、頂点に$1,2,3$のラベルを付与する。
$x ,y \in S-\{0\}$に対して、対応する$2$つの頂点から平面上同じ距離にある頂点のラベル$z$で$x\oplus y≝z$と定義する。
$0$でない元の演算は選んだ$2$つ以外の数が結果となる。
$1\oplus 2=3 $
$1\oplus 3=2 $
$2\oplus 3=1$
乗積表は以下のようになる。
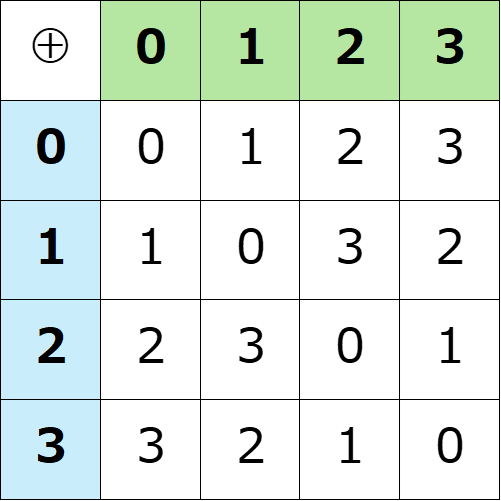 正3角形の頂点の演算の乗積表
正3角形の頂点の演算の乗積表
この演算表は前の記事の最後でXOR演算を元にした演算なす群(結果的にクラインの四元群$\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$と同型)として紹介した$S=\{0,1,2,3\}$のXOR演算を元にした演算の乗積表と一致する。こちらはもちろん、前回の記事で示した通り、群になっている。(結合律は、二進表示したときの各桁の$0,1$のXOR演算の結合律から満たされることがわかる。)
自分はこのクラインの四元群を拡張しようとして今回の6元集合の演算を思いついた。しかしそれは結合律は満たさないものだった。
終わりに
群ではもちろん定義から結合律を満たす。置換群における置換(全単射)の合成演算では結合律は明らかなので、乗積表が与えられたら結合律は「満たされる」と思いがちだが、今回の例のように結合律を「満たさない」例もある。「確かめる」ことの重要性を改めて思い知らされた。
群などの定義や簡単な例さえわかれば、それ以上の深い数学知識は不要で、要素数が少ない集合の演算を色々と考えて、一人遊び的にパズルとして楽しめるという事が分かった。知識の積み上げが必要な数学ももちろんあるが、このように予備知識は少なめでも「知っていることだけ」をオモチャにして楽しむことができるのは数学ならではないかと思う。