【Causality備忘録】Reflecting spacetime
これは私の備忘録なので、まとまってないし読まないほうがいいです。随時加筆します。
reflecting時空についてまとめます。
時空$(M,g)$が点$q\in M$ において過去反射的(past reflecting)であるとは、次の同値な３つの条件を満たすときを言う。
$I^+(p)\supset I^+(q)\ \Rightarrow\ I^-(p)\subset I^-(q)$
$q\in \overline{I^+(p)}\ \Rightarrow\ p\in \overline{I^-(q)}$
$q\in \partial I^+(p)\ \Rightarrow\ p\in \partial I^-(q)$
さらに任意の点が過去反射的であるとき、時空$(M,g)$は過去反射的であるという。未来と過去を入れ替えて未来反射的も同様に定義する。過去反射的かつ未来反射的であるとき、時空$(M,g)$は反射的であるという。
下図はpast reflectingでない時空の例です。
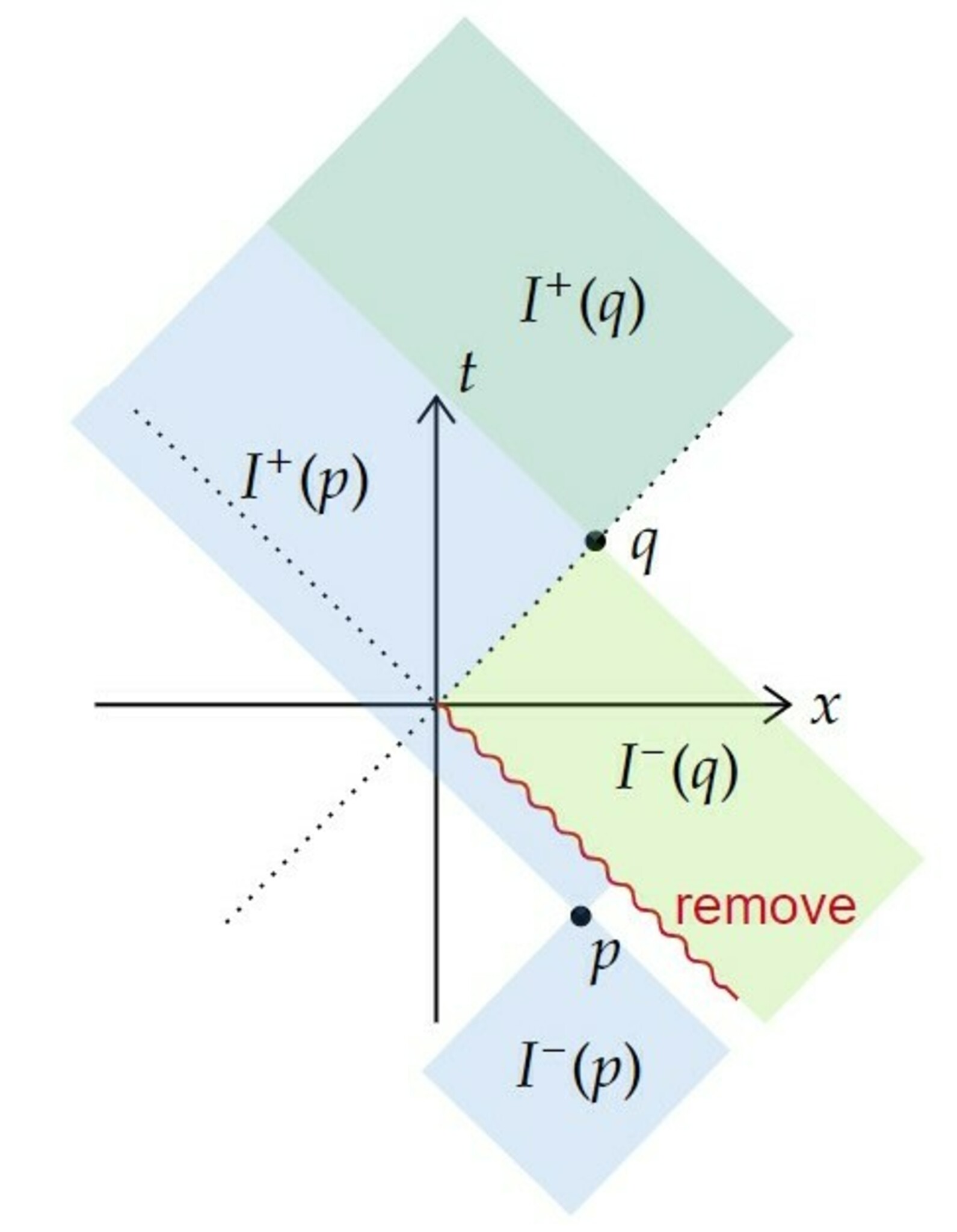past reflectingでない時空
この定義だとreflectingという性質の物理的、幾何学的意味が分かりずらいです。reflectingは時空の因果構造が適当な意味で“連続”であるということと同値です。$I^\pm$の外側連続性、（未来、過去）体積関数の連続性と同値であることが知られています（ https://math.jp/wiki/%E5%9B%A0%E6%9E%9C%E9%9A%8E%E5%B1%A4#.E5.9B.A0.E6.9E.9C.E6.A7.8B.E9.80.A0.E3.81.AE.E9.80.A3.E7.B6.9A.E6.80.A7）。
その他の特徴付けとしてchronological common future(past)による特徴付けを述べます。
$(M,g)$を時空とし、$S\subset M$を部分集合とする。$S$のchronological commom futureを
$$
\uparrow S:={\rm Int}\{x\in M;\ y<< x,\ \forall y\in I^-(S)\}
$$
と定義する。chronological commom past $\downarrow S$も過去、未来を入れ替えて同様に定義する。
$\uparrow S$はだいたい$S$の過去の任意の元が原理的に到達できる未来ということです。同様に、$\downarrow S$はだいたい$S$の未来の任意の元が信号を原理的に受け取ることができる過去ということです。
定義より$ \downarrow I^+(p)\supset I^-(p)$は明らかです。$p$は$I^-(p)$の情報のみ受け取りますが、$ \downarrow I^+(p)$が$I^-(p)$を真に含む場合は$p$の未来のどの点$q\in I^+(p)$も$I^-(p)$の領域外からの情報を受け取るということになります。この状況では$p$を通る観測者が過去から受け取れる情報が$p$を境に激変することを意味しています（信号は壁などの物体で遮蔽されていて、移動したら急にその後ろが見えたという状況ではない、物体で遮蔽されていても原理上透過力の強い粒子で検出できる）。これはいかにも因果構造が“不連続”そうです。従って因果構造が連続であるならば$ \downarrow I^\pm(p)= I^\mp(p)$となるべきです。
Mがreflectingであることと、任意の$p\in M$に対して$ \downarrow I^+(p)=I^-(p),\ \uparrow I^-(p)=I^+(p)$となることは同値である。
Mがreflectingであるとする。
$ \downarrow I^+(p)\subset I^-(p)$を示す。
$ \downarrow I^+(p)$の定義より$ q\in\downarrow I^+(p)$に対して、$ I^+(q)\supset I^+(p)$となる。
よってpast reflectingより$ I^-(q)\subset I^-(p)$となる。$\cdots(*)$
$ \downarrow I^+(p)$はopensetだから、$ q$はある$ q^+\in\downarrow I^+(p)$の過去にある。
$(\ast)$を導いた議論と同様にして$ I^-(q^+)\subset I^-(p)$が分かるから、$q\in I^-(p)$である。$ \downarrow I^+(p)\supset I^-(p)$は定義より明らか。
よって$ \downarrow I^+(p)= I^-(p)$である。future reflectingより$\uparrow I^-(p)=I^+(p)$も同様に従う。
逆に、$ \downarrow I^+(p)= I^-(p),\ \uparrow I^-(p)=I^+(p)$を仮定する。
$ I^+(q)\subset I^+(p)$とすると、$ \downarrow I^+(q)\supset \downarrow I^+(p)$となるから、$ I^-(q)\supset I^-(p)$である。よってpast reflectingである。future reflectingも同様である。
この特徴づけを使うとhomogeneousな時空はreflectingであることが分かります。
homogeneousな時空はreflectingである
$ \uparrow I^-(p)=I^+(p)$のみ示す。
$ \uparrow I^-(p)\subset I^+(p)$を示せばよい。
$ y\in \uparrow I^-(p)$とする。
$ G$が$ M$に推移的に作用するとする。
$ W':=\{g\in G;\ g(y)\in\uparrow I^-(p)\}$ (単位元を含むopenset)
$ W=W'\cap (W')^{-1}$とする。
$ g\in W$に対して、$ g^{-1}(y)\in\uparrow I^-(p)$より$ y\in g(\uparrow I^-(p))$となる。
$ q\in \uparrow I^-(p)$とする。
$ \forall p^-\in I^-(p)$に対して、$ p^-<< p<< q$であるから、$ g(p^-)<< g(p)<< g(q)$である。
$ I^-(g(p))=\{g(p^-);p^-\in I^-(p)\}$だから$ g(q)\in \uparrow I^-(g(p))$である。
よって$ g(\uparrow I^-(p))\subset \uparrow I^-(g(p))$なので$ y\in \uparrow I^-(g(p))$である。
適当な$ g\in W$があって$ p<< g(p)$となるから、$ p<< g(p)<< y$である
よって$ y\in I^+(p)$である。
$ \downarrow I^+(p)=I^-(p)$も同様である。
類似の命題として「定常時空はreflecting」が成り立ちます（ https://mathlog.info/articles/3570 の命題９）。