Fibonacci 平方数が 0, 1, 144 のみであることの初等的証明
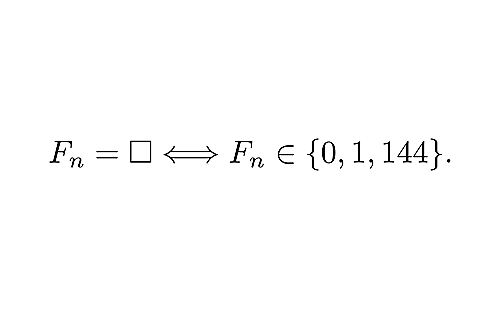黄金平方数
前提知識 : Lucas 数列, Fibonacci 数列, 平方剰余の第一補充則 (Euler の規準)
Lucas 数列, Fibonacci 数列 :
https://mathlog.info/articles/19
Euler の規準 :
https://mathlog.info/articles/454
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
最新版のブログ記事 :
フィボナッチ数列に現れる平方数が 1 と 144 のみであることについて
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
剰余を見る証明
ある整数$N$について, これが平方数であるか否かを表現する方程式,
$$
\begin{align}
m^2=N
\end{align}
$$の解析法には, 周知されているごとく様々な手法が存在するが, ここでは方程式$F_n=m^2$の解を決定するにあたって, ある特殊な整数の素因子と剰余とを観察する. 文字$p$を奇素数とするとき, 合同方程式
$$
\begin{align}
x^2\equiv-1\ \ ({\rm mod}\ p)
\end{align}
$$が可解であるためには, $p\equiv1\ \ ({\rm mod}\ 4)$なることが必要かつ充分である. 故に, 若しある整数$M\equiv3\ \ ({\rm mod}\ 4)$をもって$F_n\equiv-1\ \ ({\rm mod}\ M)$を成立せしめることができるならば, $M$は$4$で割って$3$余る素因子$p$を必ず持ち, $F_n$が平方数に成ることは$F_n≡-1\ \ ({\rm mod}\ p)$の相合によって否定される. $n$にとって必要なる条件が得られるのである.
この概略の妥当性の理解を助けるための実験として, 以下に数列$(F_n+1)_{n>0}$に現れる各項の素因子分解を示す.
$$
\begin{align}
2=&\;2,\\
2=&\;2,\\
3=&\;\textbf{3},\\
4=&\;2^2,\\
6=&\;2\times\textbf{3},\\
9=&\;\textbf{3}^2,\\
14=&\;2\times\textbf{7},\\
35=&\;5\times\textbf{3},\\
56=&\;2^3\times\textbf{7},\\
90=&\;2\times5\times\textbf{3}^2,\\
145=&\;(5\times29),\\
234=&\;2\times13\times\textbf{3}^2,\\
378=&\;2\times(\textbf{3}^3\times\textbf{7}),\\
611=&\;13\times\textbf{47},\\
988=&\;2^2\times13\times\textbf{19},\\
1598=&\;2\times29\times\textbf{31},\\
2585=&\;5\times(\textbf{11}\times\textbf{47}),\\
4182=&\;2\times(17\times41)\times\textbf{3},\\
6766=&\;2\times17\times\textbf{199},\\
10947=&\;(41\times89)\times\textbf{3},\\
17712=&\;2^2\times13\times(\textbf{3}\times\textbf{227}),\\
28658=&\;2\times89\times(\textbf{7}\times\textbf{23}),\\
46389=&\;3\times(\textbf{7}\times\textbf{47}^2),\\
&\vdots
\end{align}
$$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
前置き
任意の$n\in\mathbb{Z}$に対して, $\begin{cases}\displaystyle\phi^n=\frac{L_n+\sqrt{5}F_n}{2}\\\displaystyle\bar{\phi}^n=\frac{L_n-\sqrt{5}F_n}{2}\end{cases}$が成りたつ.
$n=0,1$のときは正しい. それぞれの等式について, ある$n+1,n$について等式が成りたつならば, それらを辺々足しあわせる操作によって$n+2$の場合が得られ. また辺々を引けば$n-1$の場合が得られるので, 再帰的に, 命題の等式が成りたつ. $\quad\Box$
任意の$n\in\mathbb{Z}$に対して, $L_n^2-5F_n^2=4\cdot(-1)^n$が成りたつ.
指数法則$\phi^{n}\bar{\phi}^n=(\phi\bar{\phi})^n$を変形すれば,
$$
\begin{align}
&\phi^{n}\bar{\phi}^n=(\phi\bar{\phi})^n\\
\Longleftrightarrow&\;\frac{L_n+\sqrt{5}F_n}{2}\cdot\frac{L_n-\sqrt{5}F_n}{2}=(-1)^n\\
\Longleftrightarrow&\;L_n^2-5F_n^2=4\cdot(-1)^n
\end{align}
$$の式になる. $\quad\Box$
任意の$n\in\mathbb{Z}$に対して, $\begin{cases} F_{2n}=L_nF_n\\ L_{2n}=L_n^2-2(-1)^n \end{cases}$が成りたつ.
加法定理と先の補題によって,
$$
\begin{align}
2F_{2n}&=L_nF_n+F_nL_n=2L_nF_n,\\
2L_{2n}&=L_nL_n+5F_nF_n\\
&=L_n^2+\left(L_n^2-4(-1)^n\right)\\
&=2L_n^2-4(-1)^n
\end{align}
$$の計算が成りたつ. $\quad\Box$
任意の$n\in\mathbb{Z}$に対して, $2\mid L_n\Longleftrightarrow2\mid F_n\Longleftrightarrow3\mid n$が成りたつ.
数列$(L_n),(F_n)$を${\rm mod}\ 2$によって還元する場合, $0,1,1$の繰りかえす同一の周期列が得られる. 故に補題が成立する. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
法の構成
任意の$m,n\in\mathbb{Z}$に対して, $2\mid n$かつ$3\nmid n$ならば,
$$
\begin{align}
F_{m+2n}&\equiv-F_m\quad({\rm mod}\ L_n)
\end{align}
$$が成りたつ.
加法定理と二倍公式から,
$$
\begin{align}
2F_{m+2n}=&\;L_mF_{2n}+F_mL_{2n}\\
=&\;L_mL_nF_n+F_m(L_n^2-2\cdot(-1)^n)\\
\equiv&\;-2F_m\quad({\rm mod}\ L_n)
\end{align}
$$である. 今$2\nmid L_n$のために, 各辺を$2$により除することができる. ここから補題の式が導かれるのである. 第二式についても全く同じ. $\quad\Box$
上の合同式の右辺は$n$に依存しない数である. 故に, $n$が$3$によって可除である場合にも, 次のように拡張することができる.
任意の$m,n\in\mathbb{Z}$に対して, $2\mid n$ならば,
$$
\begin{align}
F_{m+2n}&\equiv-F_m\quad({\rm mod}\ L_{n'})
\end{align}
$$が成りたつ. ただし, 整数$n'$は$n$が素因子$3$を失ったものである.
$n$から素因子$3$を抽出して,
$$
\begin{align}
n=3^e\cdot n'=n'+n'+\cdots+n'
\end{align}
$$と表せば, 先の補題を$3^e$回繰りかえして, 補題の式を得ることができる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
証明
$n$の取りうる数全体を,
$$
\begin{align}
\mathbb{Z}=(4\mathbb{Z}+1)\cup(4\mathbb{Z}+3)\cup2\mathbb{Z}
\end{align}
$$と分割して, 場合を三つに分ける.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$n\equiv1\ \ ({\rm mod}\ 4)$のとき
任意の$n\in\mathbb{Z}$に対して, $n\equiv1\ \ ({\rm mod}\ 4)$ならば, $F_n\in\Box\Longrightarrow n=1$が成りたつ.
$n=1+2k$なる非零偶数$k$を取り, $k=3^e\cdot k'$として素因子$3$を抽出すれば,
$$
\begin{align}
F_n=F_{1+2k}\equiv-1\ \ ({\rm mod}\ L_{k'})
\end{align}
$$を得る. $k'\ {\rm mod}\ 6\in\{2,4\}$により$L_{k'}\equiv3\ \ ({\rm mod}\ 4)$であるから, $F_n$は$L_{k'}$を法として平方非剰余である. $\quad\Box$
剰余列$(L_n\ {\rm mod}\ 4)$は節$2,1,3,0,3,3$の成す周期列である.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$n\equiv3\ \ ({\rm mod}\ 4)$のとき
任意の$n\in\mathbb{Z}$に対して, $n\equiv3\ \ ({\rm mod}\ 4)$ならば, $F_n\in\Box\Longrightarrow n=-1$が成りたつ.
$F_n$と$F_{-n}$は相等しい. 由って, $n\equiv1\ \ ({\rm mod}\ 4)$の場合を考えて, $n$を$-n$に擦りかえれ命題が得られる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$n\equiv0\ \ ({\rm mod}\ 2)$のとき
前記の場合と同様に考えることはできない. 二倍公式
$$
\begin{align}
F_{n}=L_{n/2}F_{n/2}
\end{align}
$$によって$F_n$を因数に分解するとき, 等式$|L_{n/2}^2-5F_{n/2}^2|=4$のために, $(L_{n/2}$と$F_{n/2})$の最大公約は$1$と$2$に限られる. 従って, $F_{n/2}$と$2F_{n/2}$の内何れかが平方数でなければならない. この推論を繰りかえせば, 終には奇数$n$であって, $F_n$または$2F_n$が平方数に成る数を決定するところにまで問題が帰結する. 実際の証明においては, $n$が$2$により割りきれる回数を変量として, これに関する数学的帰納法を適用し, 逆流するように論証をすればよろしい.
任意の$n\in\mathbb{Z}$に対して, $n\equiv3\ \ ({\rm mod}\ 4)$ならば, $2F_n\in\Box\Longrightarrow n=3$が成りたつ.
$n=3+2k$なる非零偶数$k$を取り, $k=3^e\cdot k'$として素因子$3$を抽出すれば,
$$
\begin{align}
2F_n=2F_{3+2k}\equiv-1\cdot2^2\ \ ({\rm mod}\ L_{k'})
\end{align}
$$を得る. $k'\ {\rm mod}\ 6\in\{2,4\}$により$L_{k'}\equiv3\ \ ({\rm mod}\ 4)$であるので, $F_n$は$L_{k'}$を法として平方非剰余である. $\quad\Box$
任意の$n\in\mathbb{Z}$に対して, $n\equiv1\ \ ({\rm mod}\ 4)$ならば, $2F_n\in\Box\Longrightarrow n=-3$が成りたつ.
$F_n$と$F_{-n}$は相等しい. 由って, $n\equiv3\ \ ({\rm mod}\ 4)$の場合を考えて, $n$を$-n$に擦りかえれはこの命題が得られる. $\quad\Box$
任意の$n\in2\mathbb{Z}$に対して, $(F_n\in\Box)\vee(2F_n\in\Box)\Longleftrightarrow n\in\{0,2,6,12\}$が成りたつ.
論を簡潔にするために, 整数の部分集合として,
$$
\begin{align}
S=\{n^2\mid n\in\mathbb{Z}\}\cup\{2n^2\mid n\in\mathbb{Z}\}
\end{align}
$$を定義する.
$n=0$について示すべきことは無い. $n\neq0$であるとき, $n=2^e\cdot f$として素因子$2$を抽出し, $e\geqslant3$を充たすあらゆる$F_n$が$S$の要素でないことを, 帰納的に論ずる.
$(1)\quad$$e=1$のとき
$F_n=L_fF_f$において, $F_f\in S$でなければならないから, これまでの証明によって$n\in\{-6,-2,2,6\}$が要求される. この内$2$と$6$のみが充分性を充たす.
$(2)\quad$$e=2$のとき
$F_n=L_{2f}F_{2f}$において, $F_{2f}\in S$でなければならないから, $(1)$の証明によって$n\in\{4,12\}$が要求される. この内$12$のみが充分性を充たす.
$(3)\quad$$e=3$のとき
$F_n=L_{4f}F_{4f}$において, $F_{4f}\in S$なければならないから, $(3)$の証明によって$n=24$が要求される. けれどもこれは充分性を充たさない.
$(4)\quad$$e\geqslant4$のとき
$e-1$に関して, $F_{2^{e-1}f}$が如何なる$f$においても$S$の要素に成らないことを仮定とする. そのとき, $F_{2^ef}\in S$に成るためには, $F_{2^ef}=L_{2^{e-1}f}F_{2^{e-1}f}$の式において, $F_{2^{e-1}f}\in S$でなければならないが, 仮定によってこれは不可能である. $e=3$のとき, 既に$n$は存在しない. この結果はあらゆる$e\geqslant4$についても同じである. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
結論
以上によって次の定理の証明が完成する.
数列$(F_n)_{n\in\mathbb{Z}}$に現れる平方数は$0,1,144$のみである.
数列$(F_n)_{n\in\mathbb{Z}}$に現れる平方数の二倍は$0,2,8$のみである.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
この記事を高評価した人
この記事に送られたバッジ
投稿者
