複素解析：解析接続
今回の目標
今回の記事では、正則関数の解析接続を紹介します。解析接続にもいろいろな種類があると思いますが、今回は領域から別の領域への解析接続という形で紹介したいと思います。
今回の予備知識
用語について
- 連結な開集合を領域といいます。
定義・定理について
複素数の意味で微分可能な関数のことを正則関数と呼びます：
$\Omega \subset \mathbb{C}$を領域とする。関数$f: \Omega \to \mathbb{C}$が正則であるとは、任意の$z \in \Omega$に対して、極限$$\lim_{h \to 0}\frac{f(z+h) - f(z)}{h} $$が存在することをいう。
正則関数に対して、一致の定理と呼ばれる定理が成り立ちます：
$\Omega \subset \mathbb{C}$を領域とし、$f, g: \Omega \to \mathbb{C}$を正則関数とする。$\Omega$内の点列$\{z_j\}_{j \in \mathbb{N}}$と$z \in \Omega$が存在して、
- $\lim_{j \to +\infty} z_j = z$
- 任意の$j$に対して、$f(z_j) = g(z_j)$
をみたすとする。このとき、任意の$z \in \Omega$に対して$f(z) = g(z)$が成り立つ。
これにより特に、ある(空でない)開集合$U \subset \Omega$が存在して$U$上で$f = g$が成り立つとき、$\Omega$上全体で$f = g$が成り立つことが分かります。
一致の定理については、前回の記事( 複素解析：一致の定理 )も参照ください。
解析接続
今回は、次の意味の解析接続を考えます：
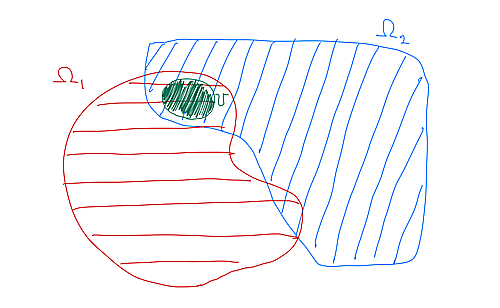
$\Omega_1, \Omega_2 \subset\mathbb{C}$を領域とし、$U \subset \Omega_1 \cap \Omega_2$を空でない領域とする。$f_1 : \Omega_1 \to \mathbb{C}$, $f_2 : \Omega_2 \to \mathbb{C}$を正則関数とする。$f_2$が$U$をのりしろとした$f_1$の$\Omega_2$への解析接続であるとは、$U$上で$f_1 = f_2$が成り立つことをいう。
状況を絵で描くとこんな感じになります ↓
図でいう左側の領域$\Omega_1$上の正則関数$f_1$を、真ん中の$U$という部分を介して右側の$\Omega_2$上まで「広げる」わけですね。$U$で関数を貼り付ける感覚を今回は「のりしろ」と表現してみました。
いくつか気を付けるところがありますので、順に見ていきましょう。
- $U$をのりしろとした$f_1$の$\Omega_2$への解析接続は、存在すればただひとつであることが分かります。
実際、ふたつ存在したとすると、それらは$U$上で一致するので、一致の定理から$\Omega_2$全体でも一致しています。 - 例えば上の絵では$\Omega_1$と$\Omega_2$の共通部分$\Omega_1 \cap \Omega_2$は上下ふたつの連結成分をもちますが、$U$をのりしろとした解析接続の場合、$f_1 = f_2$となることが保証されているのは上側の$U$を含む連結成分だけになります。下側の連結成分では$f_1$と$f_2$は一致するかもしれませんし、一致しないかもしれません。
- 一致しない場合、$\Omega_1$と$\Omega_2$の間にある「穴」の周りをぐるっとたどって関数をつなげていくと、別の関数になっているということになります。このような例は今後解析接続の例として紹介するかもしれません。
はじめての解析接続
それでは、簡単ですが上の定義に従った解析接続の例を紹介してみます。
べき級数で定義された関数
$$f(z) = 1 + z + z^2 + \cdots + z^n + \cdots$$
を考えます。このべき級数は収束半径が$1$なので、原点を中心とした半径1の円の内部$\Delta$で収束し、その上の正則関数を定めます。
一方、$z \in \Delta$のとき、
\begin{align*}
f(z)(1-z) &= \lim_{n \to +\infty} (1 + z + \cdots + z^n)(1-z)\\
& = \lim_{n \to +\infty}(1-z^{n+1})\\
& = 1
\end{align*}
ですから、$z \in \Delta$に対して、
$$f(z) = \frac{1}{1-z}$$
が成り立つことが分かります。すると、右辺は、$\mathbb{C} \setminus \{1\}$上の正則関数になっています。
以上により、$\displaystyle\frac{1}{1-z}$は$\Delta$をのりしろとした$f(z)$の$\mathbb{C} \setminus \{1\}$への解析接続であることが分かりました。$f(z)$を定義したときのべき級数の形では、$\Delta$の外側では定義できていないことに注意してください。このように、べき級数を変形して定義域を広げることも立派な解析接続です。
次回はまた別の解析接続の例を紹介したいと思います。それではまた！