拘束系における汎関数の極小化とNewton法

【更新履歴】

• 31Jan.2024: 「公式2」およびその説明に関し軽微な修正を行いました

はじめに

微分方程式を数値的に解く方法のひとつにgradient flowと呼ばれるものがあります。これは作用汎関数やエネルギー汎関数において、配位を勾配のマイナスの方向に数値的にフローさせて極小化することで微分方程式の解を求める方法です。様々な場面で使えると思いますが、例えば場の理論におけるトポロジカルで静的な解を求める際には大変有用ですManton。

このような数値的な汎関数の極小化において拘束条件を課さなければならないことがあります。簡単な例が懸垂線です。懸垂線はひもを垂らしたときの形であり、重力下におけるひものエネルギーの極小化により導けます。しかし数値計算ではひもの長さを固定しないと望まない方向に配位がフローしてしまいます。

本記事では拘束の存在する汎関数の極小化問題をLagrangeの未定乗数法とNewton法により解く方法に関して記します。そして具体的に数値計算で懸垂線を求めます。

本記事では主にWashioを参考にしました。またLagrangeの未定乗数法は既知として、Newton法および2つの方法の融合に焦点を当てます。未定乗数法に関しては例えばLagrangeをご参照ください。

Newton法

Newton法 (Newton-Raphson法) とは方程式の解を求めるための方法ですHayakawa。いま
\begin{align} f_l(u_1,\ldots,u_n)=0 \ \ \ \ (l=1,\ldots, n) \end{align}
の解を近似的に求めることにします。そのためにまず$P^0: (u^0_1,u_2^0,\ldots,u_n^0)$を適当に選びます。$f_l$の値を$z$方向として、$z=f_l(u_1,\ldots,u_n)$の$P^0$における接超平面の$z=0$での$u_i$の値で解を近似するのがNewton法です。方程式が$n$個あれば$u_1,\ldots,u_n$が一意に定まります。

以下これを図を用いて説明します。

1次元の場合

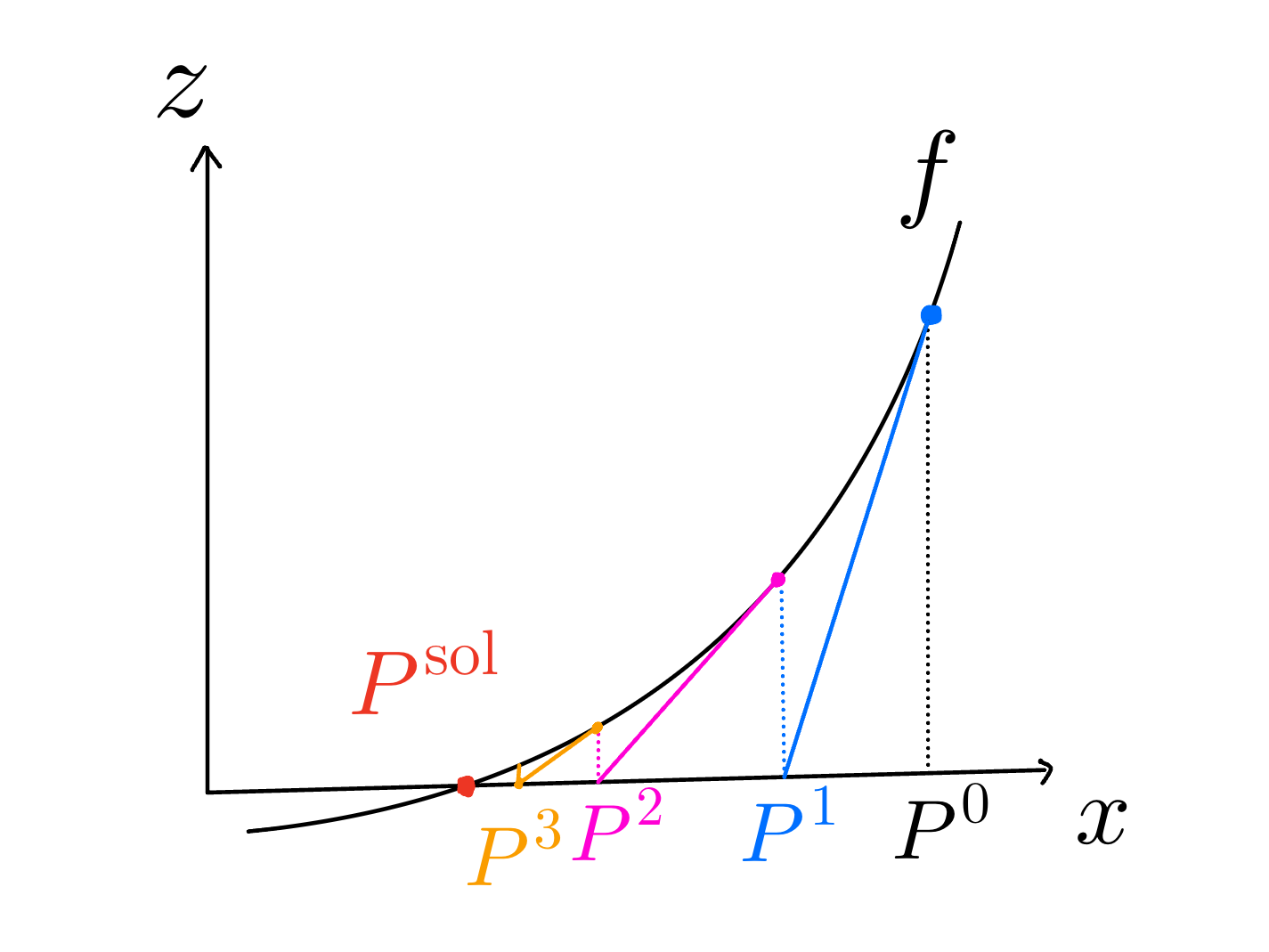1次元のNewton法の概念図

一次元の場合のNewton法が図1です。 最初に$P^0$を適当に選びます。$P^0$における$z=f(x)$の接線が$z=0$と交わる点を$P^1$とします。これを繰り返し$P^2,P^3,\ldots$と続けると、良い初期値$P^0$を選んでおけば真の解$P^\textrm{sol}$に近づきます。

これを具体的に式にするのは簡単です。図1より$P^0: x^0$と$P^1: x^1$との関係が以下になるのはすぐにわかると思います：
\begin{align} f'(x^0)(x^1-x^0)=-f(x^0) \end{align}
この関係は任意の$P^k$と$P^{k+1}$（$k=0,1,2,\ldots$）で成立します。

多次元の場合

2次元のNewton法の概念図。青バツと緑バツがそれぞれ$f,g$の$P^0$における値。バツ印における接平面がそれぞれ$T_f,T_g$。$T_f,T_g$が交わる点が近似解$P^1$。赤点は正しい解。

2次元の場合が図2です。2つの拘束条件が存在するとして、それらを
\begin{align} f(x,y)=0 \ (\textrm{図の青線}), \ \ \ \ g(x,y)=0 \ (\textrm{図の緑線}) \end{align}
とします。まず$P^0:(x^0,y^0)$を適当に選び、$P^0$における$z=f$の接平面$T_f$が$z=0$と交わる線を$f(x,y)=0$の近似解とします。同様に$P^0$における$z=g$の接平面$T_g$が$z=0$と交わる線を$g(x,y)=0$の近似解とします。これらが交わる点$P^1$（オレンジ色の点）が$f=0, g=0$の近似解です。これを繰り返して$P^2,P^3\ldots$と続ければ、良い初期条件の場合真の解$P^\textrm{sol}$（赤点）に近づきます。

この議論を多変数に拡張し式にします。改めて以下の拘束を解くことを考えます:
\begin{align} f_l(u_1,\ldots,u_n)=0 \ \ \ \ (l=1,\ldots, n) \end{align}
$f_l$の高さを$z$とします。ここで
\begin{align} F_l(u_1,\ldots,u_n,z):=f_l(u_1,\ldots,u_n)-z \end{align}
を定義すれば、ある$l$に対する拘束条件$F_l=0$が定める$n$次元超曲面は
\begin{align} z=f_l(u_1,\ldots,u_n)\leftrightarrow F_l(u_l,\ldots,)=0 \end{align}
で表されます。$(n+1)$次元中の点$\tilde P^0:(u^0_1,\ldots,u^0_n,z=f_l(u_1^0,\ldots,u_n^0))$における超曲面$F_l=0$の超接平面を考えます。この平面上の点$(u_1,\ldots,u_n,z)$は以下を満たします：
\begin{align} \left.\sum_{i=0}^n\frac{\partial F_l}{\partial u_i}\right|_{\boldsymbol{u}^0}(u_i-u^0_i)+\frac{\partial F_l}{\partial z}(z-f_l(u_1^0,\ldots,u_n^0))=0 \end{align}
これが成立するのは、$F_l$の勾配が接超平面の法線ベクトルであり、また$(u_1-u^0_1,\ldots,u_n-u^0_n,z-f_l(u_1^0,\ldots,u_n^0))$が接超平面上のベクトルであるため、これら2つのベクトルが直交することに拠ります。この超平面が$z=0$と交わる点の集合（つまり$\tilde P^0$を初期値としたときの近似解）を$u^1_i$とします。$\Delta u_i:=u^1_i-u^0_i$を定義すれば
\begin{align} \left.\sum_{i=0}^n\frac{\partial F_l}{\partial u_i}\right|_{\boldsymbol{u}^0}\Delta u_i+f_l(u_1^0,\ldots,u_n^0)=0 \tag{1}\label{eq1} \end{align}
が成立します。

Eq.(1)を$f$で書き直し、さらに行列表記にしましょう。Jacobian $J_{P^0}$を以下で定義します：
\begin{align} J_{P^0}:= \begin{pmatrix} \frac{\partial f_1}{\partial u_1} & \frac{\partial f_1}{\partial u_2} & \cdots & \frac{\partial f_1}{\partial u_n}\\ \frac{\partial f_2}{\partial u_1} & \frac{\partial f_2}{\partial u_2} & \cdots & \frac{\partial f_2}{\partial u_n}\\ \vdots &\vdots & & \vdots\\ \frac{\partial f_n}{\partial u_1} & \frac{\partial f_n}{\partial u_2} & \cdots & \frac{\partial f_n}{\partial u_n} \end{pmatrix}_{P_0} \end{align}
$P^0$の添字はどの要素も$P^0$における値で評価していることを表しています。$\Delta \boldsymbol{u}$を
\begin{align} \Delta \boldsymbol{u}:=\boldsymbol{u}^1-\boldsymbol{u}^0, \ \ \ \boldsymbol{u}^0:= \begin{pmatrix} u^0_1\\ u^0_2\\ \vdots\\ u^0_n \end{pmatrix} , \ \ \ \boldsymbol{u}^1:= \begin{pmatrix} u^1_1\\ u^1_2\\ \vdots\\ u^1_n \end{pmatrix} \end{align}
とします。すなわち$\boldsymbol{u}^0$は$P^0$の座標値、$\boldsymbol{u}^1$は$P^1$の座標値です。さらに
\begin{align} \boldsymbol{f}_{P^0}:= \begin{pmatrix} f_1\\ f_2\\ \vdots\\ f_n \end{pmatrix}_{P^0} \end{align}
とします。このときEq.(1)は行列表記で以下のように書けます：

各行が$f_l$の各$l \ (1\le l\le n)$に関する近似解を表しており、それらの連立方程式になっています。これを解くには$J_{P^0}^{-1}$を求めて両辺左からかければよいです。これにより
\begin{align} \boldsymbol{u}^1=\boldsymbol{u}^0-J^{-1}_{P^0}\boldsymbol{f}_{P^0} \end{align}
のように次の解の候補を作ることができます。この関係はもちろん任意の$P^k$と$P^{k+1}$（$k=0,1,2,\ldots$）で成立します。

Newton法とLagrangeの未定乗数法

Newton法を拘束条件付き多変数関数の極小化に適用します。以下Ref.Washioを参考にしています。

次の拘束条件付きの最小化問題:
\begin{align} \min_{{\boldsymbol{u}}} f(\boldsymbol{u}),\ \ \ \varphi_l(\boldsymbol{u})=0 \ \ \ (l=1,\ldots,m) \end{align}
を考えます。$\boldsymbol{u}$は$n$次元ベクトルとします。前章では$f$が拘束を表す関数でしたが、以下では$\varphi$が拘束を表し$f$は極小化する対象の関数であることに注意してください。

Lagrangeの未定乗数法に従い
\begin{align} \tilde f({\boldsymbol{u}},\boldsymbol{\lambda}):=f(\boldsymbol{u})+\sum_{l=1}^m\lambda_l\varphi_l(\boldsymbol{u}) \end{align}
を導入します。$\boldsymbol{\lambda}$は$m$次元ベクトルです。そして極小化条件
\begin{align} &\hspace{5.5cm}\frac{\partial \tilde f}{\partial{\boldsymbol{u}}}={\boldsymbol{0}}, \ \ \ \frac{\partial\tilde f}{\partial \boldsymbol\lambda}=\boldsymbol{0}\\ {}\\ &\left(\frac{\partial\tilde f}{\partial \boldsymbol{u}},\frac{\partial\tilde f}{\partial \boldsymbol{\lambda}}\text{はそれぞれ}\frac{\partial\tilde f}{\partial u_i},\frac{\partial\tilde f}{\partial \lambda_l}(i=1,\ldots,n; \ l=1,\ldots,m)\text{のなすベクトルを表す}\right) \end{align}
を前章のNewton法に従い解くことを考えます。ここで$F_k\ (k=1,\ldots,n,n+1,\ldots,n+m)$を
\begin{align} F_k:= \begin{cases} \displaystyle \frac{\partial \tilde f}{\partial u_k}-z & (k=1,\ldots,n)\\ \displaystyle \frac{\partial \tilde f}{\partial \lambda_k}-z & (k=n+1,\ldots,n+m)\\ \end{cases} \end{align}
とします。また
\begin{align} \tilde{\boldsymbol{u}}:= \begin{pmatrix} u_1 \\ \vdots \\ u_n \\ \lambda_1\\ \vdots \\ \lambda_m \end{pmatrix} \end{align}
を導入します。前章の議論に従い$F_k(u_1,\ldots,u_n,\lambda,z)=0$の解をNewton法で求めます。$\tilde P^0$を
\begin{align} \tilde P^0:(u_1^0,\ldots,u_n^0,\lambda_1^0,\ldots,\lambda_m^0,z=\partial \tilde f/\partial \tilde{u}_k) \end{align}
とすると、$\tilde P^0$における$F_k=0$の接超平面は、$(u_1^1,\ldots,u_n^1,\lambda_1^1,\ldots,\lambda_n^1,z)$をこの接平面上の点とし、また$\Delta\tilde {\boldsymbol{u}}:=\tilde{\boldsymbol{u}}^1-\tilde{\boldsymbol{u}}^0$として
\begin{align} \frac{\partial F_k}{\partial\tilde{\boldsymbol{u}}}\cdot \Delta\tilde{\boldsymbol{u}} +\frac{\partial F_k}{\partial z}\left(z-\frac{\partial\tilde f}{\partial\tilde{{u}}_k}\right)=0 \end{align}
で表されます。よってこれが$z=0$と交わるとき$\Delta\tilde{\boldsymbol{u}}$は
\begin{align} \frac{\partial F_k}{\partial \tilde{\boldsymbol{u}}}\cdot\Delta\tilde{\boldsymbol{u}} =-\frac{\partial \tilde f}{\partial\tilde{{u}}_k} \end{align}
を満たします。これを$k=1,\ldots,n$と$n+1,\ldots,m$にわけて書き直します：

• $k=1,\ldots,n$のとき
  \begin{align} \frac{\partial^2 \tilde f}{\partial u_i \partial u_j}\Delta u_j +\frac{\partial^2\tilde f}{\partial u_i\partial\lambda_l}\Delta\lambda_l = -\frac{\partial}{\partial u_i}(f+\lambda_l\varphi_l)\\ \leftrightarrow \underline{\left(\frac{\partial^2 f}{\partial u_i\partial u_j} +\lambda_l\frac{\partial^2 \varphi_l}{\partial u_i\partial u_j}\right)\Delta u_j +\frac{\partial \varphi_l}{\partial u_k}\Delta\lambda_l = -\frac{\partial}{\partial u_i}(f+\lambda_l\varphi_l)} \end{align}
• $n+1,\ldots,m$のとき
  \begin{align} \frac{\partial}{\partial \tilde u_k}\left(\frac{\partial\tilde f}{\partial\lambda_l}\right) \Delta \tilde u_k=-\frac{\partial\tilde f}{\partial\lambda_l} \\ \leftrightarrow \underline{\frac{\partial\varphi_l}{\partial u_i}\Delta u_i=-\varphi_l} \end{align}

ここで繰り返し登場する添字は和を取るものとします。また$i,j$は$1,\ldots,n$、$l$は$1,\ldots,m$、$k$は$1,\ldots,n+m$まで走るものとします。

上の下線を引いた2式を数値計算で扱いやすいように行列表記すれば以下のようになりますWashio：

公式2を$(\Delta\boldsymbol{u},\Delta\boldsymbol{\lambda})$に関して解いて
\begin{align} \begin{pmatrix} \boldsymbol{u}^1\\ \boldsymbol{\lambda}^1 \end{pmatrix} = \begin{pmatrix} \boldsymbol{u}^0\\ \boldsymbol{\lambda}^0 \end{pmatrix} +\begin{pmatrix} \boldsymbol{A} & \boldsymbol{B}\\ \boldsymbol{B}^T & \boldsymbol{0} \end{pmatrix}^{-1} \begin{pmatrix} \boldsymbol{r}_u \\ \boldsymbol{r}_\lambda \end{pmatrix} \end{align}
を計算すれば次の解が求まります。$\boldsymbol{r}_u,\boldsymbol{r}_\lambda$のノルムは収束の指標であり、これがゼロになるとフローは止まり真の解付近に到達します。

具体的な数値計算

2変数関数の拘束付き極小化

まずは2変数関数の拘束付き極値問題を前章の式を用いて数値的に解いてみます。問題はRef.Problemからお借りしました。

解析的な計算はProblemを御覧ください。非自明な極値は
\begin{align} (x,y)=(1/2,1/\sqrt[3]{4}) \end{align}
です。一方初期条件$(x^0,y^0,\lambda^0)=(2,3,4)$から公式2を用いて数値的に計算すると
\begin{array}{ccc} \text{iteration} & x &y &\lambda \\ \hline 0&2.0&3.0&4.0\\ 1 & 0.54621849 & 1.93277311 & 3.134453781512605\\ 2 & 0.33770424 & 1.2948121 & 2.409061718243684\\ 3 & 0.34496225 & 0.88685724 & 1.8879026769714216\\ \vdots & \vdots & \vdots &\vdots\\ 8 & 0.5 & 0.62996052 & 0.9999999999247514\\ 9 & 0.5 & 0.62996052 & 1.0 \end{array}
となります。iterationとは公式2を何回繰り返したかを表す数字です。iterationが9回で本計算の計算精度の範囲において収束します。$1/\sqrt[3]{4}=0.62996052...$であり計算は正しいです。$\lambda=1$も正しい値です。

懸垂線の計算

次にエネルギーの極小化により懸垂線を数値的に求めます。この場合の拘束条件はひもの長さを固定することに対応します。

懸垂線と拘束条件つき変分法

まず懸垂線における変分法について述べます。詳細は省いて説明するので、馴染みのない方は例えばCatenaryをご参照ください。

$x\text{-}y$座標において懸垂線を$u(x)$で表します。このとき極小化したい$u$の汎関数であるエネルギー$f(u)$は
\begin{align} f(u):=\rho g\int_{x_0}^{x_1} dx\ u(x)\sqrt{1+u'^2(x)} \end{align}
ですCatenary。$\rho,g$はそれぞれひもの線密度と重力加速度です。ここでは簡単のため$\rho g=1$とします。拘束条件はひもの長さを$L$に固定する条件であり
\begin{align} \int_{x_0}^{x_1}dx \sqrt{1+u'^2(x)}=L \end{align}
で与えられます。Lagrangeの未定乗数法を用いて拘束条件付きの変分問題を解きます。それには$\tilde f$を
\begin{align} \tilde f(u;\lambda):=\int_{x_0}^{x_1}dx u(x)\sqrt{1+u'^2(x)} -\lambda\left(\int_{x_0}^{x_1}dx\sqrt{1+u'^2(x)}-L \right) \end{align}
で定義し、これが$\delta y$と$\delta \lambda$の変分($\lambda$に関しては微分)がゼロとなる条件を解けばよいです。

数値計算を行うため空間を離散化します。空間を$N-1$等分し、$u$を$u_i \ (i=0,\ldots,N-1)$とします。こうすれば上記変分は変数$u_0,u_1,\ldots,u_{N-1},\lambda$の多変数関数$f(u_0,u_1,\ldots,u_{N-1},\lambda)$の極小化と等価です。以下の量を導入します：
\begin{align} \boldsymbol{u}= \begin{pmatrix} u_0\\ u_1\\ \vdots\\ u_{N-1} \end{pmatrix} ,\ \ \ f(\boldsymbol{u}):=\Delta x\sum_{i=0}^{N-2} (u_i-\lambda)\sqrt{1+\left(\frac{u_{i+1}-u_{i-1}}{2\Delta x}\right)^2} , \ \ \ \varphi(\boldsymbol{u}):=\Delta x\sum_{i=0}^{N-2} \sqrt{1+u_i^2}-L \end{align}
$f$は極小化する目的関数、$\varphi$は拘束条件、$\Delta x$は最近接の2点の間隔です。計算に関係ない$f$の定数項は落としました。この表式では微分に関して$\Delta x$の2次の精度である一方、積分に関して0次なのですが、これで議論を進めます。

あとは$\partial f/\partial\boldsymbol{u},\partial^2 f/\partial \boldsymbol{u}^2$（および$f\to\varphi$とした量）を上の表式を用いて構成し、公式2を繰り返し計算すればよいです。これらの量の構成は単純ですがちょっと長いので、Appendixに具体的な表式のみ掲載しておきます。

計算結果: 長さに拘束をかけない場合

まず拘束をかけないとどうなるか見ておきます。

ひもの長さに拘束をかけない場合のひもの形状のiteration依存性。空間の離散化に関し$-20\le x\le 20$を400分割している。

図3がひもの形状のiteration依存性です。一番下の青線が初期関数であり放物線$y=7/40x^2+10$に設定しています。また境界条件として$(\pm 20,80)$で$u$の値を固定しています。これを極小化のアルゴリズムであるAdamAdamを用いてフローさせています（パラメータ:$\textrm{lr}=0.005,\beta_1=0.9,\beta_2=0.999$）。iterationが進むごとに平坦になり、最終的には平らになります。下図のようにエネルギーはiterationが進むごとに小さくなります。

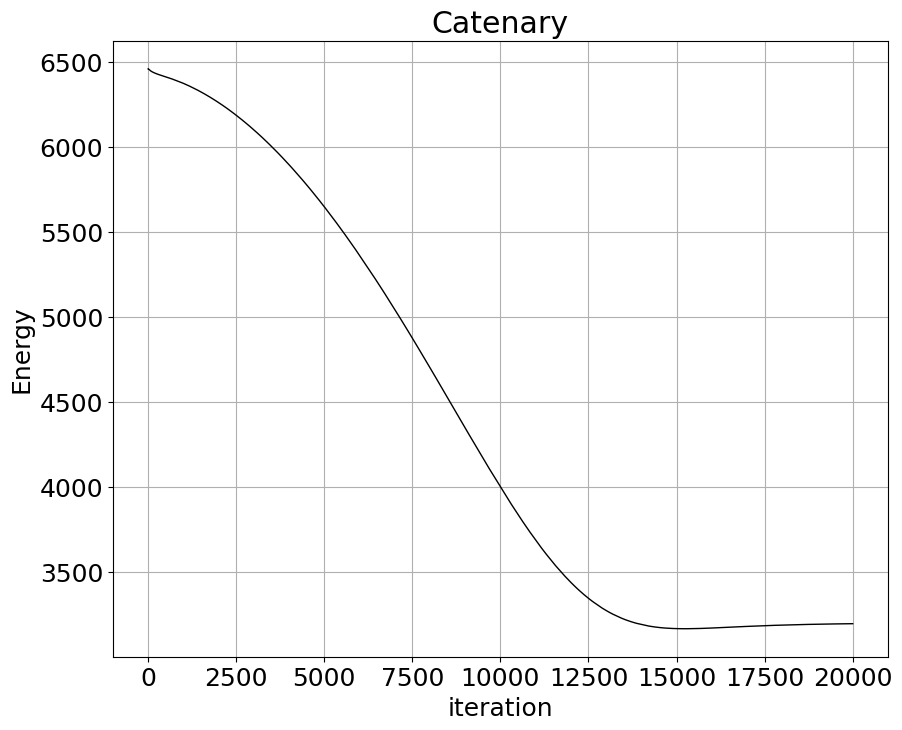図3のひものエネルギーのiteration依存性。

端を$(\pm 20,80)$に固定した場合、まっすぐにピンと張ったひものエネルギーは$80\times 40=3200 $であり、実際その辺りにエネルギーが収束しています。長さを固定しないと長さの違うひもの関数空間までサーチして極小を見つけようとするため、懸垂線には行き着かないのだと思います。

計算結果: 拘束をかけた場合

一方公式2を用いてひもの長さに拘束をかけて計算すると下図のようになります。

ひもの長さに拘束をかけた場合のひもの形状のiteration依存性。空間の離散化に関し$-20\le x\le 20$を400分割している。

紫の線が初期条件であり、図1と同じ放物線に設定しています。この放物線の長さは図のスケールで148.98です。これと同じ長さを持ち端点を$(\pm 20,80)$に固定した懸垂線が正しい解であり、灰色の太線がそれです。だいたい3回程度のiterationで概形は正しい懸垂線に到達します。またひもの長さの拘束されるべき値からの誤差はiteration16回目以降で$10^{-6}$より小さくなります。このことから拘束は正しく機能していることがわかります。

エネルギーのiteration依存性は以下のようになります：
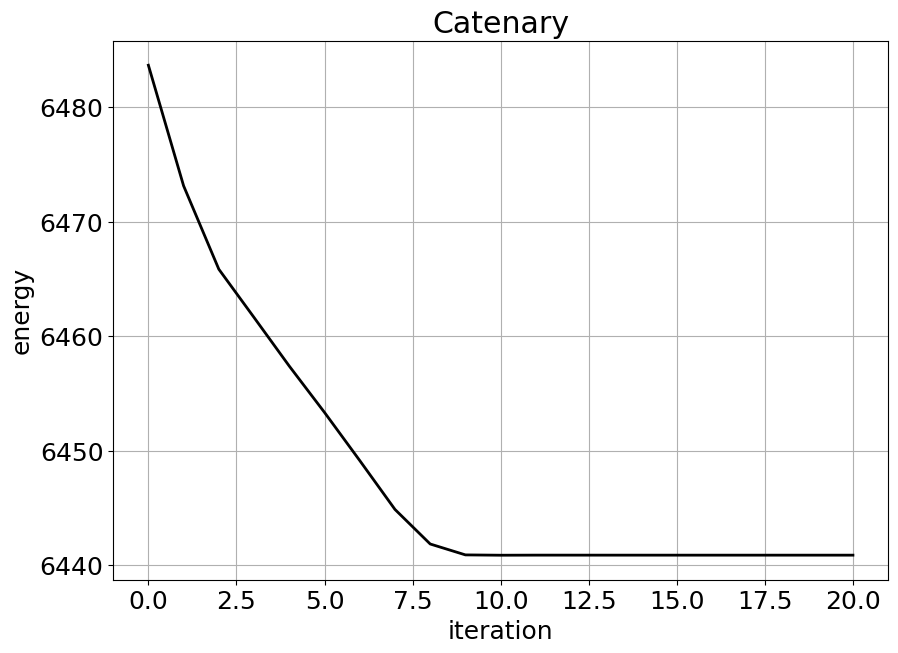図5のひものエネルギーのiteration依存性。

エネルギーは単調に減少し、だいたいiteration回数が10回で一定になります。非常に速く収束しています。

Mathematicaで計算すると、初期の放物線のエネルギーは6487、また正しい解である懸垂線のエネルギーは6476です。本計算の初期のエネルギーはだいたい良いですが、最終的に安定した後のエネルギーは6441なので、けっこう差があります。図5をよく見ると少し真の解から計算結果がずれているのが問題なのかもしれません。またはコードに問題があるかもしれません。まあでも定性的・半定量的には問題ない結果かと思います。

Newton法はiteration回数に対し非常に速く収束します。ただAdam等の陽的なminimizationと比較して、iteration毎に空間の分割数分の行と列を持つ行列の逆行列計算が必要なので、計算量は単純には比較できません。

もう少し歪な初期条件から始めても正しい形状を得ます：
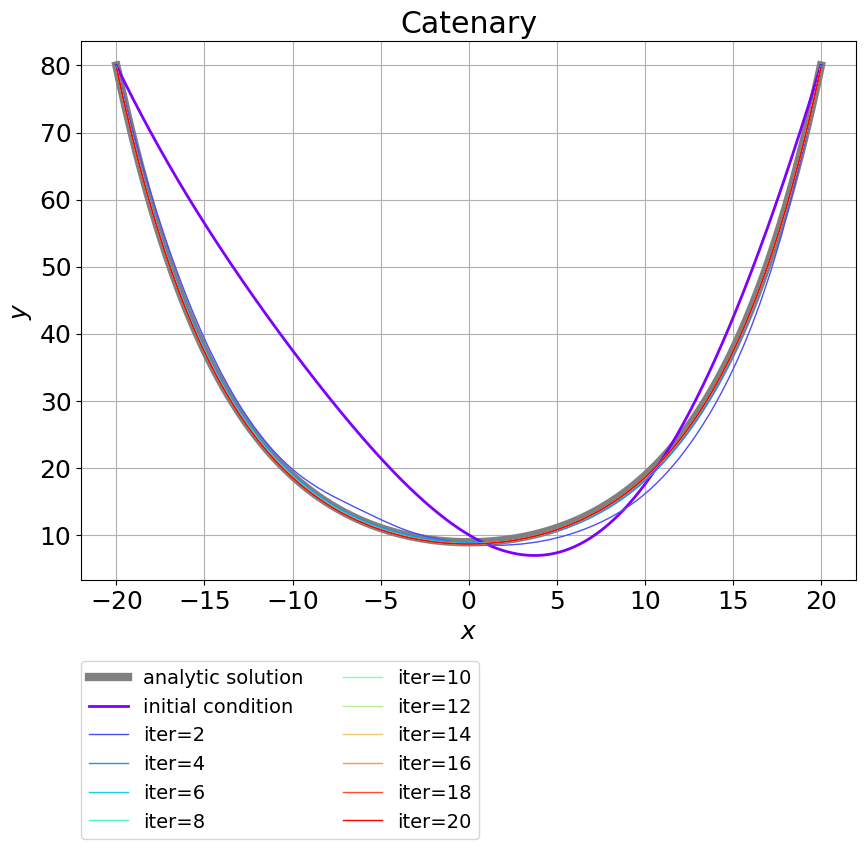図5よりも歪な初期状態からフローさせた計算。計算条件は初期条件以外図5と同じ。

計算条件は初期条件（紫の線）以外図5と同じです。この場合でもiterationが3回程度でひもの形状はほぼ正しい懸垂線に到達します。またひもの長さもiterationが13回以降では誤差が$10^{-6}$を下回り、正しく拘束がかかっています。エネルギーはiteration=0で6520、iteration10回目以降で6459で落ち着きます。一方正しい初期のエネルギーは6525、解となる懸垂線のエネルギーは6497です。やはり最終的に到達するエネルギーは正しいものより低い値になります。

図7の初期条件より更に歪んだ初期条件を与えると往々にして収束せず計算が発散して破綻します。極小化の数値計算では不安定性は頻繁に見られる現象であり気を遣う点ですWashio。またそもそもNewton法では初期条件が悪ければ収束は保証されません。ある程度良い初期条件を選ぶことは大切です。

まとめ

本記事では拘束の存在する汎関数の極小化問題を、Lagrangeの未定乗数法とNewton法により解く方法に関して述べました。多変数の場合のNewton法および未定乗数法におけるNewton法の定式化に関して記したのち、その応用として数値計算により懸垂線を求めました。この方法において、初期条件と不安定性に気を配れば、数値計算により拘束系における汎関数の極小化問題をうまく解くことができます。

Newton法+Lagrange未定乗数法で懸垂線を計算するコードをGistにアップロードしましたCode。PythonでコーディングしJupyter Notebookとして保存してあります。各セルを上から順番に実行すれば図5・6が描画されます。よろしければご参照ください。
（※本コードの正しさは保証できません。何らかの別用途に利用される場合ご自身で確認・修正されることをおすすめします）

おしまい。${}_\blacksquare$

Appendix: $\partial f/\partial \boldsymbol{u}$等の懸垂線における表式

まず$f,\varphi$を以下で定義します：
\begin{align} f&=dr\sum_i u_i\sqrt{1+((u_{i+1}-u_{i-1})/2dr)^2} \ \ \ (\text{dim.} 2),\\ \varphi&=dr\sum_i \sqrt{1+((u_{i+1}-u_{i-1})/2dr)^2} \ \ \ (\text{dim.1}) \end{align}
$dr$は本文の$\Delta x$です。$\text{dim.} n$は長さの$n$乗の次元を持つことを意味します。$dr, \ u_i$はdim. 1です。

表式の簡単化のため次の量を定義しておきます:
\begin{align} g_i:=\sqrt{1+\{(u_{i+1}-u_{i-1})/2dr\}^2} \ \ \ (\text{dim.} 0),\\ {}\\ h_i:=(u_{i+1}-u_{i-1})/2dr \ \ \ (\text{dim.} 0),\\ {}\\ \alpha:=1/(2dr) \ \ \ (\text{dim.} -1) \end{align}

以上の準備のもと、計算に必要な量は以下のようになります：

• $\partial f/\partial u_i$ (dim. 1)
  \begin{align} \frac{\partial f}{\partial u_i} =dr\left(g_i+\alpha(u_{i-1}h_{i-1}/g_{i-1} -u_{i+1}h_{i+1}/g_{i+1})\right) \end{align}

• $\partial^2 f/\partial u_i\partial u_j$ (dim. 0)
  \begin{align} \frac{\partial^2 f}{\partial u_i\partial u_j}&= \alpha dr\Bigg\{ {} \delta_{i,j+1} \frac{h_j}{g_j} {} -\delta_{i,j-1} \frac{h_j}{g_j} \\ &+\delta_{i,j-1}\frac{h_{j-1}}{g_ {j-1}} {} -u_{j-1}\delta_{i,j} \frac{h_{j-1}^2}{g_{j-1}^3}\alpha {} +u_{j-1}\delta_{i,j} \frac{\alpha}{g_{j-1}} {} +u_{j-1}\delta_{i,j-2} \frac{h_{j-1}^2}{g_{j-1}^3}\alpha {} -u_{j-1}\delta_{i,j-2}\frac{\alpha}{g_{j-1}} \\ {} &-\delta_{i,j+1}\frac{h_{j+1}}{g_{j+1}} {} +\delta_{i,j+2}u_{j+1} \frac{h_{j+1}^2}{g_{j+1}^3} \alpha {} -\delta_{i,j+2}u_{j+1} \frac{1}{g_{j+1}}\alpha {} -\delta_{i,j} u_{j+1} \frac{h_{j+1}^2}{g_{j+1}^3} \alpha {} +\delta_{i,j}u_{j+1} \frac{\alpha}{g_{j+1}} \Bigg\} \end{align}

• $\partial \varphi/\partial u_i$ (dim. 0)
  \begin{align} \frac{\partial\varphi}{\partial u_i} =\alpha dr \left\{ \frac{h_{i-1}}{g_{i-1}} -\frac{h_{i+1}}{g_{i+1}} \right\} \end{align}

• $\partial^2 \varphi/\partial u_i^2$ (dim. -1)
  \begin{align} \frac{\partial^2\varphi}{\partial u_i \partial u_j} = \alpha^2 dr \Bigg[& \delta_{i,j}\left\{ -\frac{h_{j-1}^2}{g_{j-1}^3} {} +\frac{1}{g_{j-1}} \right\} {} +\delta_{i,j-2} \left\{ \frac{h_{j-1}^2}{g_{i-1}^3} {} -\frac{1}{g_{j-1}} \right\} \\ &+\delta_{i,j+2}\left\{ \frac{h_{j+1}^2}{g_{j+1}^3} {} -\frac{1}{g_{j+1}}\right\} {} +\delta_{i,j} \left\{ -\frac{h_{j+1}^2}{g_{i+1}^3} {} +\frac{1}{g_{j+1}} \right\} \Bigg] \end{align}

以上。${}_\blacksquare$