大学数学基礎解説

反転について

反転

2609

はじめに

この記事では僕が少し授業でやった反転について書きたいと思います。
といっても僕も少しやった程度なのであまり詳しくは書けません。基礎の基礎を書きます。

ここでは、$AB$間の長さを単に$AB$と表記します。

反転とは

反転は、ある円を基準として点を別の点に移すことを言います。

定義

言葉を定義します。
・反転円：反転を行う基準となる円。
・点$K$の反転
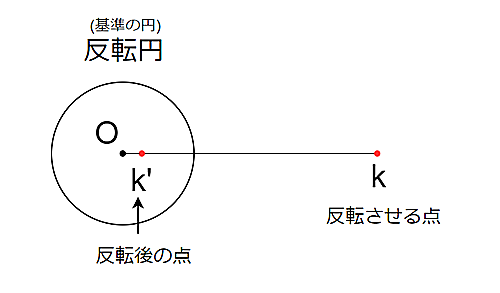反転の定義
「中心$O$で半径$r$の反転円に対して$K$を反転させる」とは
$K$に対して半直線$OK$上の$OK*OK'=r$となるような$K'$を対応させる
ということである。

この記事では簡単のため特に注意のない限り反転円の中心を$O$,半径を$1$とする。

この定義からある点を$2$回反転させると元に戻ることが分かります。

原点の反転

$O$を反転させた$O'$は$OO*OO'=0*OO'=1$を満たさなければならないが、そのような点は平面上にはないので、$O$を反転させると無限遠点になるということにする。
(無限遠点は平行な二直線の交点となるはるか遠くにある点らしいです。僕もよくわかってません…)

図形の反転

僕は直線の反転と円の反転をやったので、その二つについて書いていきます。
反転させる図形が$O$を通るかが反転をさせた後の図形にかかわってきます。

直線の反転

まずは直線を反転させるとどうなるか考えましょう！
少しイメージすれば原点を通る直線を反転させてもその直線のままだとわかります。
以下は原点を通らない直線の反転について考えます。
直線を反転させるというのは直線上のそれぞれの点を反転させるということです。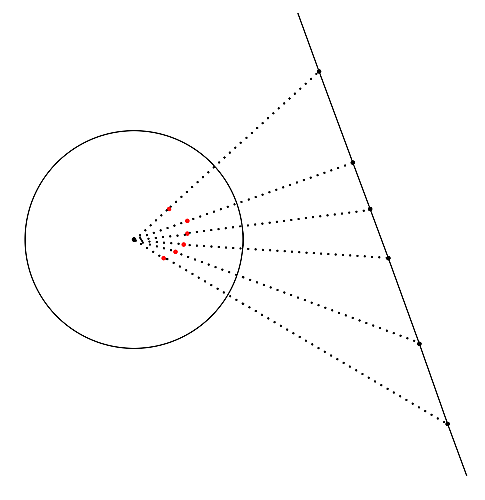直線の反転この図を見ると直線を反転させると円ができそうだと考えられますね。
そのことを証明します！

証明

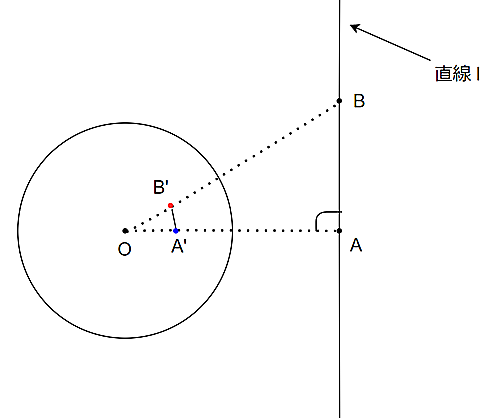直線の反転
この図で、$OA'$を直径とする円に反転されることを示す。($OA \perp l$)
また、$B$は$l$上の任意の点とする。
そして、$A$,$B$が反転して移った点を$A'$,$B'$とする。

$ \triangle OAB \backsim \triangle OB'A'$

反転の定義より、$OA'=\frac{1}{OA}$、$OB'=\frac{1}{OB}$
よって、$OA':OB'=\frac{1}{OA}:\frac{1}{OB}=OB:OA$
また、$ \triangle OAB $と$\triangle OB'A'$は$\angle BOA$を共通の角として持つので、二辺比狭角相等より相似となる。

二つの相似な三角形において対応する角は等しいので$\angle OB'A'=\angle OAB=90^{\circ}$
$\Longrightarrow$$B$は$OA$を直径とする円の円周上にある！
また、円周上の一点と$O$を結んだ直線は必ず$l$と交わるので、円が途切れるところはない。
$\Longrightarrow$$l$を反転させると$OA'$を直径とする円になる！

まとめ

・$O$を通る直線を反転させても変わらない
　・$O$を通らない直線を反転させると$O$を通る円になる。

円の反転

$O$を通る円、通らない円を反転させましょう！
下に解説が乗っていますので、少し考えてみてからスクロールしてください！
↓

$O$を通る円

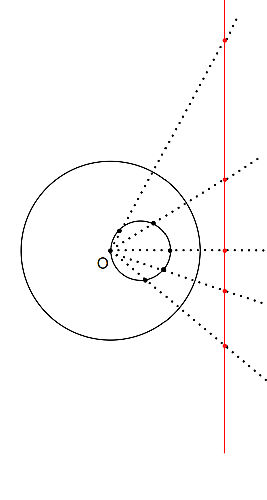円の反転
このように$O$を通らない直線になりそうですね！
証明は$O$ を通らない直線の反転の時とほとんど同じなので割愛します。ぜひ考えてみてください

$O$を通らない円

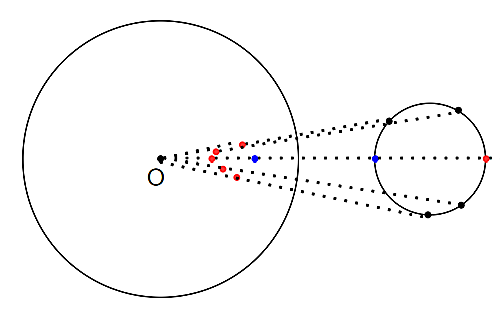円の反転
右の円を反転させると左のような点のつまりになり、これもまた円になると考えられ、それは正しいです。証明をしてみましょう。

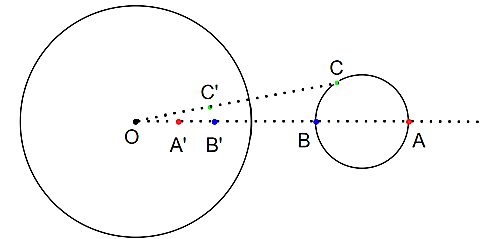証明
二点$A$,$B$は円$\Gamma$の直径で、$O$,$A$,$B$が一直線上になるようにとった点である。
また、Cは$\Gamma$上の任意の点である。
$A$,$B$,$C$が反転して移った点を$A'$,$B'$,$C'$とする。
$\angle C'A'B' =90^{\circ}$を示せばよい。
反転の定義より、$OA'=\cfrac{1}{OA}$,$OB'=\cfrac{1}{OB}$,$OC'=\cfrac{1}{OC}$
よって、二辺比狭角相等より、$\triangle OAC'\backsim \triangle OCA$,$\triangle OB'C'\backsim \triangle OCB$がわかり、
$\angle C'A'B'+\angle A'B'C'$
$=\angle A'OC'+\angle OC'A'+\angle A'B'C'$
$=\angle A'OC'+\angle CAO+\angle OCB$
$=(\angle A'OC'+\angle OCB)+\angle CAO$
$=\angle CBA+\angle CAO$
$=90^{\circ}$
なので$\angle C'A'B' =180^{\circ}-(\angle C'A'B'+\angle A'B'C')=90^{\circ}$となる。
よって、$C'$は$A'B'$を直径とする円の周上にあるので、
$O$を通らない円を反転すると$O$を通らない円になることがわかった。

ここまでのまとめ

ここまではさらっと書くつもりがまあまあ長くなってしまいました…
簡単にまとめると

\begin{eqnarray}Oを通る直線&\xrightarrow{反転}&元の直線 \\ Oを通らない直線&\xrightarrow{反転}&Oを通る円 \\ Oを通る円&\xrightarrow{反転}&Oを通らない直線\\ Oを通らない円&\xrightarrow{反転}&Oを通らない円\end{eqnarray}

僕はここまでで「だから何？」と思いました。
なのでここで一問反転の威力がわかる問題を出してこの記事は終わりにしようと思います！！
としたかったのですが記事が長くなってしまったので二つに分けることにして今回はここで終わります。