図形の問題

まえがき

ここの問題は 前回の記事 で説明した手法を使う図形問題を出します。復習問題のようなものですが、前回説明した方法を知らないと難しいかもしれません。
本当は上の記事で出したかったのですが、結果が面白くなったのとその記事が長くなったのとでここで問題を出すことにします。

問題

問$1$ 問題
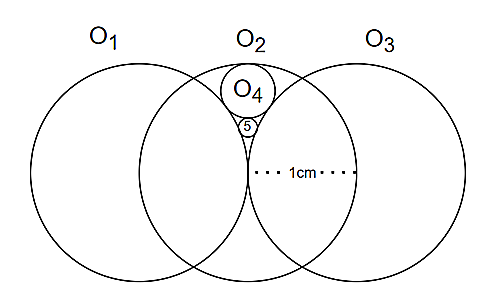
注意：$O_5$とは、円の中に$5$と書かれているものとする。($O_5$と書こうとすると字が入りませんでした)
右の図で、$O_1$,$O_2$,$O_3$の半径は等しく、$O_1$と$O_3$は$O_2$の中心で交わっている。
$O_4$は$O_1$,$O_2$,$O_3$に接していて、$O_5$は$O_1$,$O_3$,$O_4$に接している。
このとき、$O_5$の直径を求めなさい。

問$2$
問題2
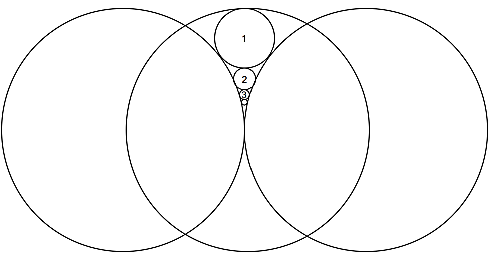
問一のような構成を繰り返してできる円を$n$個作り、順に$1,2,3\dots n$とした。
$n$の直径を求めよ。

解説

まず、この問題を解く際に僕が前回説明を載せた反転を使います。反転についてよく知らない方はまず こちら から見てみてください！(この記事を見たらこの問題はすぐ解けるかもしれません。)

そう、反転を使うとこれが一瞬で解けます！！！(たぶん計算しても解けますがとても複雑になると思います。)
まず少しおさらいです。反転したときの関係はこのようになります。

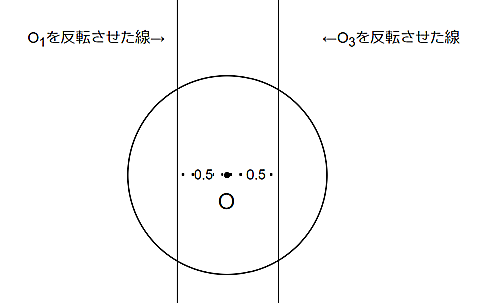
解説1

まず、$O_1$と$O_3$は$O$を通る円なので反転すると$O$を通らない直線となり、また$O$からの距離は$0.5$だということが簡単にわかる。

これを使って考えてみましょう！

$O_4$の反転先はどこかを考えます。
まず、$O_4$は$O$を通らない円なので$O$にを通らない円に移ります。
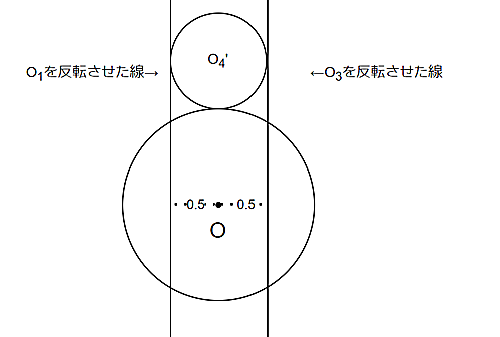
そして、$O_4$は$O_1$,$O_2$,$O_3$に接していて、反転前に$O_4$と$O_1$が接していた点は反転後も同じ位置にあるので$O_4$を反転させた$O_4'$は下の図のようになります！ 解説2

また、$O_5$の反転先も同じように考えます。
$O_5$は$O$を通らない円なので$O$にを通らない円に移ります。
そして、$O_5$は$O_1$,$O_3$,$O_4$に接していて、反転前に$O_5$と$O_4$が接していた点は$O$から縦に引いた直線上(厳密にいうと、$O$から$O_1$を反転させた線に平行に引いた直線上)にある$O$に近い側の点なので、反転後は$O$から遠いほうの点に移る。よって、 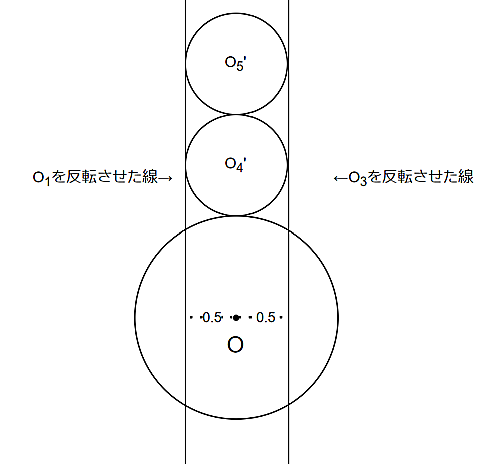解説3 $O_5$を反転させた$O_5'$は図のようになります！！

$O_4'$,$O_5'$は半径$1$の円とわかるので、それを反転前に戻すと 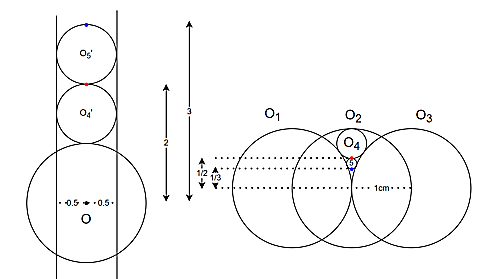解説4
よって、$O_5$の直径は$\d \frac{1}{2}-\frac{1}{3}=\frac{1}{6}$となります。

$2$番も同じです。
真ん中の円を円$\Gamma$としてそれを基準に反転すると 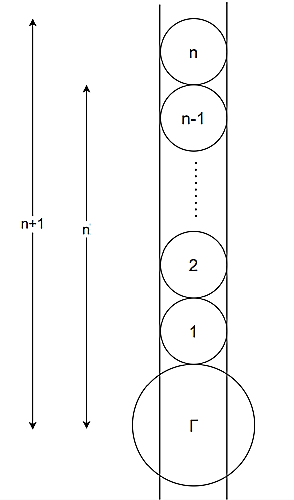解説
このようになる。よって$n$の直径は$\d \frac{1}{n}-\frac{1}{n+1}=\frac{1}{n(n+1)}$となります。

最後に

いかがでしたでしょうか。円が組み合わさってきれいな図形でしたが、直径もまたきれいな値になりました！すごいですね！
　最後まで読んでいただきありがとうございました！