カタラン数とその拡張 その4 〜ロビンソン対応と321-avoiding permutation〜
「カタラン数とその拡張」シリーズ2年ぶりの投稿になります。
前回(その3)
は、ヤング図形・標準盤といった用語を定義し、次の命題から出発してカタラン数の拡張を行いました。
$2\times n$の長方形の形をした標準盤($2\times n$のマス目に$1$から$2n$までの数字を入れたもので、各行、各列が単調増加なもの)の個数は、カタラン数$c_n$に等しい。
今回は、321-avoiding permutationというものについて話していこうと思います。ヤング図形を使いますが、前回の記事を読んでいなくても読めると思います。ただし命題1は使うので、分からなければ その1 を参照してください。
321-avoiding permutation
$1,2,3,\cdots,n$の並び替えのうち、長さ3の減少部分列を持たないものの個数を321-avoiding permutationという
たとえば、$21354$はどの3数を選んでも降順になっていないため321-avoiding permutationです。$34251$は$3,2,1$や$4,2,1$という減少部分列をもつため321-avoiding permutationではありません。
この記事の目標は、次の定理です。
長さ$n$の321-avoiding permutationの個数は$n$番目のカタラン数$c_n$に等しい
証明の準備
クヌース変換
以下、相異なる自然数からなる有限数列を数字列と呼ぶことにします。
数字列$w = x_1 x_2 \cdots x_n$の減少部分列であって、その長さが最も大きいものを最長減少部分列(LDS)といい、その長さを$L(w)$で表す。
$L(25431)=4,\quad L(12345)=1$
$1,2,3,\cdots,n$の並び替え$w$のうち、$L(w) \leq 2$となるものの個数を求めるのが今回の目標です。
突然ですが、次のような数字列の同値関係を定義します。
数字列$w$を考える。次の操作をクヌース変換という。
数字列$w$と$w'$がクヌース変換の繰り返しで移り合うとき、$w$と$w'$はクヌース同値であるという。
クヌース変換は、最長減少部分列の長さ$L(w)$を保つという著しい性質があります。
$w$と$w'$がクヌース同値なとき、
$w'$が$w$に一回のクヌース変換を行ったものとして一般性を失わない。$u=u_1 u_2\cdots u_p,v=v_1 v_2 \cdots v_q$を適当な数字列として、対称性から2通りの場合に帰着できる。
(i)
と書ける場合。まず、$w'$の減少部分列はそのまま$w$の減少部分列になるから、
(ii)
と書ける場合。まず、$w'$の減少部分列はそのまま$w$の減少部分列になるから、
バンプアルゴリズム
ここからはヤング図形の話です。 前回 導入した、ヤング図形・標準盤の定義を再掲しておきます。
広義単調減少する自然数の組$(k_1,k_2,k_3,\cdots,k_n)$に対し、下図のように$i$行目に$k_i$個の単位正方形(箱)を並べた図形をヤング図形という。
![!FORMULA[67][1451206170][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220330235618.png?alt=media) $(5,4,2)$
$(5,4,2)$
$n$個の箱からなるヤング図形に、各行、各列が左から右、上から下に単調増加となるように、$1,2,3,\cdots,n$を1つずつ書き込んだものを標準盤という。
標準盤の条件を緩めて、書き込まれる数字を自由にした「盤」を定義します。
ヤング図形に相異なる数字を書きこんだもので、標準盤と同様に各行、各列が単調増加であるものを盤と呼ぶことにする
注:「盤」という用語はこの記事独自のものです。「半標準盤」という似た概念がありますが、これは同じ数字が複数入るのを許します。
盤$T$に対し、数字を下から上に、左から右に読んでいってできる数字列を$T$のワードといい、$w(T)$で表す。
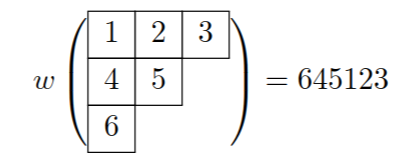
$T$を盤、$x$を$T$にない数字とします。バンプは$T$と$x$から新しい盤$T \leftarrow x$を作る操作で、つぎのように定義します。
- $a_1 = x$とする。
- $i=1,2,3,\cdots$に対して、次の操作を繰り返す。
- $T$の$i$行目に箱がないか、$i$行目の右端の数字が$a_i$より小さい場合は、$a_i$を$i$行目の右端に置いて繰り返しを終了する。
- そうでない場合、$i$行目のうち$a_i$より大きい最小の整数を$a_{i+1}$とし、$a_{i+1}$の入った箱を$a_i$で置き換える。
- 最終的に得られた新しい盤を$T \leftarrow x$と定義する。
$T \leftarrow x$が盤の条件を満たすことを確認する必要がありますが、ここでは省略します。
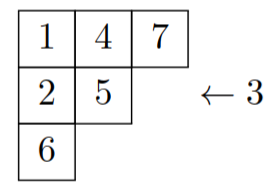
を計算したいとします。上記のアルゴリズムにより、
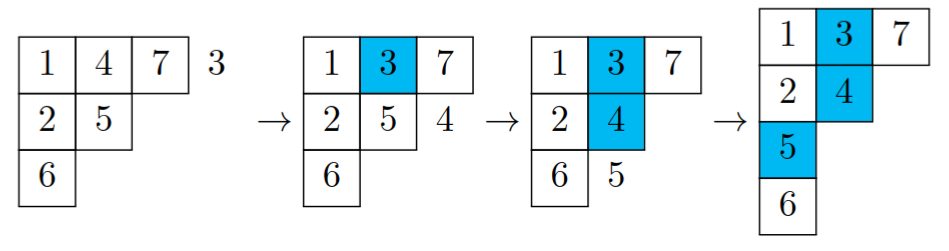
となります。ヤング図形の外に書かれた数字が$a_i$で、$a_1=3, a_2=4, a_3=5, a_4=6$です。置き換えられた数字を青色で示しています。これより、

であることがわかります。
次に、数字列$w$から$P(w)$と書かれる盤を作る手順を紹介します。
数字列$w = x_1 x_2 \cdots x_n$に対し、$x_1$の入った箱に$x_2, x_3, \cdots, x_n$を順番にバンプして得られる盤を$P(w)$と定義する。すなわち、
$$
P(w) := (\cdots ((\fbox{$x_1$} \leftarrow x_2) \leftarrow x_3) \leftarrow \cdots) \leftarrow x_n
$$
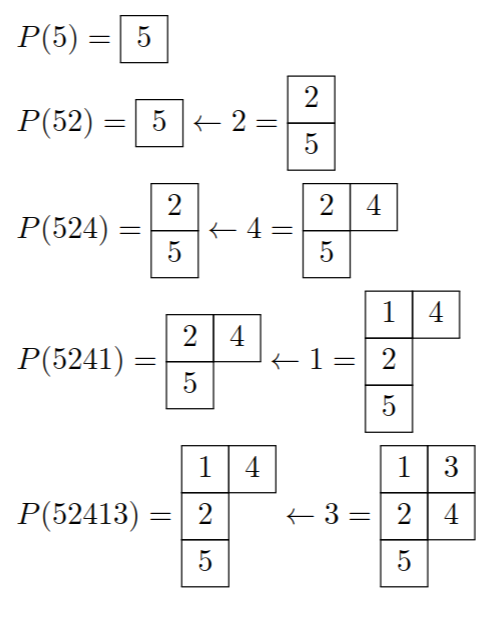
実は、$P(w)$はクヌース同値類を考える際に重要な役割を果たします。
任意の数字列$w$に対し、$w$と$w(P(w))$はクヌース同値である。
一般的に述べるのは面倒なので、具体例での説明に留めます。
$P(w) \leftarrow x$のワードと$wx$がクヌース同値であることを示せば帰納法により十分である。そのために、バンプアルゴリズムの過程をクヌース変換のみで記述できることを示せば良い。バンプアルゴリズムの1ステップにあたる

が、対応する数字列のクヌース変換だけで実現できる様子を示す。それぞれに対応する数字列は、
$$
(89|123567\ 4),\quad (89\ 5|123467)
$$
である。(行の区切りを$|$で示している。)まず、
$$
(89|123\textcolor{red}{5}\underline{67\ \textcolor{blue}{4}}) \to (89|123\underline{\textcolor{red}{5}6\textcolor{blue}{4}}7) \to (89|123\textcolor{red}{5}\textcolor{blue}{4}67)
$$
のように、バンプする数字$a_1=4$を$a_{2}=5$のすぐ後ろまで移動させることができる。これらの変換はすべて、
$$
xyz \to xzy\quad (y>x>z)
$$
の形をしたクヌース変換である。次に、
$$
(89|12\underline{3\textcolor{red}{5}\textcolor{blue}{4}}67) \to (89|1\underline{2\textcolor{red}{5}3}\textcolor{blue}{4}67) \to (89|\underline{1\textcolor{red}{5}2}3\textcolor{blue}{4}67) \to (89|\textcolor{red}{5}123\textcolor{blue}{4}67) = (89\ \textcolor{red}{5}|123\textcolor{blue}{4}67)
$$
のように、$a_{2} = 5$を$2$行目の右端まで移動させることができる。これらの変換はすべて、
$$
xyz \to yxz\quad (y>z>x)
$$
の形をしたクヌース変換である。このように、バンプアルゴリズムは、対応する数字列のクヌース変換だけで実現できることがわかった。
実は、任意の数字列$u,v$に対し、$P(u)=P(v)$であることと$u,v$がクヌース同値であることが同値になります。これより、盤と数字列の同値類が自然に一対一対応することが分かります。これの証明はしません。詳細はWilliam FultonのYoung Tableauxを参照してください。
$L(w)$は、$P(w)$の行数に等しい。
$L(w)$は$w' := w(P(w))$とクヌース同値なので、$L(w')$を求めればよい。$P(w)$の行数を$l$とする。
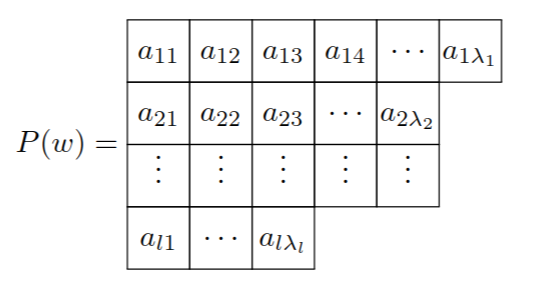
としよう。$w'$は
$$
w' = (a_{l1} a_{l2} \cdots a_{l \lambda_{l}}| \cdots | a_{21} a_{22} \cdots a_{2 \lambda_2} | a_{11} a_{12} \cdots a_{1 \lambda_2})
$$
と書ける。まず、$P(w)$の各行の左側の数字を並べた$
a_{l1}\cdots a_{31}a_{21}a_{11}
$は、$P(w)$の減少部分列を与えるので、$L(w') \geq l$である。また、$w'$の部分列を作る際、$P(w)$の同じ行から$2$つ以上の数字を選ぶと減少部分列とならないので、$L(w') \leq l$である。以上より、$L(w) = L(w') = l$である。
これより、次の系を得ることができます。
$1,2,\cdots,n$の並び替え$w = x_1x_2 \cdots x_n$が321-avoiding permutationであるための必要十分条件は、$P(w)$の行数が$2$以下であることである。
ロビンソン対応
バンプの重要な性質は、それが可逆であるということです。
バンプによって生じた盤$T \leftarrow x$と新しく追加された箱の位置$B$が与えられたとき、$T,x$を復元することができる。
証明は単にバンプアルゴリズムを逆向きに走らせるだけです。
- $T'$において$B$のある位置を$l$行目とし、$B$に入った数字を$a_{l}$とおく。箱$B$を取り除く。
- $i=l-1,\cdots,3,2,1$に対して、次の操作を繰り返す。
- $i$行目のうち$a_{i+1}$より小さい最大の整数を$a_i$とし、$a_i$の入った箱を$a_{i+1}$で置き換える。
- 最終的に得られた盤を$T$とし、$x = a_1$とする。

また、この逆バンプアルゴリズムは常に行うことができます。すなわち、任意の盤$T'$と$T'$の角$B$が与えられたとき、$T' = T \leftarrow x$で、$T'$にあって$T$にない箱が$B$であるような$T,x$がただ一つ存在します。また、数字列$w$から$P(w)$を作る際、$P(w)$と箱が追加された順番が分かれば、そこから数字列$w$を復元できます。これにより次の重要な定理が導かれます。
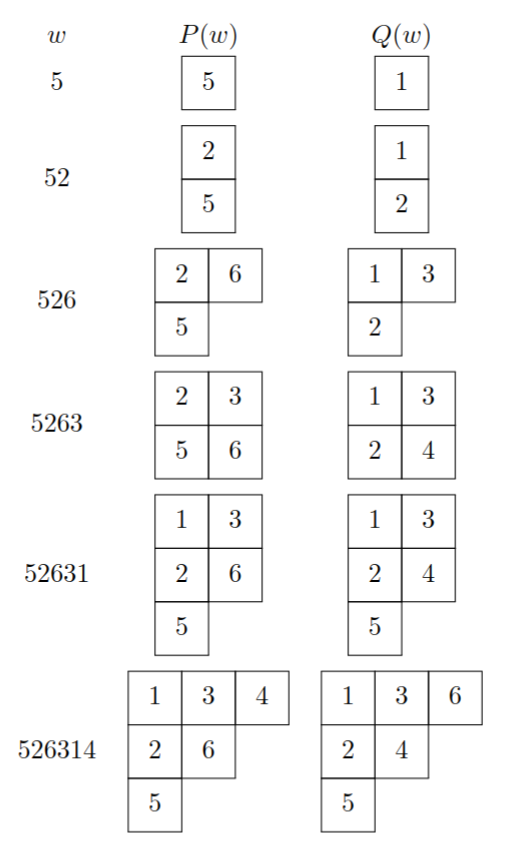
$n$個の箱からなる同じ形の標準盤の組$(P,Q)$と、$1,2,\cdots,n$の並び替えの間に自然な一対一対応がある。これをロビンソン対応という。
$1,2,\cdots,n$の並び替え$w$に対して、バンプアルゴリズムによって得られる標準盤を$P=P(w)$とする。$Q=Q(w)$は$P$と同じ形をした標準盤で、$P$を作る際のバンプアルゴリズムで$k$番目に追加した箱に数字$k$を書き込んだものとする。これにより$w$から標準盤の組$(P,Q)$を得ることができる。$(P,Q)$から$w$を復元するには、単に$Q$から最大の数字の入った箱を取り除き、$P$で対応する箱に対して逆バンプを行うことを繰り返せば良い。
ここから、次の系が得られます
長さ$n$の321-avoiding permutationの個数は、行数が$2$以下の、同じ形をした標準盤の組$(P,Q)$の個数に等しい
$w=526314$で$P(w),Q(w)$をもとめると、次のようになる。
定理の証明
長さ$n$の321-avoiding permutationの個数は$n$番目のカタラン数$c_n$に等しい
$2\times n$の長方形の形をした標準盤の個数は、カタラン数$c_n$に等しいので、これと行数が$2$以下の、同じ形をした標準盤の組$(P,Q)$が一対一に対応することを示せば十分である。この対応は簡単に作ることができる。
標準盤の組$(P,Q)$に対し、$Q$の各数字$k$を$k^* :=n+1-k$に置き換え、それを$180$度回転させた図形を$Q^*$とする。$P$の右に$Q^*$をはめ込むと、$2\times n$の長方形の形をした標準盤$T$を得ることができる。

逆に$2\times n$の長方形の形をした標準盤$T$が与えられた時、$T$のうち$n$以下の数字からなる部分$P$とそれ以外の部分$Q^*$とに分ける。$Q^*$の各数字$k$を$k^*$に置き換え、それを$180$度回転させた図形を$Q$とすれば、標準盤の組$(P,Q)$を得ることができる。これらが互いに逆写像を与える。
ここからおまけ
カタラン数の拡張
今回の話を踏まえて、次のようなカタラン数の拡張を考えることができます。
$1,2,3,\cdots,n$の並び替えのうち、長さ$k+1$の減少部分列を持たないものの個数を$D(n,k)$とする
$D(n,1)=1, D(n,k)=c_n$です。一般の$D(n,k)$については、次のような表式が存在します。
$$
D(n,k) = \frac{1}{k!}\sum_{l_1+l_2+\cdots+l_k=n+\frac{k(k-1)}{2}} \left(\frac{n! \prod_{i< j}(l_i-l_j)}{l_1! l_2! \cdots l_k!}\right)^2
$$
ここで$l_1,l_2,\cdots,l_k$は$l_1+l_2+\cdots+l_k=n+\frac{k(k-1)}{2}$なる非負整数全体を動くとする。
これ以上簡単にできるかは不明です。
証明
$k=2$の場合と同じ理由で、$1,2,3,\cdots,n$の並び替えのうち、長さ$k+1$の減少部分列を持たないものは、高々$k$行からなる同じ形の標準盤の組と対応します。したがって、形がヤング図形$\lambda$である標準盤の個数を$\mathrm{SYT}_{\lambda}$とすれば、
次のように書くことができます。
$$ D(n,k) = \sum_{\lambda} (\mathrm{SYT}_{\lambda})^2 $$
ここで$\lambda$は、箱の個数が$n$で高々$k$行からなるヤング図形全体を動きます。
ここで使えるのが、 前回 証明したフック長公式です。
$n$個の箱からなるヤング図形$\lambda$とその箱$c \in \lambda$について、
- $c$
- $c$と同じ行で$c$より右にある箱
- $c$と同じ列で$c$より下にある箱
を合わせた集合を$c$のフックと言う。フックに含まれる箱の個数を$h_{\lambda}(c)$で表すことにすれば、
$$
\mathrm{SYT}_{\lambda} = \frac{n! }{\prod_{c \in \lambda}h_{\lambda}(c)}
$$
である。
この定理の証明は前回の記事を参照してください。このままでは使いにくいので、次のような別の表示を与えましょう。
$n$個の箱からなり$k$行以下のヤング図形$\lambda$について、$i$行目の箱の個数を$\lambda_i, \quad a_i:=\lambda_i+k-i \quad (i=1,2,\cdots,k)$とするとき、
$$
\mathrm{SYT}_{\lambda} = \frac{n! \prod_{i< j}(a_i-a_j)}{a_1! a_2! \cdots a_k!}
$$
まずはこの定理を証明するための補題を示します。
$\lambda$を$k$行$l$列のヤング図形とする。$\lambda$の$i$行目の箱の個数を$\lambda_i$、$j$列目の箱の個数を$\mu_j$と書くとき、$k+l-1$個の整数
には$1,2,\cdots,k+l-1$が一つずつ現れる。
注:$i=1$も動かしたほうが美しいですが、証明の都合上$i \geq 2$としました。
これらが$1$以上$k+l-1$以下の整数であることは簡単に分かる。$l-\lambda_i+i-1$は$i$について狭義単調増加で、$l-j+\mu_j$は$j$について狭義単調減少なので、
$$
l-\lambda_i+i-1 = l-j+\mu_j
$$
なる$i,j$が存在しないことを示せばよい。このような$i,j$が存在したとする。この式を変形すれば、
$$i+j-1 = \lambda_i + \mu_j$$
である。ここで、もし$(i,j)$ ($i$行$j$列)が$\lambda$の箱であれば、$i \leq \mu_j, j \leq \lambda_i$であり、
$$
i+j -1 < i+j \leq \lambda_i + \mu_j
$$
となる。また、もし$(i,j)$が$\lambda$の箱でなければ、$i > \mu_j, j > \lambda_i$であり、
$$
i+j -1 > (i - 1) + (j - 1) \geq \lambda_i + \mu_j
$$
となる。これは矛盾である。したがって、題意は示された。
フック長公式より、
$$
\prod_{\lambda \in c} h_{\lambda}(c) = \frac{a_1!a_2!a_3!\cdots a_k!}{\prod_{i< j}(a_i-a_j)}
$$
を示せば良い。$k$についての帰納法で示す。そのためには、$a_1$に関わる因子の積が第一行のフック長の積であること:
$$
\prod_{j=1}^{k} h_{\lambda}(1,j) = \frac{a_1!}{\prod_{j=2}^{k}(a_1-a_j)}
$$
を示せば十分である。$h_{\lambda}(1,j) = l - j + \mu_j$であるから、補題より、
$$
\prod_{j=1}^{k} h_{\lambda}(1,j) = \prod_{j=1}^{k} (l - j + \mu_j) = \frac{(k+l-1)!}{\prod_{i=2}^{k} (l-\lambda_i+i-1)} = \frac{a_1!}{\prod_{i=2}^{k} (a_1 - a_i)}
$$
$$ D(n,k) = \frac{1}{k!}\sum_{l_1+l_2+\cdots+l_k=n+\frac{k(k-1)}{2}} \left(\frac{n! \prod_{i< j}(l_i-l_j)}{l_1! l_2! \cdots l_k!}\right)^2 $$
定理11より、
$$
D(n,k) = \sum_{\lambda} (\mathrm{SYT}_{\lambda})^2 = \sum_{\substack{l_1+l_2+\cdots+l_k=n+\frac{k(k-1)}{2} \\ l_1 >l_2>\cdots > l_k}} \left(\frac{n! \prod_{i< j}(l_i-l_j)}{l_1! l_2! \cdots l_k!}\right)^2
$$
ここでシグマの中身の$\left(\frac{n! \prod_{i< j}(l_i-l_j)}{l_1! l_2! \cdots l_k!}\right)^2$は、$l_1,l_2,\cdots,l_k$の対称式で、$l_i = l_j, i \neq j$なる$i,j$があるとき$0$なので、
$$ D(n,k) = \frac{1}{k!}\sum_{l_1+l_2+\cdots+l_k=n+\frac{k(k-1)}{2}} \left(\frac{n! \prod_{i< j}(l_i-l_j)}{l_1! l_2! \cdots l_k!}\right)^2 $$
Dyckパスとの対応
長々証明してきましたが、実はもっと簡単に321-avoiding permutationとDyckパスの対応をつくることもできます。ヒントとなる図を載せておきます。
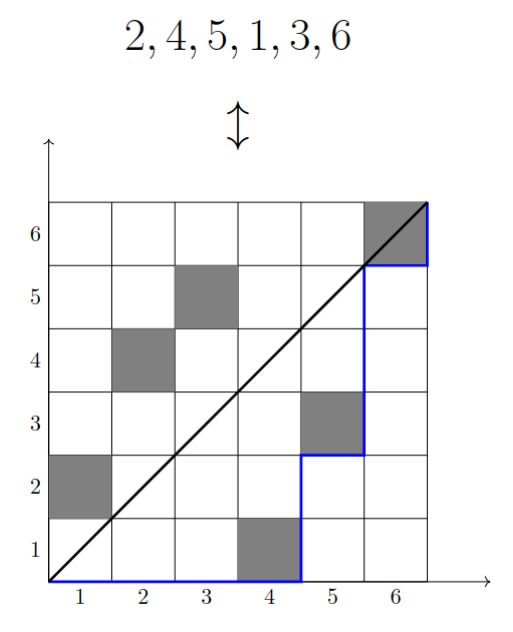
この方法は直感的ですが、証明は意外と手順が多く大変です。詳しくはRichard P. StanleyのEnumerative Combinatoricsなどを参照してください。
まとめ
カタラン数たのしい!