テンソルネットワークで紡ぐ宇宙~2.くりこみの数理~
みなさんこんにちは。Hiroです。前回の記事は こちら
量子古典対応を経て
前回の量子古典対応の章では、テンソルネットワークの描像が時空の変換と古典・量子間の変換とを結びつける働きを持っていることを見てきました。最初は単なる計算手法のように思えたテンソルネットワークの記法が、理論的バックグランドを理解するための道具にもなり得ることを端的に表す例だと思います。
テンソルネットワークは「優れた数値解析手法」と「本質的な物理描像の抽出」という二つの側面を持った理論になっています。今回もその二面性を意識しながら記事を見てもらえると嬉しいです。
くりこみ
テンソルネットワークはできた、それで?
前回の記事
の2次元イジング模型の図を思い出してみましょう。
 2次元イジング模型の分配関数
2次元イジング模型の分配関数
この図にはざっくり$5\times 5 \times 2=50$本くらいの線(ボンド)が含まれています。一つ一つはアップダウンの2通りとはいえ、愚直に$2^{50}$通り計算するのは不可能に近いです。もちろん最初の例のように転送行列などを使って簡単に計算できる場合もありますが、一般の場合にはどうすれば良いでしょうか?
ここで重要になるのがくりこみの考え方です。一般に物理学において「くりこみ」という言葉を使った時の意味合いは、物理量を再定義することによって適当な有効理論を得ることを指しますが、その際に多くの場合で適切な自由度の削減を行います。
カシミール効果とかのくりこみは自由度の削減とはまた違うような気がしています。
テンソルネットワークにおけるくりこみは、この適切な自由度の削減に根差した概念です。再帰的に計算を行なっていく中で、逐次的に自由度を削減していき、毎回の計算のオーダーをうまく抑えることによって、良い近似精度で値を求めることができます。
今回の記事では、このようなくりこみの手法として、2次元系の空間くりこみとしてCTMRGを、1次元系の時間発展に対するくりこみとしてDMRGについて取り扱い、その計算精度と対応関係について見ていこうと思います。
特異値分解
本題に入る前に、今回の主役である特異値分解という概念について紹介しておきましょう。
任意の行列 $A$ に対して、あるアイソメトリ $U, V$ と対角行列 $\Sigma$ が存在して、
$A = U \Sigma V^\dagger$
と分解することを特異値分解と呼び、$\Sigma$ の対角成分を特異値と呼ぶ。
ここでアイソメトリとは以下の式を満たす正方行列とは限らない行列のことを指す。
$U^\dagger U = I$
特異値は非負の実数であり、大きい順に $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_k \ge 0$ としておくことにします。固有値分解は、正方行列に対してのみ定義されるのに対し、特異値分解は任意の行列に対して定義することができます。
これからの計算では、テンソルの足を適当に2つのグループに分けることで、あたかもそれが行列であるかのようにみなし、そこに特異値分解を行うということをたくさん行なっていきます。特異値は固有値分解での固有値と同じように、どの要素がどれくらいの重みを持っているかということを表すので、特異値の上から適当な数までの成分だけを採用して残りを無視することによって、物理系にとって重要な部分だけを残して次元を落とすことができるのです。この「任意の行列に対して適用できて、重要な要素がどれかわかるようにしてくれる」という性質が、複雑な形のテンソルを取り扱うのに優れているのです。
以下では特異値分解とアイソメトリーに対して以下のような描像を用いていきます。
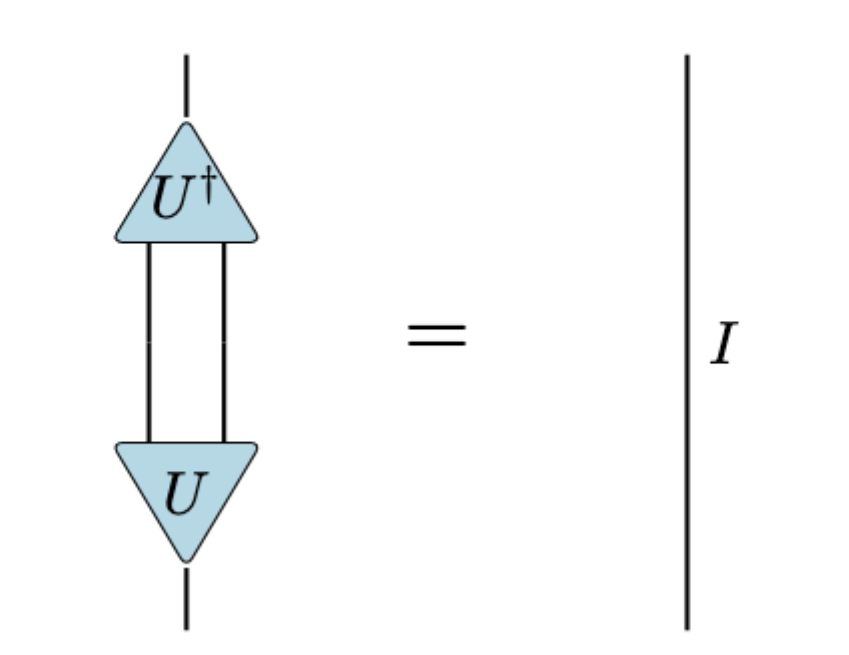 アイソメトリーの定義、三角形のやつがアイソメトリーです。中央では線が2本出ているのはランク落ちが発生していることを表しています。
アイソメトリーの定義、三角形のやつがアイソメトリーです。中央では線が2本出ているのはランク落ちが発生していることを表しています。
 特異値分解のダイアグラム
特異値分解のダイアグラム
ここより後に関しては僕のTikz力不足により、手書きの図が多くなってきます。ご了承ください。
CTMRG
CTMRGの基本概念
CTMRG(角転送行列くりこみ群)はその名の通り、転送行列を全体の角の方から順に丸め込んでいく手法になっています。その計算手順を順番に見ていきましょう。
まずは先ほどの2次元のテンソルネットワークを持ってきて、その左下の付近に注目してみましょう。境界条件に関しては先に縮約をとってしまって、足の数を減らしておくことにします。
この時に、試しに各辺の外側から2層分のテンソルと、角の4つのテンソルをひとまとめにしてしまいましょう。
 最初のステップ。点線に従って縮約をとる
最初のステップ。点線に従って縮約をとる
![取った後。赤い部分は2本分の足の自由度がまとまっているので、!FORMULA[9][1125850968][0]次元になっている](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fwg5zhlv0yqPaqnLzIZr7.png?alt=media) 取った後。赤い部分は2本分の足の自由度がまとまっているので、$d^2 $次元になっている
取った後。赤い部分は2本分の足の自由度がまとまっているので、$d^2 $次元になっている
こうすると、角から1層分少なくなった形式が得られます。これを繰り返していけば最終的には$3\times 3$程度の小さなテンソルネットワークの計算に落とし込めそうですよね。
 最終的な形
最終的な形
しかしこれにも問題があります。上の図で元の黒い線と赤い線では引数の数が違うことに気が付いたでしょうか。普通に計算をしていくと、この部分は内部のテンソルを取り込むごとにボンド次元を増やしていってしまい、計算回数は指数的に膨らんでいってしまいます。
それを対策するために必要なのが適切な自由度の削減です。最初にある適当な数$\chi$を最大のボンド次元として持っておきます。そして、マイステップごとに角を対角化し、上から$\chi$個の成分だけを残してあげるような処方箋をすることにしましょう。こうすることで、次元の爆発を抑えながら、良い精度で近似ができると考えられるわけです。
具体的な計算とダイアグラムのフロー
以下のダイアグラムでは、黒い線であればそこの次元は$d$か$\chi$、赤い線であればそれらの掛け算以上の次元を持っています。
先ほどの図を使いながら計算ステップを見ていきましょう。
- まずは角の4つのテンソルについて和をとる。
$\tilde{C}=\sum_{1,7,3,9} C_{1,7}T_{1,9,2}T_{7,3,8}A_{3,9,4,10}$
その後、もともと$T,A$から出ていた2つ分の足の自由度をまとめてしまい、$d^2$(もしくは$\chi\times d$)次元の足にする。
端っこ以外の$T$についても同様に内側のAと和を取る。
$\tilde{T}=\sum_{11} T_{2,11,13}A_{4,11,14,12}$など
 足の数字は式中と対応しています
足の数字は式中と対応しています
2. 空間の等方性を仮定すると角の行列について対角化を行うことができる。この時、大きい方から$\chi$個のみを採択するようにし、固有ベクトルの集合である$U$については、採択された固有値に対応する固有ベクトルのみを残すようにする。すると、この行列は自然にアイソメトリーになる。(下図の三角形)
$U\tilde{C}U^\dagger$で対角化されるとした時、$U$のうち大きい固有値に対応する固有ベクトルだけ残した行列$\tilde{U}$を考えれば、$\tilde{U}\tilde{C}\tilde{U}^\dagger$は削減された固有値行列になる。
 アイソメトリーによる自由度の制限
アイソメトリーによる自由度の制限
3. このアイソメトリーUを使って$\tilde{T}$も更新を行う。これによって、角以外でも$\tilde{T}$から出ていた足が同じボンド次元$\chi$まで落ちる。
$T'=\sum_{10,5}U_{9,10}\tilde{T}_{10,7,5}U^\dagger_{5,13} $など
 次元を落とした後
次元を落とした後
以上の3ステップによってボンド次元を増やさない($\chi\times d$とかが出てこない)ままで外側の一段分減らすことができました。これを4つの角で再帰的に続けていけば、最後には以下の図のようになるはずです。
 さっきのテンソル
さっきのテンソル
これはただの$3\times 3$のテンソルなので、愚直に計算してあげることができます。以上の過程で近似を入れているのは$\chi$をどれくらい大きく取るかという点だけなので、近似精度は$\chi$に依存します。
計算量と近似精度
計算量を考えるにあたっては一番重い計算はどこなのかということを考えてあげる必要があります。今回の場合は対角化です。
対角化する前の、一つ内側の層を取り込んだ行列は$(\chi d)\times(\chi d)$の次元を持っています。これを対角化の時間オーダー$\mathcal{O}(N^3)$に代入してあげると$ \mathcal{O}(\chi^3d^3)$が得られます。
あとはこれを大体系の一辺の長さ$L$回くらい繰り返すので、最終的な計算量は$ \mathcal{O}(L\chi^3d^3)$程度になります。
また空間計算量、つまりメモリの使用量に関しては、一時的に発生する$(\chi d)\times(\chi d)$の角転送行列が最大の次元数を持つので、$ \mathcal{O}(\chi^2 d^2)$になります。一方で近似精度に関しては、固有値分解における固有値スペクトル(エンタングルメントスペクトル)の分布が極めて重要になります。なぜなら、固有値の減衰の速さは、対象とする系の物理的性質(特にエネルギーギャップの有無)と密接に関わっているからです。
ここで直感的な理解のために、ボルツマン分布からのアナロジーで密度行列の固有値を$e^E$と思って議論しましょう(Li & Haldane, 2008などと類似しています)。 系が有限のエネルギーギャップを持つ場合、この仮想的な高エネルギー状態の重みは指数関数的に小さくなります。したがって、小さい固有値を切り捨てるくりこみ操作は、非常に高い精度で成立します。
しかし、系がギャップレス(臨界点近傍など)である場合はどうでしょうか。基底状態から連続的に励起状態が存在するため、固有値スペクトルはなだらかな裾野を引く形になります。この場合、ボンド次元 χ を大きくしても切り捨てられる部分の重みがなかなか小さくならず、これが精度上の課題となります。
実際、有限エンタングルメントスケーリングの理論(
Tagliacozzo et al., 2008) によれば、一般に数値計算誤差は、ギャップのある系では $\sim exp(−\chi)$ に従うのに対し、ギャップレスな系では$\sim \chi^{-\mu}$ のべき乗則に従うことが知られています。
DMRG
DMRGの基本概念
DMRG(密度行列くりこみ群)は密度行列にハミルトニアンを少しずつ作用させていきながら、その都度自由度の削減を行う手法になっています。主な使用用途としては時間発展の逐次計算や基底状態の変分最適化があり、今回は実用上重要な後者のアルゴリズムについて、一次元の量子系を舞台に見ていこうと思います。
前回量子古典対応を見たところで、鈴木トロッター分解を用いて虚時間発展を行いました。これの実時間バージョンを1ステップずつ行いながら道中で上手いくりこみを取り入れることを考えていきます。
まずは舞台となる1次元系として、5つのサイトからなる系を考えます。この系の波動関数は一般に下のように書き下せます。
\begin{equation}
|\Psi\rangle = \sum_{i_1,i_2,i_3,i_4,i_5} A_{i_1,i_2,i_3,i_4,i_5} |i_1,i_2,i_3,i_4,i_5\rangle
\end{equation}
ここで$A_{i_1,i_2,i_3,i_4,i_5}$は複素数値を持つテンソルで、$i_1,i_2,i_3,i_4,i_5$はそれぞれのサイトのスピンの値を表す外部自由度です。
今この系の波動関数をMPSの形で表現することを考えましょう。テンソルの積に分解したいので、試しに$i_1$の部分を引っ張ってきて特異値分解を行ってみると、
\begin{equation}
A_{i_1,i_2,i_3,i_4,i_5} =\sum_a B_{i_1,a} S_{a} A'_{a,i_2,i_3,i_4,i_5}
\end{equation}
となります。ここで$B_{i_1,a},A'_{a,i_2,i_3,i_4,i_5}$はユニタリ行列で、$S_{a}$は特異値行列です。
この操作を係数込みでどんどん繰り返していくと、
\begin{equation}
\begin{split}
S_{a} A'_{a,i_2,i_3,i_4,i_5} = \sum_b B'_{a,i_2,b} S'_{b} A''_{b,i_3,i_4,i_5}\\
S'_{b} A''_{b,i_3,i_4,i_5} = \sum_c B''_{b,i_3,c} S''_{c} A'''_{c,i_4,i_5}\\
S''_{c} A'''_{c,i_4,i_5} = \sum_d B'''_{c,i_4,d} S'''_{d} A''''_{d,i_5}
\end{split}
\end{equation}
となり、結果的に
\begin{equation}
\begin{split}
A_{i_1,i_2,i_3,i_4,i_5} = \sum_{a_1,a_2,a_3,a_4,a_5} B_{i_1,a} B'_{a,i_2,b} B''_{b,i_3,c} B'''_{c,i_4,d} S'''_{d} A''''_{d,i_5}
\end{split}
\end{equation}
となります。この標識を行列積波動関数(MPWF)と呼びます。これだけだと計算で何をやったのかよくわからないのでダイアグラムで書いてみましょう。
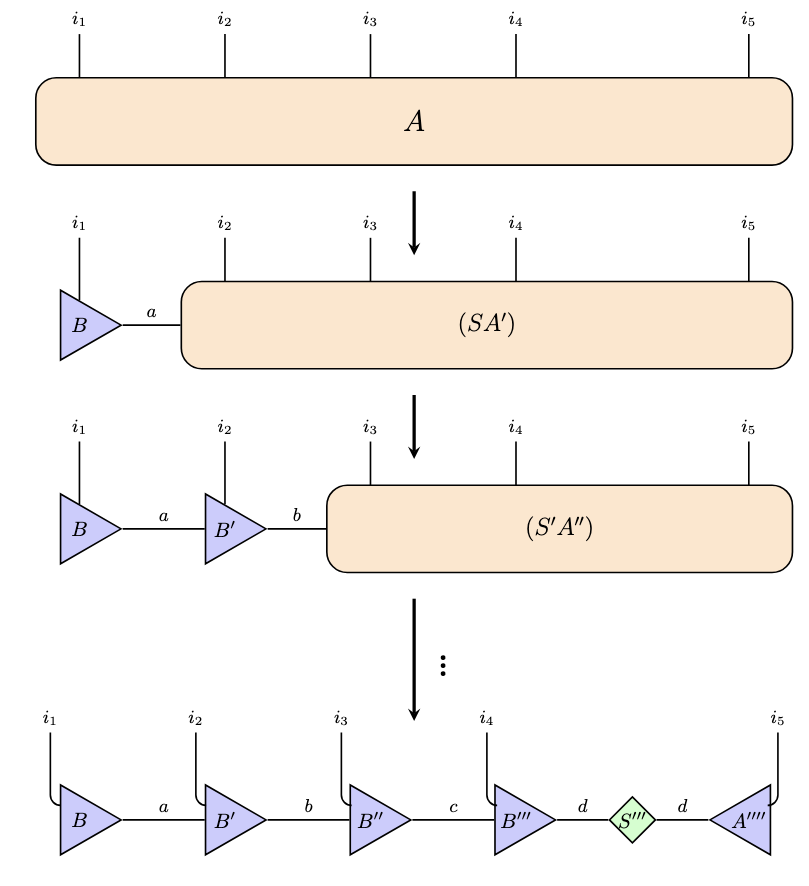 MPSの作り方
MPSの作り方
今回私たちが行いたいのは、基底状態の計算なわけですが、ここで変分法を用います。変分法はみなさんどこかで聞いたことがあると思いますが、要は毎ステップでエネルギーが小さくなる方を採用していこう!という手法です。具体的な数式で書けば、今回評価しなければならないエネルギーは、規格化定数を除いて
$E=\langle\phi|H|\phi\rangle$
になるわけですから、$E$が小さくなる方に$|\phi\rangle$をどんどん更新していけばいいでしょう。この$E=\langle\phi|H|\phi\rangle$は、さっき作ったMPSを使ってテンソルネットワークで書けば以下のようになります。
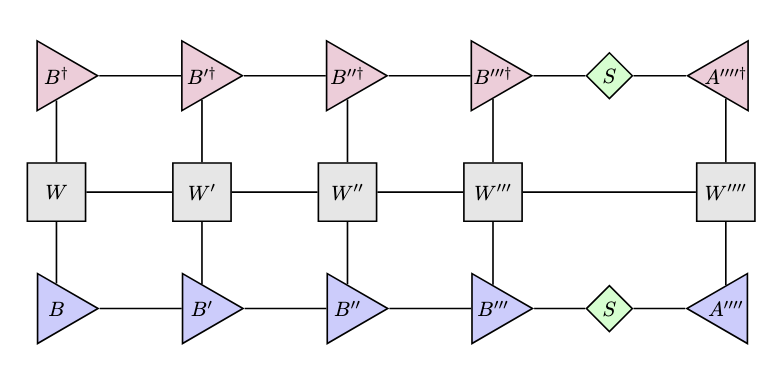 エネルギーを求めるテンソルネットワーク
エネルギーを求めるテンソルネットワーク
ここで、今回使用するランチョス法という手法について簡単に紹介しておきましょう。
初期ベクトル $|v_0\rangle$ にハミルトニアン $H$ を繰り返し作用させることでクリロフ部分空間 $\mathcal{K}_k = \mathrm{span}\{ |v_0\rangle, H|v_0\rangle, \dots, H^{k-1}|v_0\rangle \}$ を生成する。この空間の正規直交基底を用いて、巨大な $H$ を小さな三重対角行列 $T_k$ へと射影し、それを対角化することで、元の $H$ の極値固有値(特に基底エネルギーに対応する最小固有値)と固有ベクトルの非常に良い近似解を得る。
通常の対角化とは異なり、ランチョス法は行列の全要素を記憶する必要がありません。「あるベクトルにハミルトニアンを作用させるとどうなるか」という計算結果さえあれば基底状態を探索できるので、大量の要素を持った行列に対しても適用することにできます。
具体的な計算とダイアグラムのフロー
初期状態として、$\langle\phi|H|\phi\rangle$のテンソルネットワークを用意しましょう。流石にダッシュをいっぱい書いてくのも大変なので、番号を振りなおします。
$\sum_{a,b,c,d,e} B^1_{i_1,a} B^2_{a,i_2,b} B^3_{b,i_3,c} B^4_{c,i_4,d} S_{d} A^1_{d,i_5}$
また波動関数内部のアイソメトリー同士のボンド次元を、最大$\chi$に制限しておきます。
- 特異値を挟んで左右のブロックを事前計算しておき、その情報を保存しておく。これらのテンソルはせいぜい足を3本しか持たないので、メモリを圧迫する危険性はない。
 保存するテンソル一覧
保存するテンソル一覧
- 特異値とその左側の2つのアイソメトリーを一旦ダイアグラムから外す。そして中央の巨大なテンソルに対してランチョス法を用いて最低固有値(つまり最低エネルギー状態)に対応する固有ベクトルを求める。
この巨大なテンソルは足を見てみると、次元は$\chi^2 d^2$であり、行列要素は$\chi^4 d^4$になる。一般的なパラメーター$\chi=1000$などを入れると、$\chi^2 d^2$であれば問題ないが$\chi^4 d^4$は愚直に保存してしまうとメモリが爆発してしまう。ランチョス法では初期ベクトルに対する計算値のみで十分であり、このテンソルの右側と左側の要素は事前計算で求めてあるので、メモリは$\chi^2 d^2$で抑えることができるようになっている。
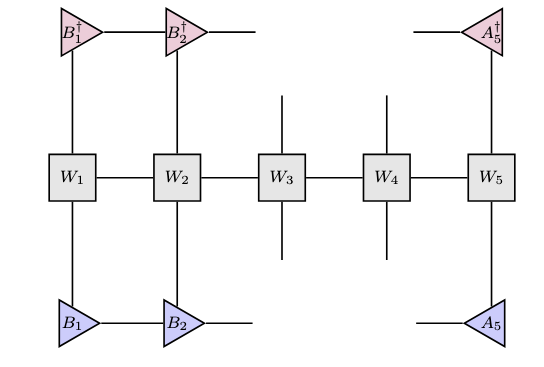 有効ハミルトニアンに該当する、欠けたテンソルネットワーク
有効ハミルトニアンに該当する、欠けたテンソルネットワーク
3. 得られた固有ベクトルを特異値分解してもう一度代入し直す。すると特異値の位置が一つ左にずれる。
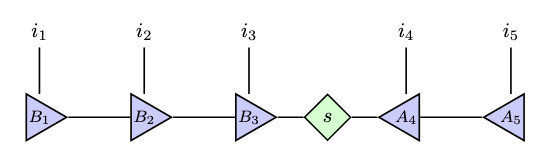 特異値がずれた後のMPS
特異値がずれた後のMPS
4. 最後に、事前計算していたテンソルのうち、新しく生成されたアイソメトリーを含むものについて更新を行う。これによって、またランチョス法の時に計算が楽になる。
5. 以上の過程を左端に到達するまで繰り返す。到達したら左右を反転し、また左端まで繰り返す。これを任意の回数だけ行う。
計算量と近似精度
計算量に関しても近似制度に関してもCTMRGとほぼ同じです。計算量は特異値分解の$ \mathcal{O}(N^3)$が結局最大の寄与なので、これを系の長さ分繰り返すことから$ \mathcal{O}(L\chi^3 d^3)$程度になります。メモリの瞬間的な最大使用量も$\mathcal{O}(L\chi^2 d^3)$程度になります。
DMRGにおいてもCTMRGとほとんど同じ理由でギャップドな系とギャップレスな系では近似精度が異なり、ギャップドな系であれば$\sim exp(-\chi)$に従い、ギャップレスな系であれば$\sim \chi^{-\mu}$に従います。
CTMRGとDMRGの関係性
今回の紹介した2つの計算手法にも、空間と時間の対応関係が如実に現れています。
CTMRGの手法が、最初から2次元の空間を用意して、ある種の実空間くりこみを行なっていくような手法だったのに対し、DMRGはハミルトニアンを2サイトずつにわたって作用させながら最適化を行なっていくという時間発展の描像であったことに気が付いたでしょうか?
巨大なテンソルと書いたところは、ある種注目する2サイトに対する有効ハミルトニアンとして作用しており、その中での局所最適化のタスクを繰り返すことで徐々に基底状態に向かっていたのでした。
これはちょうど、前回の記事で横磁場イジング模型の虚時間発展を考えた時と同じ形式になっていますね。
遊べるシミュレーション
さて、こういうテンソルネットワークの実用的な計算手法の記事には、それを実際に使って遊べるシミュレーションがつきものなのですが、ここでどう個性を出すのかが一つの勝負どころだったりします。今回はあえて、今回紹介したくりこみの手法がうまくいかない例を出してみようと思います。
以下のリンクからcloneしてもらえれば触ってもらえると思います。
https://github.com/Hirokikuwata/TensorNetwork_demo/tree/main
系自体はただの2次元イジング模型と1次元横磁場イジング模型のシミュレーションなのですが、その誤差が臨界系とそうでない系でどのように収束していくか、そのグラフを出せるようにしました。また、中身のアルゴリズムが見やすいようにPythonのnumpyしか使わずに実装しています。少し速度は遅いですが、今回紹介した内容の理解の助けになるのではないかなと思っています。
一般にテンソルネットワークを触りたければ、c++やjuliaで使用可能なITensorやPython向けでもTenPyなどのライブラリがあります。これらを使った物性系のシミュレーション等も面白いのでぜひ触ってみてください。
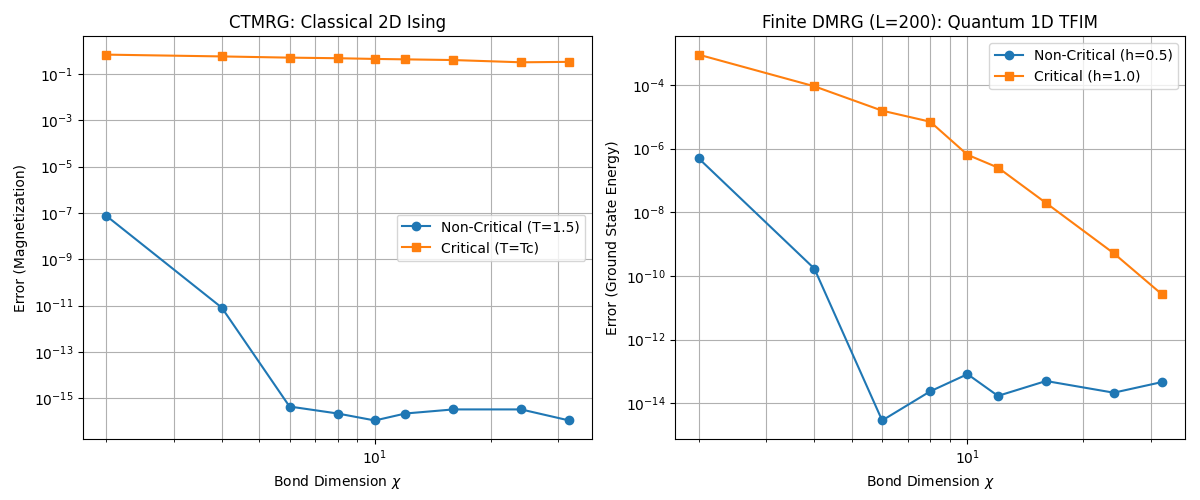 理論値に対する誤差の収束とボンド次元の関係。非臨界系だと、割とすぐに丸め誤差の所まで行ってしまうが、臨界系だと比較的ゆっくり収束する
理論値に対する誤差の収束とボンド次元の関係。非臨界系だと、割とすぐに丸め誤差の所まで行ってしまうが、臨界系だと比較的ゆっくり収束する
もう一つのくりこみ:MERA
この記事の締めくくりとして、もう一つの重要なくりこみの形である MERA(Multi-scale Entanglement Renormalization Ansatz:多尺度エンタングルメントくりこみ) について紹介したいと思います。
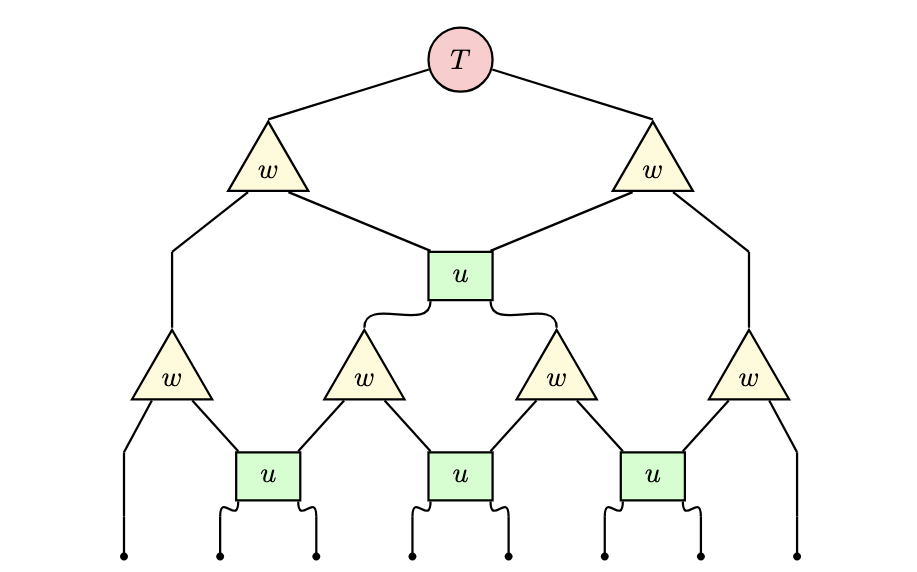 MERA
MERA
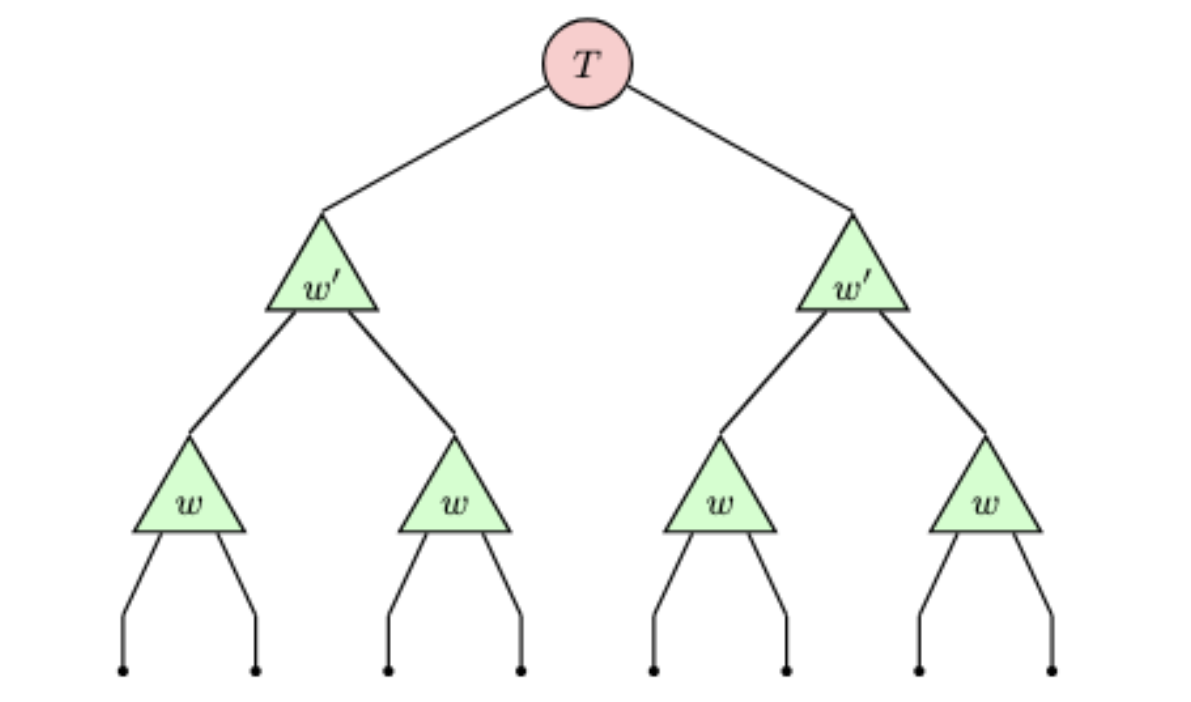
MERAのネットワーク図を見ると、三角形のテンソル w(アイソメトリー)と、四角形のテンソル u(ディスエンタングラー / disentangler)という2種類の部品で構成されていることがわかります。詳しい定義や構造は次回の記事に譲るとして、ここではなぜこの形が「くりこみ」と呼ばれるのか」、そしてなぜ「エンタングルメント」を冠しているのかという直感的な理由を見ていきましょう。
時間発展とスケール変換
前回の記事の通常の(虚)時間発展(トロッター分解)のダイアグラムでは、ユニタリ演算子を層状に積み重ねることで、物理的な時間 t を進めていきました。 一方、MERAの図を「下から上へ」見ていくとどうでしょうか。下の層ではたくさんあった足(自由度)が、アイソメトリー w を通るたびに統合され、上の層に行くほど本数が減っていくのがわかります。
 前回のダイアグラム
前回のダイアグラム
つまり、このダイアグラムにおいて「縦方向」に進むことは、物理的な時間を進めることではなく、ミクロな多数の粒子をマクロな少数の有効自由度へと集約するスケール変換に対応しているのです。
なぜディスエンタングラーが必要なのか?
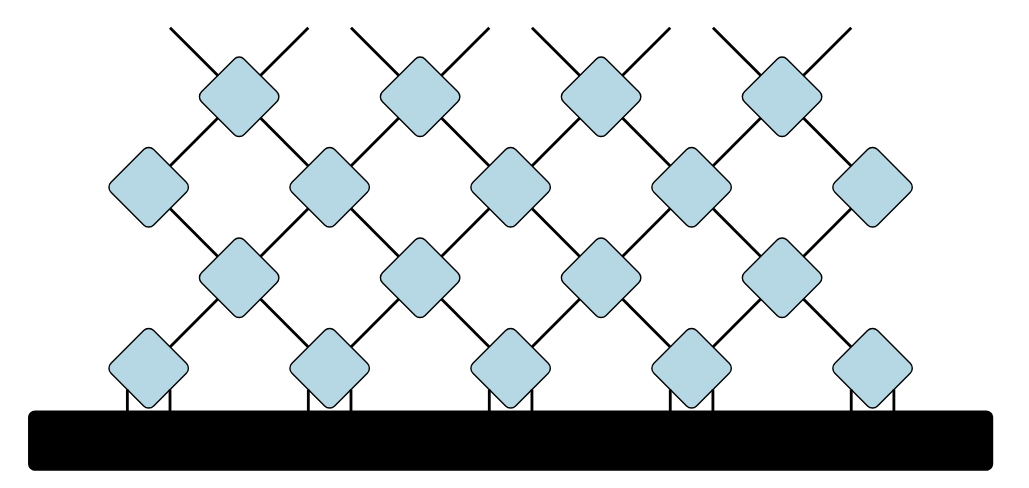
では、単に$w$で束ねていくだけ(Tree Tensor Network)ではなく、なぜわざわざ $u$(disentangler) という演算子を挟むのでしょうか? ここに、先ほどCTMRGの章で触れた「近似精度の課題」への回答があります。
 Tree Tensor Network
Tree Tensor Network
CTMRGの議論を思い出してください。ギャップのある系では精度良く計算できましたが、ギャップレスな系(臨界系)では、エンタングルメントが遠方まで広がっているため、ボンド次元を大きくしても誤差がなかなか減らない($\sim\chi^{-\mu}$)という問題がありました。 これは、単純なブロック化(粗視化)を行うだけでは、ブロックの境界付近にある短距離のエンタングルメントが除去しきれず、くりこみのステップが進むにつれてゴミのように蓄積してしまうことが原因です。
ここで登場するのが$u$(disentangler) です。 この演算子は、情報を圧縮する$w$の直前に作用し、隣り合うブロック間の短距離のもつれを局所的に解除(除去)する役割を担います。
このサイクルを繰り返すことで、MERAは上の層(マクロなスケール)に長距離のエンタングルメント(構造的な相関)だけを純粋な形で持ち上げることができます。 その結果、CTMRG等が苦手としていた臨界系であっても、MERAを用いれば驚くほど少ないボンド次元で高精度な記述が可能になるのです。
以上のことをまとめると、MERAは「エンタングルメント(もつれ)を制御しながら行うくりこみ」であるので、エンタングルメントくりこみと呼ばれているわけです。
次回に向けて
今回はテンソルネットワークの実用的な面に目を向けてきましたが、その中でもやはり、時間発展と空間拡張の対応関係が如実に生きていることが見受けられました。最後に紹介したMERAは、CTMRGやDMRG同様、アイソメトリーを用いた自由度の削減を有効活用したものになっていましたが、こちらにも同様に時間と空間の2つの解釈を持ち込むとどうなるでしょうか?その視点が次回のキーポイントとなってきます。どうぞ最後までお付き合いください。
