5
大学数学基礎解説

2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その4

代数学,入試数学
153
0
$$$$

前回の記事： 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その3
前回までは問題にあるCalkin-Wilfツリーではなく，よく似たStern-Brocotツリーの方をいじっていましたが，第4回にしてようやくCalkin-Wilfツリーの方に話題が移ります．入試において，一つの小問の回答にこんなに時間をかけていたら普通にアウトですが，これは入試ではないのでじっくり考察していきましょう．
やっぱりこの記事の内容も[Gyo20]に基づいています．

概要

だいぶ間が空いてしまったので，Calkin-Wilfツリーについて思い出しておきましょう．

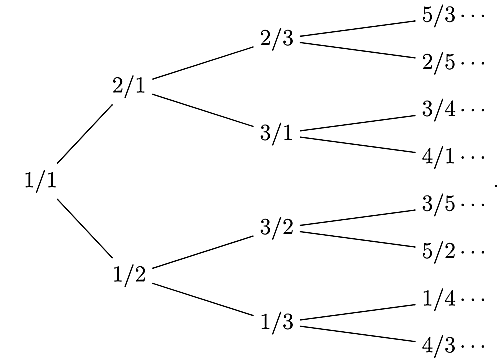
下の図のように, $\dfrac{1}{1}$から始めて分数$\dfrac{p}{q}$に$\dfrac{p}{p+q}$と$\dfrac{p+q}{q}$がつながっている樹形図を考える．
calkin-wilf calkin-wilf
このような樹形図を，Calkin-Wilfツリーという．

前回の記事で，Stern-Brocotツリーを交点ベクトルツリーから構成する方法を示しましたが，同じようにCalkin-Wilfツリーを交点ベクトルの成分を使って構成できないものでしょうか？実はできますよ，というのが今回の内容です．

初期交点ベクトルツリーとCalkin-Wilfツリー

第2回の記事 で，交点ベクトルツリーを定義したときのことを思い出してみましょう．我々は，三角形分割のフリップによって新しい辺を得るごとに，その辺の一番最初の三角形分割$L$についての交点ベクトルを樹形図の頂点に対応させていました．初期三角形分割$L$を固定して，そことの交点の様子の移り変わりを見ていたわけですね．
図でみると，
treeT3triangle treeT3triangle
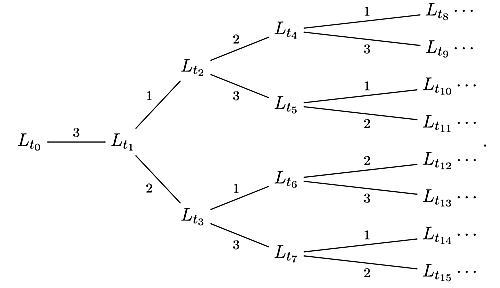
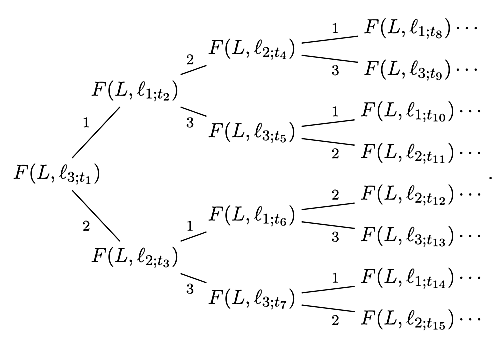
こういう風に添字づけられた三角形分割$L_{t}=(\ell_{1;t},\ell_{2;t},\ell_{3;t})$に対して，交点ベクトルを
treeintersectionvector treeintersectionvector
このように配置していたのが交点ベクトルツリーでした．
今回は固定する方を逆に辺にして，初期三角形分割の方をどんどん動かしていくツリーを考えてみましょう．ある意味，交点ベクトルツリーと双対的な樹形図を考えるわけです．
今回は初期三角形分割の左上から右斜めに走る斜線に対応する$\ell_3$を固定して，この辺と三角形分割$L_t$の交点ベクトルを計算していきましょう．
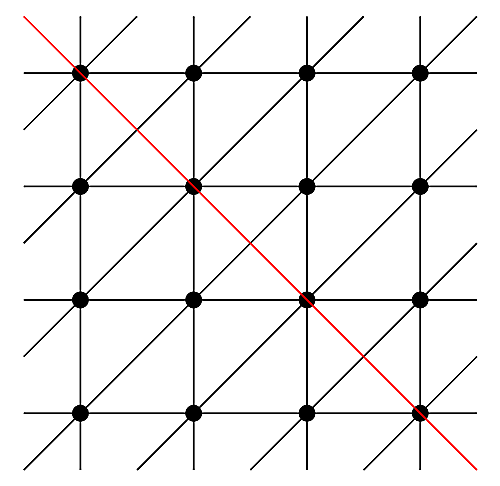
まず最初に，$L$から$\ell_3$をフリップした$L_{t_1}$との交点ベクトルを考えます．
lattice3 lattice3
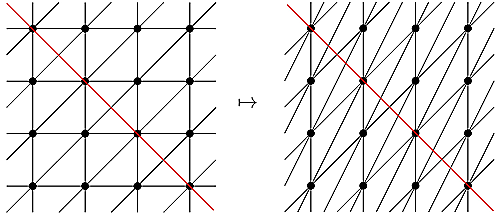
点から点までの線分がトーラスにおける辺と対応するので，$F(L_{t_1},\ell_3)=\begin{bmatrix}0\\0\\1\end{bmatrix}$となります．次に$L_{t_1}$を$\ell_1$（横線）または$\ell_2$（縦線）でフリップしてみましょう．
lattice5 lattice5
lattice4 lattice4
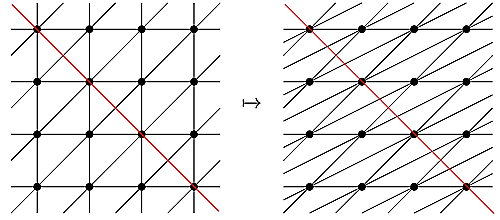
上の図が$\ell_1$,下の図が$\ell_2$をフリップしたものです．$\ell_3$とフリップした後の三角形分割$L_{t_2},L_{t_3}$についての交点ベクトルはそれぞれ
$$ F(L_{t_2},\ell_3)=\begin{bmatrix}2\\0\\1\end{bmatrix},\quad F(L_{t_3},\ell_3)=\begin{bmatrix}0\\2\\1\end{bmatrix} $$
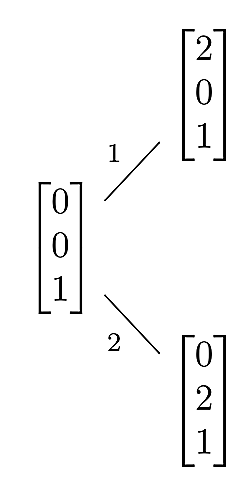
となります．これらと最初の$\begin{bmatrix}0\\0\\1\end{bmatrix}$をそれぞれフリップした辺の添字である1のラベルがついた枝，2のラベルがついた枝で結びます．こんな感じですね．
treeintersectionvector2 treeintersectionvector2
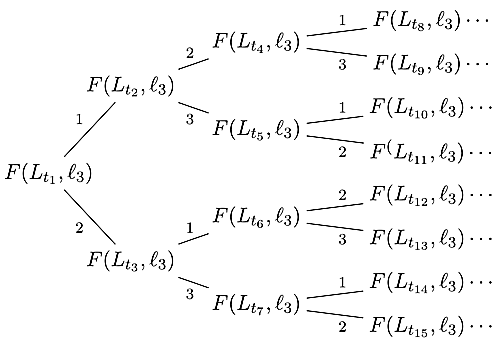
これをどんどん繰り返していきます．つまり，三角形分割をフリップして新しい三角形分割を考えるたびに,$\ell_3$についての交点ベクトルをとって樹形図の頂点に置いていく操作を続けていきます．先ほどの三角形分割の添字を使って書くとこんな感じです．
treeinitialintersectionvector treeinitialintersectionvector
最初の7つの交点ベクトルはこんな感じです．
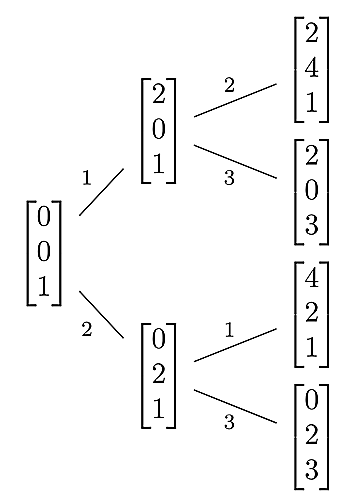initialintersectionvector2 initialintersectionvector2
これを初期交点ベクトルツリーと呼ぶことにしましょう．

初期交点ベクトルツリーとCalkin-Wilfツリーの対応

さて，交点ベクトルツリーと初期交点ベクトルツリーを比較してみることにしましょう．
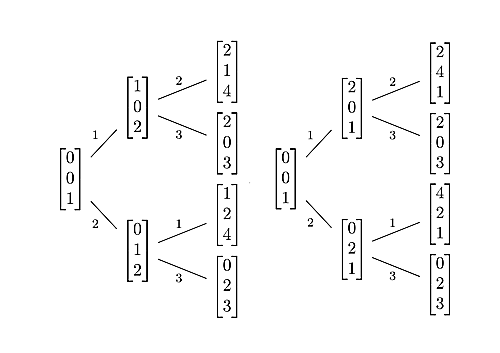compare compare
左が交点ベクトルツリー，右が初期交点ベクトルツリーです．似てるような似てないような…？なんだかStern-BrocotツリーとCalkin-Wilfツリーも似てるような似てないような感じでしたが，そんな感じの関係性に近そうな気もします．
実はこの直感はある意味で正しいんですね．そのことを示す定理を紹介しましょう．
予め，(ツリーのある頂点から)「右側，左側の頂点」という言葉をこれらは全て下図のツリーにおける右側，左側の意味で使用すると約束しておきます．
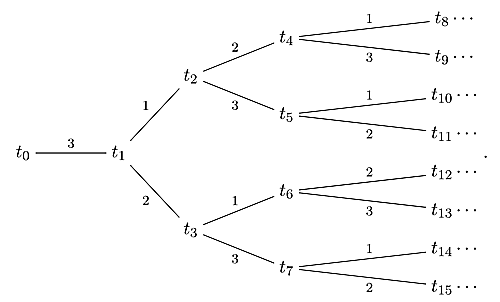treeT3 treeT3
さて，次の定理が成り立ちます．

Calkin-Wilfツリーと初期交点ベクトルツリーの対応

初期交点ベクトルツリーの頂点$F(L_t,\ell_3)=\begin{bmatrix}f_{1;t}\\f_{2;t}\\f_{3;t}\end{bmatrix}$を次のように帰納的に置き換える：

  1. 一番最初のベクトル$F(L_{t_1},\ell_3)=\begin{bmatrix}0\\0\\1\end{bmatrix}$は，(第1成分$+1$)を分子，(第2成分$+1$)を分母とする分数$\dfrac{0+1}{0+1}=\dfrac{1}{1}$に置き換える．

  2. $\{a,b,c\}=\{1,2,3\}$とする. $F(L_t,\ell_3)$が$\dfrac{f_ {a;t}+1}{f_{b;t}+1}$に置き換えられており， $F(L_t,\ell_3)$ と$F(L_{s},\ell_3)$がラベル$k$の枝で結ばれていて，$F(L_{s},\ell_3)$がツリー上$F(L_{t},\ell_3)$の右側にあるとする．このとき，$F(L_{s},\ell_3)$を，

    • $k=a$ならば，$\dfrac{f_{c;t}+1}{f_{b;t}+1}$に置き換える.
  • $k=b$ならば，$\dfrac{f_{a;t}+1}{f_{c;t}+1}$に置き換える．

この操作で得るツリーはCalkin-Wilfツリーである．

はい，操作を日本語で厳密に表現しようとして何やら複雑な感じになっちゃってますね．これが私の表現力の限界です，すいません．もっといい感じに簡潔に表現できるって人がいらっしゃったら教えてください．
ひとまず実際に構成する手順をみてもらって「あー成り立ってそうだなー」みたいなことを実感してもらえばと思います．
まず，最初に，初期交点ベクトルの最初のベクトル$\begin{bmatrix}0\\0\\1\end{bmatrix}$を，その第1成分の$0$に$1$足したものを分子に，第2成分の$0$に$1$足したものを分母に持つ分数$\dfrac{0+1}{0+1}=\dfrac{1}{1}$置き換えます．ここで，第1成分第2成分どっちも$0$じゃないかと思われるかもしれませんが，後の帰納的な定義のために必要な情報です（どっちがどっちって決まってさえいればいいので逆でも別に構わないのですが今回はこうします）．
ここで，初期交点ベクトルツリー上で，フリップする前と後の交点ベクトルはフリップしたところの成分だけが変化していることがみて取れると思います．三角形分割をフリップしたとき変化するのは1辺だけですので，ある意味これは当たり前ですね．だから，例えば$L_{t_1}=(\ell_1,\ell_2,\ell'_3)$を$\ell_1$でフリップして$L_{t_2}=(\ell''_1,\ell_2,\ell'_3)$としたとき，交点ベクトルを比較すると$\begin{bmatrix}0\\0\\1\end{bmatrix}$から$\begin{bmatrix}2\\0\\1\end{bmatrix}$になり，第1成分だけが変わっています．そこで，対応する分数の方は，$\dfrac{\text{第1成分}+1}{\text{第2成分}+1}$だった$\dfrac{1}{1}$から，変化していない第2成分を残して，使われていなかった第3成分を第1成分の代わりに用いて$\dfrac{\text{第3成分}+1}{\text{第2成分}+1}=\dfrac{1+1}{0+1}=\dfrac{2}{1}$へ移るとします．（第2成分と第3成分は変化前変化後どちらでも同じであることに注意してください）．
$\ell_2$をフリップする場合，$\begin{bmatrix}0\\0\\1\end{bmatrix}$から$\begin{bmatrix}0\\2\\1\end{bmatrix}$になり，第2成分だけが変わっています．同様に，変化しない第1成分をそのまま残し，使われていなかった第3成分を変化してしまった第2成分の代わりに用いて分数を構成します．$\dfrac{\text{第1成分}+1}{\text{第3成分}+1}=\dfrac{0+1}{1+1}=\dfrac{1}{2}$となり，これが$\begin{bmatrix}2\\0\\1\end{bmatrix}$から置き換えられる分数であると定めるわけですね．この手順で分数を置き換えていくと，最初の7つは次のようになります．
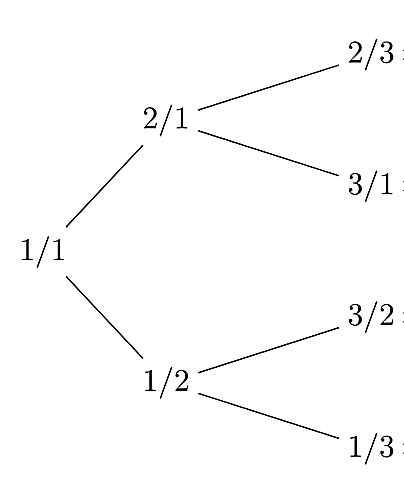calkin-wilfsub calkin-wilfsub
確かにCalkin-Wilfツリーになっていることが見て取れると思います．

さて，この構成方法，実はStern-Brocotツリーと全く対になるような方法なんですね．交点ベクトルツリーは辺を変化させて導出している一方，初期交点ベクトルツリーは辺を固定して計算しています．また，Stern-Brocotツリーを交点ベクトルツリーから構成するときに取り出すベクトルの成分は常に第1成分と第2成分で固定ですが，Calkin-Wilfツリーは取り出すベクトルの成分がフリップするごとに変化しています．

ここで興味深いのは，Stern-BrocotツリーとCalkin-Wilfツリーという定義に関連性の見えない2つのツリーが，1点付きトーラスの三角形分割という共通のツールから全く対称的な方法で取り出されるという事実です．

これは個々のツリーを眺めているだけでは到底発見できない事実です．また，初等的な整数問題という枠組みの中で考えていてもたどり着くことは難しいと思います．実は，この1点トーラスの三角形分割の背景にはクラスター代数というある代数構造が隠れており，これを知っているとこの構造に気づくことができます．クラスター代数は20年前に見出された新しい代数構造であり，現在も世界中の数学者が様々な応用を続々と見つけているまさに発展途上の分野です．このように，大学の数学を学ぶと高校までやってきた数学に対しても新しい視点を得られる場合がありますので，高校までの数学が好きな方も，大学の数学に取り組んでみると新しい発見があって面白いかもしれません！

さて，余談がちょっとすぎましたね．今回はもうくたびれたのでここらへんでおしまいにして，次回は定理1の証明をやっていきたいと思います．実は，定理1が示せてしまえば頂点の分数の既約性はStern-Brocot側の分数の既約性からすぐに導出できることがわかります．ということで後もう少し，自分の情熱が冷めないうちにこのシリーズを完結させたいところであります．今回も読んでいただきありがとうございました．

次の記事： 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その5

参考文献

  • [Gyo20] Y. Gyoda, Cluster duality between Calkin-Wilf tree and Stern-Brocot tree, 2020. preprint, arXiv:2009.06473 [math.NT]
投稿日：2020年11月17日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

rodin_math
155
24718

コメント

他の人のコメント

コメントはありません。
読み込み中
rodin_math
2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その4