大学数学基礎解説

2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解くその5

代数学,入試数学

128

前回の記事： 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解くその4

概要

今回は次の定理を示していきます．

Calkin-Wilfツリーと初期交点ベクトルツリーの対応

初期交点ベクトルツリーの頂点 $F (L_{t}, ℓ_{3}) = [\begin{matrix} f_{1; t} \\ f_{2; t} \\ f_{3; t} \end{matrix}]$ を次のように帰納的に置き換える：

一番最初のベクトル $F (L_{t_{1}}, ℓ_{3}) = [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}]$ は，(第1成分 $+ 1$ )を分子，(第2成分 $+ 1$ )を分母とする分数 $\frac{0 + 1}{0 + 1} = \frac{1}{1}$ に置き換える．
${a, b, c} = {1, 2, 3}$ とする. $F (L_{t}, ℓ_{3})$ が $\frac{f_{a; t} + 1}{f_{b; t} + 1}$ に置き換えられており， $F (L_{t}, ℓ_{3})$ と $F (L_{s}, ℓ_{3})$ がラベル $k$ の枝で結ばれていて， $F (L_{s}, ℓ_{3})$ がツリー上 $F (L_{t}, ℓ_{3})$ の右側にあるとする．このとき， $F (L_{s}, ℓ_{3})$ を，
- $k = a$ ならば， $\frac{f_{c; t} + 1}{f_{b; t} + 1}$ に置き換える.

$k = b$ ならば， $\frac{f_{a; t} + 1}{f_{c; t} + 1}$ に置き換える．

この操作で得るツリーはCalkin-Wilfツリーである．

この操作が具体的にどういうことを行っているのかについては前回の記事に書いてあるのでそちらをどうぞ．
この記事の内容は[Gyo20]に…もう聞き飽きましたね．

交点行列とその具体的な記述

定理を証明するための準備として，交点ベクトルを横に並べた交点行列を導入しましょう．

交点行列

$L = (ℓ_{1}, ℓ_{2}, ℓ_{3}), M = (m_{1}, m_{2}, m_{3})$ を1点付きトーラス上の三角形分割として， $f_{i j}$ を $ℓ_{i}$ と $m_{j}$ のトーラス上での交差回数とする（ただしトーラスについている1点上での交差を含めない）．
このとき， $L$ と $M$ の交点行列 $F (L, M)$ を次で定義する:
$F (L, M) = (F (L, m_{1}), F (L, m_{2}), F (L, m_{3})) = [\begin{matrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{matrix}] .$

要はこれまでの交点ベクトルを横に並べて行列にしたものですね．まず，この交点行列が三角形分割 $L$ を固定して $M$ をフリップしたときにどういう値の動き方をするのかを見てみましょう．ただし， $M$ は $T_{3}^{'}$ の頂点に対応する三角形分割を考えます．ここで， $T_{3}^{'}$ は $t_{0}$ を経由せずに $t_{1}$ へたどり着けるような $T_{3}$ の頂点全体からなる $T_{3}$ の部分木 $T_{3}^{'}$ です．下の図から $t_{0}$ と $t_{0}$ から $t_{1}$ につながる枝を取り除いたものです．
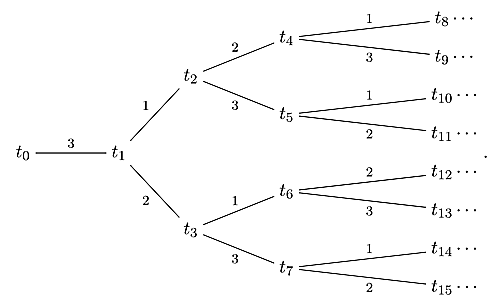treeT3 treeT3
過去の記事で証明したいくつかの事実を使用します．例によって $L = (ℓ_{1}, ℓ_{2}, ℓ_{3})$ を一つ固定しておきます．三角形分割の辺 $ℓ$ の傾き ${grad}_{L} (ℓ)$ の定義については第3回の記事をご覧ください．

第3回の補題3

$M = (m_{1}, m_{2}, m_{3})$ を三角形分割， ${i, j, k} = {1, 2, 3}$ とする．このとき，次の2つの条件は同値である．

次のどちらかの不等式が成立する．
$\begin{array}{r} {grad}_{L} (m_{i}) < {grad}_{L} (m_{j}) < {grad}_{L} (m_{k}) or {grad}_{L} (m_{k}) < {grad}_{L} (m_{j}) < {grad}_{L} (m_{i}) . \end{array}$
$\frac{a}{b}$ と $\frac{c}{d}$ が既約分数で， ${grad}_{L} (m_{i}) = \frac{a}{b}, {grad}_{L} (m_{k}) = \frac{c}{d}$ であるとき， ${grad}_{L} (m_{j}) = \frac{a + c}{b + d}$ である．

特に，任意の三角形分割 $M = (m_{1}, m_{2}, m_{3})$ に対して $a, c \in Z$ と $b, d \in Z_{\geq 0}$ が存在して， $\frac{a}{b}$ と $\frac{c}{d}$ が既約分数であって
${{grad}_{L} (m_{1}), {grad}_{L} (m_{2}), {grad}_{L} (m_{3})} = {\frac{a}{b}, \frac{c}{d}, \frac{a + c}{b + d}}$
となる．

第3回の定理8

$ℓ \in L_{t}$ を $t \in T_{3}^{'}$ , $F (L, ℓ) \neq 0$ を満たす三角形分割 $L_{t}$ の辺とする．このとき， ${grad}_{L} (ℓ) = \frac{a}{b}$ （ただし $\frac{a}{b}$ は既約分数)であることと $F (L, ℓ) = [\begin{matrix} a - 1 \\ b - 1 \\ a + b - 1 \end{matrix}]$ であることは同値である．

どちらも証明は第3回の記事を参照してください．

これを用いると，以下の事実が示されます．

$t \in T_{3}^{'}$ として， $L_{t} = (ℓ_{1; t}, ℓ_{2; t}, ℓ_{3; t})$ を三角形分割とする．任意の $i \in {1, 2, 3}$ に対して， $F (L, ℓ_{i; t}) \neq 0$ であるとき， $F (L, L_{t}) = (f_{i j})$ は次のどれかである．

( $i$ ) $[\begin{matrix} f_{11} & f_{12} & f_{11} + f_{12} + 1 \\ f_{21} & f_{22} & f_{21} + f_{22} + 1 \\ f_{11} + f_{21} + 1 & f_{12} + f_{22} + 1 & f_{11} + f_{12} + f_{21} + f_{22} + 3 \end{matrix}]$

( $ii$ ) $[\begin{matrix} f_{12} + f_{13} + 1 & f_{12} & f_{13} \\ f_{22} + f_{23} + 1 & f_{22} & f_{23} \\ f_{12} + f_{13} + f_{22} + f_{23} + 3 & f_{12} + f_{22} + 1 & f_{13} + f_{23} + 1 \end{matrix}]$

( $iii$ ) $[\begin{matrix} f_{11} & f_{11} + f_{13} + 1 & f_{13} \\ f_{21} & f_{21} + f_{23} + 1 & f_{23} \\ f_{11} + f_{21} + 1 & f_{11} + f_{21} + f_{13} + f_{23} + 3 & f_{13} + f_{23} + 1 \end{matrix}]$

補題2，定理3から明らか．

補題4では $F (L, ℓ_{i; t}) = 0$ の場合が含まれていまぜんので， $F (L, ℓ_{i; t}) = 0$ の場合を含めた場合を考えましょう．

あらかじめ，必要な命題を用意しておきます．これも第3回で証明した命題です．

第3回の命題5

$M = (m_{1}, m_{2}, m_{3})$ を三角形分割， ${i, j, k} = {1, 2, 3}$ とする.
$\begin{array}{r} {grad}_{L} (m_{i}) < {grad}_{L} (m_{j}) < {grad}_{L} (m_{k}) \end{array}$
を仮定する．

$M^{'} = {m_{i}, m_{j}^{'}, m_{k}}$ を， $M$ を $m_{j}$ でフリップした三角形分割とする．このとき，次のどちらかの不等式が成立する．
$\begin{array}{r} {grad}_{L} (m_{j}^{'}) < {grad}_{L} (m_{i}) < {grad}_{L} (m_{k}) or {grad}_{L} (m_{i}) < {grad}_{L} (m_{k}) < {grad}_{L} (m_{j}^{'}) . \end{array}$
$M^{″} = {m_{i}^{″}, m_{j}, m_{k}}$ を， $M$ を $m_{i}$ でフリップした三角形分割とする．このとき，このとき，次の不等式が成立する．
$\begin{array}{r} {grad}_{L} (m_{j}) < {grad}_{L} (m_{i}^{″}) < {grad}_{L} (m_{k}) . \end{array}$
$M^{‴} = {m_{i}, m_{j}, m_{k}^{‴}}$ を， $L_{t}$ を $m_{k}$ でフリップした三角形分割とする．このとき，次の不等式が成立する．
$\begin{array}{r} {grad}_{L} (m_{i}) < {grad}_{L} (m_{k}^{‴}) < {grad}_{L} (m_{j}) . \end{array}$

証明は第3回の記事を参照してください．
さて，次の定理が交点行列の記述を与える定理になります．多分この定理がこのシリーズの中で一番非自明な定理だと思います．なお， $L_{t}$ を $k$ 番目の辺でフリップした三角形分割を $φ_{k} (L_{t})$ で表すものとします．

$t \in T_{3}^{'}$ として， $L_{t} = (ℓ_{1; t}, ℓ_{2; t}, ℓ_{3; t})$ を三角形分割とする． $F (L, L_{t}) = (f_{i j})$ は次のどれかである．

( $i$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}]$

( $ii$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & f_{22} & f_{22} + 1 \\ 0 & f_{22} + 1 & f_{22} + 2 \end{matrix}]$

( $iii$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & f_{23} + 1 & f_{23} \\ 0 & f_{23} + 2 & f_{23} + 1 \end{matrix}]$

( $iv$ ) $[\begin{matrix} f_{11} & 0 & f_{11} + 1 \\ 0 & 0 & 0 \\ f_{11} + 1 & 0 & f_{11} + 2 \end{matrix}]$

( $v$ ) $[\begin{matrix} f_{13} + 1 & 0 & f_{13} \\ 0 & 0 & 0 \\ f_{13} + 2 & 0 & f_{13} + 1 \end{matrix}]$

( $vi$ ) $[\begin{matrix} f_{11} & f_{12} & f_{11} + f_{12} + 1 \\ f_{21} & f_{22} & f_{21} + f_{22} + 1 \\ f_{11} + f_{21} + 1 & f_{12} + f_{22} + 1 & f_{11} + f_{12} + f_{21} + f_{22} + 3 \end{matrix}]$

( $vii$ ) $[\begin{matrix} f_{12} + f_{13} + 1 & f_{12} & f_{13} \\ f_{22} + f_{23} + 1 & f_{22} & f_{23} \\ f_{12} + f_{13} + f_{22} + f_{23} + 3 & f_{12} + f_{22} + 1 & f_{13} + f_{23} + 1 \end{matrix}]$

( $viii$ ) $[\begin{matrix} f_{11} & f_{11} + f_{13} + 1 & f_{13} \\ f_{21} & f_{21} + f_{23} + 1 & f_{23} \\ f_{11} + f_{21} + 1 & f_{11} + f_{21} + f_{13} + f_{23} + 3 & f_{13} + f_{23} + 1 \end{matrix}]$

加えて，次の図式が成立する．
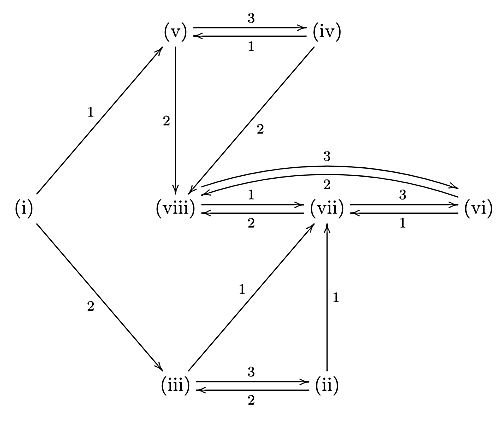diagram diagram
ただし， $(n) \overset{k}{⟶} (m)$ は $F (L, L_{t})$ が $(n)$ を満たすとき $F (L, φ_{k} (L_{t}))$ が $(m)$ を満たすことを意味している．

フリップを同じ位置で2回続けて行うと元に戻ることに注意すると, 定理中の図式に現れるフリップだけを調べれば十分であることがわかる． $t = t_{1}$ のとき $F (L, L_{t})$ は( $i$ )を満たすので，以下帰納的に図式中の矢印が正しいことを示す．
最初に，( $vi$ )から( $viii$ )の間の矢印について確かめる．( $vi$ )から( $viii$ )の間の図式でのフリップを考えると，フリップした後の入れ替わった辺の傾きは定理3と命題5から真ん中の大きさである．よって，これらの間の矢印については補題4から正しいことがわかる．
次に( $ii$ ) と( $iii$ )の間の矢印について確かめる． $F (L, L_{t})$ が( $ii$ )または( $iii$ )を満たすことを仮定したとき， ${grad}_{L} (ℓ_{1; t}) = 0$ かつ $(ii) \overset{2}{⟶} (iii)$ または $(iii) \overset{3}{⟶} (ii)$ であることを帰納的に確かめれば十分である．まず最初に $F (L, L_{t}) = F (L, φ_{2} (L_{t_{1}}))$ ならば， $F (L, L_{t})$ は $(iii)$ を満たし， ${grad}_{L} (ℓ_{1; t}) = 0$ である．仮定のもとで $F (L, L_{t})$ が $(ii)$ を満たすならば定理3より ${grad}_{L} (ℓ_{1; t}) < {grad}_{L} (ℓ_{3 : t}) < {grad}_{L} (ℓ_{2; t})$ であることがわかる．したがって，補題2，定理3，命題5から $(ii) \overset{2}{⟶} (iii)$ が示される． $L_{t^{'}} := φ_{2} (L_{t})$ としたとき， $ℓ_{1; t} = ℓ_{1; t^{'}}$ であるから， ${grad}_{L} (ℓ_{1; t^{'}}) = 0$ である． $F (L, L_{t})$ が( $iii$ )を満たすときも，同様の議論から $(iii) \overset{3}{⟶} (ii)$ と ${grad}_{L} (ℓ_{1; t^{″}}) = 0$ が示される（ $L_{t^{″}} := φ_{3} (L_{t})$ とした）．
次に， $(iii) \overset{1}{⟶} (vii)$ と $(ii) \overset{1}{⟶} (vii)$ も ${grad}_{L} (ℓ_{1; t}) = 0$ と補題2，命題3，定理5から従う．
( $iv$ ),( $v$ ),( $viii$ )の間の矢印に関しては( $ii$ ),( $iii$ ),( $vii$ )の間の矢印と同様の議論をすればよい（ただし ${grad}_{L} (ℓ_{1; t}) = 0$ の代わりに ${grad}_{L} (ℓ_{2; t}) = \infty$ を用いる）．
以上のことから，( $i$ )を満たす状態から定理中の図式にあるようなフリップを行うと2度と( $i$ )を満たす状態には戻ってこないことがわかり， $(i) \overset{1}{⟶} (iii)$ と $(i) \overset{2}{⟶} (v)$ が従う．

さて，これで $F (L, L_{t})$ について後ろの $L_{t}$ をフリップをすることによってどのように変化するのかが完全にわかりました．しかし，初期交点ベクトルツリーは $ℓ_{3}$ を固定して初期三角形分割をフリップでずらすことで得られるので，我々が求めているのは $F (L_{t}, L)$ の前の $L_{t}$ をフリップで移したときの変化です．これについては次の補題が問題を簡単にしてくれます．

任意の $t \in T_{3}$ に対して，次の等式が成立する．
$\begin{array}{r} F (L_{t}, L) = (F (L, L_{t}))^{T}, \end{array}$
ただし， $T$ は転置を表す．

証明は明らかなので省略します．

次の定理は定理6の後ろではなく前の三角形分割をフリップで移すバージョンです．

$t \in T_{3}^{'}$ として， $L_{t} = (ℓ_{1; t}, ℓ_{2; t}, ℓ_{3; t})$ を三角形分割とする． $F (L_{t}, L) = (f_{i j})$ は次のどれかである．

( $i$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}]$

( $ii$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & f_{22} & f_{22} + 1 \\ 0 & f_{22} + 1 & f_{22} + 2 \end{matrix}]$

( $iii$ ) $[\begin{matrix} 0 & 0 & 0 \\ 0 & f_{32} + 1 & f_{32} + 2 \\ 0 & f_{32} & f_{32} + 1 \end{matrix}]$

( $iv$ ) $[\begin{matrix} f_{11} & 0 & f_{11} + 1 \\ 0 & 0 & 0 \\ f_{11} + 1 & 0 & f_{11} + 2 \end{matrix}]$

( $v$ ) $[\begin{matrix} f_{31} + 1 & 0 & f_{31} + 2 \\ 0 & 0 & 0 \\ f_{31} & 0 & f_{31} + 1 \end{matrix}]$

( $vii$ ) $[\begin{matrix} f_{21} + f_{31} + 1 & f_{22} + f_{32} + 1 & f_{21} + f_{31} + f_{22} + f_{32} + 3 \\ f_{21} & f_{22} & f_{21} + f_{22} + 1 \\ f_{31} & f_{32} & f_{31} + f_{32} + 1 \end{matrix}]$

( $viii$ ) $[\begin{matrix} f_{11} & f_{12} & f_{11} + f_{12} + 1 \\ f_{11} + f_{31} + 1 & f_{12} + f_{32} + 1 & f_{11} + f_{12} + f_{31} + f_{32} + 3 \\ f_{31} & f_{32} & f_{31} + f_{32} + 1 \end{matrix}]$

加えて，次の図式が成立する．
diagram diagram
ただし， $(n) \overset{k}{⟶} (m)$ は $F (L_{t}, L)$ が $(n)$ を満たすとき $F (φ_{k} (L_{t}), L)$ が $(m)$ を満たすことを意味している．

定理6と補題7から従う．

定理1の証明

さて，定理1を示していきましょう．
あまりにもわかりにくい定理なので再掲しておきます．

再掲

初期交点ベクトルツリーの頂点 $F (L_{t}, ℓ_{3}) = [\begin{matrix} f_{1; t} \\ f_{2; t} \\ f_{3; t} \end{matrix}]$ を次のように帰納的に置き換える：

一番最初のベクトル $F (L_{t_{1}}, ℓ_{3}) = [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}]$ は，(第1成分 $+ 1$ )を分子，(第2成分 $+ 1$ )を分母とする分数 $\frac{0 + 1}{0 + 1} = \frac{1}{1}$ に置き換える．
${a, b, c} = {1, 2, 3}$ とする. $F (L_{t}, ℓ_{3})$ が $\frac{f_{a; t} + 1}{f_{b; t} + 1}$ に置き換えられており， $F (L_{t}, ℓ_{3})$ と $F (L_{s}, ℓ_{3})$ がラベル $k$ の枝で結ばれていて， $F (L_{s}, ℓ_{3})$ がツリー上 $F (L_{t}, ℓ_{3})$ の右側にあるとする．このとき， $F (L_{s}, ℓ_{3})$ を，
- $k = a$ ならば， $\frac{f_{c; t} + 1}{f_{b; t} + 1}$ に置き換える.

$k = b$ ならば， $\frac{f_{a; t} + 1}{f_{c; t} + 1}$ に置き換える．

この操作で得るツリーはCalkin-Wilfツリーである．

初期交点ベクトルツリーは次のようなツリーでした．
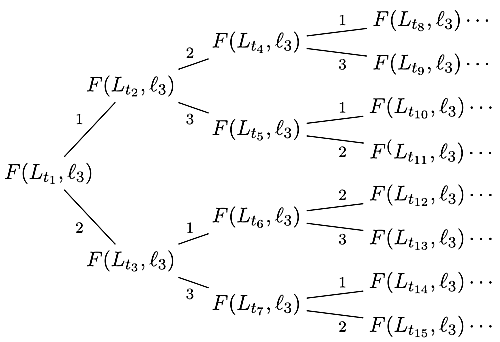treeinitialintersectionvector
今，定理8から $F (L_{t}, L)$ の前の三角形分割をフリップしたときにどういう変化をするかは完全に記述できているので，これを第3列目のベクトル $F (L_{t}, ℓ_{3})$ に限って考え，定理にあるような成分の取り出し方がCalkin-Wilfツリーと一致するかどうかを確かめればOKです．あとは帰納法による作業を残すのみです．
$q_{n}$ で分数 $q$ の分子， $q_{d}$ で分数 $q$ の分母を表すこととし， $h (F (L_{t}, ℓ_{3}))$ で $F (L_{t}, ℓ_{3})$ を定理中の操作で置き換えた分数を表すとします．

$F (L_{t}, L) = (f_{i j; t})$ と表すとすると，定理1(定理9)中の $f_{i; t}$ は $f_{i 3; t}$ を指す．以後， $f_{i j; t}$ の記号の方で議論を行う．
定理8の図式中の任意の( $n$ )と( $n$ )を満たす $F (L_{t}, ℓ_{3})$ について，
$\begin{array}{r} h (F (L_{t}, ℓ_{3}))_{n} = x h (F (L_{t}, ℓ_{3}))_{d} = y, \end{array}$
であるとき，
$\begin{aligned} h (F (φ_{a} (L_{t}), ℓ_{3}))_{n} = x + y, h (F (φ_{a} (L_{t}), ℓ_{3}))_{d} = y, \\ h (F (φ_{b} (L_{t}), ℓ_{3}))_{n} = x, h (F (φ_{b} (L_{t}), ℓ_{3}))_{d} = x + y \end{aligned}$
を満たすことを確かめれば良い．
$F (L_{t}, ℓ_{3})$ が( $i$ )を満たすときは，直接計算で求めれば良い． $F (L_{t}, ℓ_{3})$ が( $iii$ )を満たすとする．このとき，
$\begin{array}{r} h (F (L_{t}, ℓ_{3})) = \frac{f_{13; t_{1}} + 1}{f_{33; t} + 1} = \frac{1}{f_{33; t} + 1} = \frac{1}{f_{32; t} + 2} \end{array}$
であることが定理8からわかっている（分子が第1成分であることは帰納的に示される）．
定理8と $h$ の定義から， $L_{t^{'}} := φ_{3} (L_{t})$ に対して，
$\begin{aligned} h (F (L_{t^{'}}, ℓ_{3})) & = \frac{1}{f_{23; t} + 1} = \frac{1}{f_{32; t} + 3} = \frac{1}{(f_{32; t} + 2) + 1} . \end{aligned}$
一方， $L_{t^{″}} := φ_{2} (L_{t})$ に対しては
$\begin{aligned} h (F (L_{t^{″}}, ℓ_{3})) = \frac{f_{23; t} + 1}{f_{33; t} + 1} = \frac{f_{32 : t} + 3}{f_{32; t} + 2} = \frac{(f_{32 : t} + 2) + 1}{f_{32; t} + 2} \end{aligned}$
を得る．したがって $F (L_{t}, ℓ_{3})$ が( $iii$ )を満たすときは求めるべき条件を満たしている．
次に $F (L_{t}, ℓ_{3})$ が( $ii$ )を満たすとする．このとき，
$\begin{aligned} h (F (L_{t}, ℓ_{3})) & = \frac{f_{33; t_{1}} + 1}{f_{23; t} + 1} = \frac{1}{f_{23; t} + 1} = \frac{1}{f_{22; t} + 2} \end{aligned}$
が定理8からわかっている（分子が第1成分であることは帰納的に示される）．
よって定理8と $h$ の定義から， $L_{t^{'}} := φ_{2} (L_{t})$ と $L_{t^{″}} := φ_{1} (L_{t})$ に対して，
$\begin{aligned} h (F (L_{t^{'}}, ℓ_{3})) & = \frac{1}{f_{33; t} + 1} = \frac{1}{f_{22; t} + 3} = \frac{1}{(f_{22; t} + 2) + 1}, \\ h (F (L_{t^{″}}, ℓ_{3})) & = \frac{f_{33; t} + 1}{f_{23; t} + 1} = \frac{f_{22 : t} + 3}{f_{22; t} + 2} = \frac{(f_{22 : t} + 2) + 1}{f_{22; t} + 2} . \end{aligned}$
したがって $F (L_{t}, ℓ_{3})$ が( $ii$ )を満たすときは求めるべき条件を満たしている．
( $iv$ )と( $v$ )を満たす場合については( $iii$ )と( $ii$ )の場合と同様にして示される．
次に， $F (L_{t}, ℓ_{3})$ が( $vi$ )を満たす場合を考える．まず
$\begin{array}{r} h (F (L_{t}, ℓ_{3})) = \frac{f_{13; t} + 1}{f_{23; t} + 1} \end{array}$
の場合を仮定する．まず定理8から
$\begin{aligned} h (F (L_{t}, ℓ_{3})) & = \frac{f_{13; t} + 1}{f_{23; t} + 1} = \frac{f_{11; t} + f_{12; t} + 2}{f_{21; t} + f_{22; t} + 2} \end{aligned}$
であって，定理8と $h$ の定義から $L_{t^{'}} := φ_{1} (L_{t})$ と $L_{t^{″}} := φ_{2} (L_{t})$ に対して，
$\begin{aligned} h (F (L_{t^{'}}, ℓ_{3})) & = \frac{f_{33; t} + 1}{f_{23; t} + 1} = \frac{f_{11; t} + f_{12; t} + f_{21; t} + f_{22; t} + 4}{f_{21; t} + f_{22; t} + 2} \\ = \frac{(f_{11; t} + f_{12; t} + 2) + (f_{21; t} + f_{22; t} + 2)}{f_{21; t} + f_{22; t} + 2}, \\ h (F (L_{t^{″}}, ℓ_{3})) & = \frac{f_{13; t} + 1}{f_{33; t} + 1} = \frac{f_{11; t} + f_{12; t} + 2}{f_{11; t} + f_{12; t} + f_{21; t} + f_{22; t} + 4} \\ = \frac{f_{11; t} + f_{12; t} + 2}{(f_{11; t} + f_{12; t} + 2) + (f_{21; t} + f_{22; t} + 2)} . \end{aligned}$
よって求めるべき条件を満たしている．
次に
$\begin{array}{r} h (F (L_{t}, ℓ_{3})) = \frac{f_{23; t} + 1}{f_{13; t} + 1}, \end{array}$
を仮定すると，これは最初のケースと同様に求めるべき条件を満たしていることがわかる．
よって, $F (L_{t}, ℓ_{3})$ が( $vi$ )を満たすときも示された．
$F (L_{t}, ℓ_{3})$ が( $vii$ )や( $viii$ )を満たす場合も $(vi)$ の時と同じようにして示される．

これで定理1が示されました．定理6のステートメントを思いつくのが大変ですが，そこを越えてしまえば最後はもうほとんど流れ作業です．さて，これでStern-BrocotツリーとCalkin-Wilfツリーが双対的に構成されることがわかったので，あとはCalkin-Wilfツリーの分数の既約性を示すだけです．今回はもう疲れたので次回に回したいと思います．ここまで読んでくださりありがとうございました．

次の記事 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解くその6（完結）