2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その6（完結）
前回の記事： 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解く その5
今回で完結となります．結局[Gyo20]に出てくる命題をこのシリーズの中で全部証明し切ってしまいました．ここまで読んでくださった方はもうこの論文は読む必要ないです（断言）．
概要
いよいよ最終目標である以下の定理を示します．
Calkin-Wilfツリーの頂点の分数は全て既約分数である．
やっと来たかと思うと感慨深いですね．多くても10行程度の証明で済むはずのこの定理の証明を，わざわざ（比較的）難解な証明を経由して示そうとしているのですから，ここまで読んでくださった方は相当なガッツがあると思います（自分で書いておいて何なんですが，ここまでの全部の議論をフォローしてくださっている人はいらっしゃるのだろうか…）．全てをフォローしてくださっている方にもそうでない方にも，とにかく読者の皆様には本当に感謝しかありません．
定理1の証明
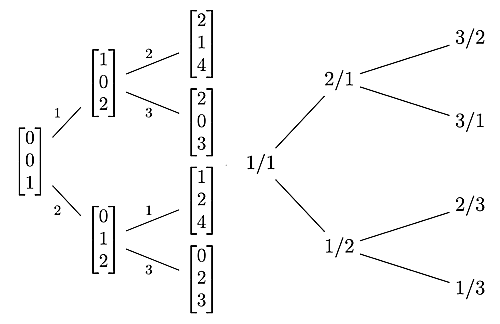
前回，初期交点ベクトルツリーからCalkin-Wilfツリーを構成したわけですが，何か気づくことはないでしょうか．実際に最初の7つの対応を並べてみましょう．
compare2
Calkin-Wilfツリーは初期交点ツリーの3つの成分のうち2つを抜き出してそれぞれ+1して分子と分母に配置するという形で構成されていましたが，どの頂点を見ても交点ベクトルの値が一番大きい成分が選ばれていないことにお気づきでしょうか．実は同じことが交点ベクトルツリーとStern-Brocotツリーの場合にも起こっていました．
compare3
交点ベクトル/Stern-Brocotツリーの対応において最大の成分が選ばれないことは以下の定理から容易にわかります：
$\ell\in L_t$を$t\in\TT'$, $F(L,\ell)\neq0$を満たす三角形分割$L_t$の辺とする．このとき，$\mathrm{grad}_L(\ell)=\dfrac{a}{b}$（ただし$\dfrac{a}{b}$は既約分数)であることと$F(L,\ell)=\begin{bmatrix}a-1\\b-1\\a+b-1\end{bmatrix}$であることは同値である．
交点ベクトル/Stern-Brocotツリーの対応は，交点ベクトルの第1成分が分子，第2成分が分母に対応していた（
第3回の定理2
）ので，$t\in\TT'$であるような三角形分割$L_t$の辺の交点ベクトルにおいては（$F(L,\ell)=0$であるようなものを除き）第3成分が常に最大値であることにより，最大の成分が選ばれないことはある意味当然の結果であると言えます．まずは，これの初期交点ベクトル/Calkin-Wilfツリー版を示しましょう．
初期交点ベクトルとCalkin-Wilfツリーの対応は，直前のフリップによって変化した成分以外の2成分に1を足したものをそれぞれ分子分母に配置する対応でした（
第5回の定理1
）ので，次の定理を示せばいいことになります．
$t,t'\in\TT_3'$で$L_{t'}=\varphi_k(L_t)$であるとする．\begin{align*}
F(L_t,\ell_3)=\begin{bmatrix}f_1\\f_2\\f_3\end{bmatrix}\neq 0, \quad F(L_{t'},\ell_3)=\begin{bmatrix}f_1'\\f_2'\\f_3'\end{bmatrix}\neq 0
\end{align*}
としたとき，$f_k$が$F(L_t,\ell_3)$の成分の中で最大値でないことと$f'_k$が$F(L_{t'},\ell_3)$の成分の中で最大値であることは同値．
ちなみに今はそんなに関係ありませんが（ないことはないですが）$i\neq k$のとき$f_i=f'_i$であることは定義からすぐにわかります．
補題3は交点行列の具体的な記述を与えた
第5回の定理8
からでも導出できますが，場合分けが多くて綺麗ではないので別の証明を考えます．そのために，第3回，第5回で使った命題に今回も登場してもらいましょう．
$M=(m_{1},m_{2},m_{3})$を三角形分割，$\{i,j,k\}=\{1,2,3\}$とする．このとき，次の2つの条件は同値である．
次のどちらかの不等式が成立する．
\begin{align} \mathrm{grad}_L(m_{i})<\mathrm{grad}_L(m_{j})<\mathrm{grad}_L(m_{k})\quad \text{or}\quad \mathrm{grad}_L(m_{k})<\mathrm{grad}_L(m_{j})<\mathrm{grad}_L(m_{i}). \end{align}$\dfrac{a}{b}$と$\dfrac{c}{d}$が既約分数で，$\mathrm{grad}_L(m_{i})=\dfrac{a}{b},\mathrm{grad}_L(m_{k})=\dfrac{c}{d}$であるとき，$\mathrm{grad}_L(m_{j})=\dfrac{a+c}{b+d}$である．
特に，任意の三角形分割$M=(m_{1},m_{2},m_{3})$に対して$a,c\in\mathbb Z$と$b,d\in\mathbb Z_{\geq0}$が存在して，$\dfrac{a}{b}$と$\dfrac{c}{d}$が既約分数であって
$$\left\{\mathrm{grad}_L(m_{1}),\mathrm{grad}_L(m_{2}),\mathrm{grad}_L({m_{3}})\right\}=\left\{\dfrac{a}{b},\dfrac{c}{d},\dfrac{a+c}{b+d}\right\}$$
となる．
$M=(m_1,m_2,m_3)$を三角形分割，$\{i,j,k\}=\{1,2,3\}$とする.
\begin{align}
\mathrm{grad}_L(m_i)<\mathrm{grad}_L(m_j)<\mathrm{grad}_L(m_k)
\end{align}
を仮定する．
$M'=\{m_{i},m'_{j},m_{k}\}$を，$M$を$m_j$でフリップした三角形分割とする．このとき，次のどちらかの不等式が成立する．
\begin{align} \mathrm{grad}_L(m'_{j})<\mathrm{grad}_L(m_{i})<\mathrm{grad}_L(m_{k})\quad \text{or}\quad \mathrm{grad}_L(m_{i})<\mathrm{grad}_L(m_{k})<\mathrm{grad}_L(m'_{j}). \end{align}$M''=\{m''_{i},m_{j},m_{k}\}$を，$M$を$m_i$でフリップした三角形分割とする．このとき，このとき，次の不等式が成立する．
\begin{align} \mathrm{grad}_L(m_{j})<\mathrm{grad}_L(m''_{i})<\mathrm{grad}_L(m_{k}). \end{align}$M'''=\{m_{i},m_{j},m'''_{k}\}$ を，$L_t$を$m_k$でフリップした三角形分割とする．このとき，次の不等式が成立する．
\begin{align} \mathrm{grad}_L(m_{i})<\mathrm{grad}_L(m'''_{k})<\mathrm{grad}_L(m_{j}). \end{align}
任意の$t\in\TT'_3$と$i\in\{1,2,3\}$に対して，$\mathrm{grad}_L(\ell_{i;t})\geq0$.
任意の$t\in\TT_3$に対して，次の等式が成立する．
\begin{align*}
F(L_t,L)=(F(L,L_t))^T,
\end{align*}
ただし，$T$は転置を表す．
補題4，命題5，補題6の証明は 第3回の記事 を参照してください．補題7は交点行列の定義を考えれば明らかです．
まず，$f'_{k}$が$F(L_{t'},\ell_3)$において最大値であることを仮定して$f_{k}$が$F(L_{t},\ell_3)$において最大値でないことを示す．$f'_k=0$ならば最大値ではないので， $f'_k\neq0$を仮定する．$f'_k$が$\{f'_1,f'_2,f'_3\}$の中で最大であるとすると，$F(L,L_{t'})$の第$k$列に対応する三角形分割の辺の傾きが真ん中の大きさであることが補題7と定理2，補題4からわかる．命題5から，$F(L,L_{t})$の第$k$列に対応する三角形分割の辺の傾きは真ん中の大きさではない．再び 補題7と定理2，補題4を適用することで，$f_k$は$\{f_1,f_2,f_3\}$の中で最大でないことがわかる．
逆について示す．$f_k$が$F(L_{t},\ell_3)$において最大でないことを仮定する．$f_k\neq 0$であれば，上の議論の逆を辿ることで示される．$f_k=0$のとき，補題6から$F(L,L_t)$の$(3,k)$成分が$f_k=0$であることになる．このとき$F(L,\ell_{k;t})=0$であることが定理2からわかる．よって$\mathrm{grad}_L(\ell_{k;t})$は$0$または$-1$または$\infty$であるが，補題6から$\mathrm{grad}_L(\ell_{k;t})$は$0$または$\infty$である．後の議論は$f_k\neq 0$のときと同様．
以上から，以下の定理が示されました．
第5回の定理1 における初期交点ベクトルツリーとCalkin-Wilfツリーの対応において使用される交点ベクトル$F(L_t,\ell_3)$の2つの成分は，どちらも$F(L_t,\ell_3)$の3つの成分において最大ではない．
さて，もう少しです．ここでさらに少し記号の準備をしましょう．
3次の置換群を$S_3$として，$\sigma\in S_3$と$F(L,\ell))=\begin{bmatrix}f_1\\f_2\\f_3\end{bmatrix}$に対して$\sigma(F(L,\ell))$を
\begin{align*}
\sigma(F(L,\ell))=\begin{bmatrix}f_{\sigma(1)}\\f_{\sigma(2)}\\f_{\sigma(3)}\end{bmatrix}
\end{align*}
と定義しておきます．このとき，以下の事実が成り立ちます．
任意の$t\in\TT_3'$と$i\in\{1,2,3\}$について，ある$\sigma\in S_3$と$s\in\TT'_3,\ j\in\{1,2,3\}$が存在して
\begin{align*}
\sigma(F(L_t,\ell_3))=F(L,\ell_{j;s}).
\end{align*}
この補題は一見非自明に見えますが，実は単純な話です．
第2回の記事
で$L$を取るときに．「どんな1点トーラス上の三角形分割でも，トーラスの普遍被覆を適当に歪めることで下の図の状態とみなすことができる」という話をしました．
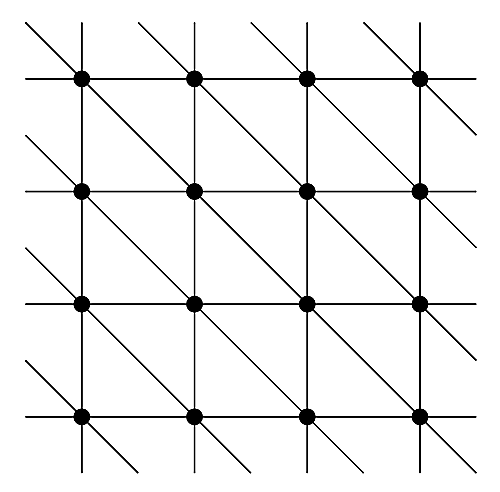torusuniversal
これを補題中の$L_t$に適用してあげるだけです．ただし，$s\in\TT'_3$となるようにするために少し工夫が必要です．
$L$から$L_t$にフリップを繰り返して移る際の最後に移した辺が$k$番目の成分の辺であるとする．このとき適当に被覆写像を取り直すことで，上図の普遍被覆の斜線を$\ell_{k;t}$に対応させ，他の2辺を縦線，横線に対応させるようにする．さらに，$\sigma(3)=k$となる置換$\sigma$をとることで，$s$として$\TT_3'$に属するようなものが取れる．
つまり，三角形分割$L_t$を上図の縦線，横線，斜線と同一視しようとする際に，$\ell_3$を含む三角形分割$L$をフリップを繰り返して得ようとするときはまず最初に斜線に対応する辺をフリップするように調整し，しかもそれが三角形分割における3つ目の成分となるように添字を置換することで$s$を$\TT'_3$の頂点として取ってこれるようにしたわけです．
さて，実はもうほとんどCalkin-Wilfツリーの分数の既約性の証明は終わっています．最後にとどめをさしましょう．
まず最初に，Calkin-Wilfツリーと初期交点ベクトルツリーの対応において使用される交点ベクトル$F(L_t,\ell_3)$は$0$ベクトルではないことに注意しておく．定理8と定理9から，対応に用いられる$F(L_t,\ell_3)$の2つの成分は,ある交点ベクトル$F(L,\ell_{j;s})$（ただし$s\in \TT_3'$）の第1成分と第2成分に一致する．これをそれぞれ$\alpha,\beta$とする．ここで，定理5から$\dfrac{\alpha+1}{\beta+1}$と$\dfrac{\beta+1}{\alpha+1}$は既約分数．Calkin-Wilfツリーにおける$F(L_t,\ell_3)$に対応する分数はこの2つのうちのどちらかであるから，Calkin-Wilfツリーにおける任意の頂点の分数が既約分数であることが示された．
以上でこのシリーズのゴールである定理が証明されました．ここまでお疲れ様でした！
シリーズ完結，でも…？
これにて無事このシリーズは完結…といきたいところですが，まだ少しモヤモヤした感情を持っている人もいるかもしれません．おそらく，
こんなこと考えて何のためになるんだ！？
と思っていらっしゃる方もいるのではないでしょうか（あ，もし証明が間違っている等の理由でモヤモヤしている方がいらっしゃったらコメントをお寄せくださると助かります）．実際，直接証明しようとすればこんな長ったらしい証明を与えなくても良いはずです．確かに，この事実を証明するだけならばここまでやる必要はありません．しかし，この証明の過程で考えたツリー同士の対応は重要な意味を持つと個人的には考えています．もうお気づきかと思われますが，このシリーズで一番僕が伝えたかった事実はツリーの既約性の話ではなくこのStern-Brocotツリー，Calkin-Wilfツリーと交点ベクトルが構成する2つのツリーの対応の話です．次回の記事で，そこら辺の話をして終わりにしようと思います．ということで後もう少しだけ続きます．ここまで読んでくださってありがとうございました．
参考文献
- [Gyo20] Y. Gyoda, Cluster duality between Calkin-Wilf tree and Stern-Brocot tree, 2020. preprint, arXiv:2009.06473 [math.NT]