x^3-3xは美しい
$$ \bm{y=x^3-3x} $$
この記事では，$x^3-3x$に関する問題をいくつか紹介します。有名なものや自作問題です。出典が分かるものについては記載しています。なお，この記事では解答を与えていません。お気持ちだけ述べています。
問題リスト
$x,y$を実数とする。連立方程式
\begin{cases}
y=x^3-3x\\
x^2+y^2=4
\end{cases}
を解きなさい。
定点$\mathrm P$から$3$次関数$y=x^3-3x$に向かって$3$本の接線を引くことが出来るような，点$\mathrm P$の存在する領域を図示しなさい。
次の問いに答えよ。
⑴ 等式$\cos3\theta=4\cos^3\theta-3\cos\theta$を示せ。
⑵ $2\cos80\Deg$は，方程式$x^3-3x+1=0$の解であることを示せ。
⑶ $x^3-3x+1=(x-2\cos80\Deg)(x-2\cos\alpha)(x-2\cos\beta)$となる角度$\alpha,\beta$を求めよ。ただし$0\Deg<\alpha<\beta<180\Deg$とする。
$p$を実数とし，$3$次方程式$x^3-3x-p=0\quad\cdots\cdots(\ast)$を考える。次の問いに答えよ。
⑴ $(\ast)$が異なる$3$つの実数解を持つとき，$p$のとり得る値の範囲を求めよ。
⑵ ⑴のとき，異なる$3$つの実数解を$\alpha,\beta,\gamma$ $(\alpha<\beta<\gamma)$とする。またそのうちの$1$つの解は$x=2\cos\theta$で表されるとする。（$-\bunsuu{\pi}{6}<\theta<\bunsuu{\pi}{6}$）
① $\alpha,\beta,\gamma$を$\theta$を用いて表せ。
② $|3\alpha^2-3|+|3\beta^2-3|+|3\gamma^2-3|$の範囲を求めよ。
定数$p$に対して，$3$次方程式$x^3－3x－p＝0$の実数解の中で最大のものと最小のものとの積を$f(p)$とする。ただし，実数解がただひとつのときには，その$2$乗を$f(p)$とする。
⑴ $p$がすべての実数を動くとき，$f(p)$の最小値を求めよ。
⑵ $y=f(p)$のグラフを書け。
以下，お気持ち表明です。
$\phantom{a}$
$\phantom{a}$
$\phantom{a}$
$\phantom{a}$
$\phantom{a}$
図形との対応
$x,y$を実数とする。連立方程式
\begin{cases}
y=x^3-3x\\
x^2+y^2=4
\end{cases}
を解きなさい。
この問題は次のグラフの交点を求めることに等しいです。（なんなら，この図を見てもらいたいがために記事にしました。）
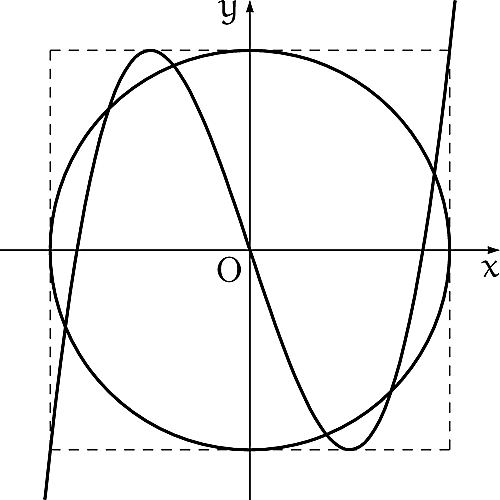3次関数と円
（四角形は，一辺$4$の正方形です。）
ということはつまり，先の連立方程式の解は$6$組あるということが見て取れます。また，その$x$座標や$y$座標を，$\cos$や$\sin$で表してみるのも面白いですね。
ちなみに，昔 こんなプリント を作ったことがあります。
この点は通らねェよォ！！
定点$\mathrm P$から$3$次関数$y=x^3-3x$に向かって$3$本の接線を引くことが出来るような，点$\mathrm P$の存在する領域を図示しなさい。
東進の数学の先生がこの問題を説明している動画があり，その動画自体は非常に有名ですが，問題が取り上げられることは少ないと思います。
いくつかその先生が言っていることを文字起こししてみました。
「だからぁ，この点とこの点とこの点が出るわけだ。この点は出ねぇよぉ！！$(a,b)$を通らねぇ接線なんだから。」
「所詮，手際よく解けるように作られた入試問題という箱庭の中でしかぁ，生きていけない解答に過ぎないんだ。」
この問題を解いた後にその動画を見ると，ネタに出来ないくらい非常に分かりやすいのです。
$3$倍角？
次の問いに答えよ。
⑴ 等式$\cos3\theta=4\cos^3\theta-3\cos\theta$を示せ。
⑵ $2\cos80\Deg$は，方程式$x^3-3x+1=0$の解であることを示せ。
⑶ $x^3-3x+1=(x-2\cos80\Deg)(x-2\cos\alpha)(x-2\cos\beta)$となる角度$\alpha,\beta$を求めよ。ただし$0\Deg<\alpha<\beta<180\Deg$とする。
先ほども，円が絡んできましたが，$x^3-3x$というのは，3倍角との親和性が非常に高いです。理由はこの問題を解けば分かります。初めてこういう問題を解く人は，「こんな$3$次方程式も解けるんだ！」と思わされますね。（ところで，なんで暗黙のうちに，$x^3-3x+1=0$の解の絶対値は$2$未満であると認めているのでしょうかね。。。）
やや一般化
$p$を実数とし，$3$次方程式$x^3-3x-p=0\quad\cdots\cdots(\ast)$を考える。次の問いに答えよ。
⑴ $(\ast)$が異なる$3$つの実数解を持つとき，$p$のとり得る値の範囲を求めよ。
⑵ ⑴のとき，異なる$3$つの実数解を$\alpha,\beta,\gamma$ $(\alpha<\beta<\gamma)$とする。またそのうちの$1$つの解は$x=2\cos\theta$で表されるとする。（$-\bunsuu{\pi}6<\theta<\bunsuu{\pi}{6}$）
① $\alpha,\beta,\gamma$を$\theta$を用いて表せ。
② $|3\alpha^2-3|+|3\beta^2-3|+|3\gamma^2-3|$の範囲を求めよ。
筑波の問題では，$p=1$としていましたが，ここでは$p$を定数として，より広い状況で考えてもらいます。ちなみに⑵の②は， この記事の問題 を考えているときに求めてみたくなったものです。
なんなんだこの問題シリーズ
定数$p$に対して，$3$次方程式$x^3－3x－p＝0$の実数解の中で最大のものと最小のものとの積を$f(p)$とする。ただし，実数解がただひとつのときには，その$2$乗を$f(p)$とする。
⑴ $p$がすべての実数を動くとき，$f(p)$の最小値を求めよ。
⑵ $y=f(p)$のグラフを書け。
やっぱりこの問題は，いつみても不思議です。だって⑵が分かれば⑴も自明なのだから。ということは，⑴をヒントにグラフを書けとでも言っているのでしょうか？（実際そうなのでしょう。）
しかも，⑵ではどこまで増減を調べれば（2階微分はすべきか）良いのかが明示されていないので少し困ります。（ま，1階微分しようと思ってもかなりキツい計算なので，2階微分しようと思わないんですけど。。。）
ちなみに答えのグラフは，見た目的にイラってします。ぜひ考えてみてください。
