石鹸膜の幾何学入門(3): 変分公式からの帰結~極小曲面の凸包~
前回 ははめ込まれた曲面に対して面積の変分を計算し, 面積の臨界点であるための幾何学的条件「平均曲率が至る所$0$」を導きました. そしてこの条件を通して, 改めて極小曲面を定義しました.
今回は, 第一変分公式から導かれる極小曲面のいくつかの性質について見ていきます.
- $x^i$: $\mbb{R}^3$の第$i$座標関数.
- $\{E_i\}_{i=1}^3$: $\mbb{R}^3$の正規直交基底.
- $\nabla$: $\mbb{R}^3$上の微分(Levi-Civita接続).
- $\{e_j\}_{j=1}^{2}$: $\Sigma$上のフレーム(正規直交標構)
- $\nablaS$: $\Sigma$上のLevi-Civita接続.
- $\mrm{div}^\Sigma=\sum_i \inn{\nabla_{e_i}\cdot}{e_i}$: $\Sigma$に沿ったベクトル場の発散.
- $\lapS=\mrm{div}^\Sigma\circ \nablaS$: $\Sigma$上のラプラシアン.
$\Sigma$に沿った任意のコンパクト台を持つ変分ベクトル場$V$に対し
\begin{align}
\left.\frac{d}{dt}\right|_{t=0}\area{\Sigma_t}=-\int_{\Sigma}2H\inn{V}{N}=\int_{\Sigma}\divS{V}.
\end{align}
極小曲面と座標関数
$\Sigma$を$\mbb{R}^3$内の曲面とします. $\mbb{R}^3$の第$i$座標成分$x^i$を$\mbb{R}^3$上の実数値関数と思い, それを$\Sigma$上に制限したものを考えます(同じ記号$x^i$で表すことにします).
曲面$\Sigma$が極小曲面であるための必要十分条件は, 任意の$i$に対して関数$x^i$が調和関数($\lapS x^i=0$)になることである.
はじめに, $E_i=\nabla x^i$であることに注意する. 任意の$\phi \in C_0^{\infty}(\Sigma)$を取り, $\Sigma$に沿ったベクトル場$\phi E_i$を考える. 任意の$X\in\mathfrak{X(\Sigma)}$に対し$\nabla_{X} E_i=0$となるので,
\begin{align}
\divS{\phi E_i}=\sum_j\inn{\nabla_{e_j}(\phi E_i)}{e_j}
=\sum_j\inn{(e_j \phi)E_i}{e_j}=\sum_j\inn{E_i}{(e_j \phi)e_j}=\inn{\nablaS \phi}{E_i}
\end{align}
第一変分公式より
\begin{align}
-\int_{\Sigma}\phi\inn{E_i}{2HN}=\int_{\Sigma}\divS{{\phi E_i}}=\int_{\Sigma}\inn{\nablaS \phi}{E_i}=\int_{\Sigma}\inn{\nablaS \phi}{\nablaS x^i}.
\end{align}
最後の等式では$\nabla x^i$の接成分が$\nablaS x^i$に等しいことを用いた.
発散定理により
\begin{align}
\int_{\Sigma}\inn{\nablaS \phi}{\nablaS x^i}=\int_{\Sigma}\divS{\phi\nablaS x^i}-\int_{\Sigma}\phi \lapS x^i=-\int_{\Sigma}\phi \lapS x^i
\end{align}
となるので,
\begin{align}
\int_{\Sigma}\phi\inn{E_i}{2HN}=\int_{\Sigma}\phi \lapS x^i
\end{align}
が任意の$\phi$に対して成り立つ.
変分法の基本補題より
\begin{align}
\lapS x=(\lapS x^1, \lapS x^2, \lapS x^3)=2HN
\end{align}
となるから, $H=0$となる必要十分条件は$\lapS x=0$.
この命題から直ちに次がわかります.
$\mbb{R}^3$内の境界を持たないコンパクト極小曲面は存在しない.
そのような極小曲面$\Sigma$が存在したとする.
命題1より
\begin{align}
\lapS (x^i)^2=2x^i\lapS x^i+|\nablaS x^i|^2=|\nablaS x^i|^2.
\end{align}
これを積分すると, 発散定理より$\int_{\Sigma} |\nablaS x^i|^2=0$となり, したがって各$x^i$は定数関数でなければならない. これは$\Sigma$が一点のみからなることを意味し, 曲面であることと矛盾する.
よって, 極小曲面として興味のある対象は, コンパクトで空でない境界を持つ場合か非コンパクトな場合に限定されます.
Convex hull property
ここでは, 曲面$\Sigma$はコンパクトかつ空でない境界を持つと仮定します.
弱最大値原理と極小曲面の凸包
座標関数の調和性から導かれる, ある幾何学的帰結について述べます.
部分集合$A\subset\mbb{R}^n$に対し, $A$を含む全ての閉半空間の共通部分を$A$の凸包(the convex hull of $A$)と言い, $\mrm{Conv}(A)$と表す.
$\Sigma$をコンパクトな極小曲面とすると, $\Sigma \subset \mrm{Conv}(\partial \Sigma)$.
感覚的には, 枠$\partial\Sigma$を張る石鹸膜$\Sigma$の外側から石鹸膜に向かって徐々に手のひら(平面)を近づけていったとき, 手のひらが最初に触れるのは必ず枠$\partial\Sigma$上の点である, という性質です. この性質からも, 取りうる石鹸膜の形状はかなり限定的になるということが読み取れます.
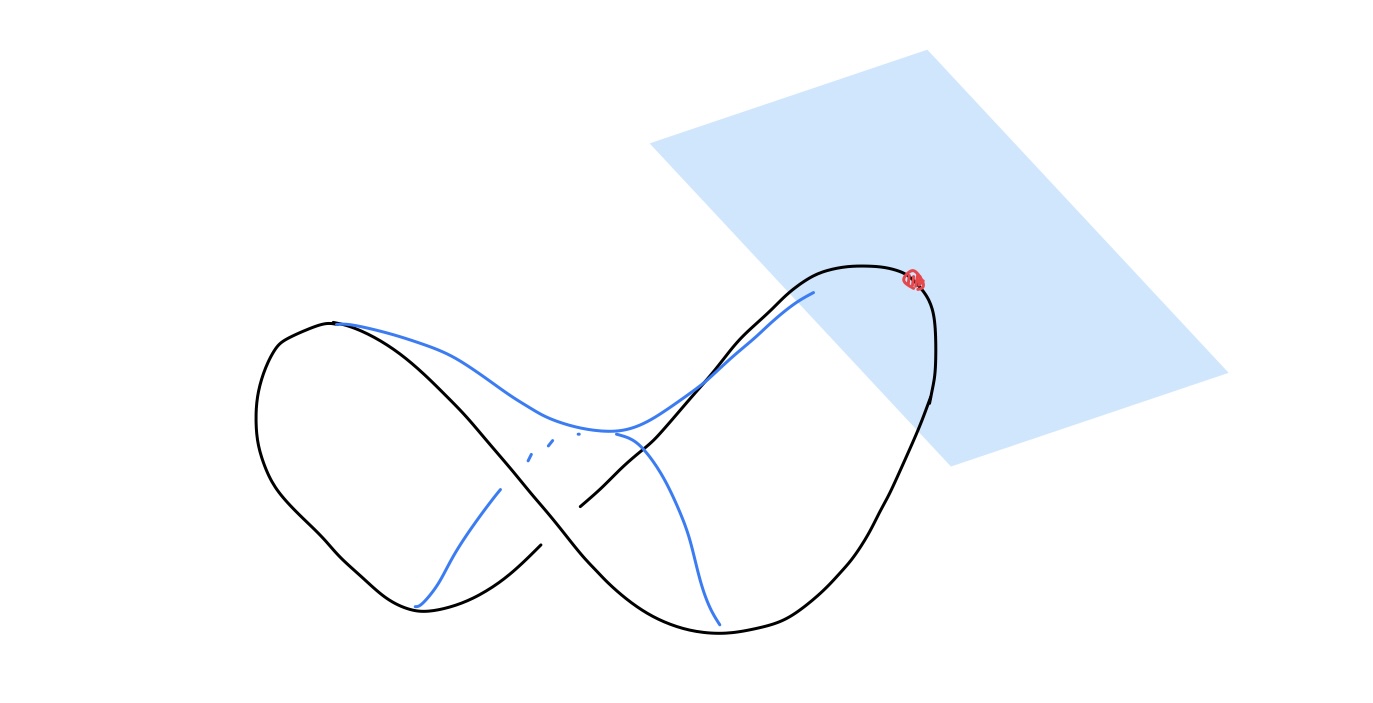平面が最初に触れるのは境界上の点
証明の前に, 調和関数の持つ次の性質を思い出しておきます.
$\Sigma$をコンパクトRiemann多様体とし, $u$をその上の調和関数とする. このとき
\begin{align}
\max_{\Sigma}u=\max_{\partial\Sigma}u
\end{align}
が成り立つ. さらに, もし$u$が$\Sigma$のある内点で最大値を持てば, $u$は定数である.
今は曲面で考えているため, 等温座標系を用いれば通常のラプラシアンの最大値原理に帰着されます. 一般の場合の証明は少し大変です. 長くなるため, 詳細は折り畳みをご覧ください.
最大値原理の証明
関数$u$の最大値を$m_0=\max_{\Sigma}u$とおき, 集合$\Omega=u^{-1}(m_0)$を考える. 定め方から, $\Omega$は$\Sigma$の閉集合. $\Sigma$のある内点が$\Omega$に含まれていたならば, $\Omega$が開集合でなければならないことを示す. これが示されれば, 連結性から$\Omega=\Sigma$でなければならず, したがって$u$は定数関数となる.
そこで, $\Omega$が内点を持っていたとし, 任意の$p_0\in\Sigma\setminus\partial\Sigma \cap \Omega$を取る. 正の数$R>0$を$2R<\min{\{\mrm{inj}(p_0), \mrm{dist}(p_0, \partial \Sigma)\}}$を満たすように取り, 測地球$B_{2R}^{\Sigma}(p_0)$を考える. このとき$B_{R}^{\Sigma}(p_0)\subset\Omega$となることを示そう.
いま, $p \in B_{R}^{\Sigma}(p_0)\setminus \Omega$を満たす点があったとし, $\rho=\mrm{dist}(p, p_0)$とおく. このとき, $B_{\rho}^{\Sigma}(p)\subset B_{2R}^{\Sigma}(p_0)$に注意する. したがって, 点$p$からの距離関数$r(x)=\mrm{dist}(x, p)$は, $B_{\rho}^{\Sigma}(p)\setminus \{p\}$でなめらかである. また, $0<\delta<\rho$を小さく取り, $B_{\delta}^{\Sigma}(p)$上で$u< m_0$が成り立つようにしておく.
ここで, $a \in \mbb{R}$を後で決める定数とし, $B_{\rho}^{\Sigma}(p)$上の関数$v$を
\begin{align}
v=e^{-ar^2}-e^{-a\rho^2}
\end{align}
で定義する. $A(\delta, \rho)=B_{\rho}^{\Sigma}(p)\setminus B_{\delta}^{\Sigma}(p)$上で$\lapS v$を計算すると, $|\nablaS r|=1$に注意して,
\begin{align}
\lapS v &=\divS{-2are^{-ar^2}\nablaS r}\\
&=-2are^{-ar^2}-2ae^{-ar^2}|\nablaS r|^2+4a^2r^2e^{-ar^2}|\nablaS r|^2\\
&=e^{-ar^2}(4a^2r^2-2a(1+r\lapS r))\\
&\geq e^{-ar^2}(4a^2\delta^2-2a(1+\sup_{A(\delta, \rho)}|r\lapS r|))
\end{align}
となる. よって, $a>0$を十分大きく取れば, $A(\delta, \rho)$上で$\lapS v>0$とできる.
そこで, 任意の$\eps>0$に対して$u_{\eps}=u+\eps v$とおくと, $A(\delta, \rho)$上で$\lapS u_\eps>0$となる.
もし, $u_\eps$が$A(\delta, \rho)$の内部で最大値を取ったとすると, この点において$\mrm{Hess}_{u_\eps}\leq 0$となり, したがって$\lapS u_\eps =\tr({\mrm{Hess}_{u_\eps}}) \leq 0$とならねばならない. よって, $u_\eps$は$A(\delta, \rho)$の境界で最大値を取る.
$\eps>0$を小さく取れば, $u_\eps$の最大値は$p_0\in\partial B_{\rho}^\Sigma(p)$で達せられることを示そう. そのためには, $u_\eps(p_0)\geq\sup_{B_{\delta}^{\Sigma}(p)}u_\eps$を示せばよい. 定め方から$v(p_0)=0$であることに注意して条件を変形すると,
\begin{align}
u(p_0)\geq \sup_{B_{\delta}^{\Sigma}(p)}(u+\eps(e^{-ar^2}-e^{-a\rho^2}))
\end{align}
となる. ここで, $\delta$の取り方から$u(p_0)>\sup_{B_{\delta}^{\Sigma}(p)}u$であることに注意して,
\begin{align}
\eps = \frac{u(p_0)-\sup_{B_{\delta}^{\Sigma}(p)}u}{2(e^{-a\delta}-e^{-a\rho^2})}
\end{align}
とおくと, $B_{\delta}^{\Sigma}(p)$上で
\begin{align}
u+\eps(e^{-ar^2}-e^{-a\rho^2})&=u+\frac{e^{-ar^2}-e^{-a\rho^2}}{2(e^{-a\delta^2}-e^{-a\rho^2})}(u(p_0)-\sup_{B_{\delta}^{\Sigma}(p)}u)\\
&\leq u+\frac{u(p_0)-\sup_{B_{\delta}^{\Sigma}(p)}u}{2}\\
&= \frac{u+u(p_0)}{2}+\frac{u-\sup_{B_{\delta}^{\Sigma}(p)}u}{2}\\
&\leq u(p_0)
\end{align}
が成り立つ. したがって$u_\eps$は$p_0$で最大値を取ることがわかった.
このとき, $u_\eps$の$p_0 \in \partial B_{\rho}^{\Sigma}(p)$における外向き法方向微分は
\begin{align}
\frac{\partial u_\eps}{\partial r}(x_0)\geq 0
\end{align}
を満たす. $u_\eps=u+\eps v$より,
\begin{align}
\frac{\partial u}{\partial r}(x_0)\geq -\eps\frac{\partial v}{\partial r}(x_0)=2\eps a\rho e^{-a\rho^2}>0.
\end{align}
ところが, $u$は内点$p_0$で最大値を取るから, このことは$\nablaS u(p_0)=0$であることと矛盾する.
以上により, $B_R^{\Sigma}(p_0)\subset \Omega$がわかり, したがって$u$が定数関数でなければならないことがわかった.
境界$\partial\Sigma$を含む任意の半空間$H$を取る. このとき$\Sigma\subset H$を示せばよい.
ある単位ベクトル$v\in\mbb{S}^2$と実数$a\in\mbb{R}$を用いて
\begin{align}
H=\{x\in\mbb{R}^3 | \inn{x}{v}\leq a\}
\end{align}
と表せることに注意する.
命題1と同様にして, $\Sigma$上の関数$u(x)=\inn{x}{v}$は調和関数であることがわかるから, 最大値原理により$u$は境界$\partial\Sigma$で最大値を取る. このことから, 任意の$x\in\Sigma$に対して,
\begin{align}
\inn{x}{v}=u(x)\leq \max_{\partial\Sigma}u \leq a
\end{align}
となり, $\Sigma\subset H$がわかった.
トポロジー単調性
Convex hull propertyの応用として, 極小曲面が次の意味で位相的に単調であることが示せます.
$\Sigma$をコンパクトかつ単連結な極小曲面とする. $K\subset\mbb{R}^3$を$K\cap \partial\Sigma=\emptyset$を満たす任意のコンパクト凸集合とするとき, $K\cap\Sigma$も単連結である.
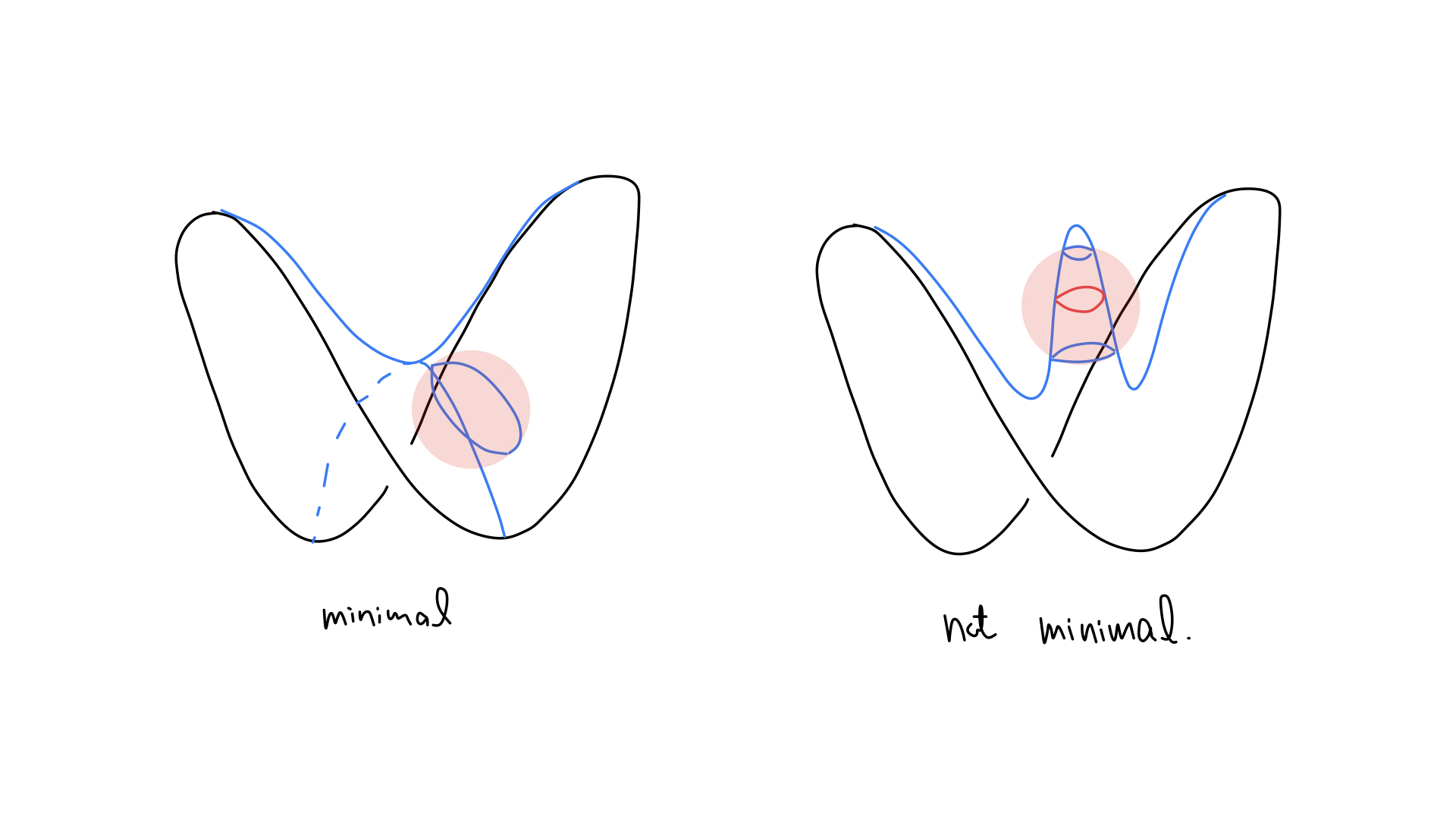単調性を満たす例と満たさない例
背理法により示す. $K\cap\Sigma$が単連結でないとすると, $K\cap\Sigma$の中で可縮でない閉曲線$\gamma \subset K\cap\Sigma$が存在する. 一方, $\Sigma$自体は単連結だから, $\gamma$は$\Sigma$の中では可縮である. よって, 単連結部分領域$D\subset\Sigma$で, $\partial D=\gamma$であるようなものが存在する. 作り方から, $D\not\subset K$である.
一方, この$D$もコンパクトな極小曲面だから, convex hull propertyにより$D\subset\mrm{Conv}(\gamma)\subset K$でなければならず, 矛盾する.
もう少しトポロジー的な言葉で表現するなら, 包含$\iota: K\cap\Sigma \to \Sigma$が誘導する基本群の準同型$\iota_{*}: \pi_1(K\cap\Sigma)\to\pi_1(\Sigma)$が単射になることを主張しています.
おわりに
今回は第一変分公式から導かれる帰結の中でも, とりわけ幾何学的なものを紹介しました. 今回の記事を通して, 極小曲面のかたちはかなり制限されてそうだという雰囲気が伝わったでしょうか. 変分公式のもう一つの帰結として単調性公式と呼ばれるそれ自体重要な公式もあるのですが, こちらはまた機会を改めて紹介しようと思います.
次回は再びグラフ極小曲面について考えます.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
