絡み数とホップ束
はじめに
はじめまして、三日月湖です。 駒場理数豚汁カレンダー 10日目 の記事です。みなさん、 豚汁 の美味しさの秘密ってなんだと思いますか?
正解は「いろんな具材の美味しさが複雑に絡み合っていること」です。
というわけで、美味しい豚汁を求めて、「絡まる」ということについてちょっと考えてみましょう。
(Mathlog初投稿にもかかわらず突貫工事となったことにより、非常に見苦しい記事となってしまいました。ご容赦ください。)
(ふんわりと読んでいただけると幸いです。)
捻れと絡み
帯の捻れ
「絡まる」と聞いて思い浮かぶのって、だいたい紐みたいな1次元のものですよね。2次元的なものは「捻れてる」ことが多い気がします。例えば、細長い長方形の紙の両端を、$(180×n)°$捻って貼り合わせた輪$M_n$を考えてみます($n \in \mathbb{Z} $)。$M_1$(メビウスの帯)や$M_2$は、捻れてない自明な帯$M_0$とどう違うのでしょうか?
![!FORMULA[6][35635404][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FSDaBr6hkihIxXrCqyRHP.jpeg?alt=media) $M_n$
$M_n$
$M_0$と$M_1$の大きな違いは、裏表の有無(向き付け可能性)です。$M_0$は明らかに裏表があります(向き付け可能である)が、$M_1$は片方の面を辿っていくと、いつのまにか最初の裏側に来てしまいます(向き付け可能でない)。別の言い方をすると、始点をくっつけた2本の(区別された)矢印を描き、そのまま帯上で適当に動かしたとき、いつのまにか2本の矢印が逆向きになってしまうようなことがあれば向き付け不可能、なければ向き付け可能です。
![!FORMULA[11][35635404][0]の向き付け可能性](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F80rwFiO8X5EV17dDy0yv.jpeg?alt=media) $M_n$の向き付け可能性
$M_n$の向き付け可能性
また、境界(ふち)を見ることでも区別できます。$M_0$の境界は2本の円ですが、$M_1$の境界は1本に繋がっています。
紐の絡み
一方、$M_0$と$M_2$はどう区別されるのでしょうか?$M_2$には裏表があるので、$M_1$のようにはいきません。実は、$M_0$と$M_2$は、繋がり方が同じなので図形として同じ(位相空間として同相)なんです。でも明らかに$M_2$は捻れてますよね。$M_2$が持っている捻れは、図形が3次元空間にどのように置かれているか($\mathbb{R} ^3$にどう埋め込まれているか)を考えることで初めて検出できる「外在的な捻れ」です。境界を見てみると、$M_0$の境界も$M_2$の境界も、どちらも2本の紐からなりますが、$M_0$の方はバラバラなのに対し、$M_2$の方は絡まっているように見えます。このように、複数の紐が3次元空間において絡み合っているものを、絡み目と呼びます。ここでは紐が2本の場合だけ考えます。
$S^1$で2次元平面$\mathbb{R}^2$内の単位円を表します。$S^1$には反時計回りで向きが入っているものとします。同様に、n次元球面$S^n$を$\mathbb{R}^{n+1}$において原点からの距離が1の点全体とします。
$S^1$の$S^3$への埋め込みの像を結び目という。
$S^1$の向きから自然に結び目の向きが定まります。$S^3$は$\mathbb{R}^3$に無限遠点$\infty$を付け加えたものだと思えるので、とりあえずほぼ$\mathbb{R}^3$だと思っても大丈夫です。
交わらない2つの結び目$K_1,K_2$の合併$K_1 \cup K_2$を(2成分の)絡み目という。
同様に、多成分の絡み目も定義されます。
2つの結び目や絡み目があるときに、一方を、途中で自己交差が生じないように$S^3$内でなめらかに変形して、もう一方に(向きを込めて)重ねられるとき、2つはアイソトピックであると言います。アイソトピックなものは、ほぼ同じものとみなせます。
絡み目の絡み具合を表す数を次のように定義してみます。
交わらない2つの結び目$K_1,K_2$の絡み数(まつわり数)$Lk(K_1,K_2)$を、次のように定める;
$K_1,K_2$を(交点が三重以上にならないように)$\mathbb{R}^2$に射影した図における$K_1$と$K_2$の交点を、以下のように符号付きで数えて、$ \frac{1}{2} $倍したもの。
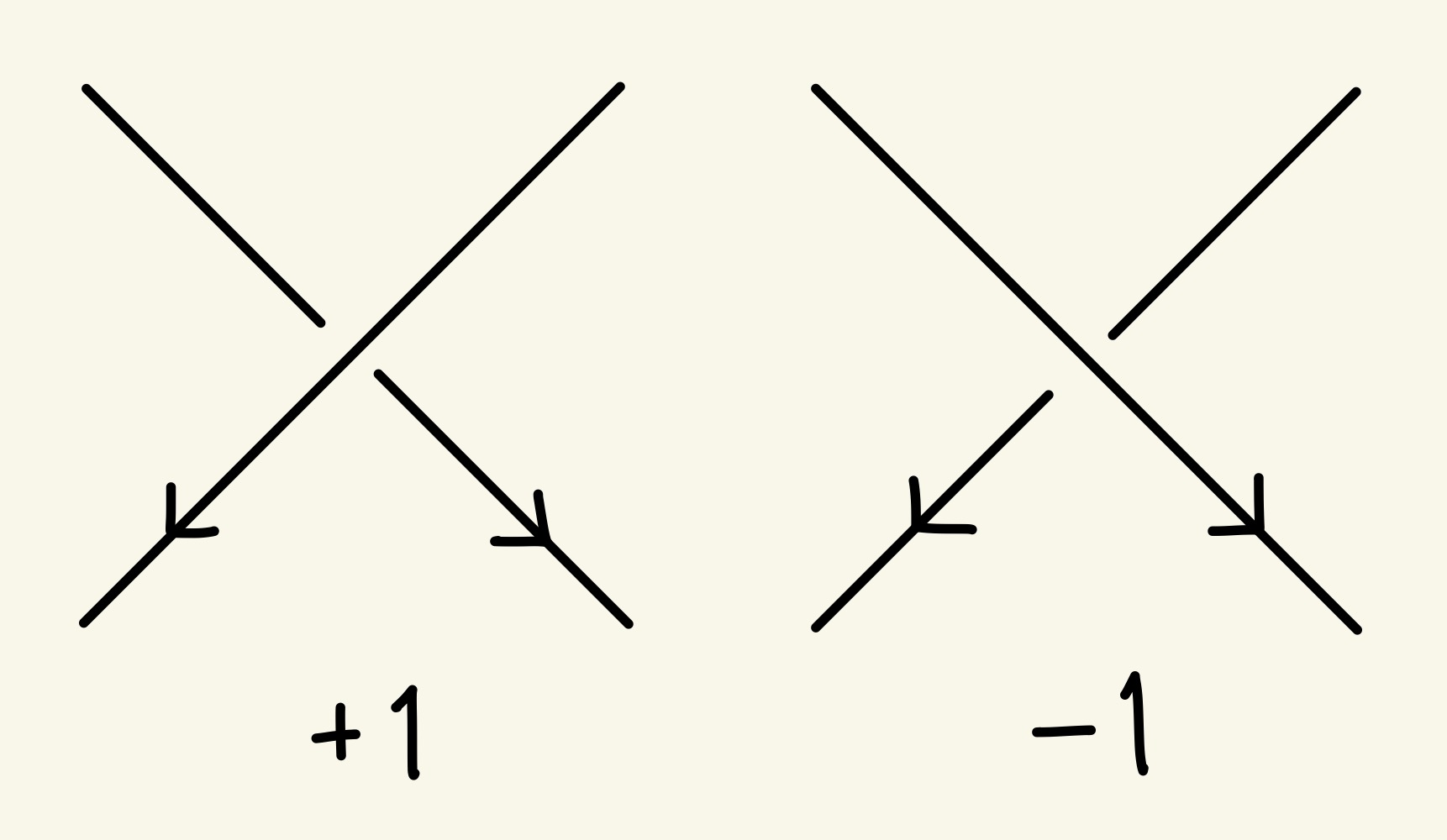 射影図における交点の符号
射影図における交点の符号
この絡み数の定義はどう射影するかにめちゃくちゃ依存しているのでwell-defined性を確かめなければいけませんが、より一般的に、(射影の仕方を固定しておいて)アイソトピックなら絡み数が等しいことを確かめておきます。実はアイソトピックな2つの絡み目の射影図は、ライデマイスター移動と呼ばれる次のような3種類の局所的な変形によって、一方からもう一方に移せることが知られています。
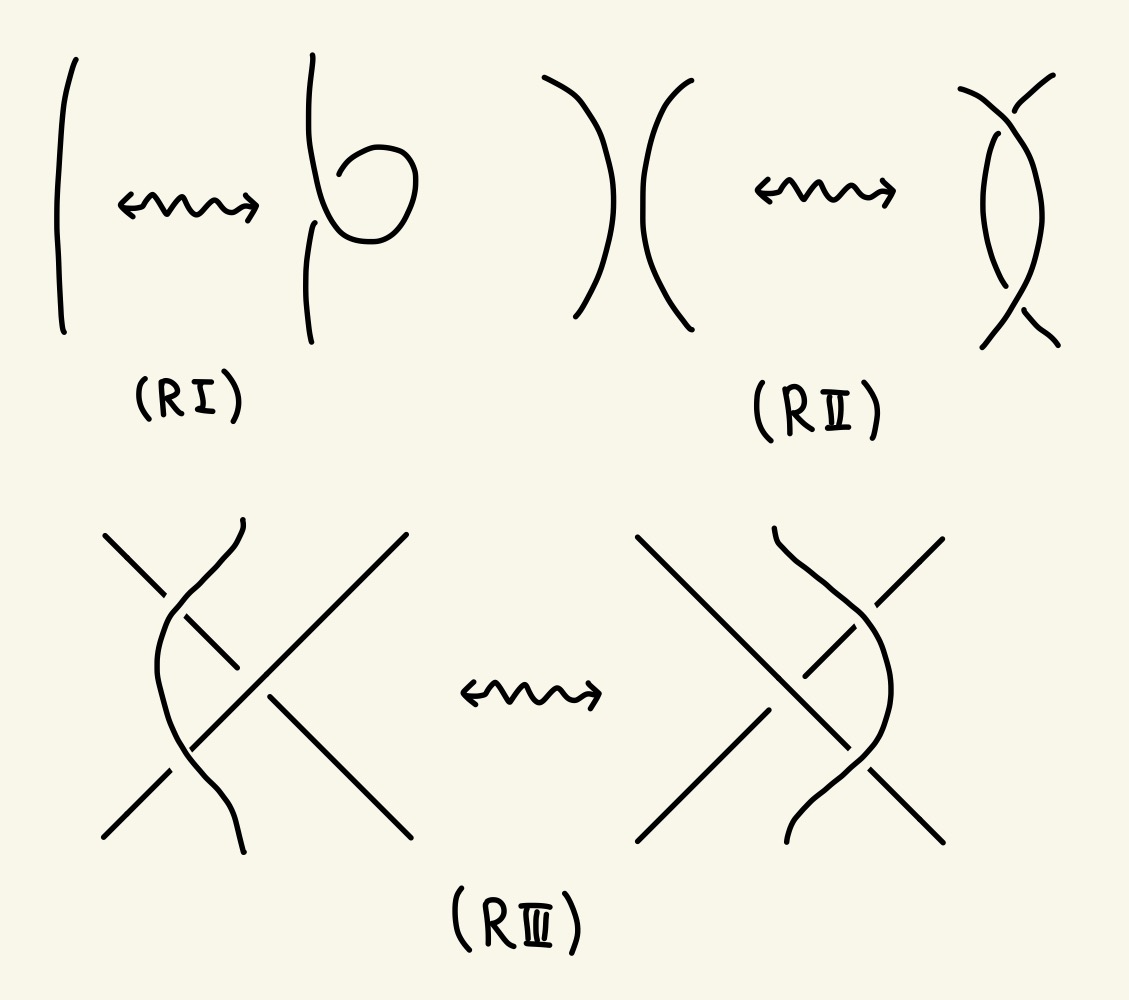 ライデマイスター移動
ライデマイスター移動
RⅠはそもそもひとつの結び目内での変形なので絡み数に影響はなく、RⅡでは交点の符号が打ち消し合い、RⅢでは交点の符号が保たれます。よって絡み数はアイソトピックで不変となります。
さて、絡み数で本当に$M_0$と$M_2$が区別されるのか確認しましょう。帯の表を適当に決めて、表からみて反時計回りになるように、帯の境界にも向きを入れておきます。
![!FORMULA[51][35633482][0]と!FORMULA[52][35633544][0]の境界の絡み数](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FHMu7xFK0Vmr5CBwSXW6F.jpeg?alt=media) $M_0$と$M_2$の境界の絡み数
$M_0$と$M_2$の境界の絡み数
図より、$M_0$の境界の絡み数は$\frac{1-1}{2}=0$、$M_2$の境界の絡み数は$\frac{1-3}{2}=-1$となります。同様にして、$M_{2n}$の境界の絡み数は$-n$であることがわかります。(最初に$M_{n}$の捻る向きを適当に決めたのでマイナスが付いちゃいました。逆向きに捻っておけば$M_{2n}$の境界の絡み数は$n$になります。)
絡み数のいろいろな定義
ここでは絡み数を射影図の符号付き交点数で定めましたが、この定義はとても数えやすい一方、ちょっと高次元に一般化しにくいです。他にもいろいろな定義の仕方があり、例えば
- 一方の結び目を境界に持つ曲面(ザイフェルト曲面)と、もう一方の結び目との符号付き交点数
- $K_1×K_2 \rightarrow S^2;(x,y) \mapsto \frac{x-y}{|x-y|} $の写像度
- ガウスの積分による表示$$\frac{1}{4 \pi} \int_{K_1} \int_{K_2} \frac{(x-y)\cdot (dx×dy)}{|x-y|^3} $$
などがあります。
ホップ束
ファイバー束
自明な帯$M_0$とメビウスの帯$M_1$は、帯という言葉が表す通り、どちらも円周$S^1$に線分$[-1,1]$が並んだものと考えることができます。このように、「ある図形Bの上に別の図形Fが並んで、全体の図形Eが構成されている」という構造をファイバー束といいます。このとき、「EにはB上のF束の構造が入る」といい、$F↪︎E→B$と書いたりします。
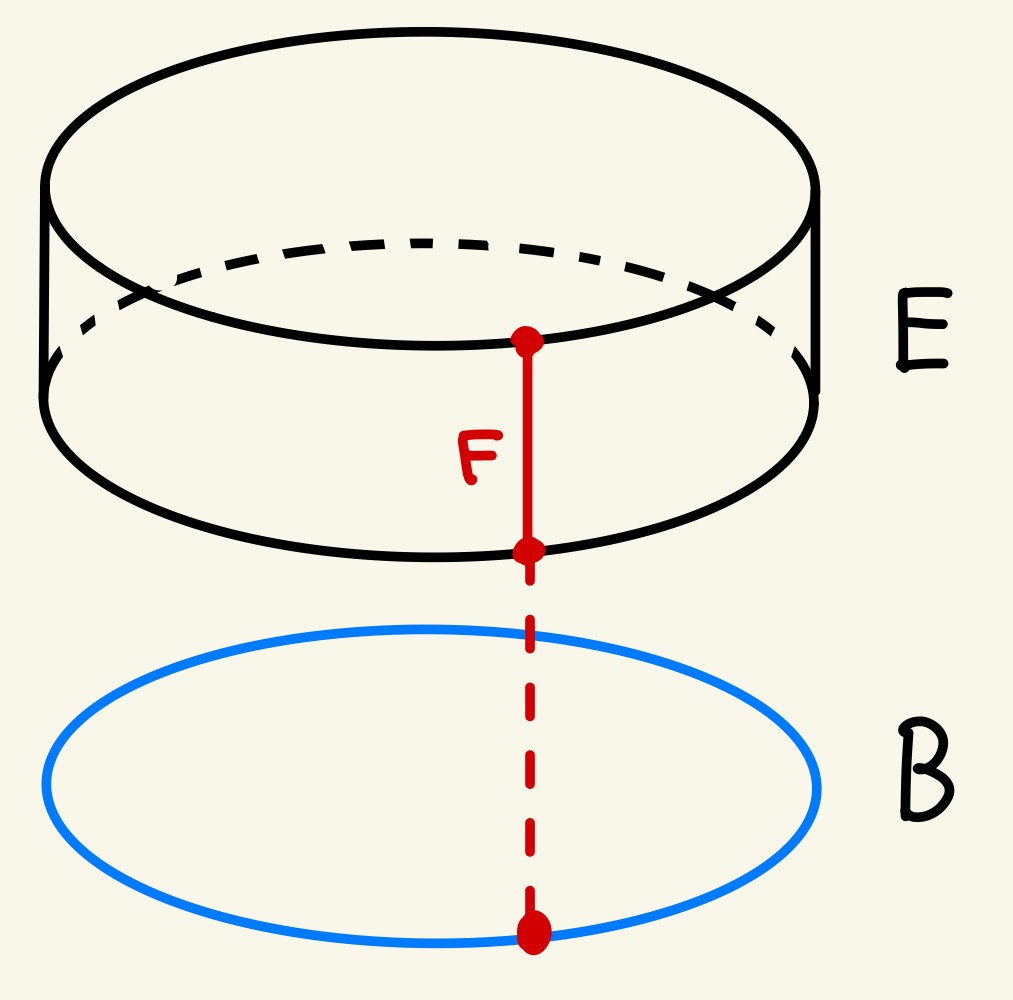 ファイバー束のイメージ
ファイバー束のイメージ
$M_0$と$M_1$にはどちらも$S^1$上の$[-1,1]$束の構造が入りますが、$M_0$は$[-1,1]$が「まっすぐ」並んでいるのに対し、$M_1$は捻れています。$M_0$のようにファイバーが捻れずに並んでいるものを自明束といいます。$M_1$は自明束ではありませんが、適当に帯を切ってしまえば捻れはまっすぐにできるので、「局所的には自明である」と思えます。ファイバー束にはこの「局所自明性」を課します(ファイバーがあまりに乱雑に並んでいても困るので)。
例えば、自明な帯$M_0$の2本の境界を素直に貼り合わせたものはトーラス$T^2=S^1 \times S^1 $であり、これは$S^1$上の(自明な)$S^1$束になります。では2本の境界を逆向きに貼り合わせるとどうなるでしょうか?(これは$ \mathbb{R}^3 $内では自己交差してしまいますが、もっと高い次元内で考えたり、あるいはそもそも外側の空間なんてないものとすれば問題なく考えられます。)これも$S^1$上の(捻れた)$S^1$束であり、クラインの壺と呼ばれます。
![!FORMULA[85][35811298][0]上の!FORMULA[86][35811298][0]束](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FFVckrZbw1VZM5a8THjSj.jpeg?alt=media) $S^1$上の$S^1$束
$S^1$上の$S^1$束
ホップ束
もう少し複雑なファイバー束を考えてみましょう。$\mathbb{C}^2$の単位球面$S^3$から、複素射影直線$ \mathbb{C}P^1$への写像$f$を
$$
f:S^3 \rightarrow \mathbb{C}P^1 ;\\\\
(z,w) \mapsto [z:w]
$$
で定めます。$[α:β] \in \mathbb{C}P^1$の逆像を考えてみます。$f(z,w)=[α:β] $とすると、ある$λ \in \mathbb{C} \setminus \{0\} $が存在して、$ (z,w)=(λα,λβ) $となります。 いま、$(z,w) \in S^3$より$|z|^2+|w|^2=1$なので、$|λ|= \frac{1}{\sqrt {|α|^2+|β|^2}}$となります。この値を$R>0$とすると、ある$\theta \in [0,2 \pi)$を用いて$λ=R e^{i \theta}$と書けます。よって、$$
f^{-1}([\alpha:\beta]) = \left\{ e^{i \theta} \left( \frac{\alpha}{\sqrt{|\alpha|^2+|\beta|^2}} , \frac{\beta}{\sqrt{|\alpha|^2+|\beta|^2}} \right) : \theta \in [0,2 \pi) \right\}
$$
となります。これは$S^1$と同相です。ところで$\mathbb{C}P^1$は$S^2$と同一視されるので、(局所自明性をきちんと確かめると)$f$が$S^3$の$S^2$上の$S^1$束としての構造を与えることが分かります。これをホップ束といいます。
$S^3$を立体射影により$ \mathbb{R} ^3 \cup \{\infty \}$とみなすと、$S^2$の各点の逆像(ファイバー)は、$ \mathbb{R} ^3 $の座標を$(s,t,u)$として
- 北極のファイバー:直線と無限遠点$\lbrace s=t=0 \rbrace \cup \lbrace \infty \rbrace$
- 南極のファイバー:円周$\lbrace s^2+t^2=1, u=0\rbrace$
- 他の点のファイバー:あるトーラス面上の円周
となります。ここで、$S^2$の緯線の逆像はトーラスになり、$ \mathbb{R} ^3 $は、直線(北極のファイバー)、円周(南極のファイバー)と、この直線を中心軸、円周を芯とする層状の無数のトーラスに分割されることになります。("Hopf fibration"で画像検索すれば綺麗な図が無限に出てきます。)
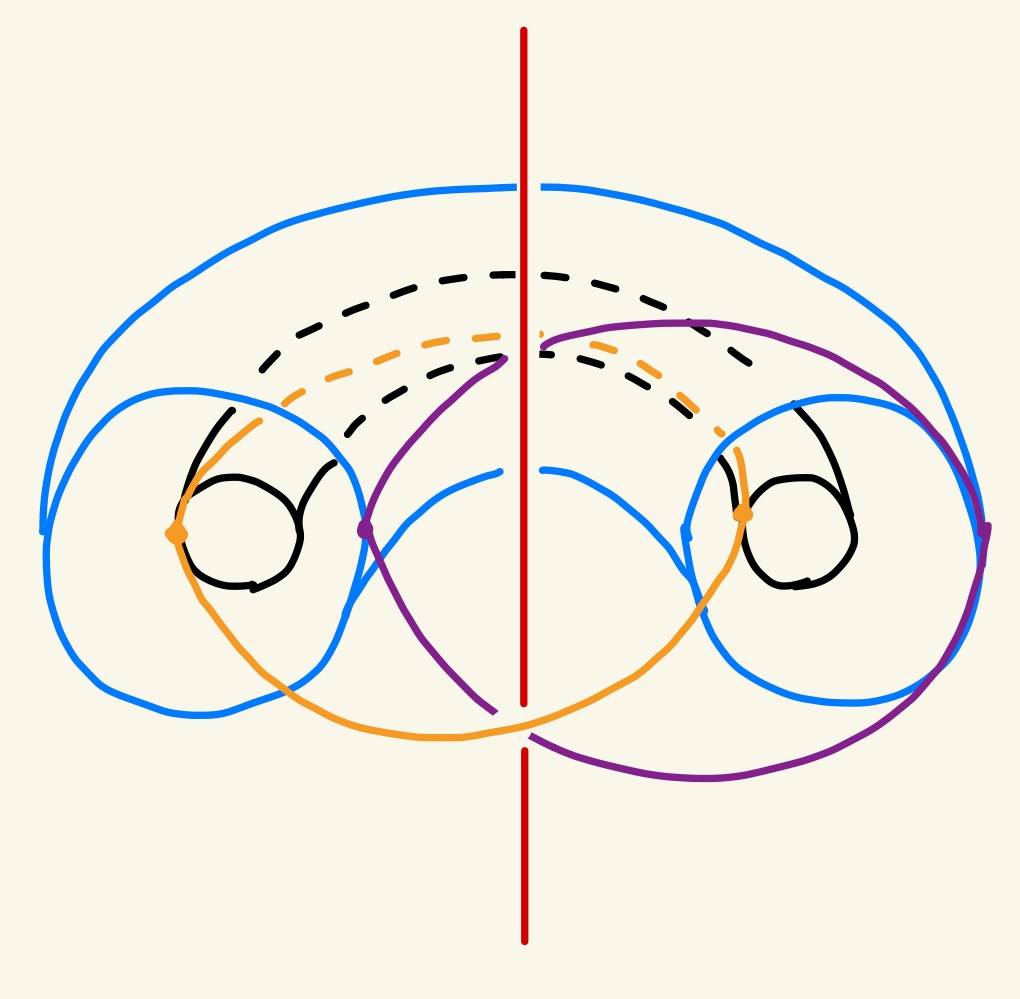 ホップ束のファイバー
ホップ束のファイバー
$f$による$S^2$の各点のファイバーは$S^3$内の(自明な)結び目になっており、それらは交わらないので、適当な2点$b_1,b_2 \in S^2$に対し、(ファイバーに良い感じに向きを定めることで)それらのファイバーの絡み数$$Lk(f^{-1}(b_1),f^{-1}(b_2))$$が定まります。どんな2点を取ってもこの絡み数は常に1になります(図から感じ取ってください)。
ホップ不変量
さきほどの議論は、実はどんな滑らかな写像$f:S^3 \rightarrow S^2 $に対しても行うことができます。$f$が全射でないときはH(f)=0とします。$f$が全射のとき、$S^2$の点(で$f$の正則値であるもの)の逆像は(多成分の)絡み目になり、2点$b_1,b_2 \in S^2$に対し、成分ごとの絡み数の和$Lk(f^{-1}(b_1),f^{-1}(b_2))$は2点の選び方に依りません(!)。これを$f$のホップ不変量といい、$H(f)$と書きます。さらに、$H(f)$が整数値しか取らないことから、$H(f)$は$f$を滑らかに動かしても変わりません(つまり、ホップ不変量はホモトピー不変量)。
連続写像を滑らかな写像で近似することにより、ホップ不変量は$S^2$の3次ホモトピー群$π_3(S^2)$から$\mathbb{Z}$への写像を与えますが、ホモトピー群の加法の定義からこれは群準同型になることが分かります。さらに、ホップ束のホップ不変量が1であることから、$π_3(S^2) \cong \mathbb{Z}$となります。
さらに
本記事で扱ったホップ束$ S^1↪︎S^3→S^2 \cong \mathbb{C}P^1
$と同様にして、実数$\mathbb{R}$や四元数$ \mathbb{H} $、八元数$ \mathbb{O} $を用いて$$
S^0↪︎S^1→S^1 \cong \mathbb{R}P^1$$ $$
S^1↪︎S^3→S^2 \cong \mathbb{C}P^1$$ $$
S^3↪︎S^7→S^4 \cong \mathbb{H}P^1$$ $$
S^7↪︎S^{15}→S^8 \cong \mathbb{O}P^1
$$
というファイバー束が定まります。絡み数も高次元に一般化することで、$f:S^{2n-1}→S^n \\ (n>1)$に対しホップ不変量$H(f)$が定まり、上のファイバー束のホップ不変量は1になります。したがって$n=2,4,8$に対しては$H(f)=1$となる$f:S^{2n-1}→S^n$が存在することになります。なんと、このような$f$が存在するのはこの$n=2,4,8$に限ることが示されています(Hopf invariant one problem)。
おわりに
素朴に導入した絡み数という量が、捻れという構造の複雑さを巧みに表現しており、さらに高次元の絡みを記述するホモトピー群というトポロジーの重要な対象へとつながっていく面白さを伝えたかったです。時間があるときにまた向き合いたいと思います。読んでいただきありがとうございました。
駒場祭に来て豚汁を食べましょう。
