ライツアウトの代数的解法

線形代数,ゲーム,ライツアウト

はじめに

mathlogのグラフ理論のタグを見ていたらライツアウトの記事があった。[2]
昔ライツアウトについては調べたことがあるのでここで共有する。

解くプログラムを作った。スマホの方が見やすいと思う。
https://ipotazero.github.io/lights-out-generator/

形式化

ONの状態を1、OFFの状態を0とする。
スイッチをいくつか押して全てOFFにできるか調べる。

光り方の条件

参考記事では十字に光るライツアウトについて考えていたが、これは一般化できる。

条件

スイッチ$S$を押すと、$S$は光る。(反射律)
$S_0$を押したとき$S_1$が光るなら、$S_1$を押したとき$S_0$は光る。(対称律)

このような光り方を満たすライツアウトについて考える。

方程式

$m$個のスイッチ$S_0,S_1,...,S_{m-1}$があるとする。

盤面の各スイッチのON/OFFを$\mathbb{F}_2$上の列ベクトル$b$として表す。

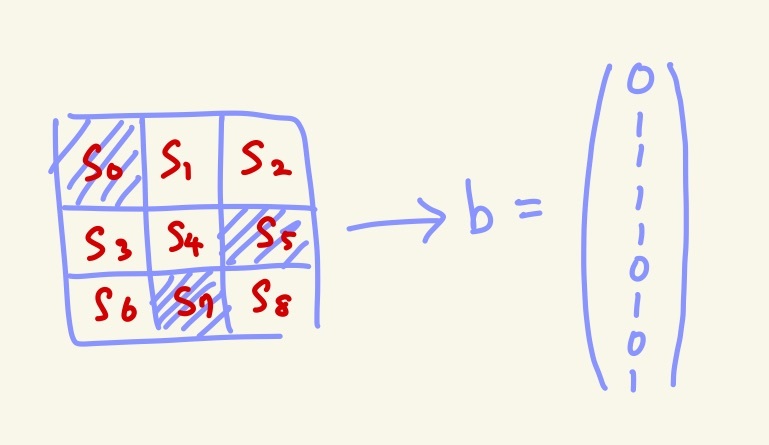斜線の入ったスイッチはOFF=0

スイッチを押す操作は、盤面ベクトル$b$に$\mathbb{F}_2$上のベクトルを足すこととして表せる。
この操作は結合的かつ可換である。

各スイッチを押した時に足されるベクトルを$v_0,v_1,...,v_{m-1}\in \mathbb{F}_2^m$とする。

$G=(v_0,\ v_1,\ ...,\ v_{m-1})$という$m\times m$行列を考える。

$x = (x_0,x_1,...,x_{m-1}) \in \mathbb{F}_2^m$を操作を表すベクトルとする。($x_i$=1のとき$S_i$を押す)

$Gx=x_0v_0+x_1v_1+...+x_{m-1}v_{m-1}$は、全てのスイッチがOFFの状態から$x$で表される操作を行ったとき盤面がどうなっているかを表している。

ある盤面から全てのスイッチをOFFにするには、$Gx+b=0$となる$x$を見つければよい。

今は$\mathbb{F}_2$上で考えているから、$Gx=b$を解けばよい。

この議論は盤面の形や、スイッチを押したときにどのように周りが光るかに依らずに成り立つ。

可解性

どんな盤面状態$b$でも解けるということは$G$が全射ということ。
$G$は正方行列だからこのとき$G$は正則になる。
(よって、どんな盤面状態でも解けるならば答えは一つしかない。)

逆に解けない盤面状態が存在するならば、$\ker(G)$の分の自由度が生まれる。

全反転可能か？

あるスイッチ$S_0$を押して別のスイッチ$S_1$が光った時、逆に$S_1$を押すと$S_0$が光る。
よって$G$は対称行列になる。

スイッチ$S$を押したとき$S$も光るため、$G$の対角成分は全て1である。

$\mathbb{F}_2$上の対称行列は対角成分を並べたベクトルを像に持つ。 1

この命題より、どんなグラフ上の盤面でも、全てOFFの状態から全てONの状態にできる。
参照先は英語の論文なので、日本語訳を書いておく。

$\mathbb{F}_2$上の対称行列$G$を取り、その対角成分を$d$とおく。
$\ker(G)^⊥=\im(^tG)=\im(G)$だから$\forall x \in \ker(G),\ x \cdot d=0$を示せばよい。

$x \in \ker(G)$を取る。
$x=0$の時は明らか。

$x\not=0$の時

一般性を失うことなく$x=(1,1,...,1,0,0,...,0)$(最初の$k+1$個が$1$)と仮定できる。
なぜなら、この形になるように$G$の行と列を同時に入れ替えればよいから。

$G=(a_0,a_1,...,a_{m-1})$とおくと、$Gx=a_{0}+a_{1}+...+a_{k}=0$だから
$\forall j \in \{0,...,m-1\}, a_{j0}+a_{j1}+...+a_{jk}=0$
よって、$\forall j \in \{0,...,m-1\}, a_{jk}=\sum_{l=0}^{k-1}a_{jl}=a_{jj}+\sum_{l=0,l\not=j}^{k-1}a_{jl}$

$j=k$のとき、
\begin{align} a_{kk}&=\sum_{l=0}^{k-1}a_{kl}\\ &=\sum_{l=0}^{k-1}a_{lk}\\ &=\sum_{l=0}^{k-1}(a_{ll}+\sum_{i=0,i\not=l}^{k-1}a_{li})\\ &=\sum_{l=0}^{k-1}a_{ll}+\sum_{l=0}^{k-1}\sum_{i=0,i\not=l}^{k-1}a_{li}\\ &=\sum_{l=0}^{k-1}a_{ll}+2\sum_{k-1 \geq i \gt l \geq 1}a_{il}\\ &=\sum_{l=0}^{k-1}a_{ll}\\ \end{align}

よって、
$x \cdot d = \sum_{l=0}^{m-1}x_ld_l = \sum_{l=0}^{k}a_{ll} = a_{kk} + \sum_{l=0}^{k-1}a_{ll} = 0$