レムニスケート周率のΓ関数表示
はじめに
みなさん,レムニスケート曲線はご存知ですか?
$$(x^2+y^2)^2=a^2(x^2-y^2)$$
という式.または,
$$r^2=a^2\cos{(2\theta)}$$
という極方程式で表せます.
楕円,双曲線の仲間で,
『2つの焦点からの距離の積が一定』
というものです.
いつも通り,Desmosの提供です笑!
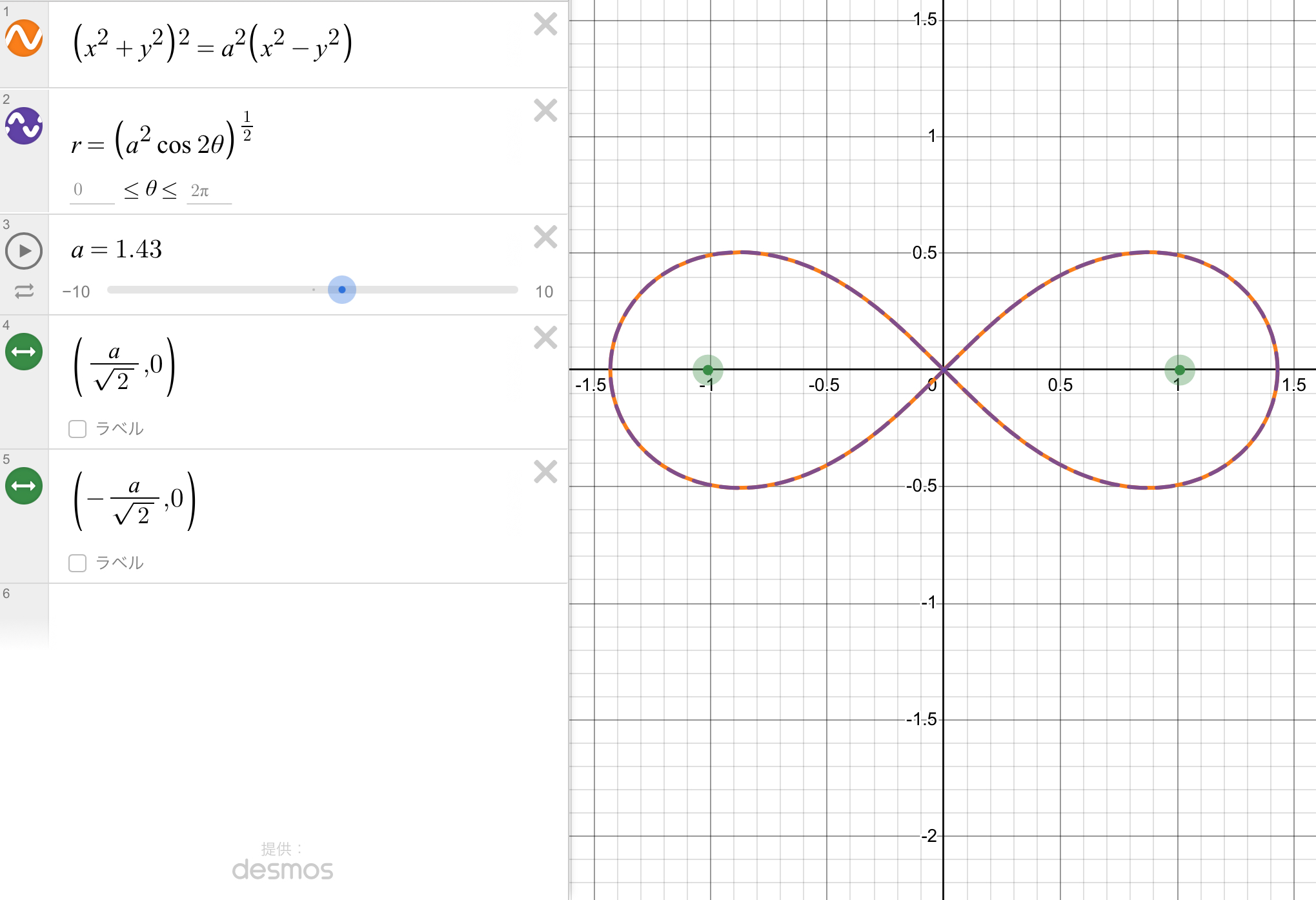
2つの焦点とは緑の点のことです.
今回はこれに関する,レムニスケート周率というものをガンマ関数で表したいという記事です.
レムニスケート周率ってのは曲線の周長と$2a$の比のことです.
レムニスケート周率$\varpi$を$\Gamma$関数を用いて表せ.
前回の記事はほぼ,このためのものでした.
めっちゃ余談ですけど
$\varpi$って\varpiって書くんですね笑
($\pi$は\piです.)
本題
レムニスケート周率$\varpi$を$\Gamma$関数を用いて表せ.
まずレムニスケート曲線の弧長積分を考える.
周長を$L$とする.
$$r^2=a^2\cos{(2\theta)}$$
$$2r\dfrac{dr}{d\theta}=-2a^2\sin{(2\theta)}$$
$$\dfrac{dr}{d\theta}=\dfrac{-a^2\sin{(2\theta)}}{r}$$
対称性から$0\to\frac{\pi}{4}$を4倍すれば良い.
$$L=4\int_{0}^{\frac{\pi}{4}}\sqrt{r^2+\biggl(\dfrac{dr}{d\theta}\biggl)^2}d\theta=4\int_{0}^{\frac{\pi}{4}}\sqrt{r^2+\biggl(\dfrac{a^2\sin{(2\theta)}}{r} \biggl)^2}d\theta$$
$r^2=a^2\cos{(2\theta)}$より,
$$L=4\int_{0}^{\frac{\pi}{4}}\sqrt{r^2+\biggl(\dfrac{a^2\sin{(2\theta)}}{r} \biggl)^2}d\theta=4\int_{0}^{\frac{\pi}{4}}\sqrt{\dfrac{r^4+a^4\sin^2{(2\theta)}}{r^2}}d\theta=4\int_{0}^{\frac{\pi}{4}}\sqrt{\dfrac{a^4\cos^2{(2\theta)}+a^4\sin^2{(2\theta)}}{a^2\cos{(2\theta)}}}d\theta=4a\int_{0}^{\frac{\pi}{4}}\dfrac{1}{\sqrt{\cos{2\theta}}}d\theta$$
$ $
最後の式を$\sin{\theta}=\dfrac{x}{\sqrt{1-x^2}}$で置換すると,
$$L=4a\int_{0}^{1}\dfrac{dx}{\sqrt{1-x^4}}$$
となり,
$$\dfrac{L}{2a}=\varpi=2\int_{0}^{1}\dfrac{dx}{\sqrt{1-x^4}}$$
$x^4=t$と置換すると,
$$\varpi=2\int_{0}^{1}\dfrac{\dfrac{1}{4}t^{-\frac{3}{4}}}{\sqrt{1-t}}dt=\dfrac{1}{2}\int_{0}^{1}t^{-\frac{3}{4}}(1-t)^{{-\frac{1}{2}}}dt$$
ベータ関数$B(x,y)$を用いて,
$$\varpi=\dfrac{1}{2}\biggl(\dfrac{1}{4},\dfrac{1}{2}\biggl)=\dfrac{1}{2}\dfrac{\Gamma\biggl(\dfrac{1}{4}\biggl)\Gamma\biggl(\dfrac{1}{2}\biggl)}{\Gamma\biggl(\dfrac{3}{4}\biggl)} $$
$\Gamma\biggl(\dfrac{1}{2}\biggl)=\sqrt{\pi}$より,
$$\varpi=\dfrac{\sqrt{\pi}}{2}\dfrac{\Gamma\biggl(\dfrac{1}{4}\biggl)}{\Gamma\biggl(\dfrac{3}{4}\biggl)}$$
$ \Gamma(x)\Gamma(1-x)=\dfrac{\pi}{\sin{\pi x}}$より,$x=\dfrac{1}{4}$のとき,
$$\Gamma\biggl(\dfrac{1}{4}\biggl)\Gamma\biggl(\dfrac{3}{4}\biggl)=\dfrac{\pi}{\sin{\dfrac{\pi}{4}}}=\pi\sqrt{2}$$
$$\Gamma\biggl(\dfrac{3}{4}\biggl)=\dfrac{\pi\sqrt{2}}{\Gamma\biggl(\dfrac{1}{4}\biggl)}$$
これを先ほどの式に代入すると,
$$\varpi=\dfrac{\Gamma\bigl(\frac{1}{4}\bigl)^2}{2\sqrt{2\pi}}$$
がわかる.
レムニスケート周率のガンマ関数表示は次のようにできることが示された.
$$\varpi=\dfrac{\Gamma\bigl(\frac{1}{4}\bigl)^2}{2\sqrt{2\pi}}$$
だいぶ綺麗ですよね.
おまけで$\varpi$に収束する無限級数を置いていきます.
完全楕円積分の級数展開とレムニスケート周率が楕円積分の特殊値であることから,
$$\varpi=\dfrac{\pi}{\sqrt{2}}\sum_{n=0}^{\infty}\dfrac{(2n)!^2}{(n!)^4\cdot 32^n}$$
が成り立ちます.綺麗だ!!!
最後まで読んでいただきありがとうございました😊
