嘘か真か？位数２の元からなる可換群の位数は２の累乗！？ 《設定編》
初めに
実は、今回登場する問題は、私も答えが分かっていない問題です。
【設定編】・【問題編】の二つの記事にまたがる長い問題ですが、エピローグまで読んでくだされば幸いです。
ニュートンのアトリエ ～リンカーシャンの錬金術師～
ニュートンのアトリエ（ロゴ）
とある世界のとある国、リンカーシャン。
この国の 真ん中 に『 世界の 取りまとめ 』とあだ名された大きな城下町がありました。一方、この国の いっちばんはしっこ に『世界の 落ちこぼれ』とあだ名された小さな女の子が住んでおりました・・・。
あなたは誰？
あなたは、テーブルゲームを作るある小さな会社に派遣社員としてやってきました。。『ニュートンのアトリエ ～リンカーシャンの錬金術師～』（以下、『アトリエ』）は、会社が一丸となって作成に取り組んでいる超大作。
しかしこの『アトリエ』、ゲームシステムに小さいけれども重要な問題があったようで・・・。
「よし、まずはどんなシステムか見てみよう。」
『アトリエ』は様々なゲームパートからなるゲームです。その中でも一番のメインとなるパートが、【合成パート】です。
【合成パート】では、いくつかの素材カードから新たなカードを生成することが目的になります。
このパートの概要
『アトリエ』では初めに、参加者から一名のゲームマスター（ゲームの進行役。以下『GM』）を選びます。それ以外の参加者はプレイヤー（このゲームの勝敗で遊ぶ役。 ２～６人を推奨。）となります。
一度受け持った役割は、ゲームが終わるまで変更することはできません。
そして【合成パート】では、各プレイヤーが何枚かのカードを手札として持っている状態から始まります。（プレイヤーが扱うカード達を『素材カード』と呼びます。）
各プレイヤーがこのパートを行う順番はあらかじめ決まっており、一人ずつ順番に次の手順をこなしていきます。
GM（１人）とプレイヤー（２～６人）。
手順１、手札から「２枚」または「３枚」のカードを場に出す
【合成パート】が始まり自分のターンがくると、プレイヤーは手札から素材カードを2枚または3枚選びます。選んだカードは手札から引き、ステージにある〈素材カード置き場〉(以下『場』)に並べます。
素材カード置き場。
手順２、GMが【合成テーブル】に基いて一枚のカードを決定する
プレイヤーが〈素材カード置き場〉にカードを並べたら、次にGMが動きます。GMはゲームスタート時に用意した【合成テーブル】をもとに、場に出された素材カードの組み合わせから、別の素材カードを一枚決定します。（この手順1、手順２の行為をまとめて、場に出された素材カードを合成する、または新しい素材カードを生成するといいます。）
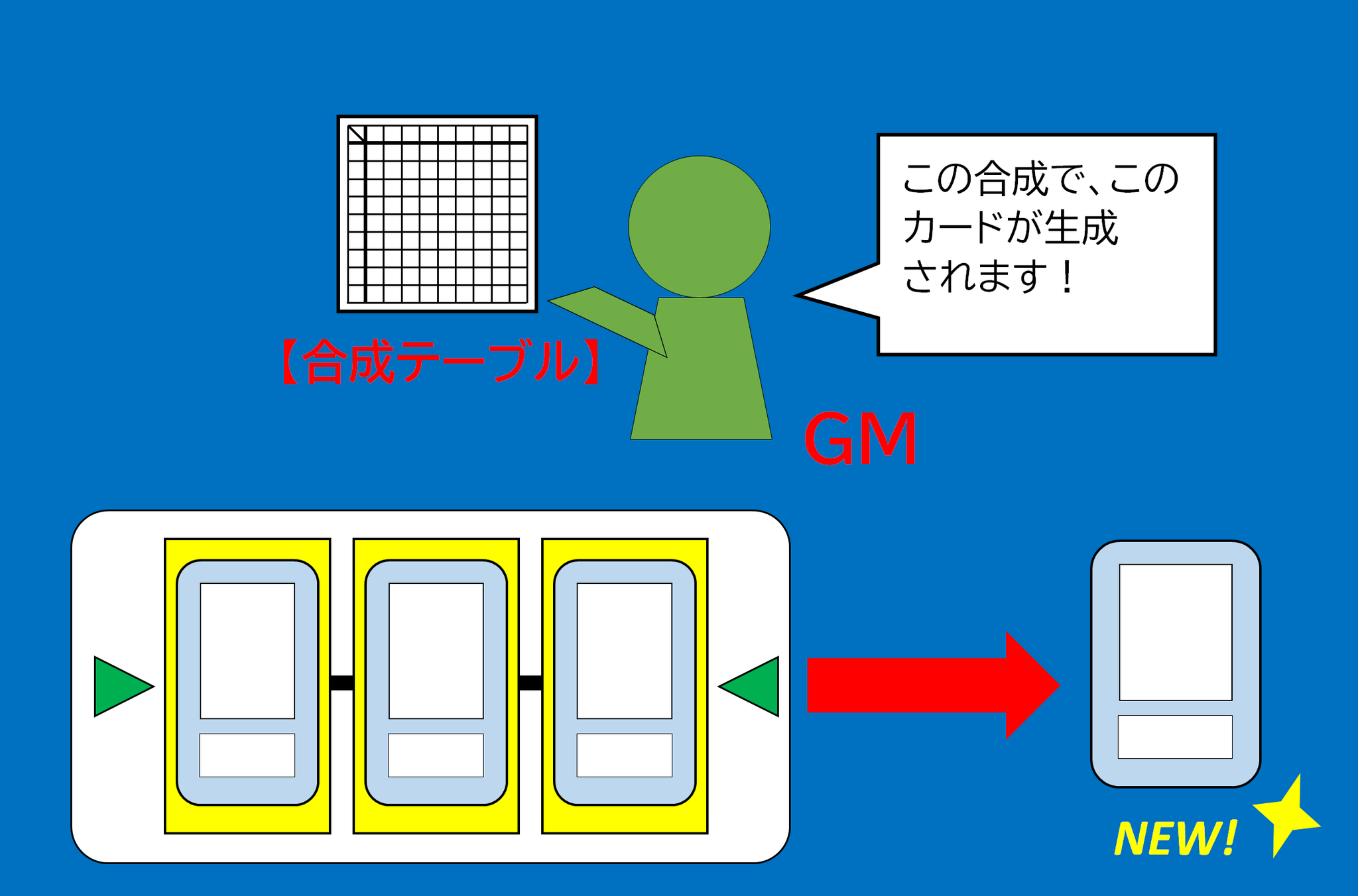【合成テーブル】に基づいて、場に出された素材カード達を合成して、新しいカードを生成する。
手順３、決定した素材カードをプレイヤーに渡す
GMは、生成された素材カード（つまり、手順２でGMが決定した素材カード）を〈山札〉から一枚取り、素材カードを合成したプレイヤー（つまり、手順１で場に素材カードを出したプレイヤー。）に渡します。素材カードを渡されたプレイヤーは、そのカードを自分の手札に入れます。
（手札に入れた素材カードは、また次の機会に使用することができます。）
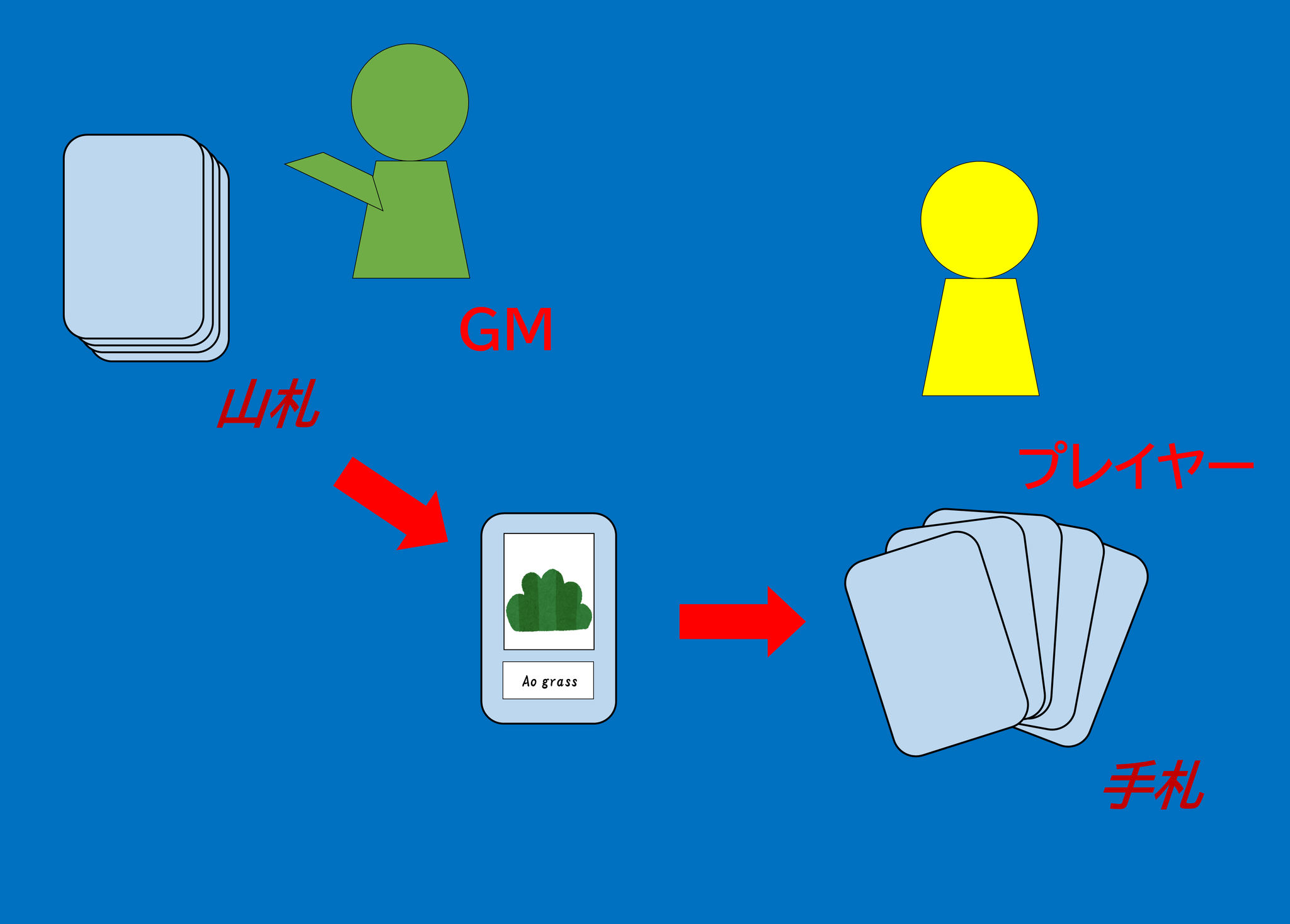山札から素材カードを取り出し、プレイヤーに渡す。
手順４、次のプレイヤーに交代する
一人のプレイヤーが手順１～３まで行った後、あらかじめ決めた順番で次に当たるプレイヤーがまた手順１～３を行います。
この流れを、すべてのプレイヤーが行うまで繰り返します。
手順５、次のパートに入る
全てのプレイヤーが行動したら、この【合成パート】は終了し、次のパートへ移ります。
「この 【合成テーブル】 っていうのは何だ？」
【合成テーブル】・・・これは、場に出された素材カード達から、ある一つのカードを生成する際の規則を作る表になります。『アトリエ』セット内に5枚入っており、ゲームを始めるごとに1枚だけ使用します。
どのように規則をつくるか
合成テーブル（プレーン）。
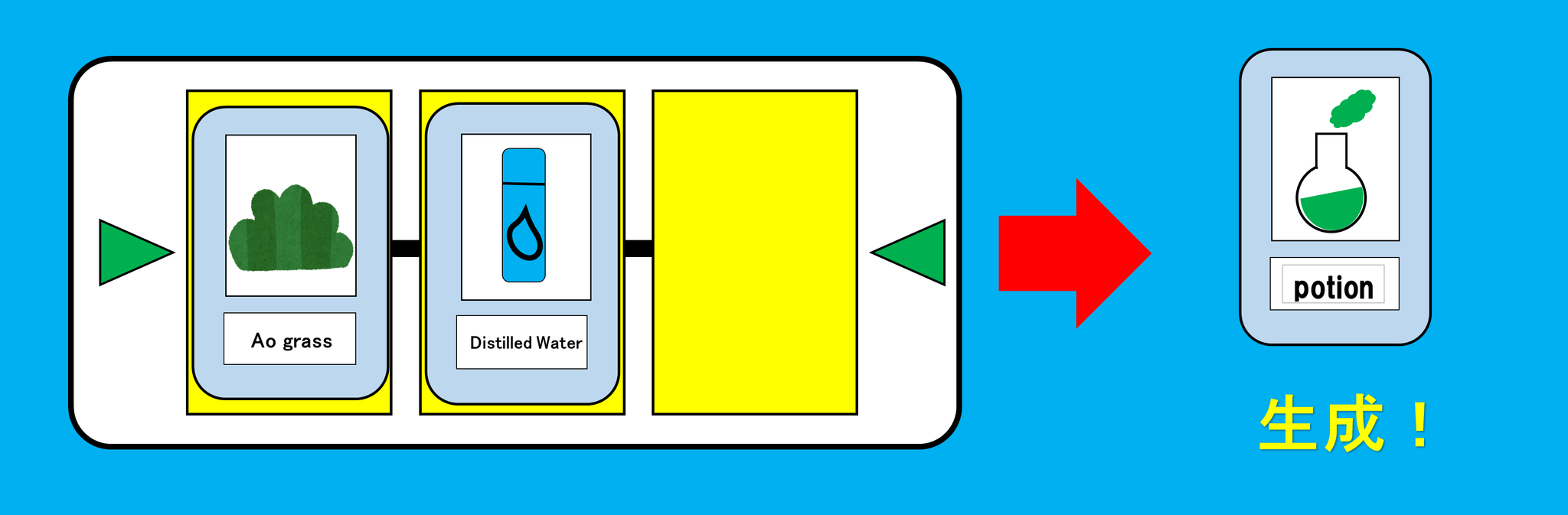
【合成テーブル】は上のような表です。 一番上の横一列 と、一番左の縦一列 から場に出された素材カードと同じものを一つずつ選び、それぞれ選んだものから下方向と右方向に進んで重なったところにあるものが、生成された素材カードとなります。
例えば、素材カードとして『青草』、『蒸留水』が場に置かれたとき、一番上から『青草』、一番左から『蒸留水』を探します。そして『青草』のある列と『蒸留水』のある列の重なる部分を探すと『ポーション』があり、これが今回の合成によって生成された素材カードになります。
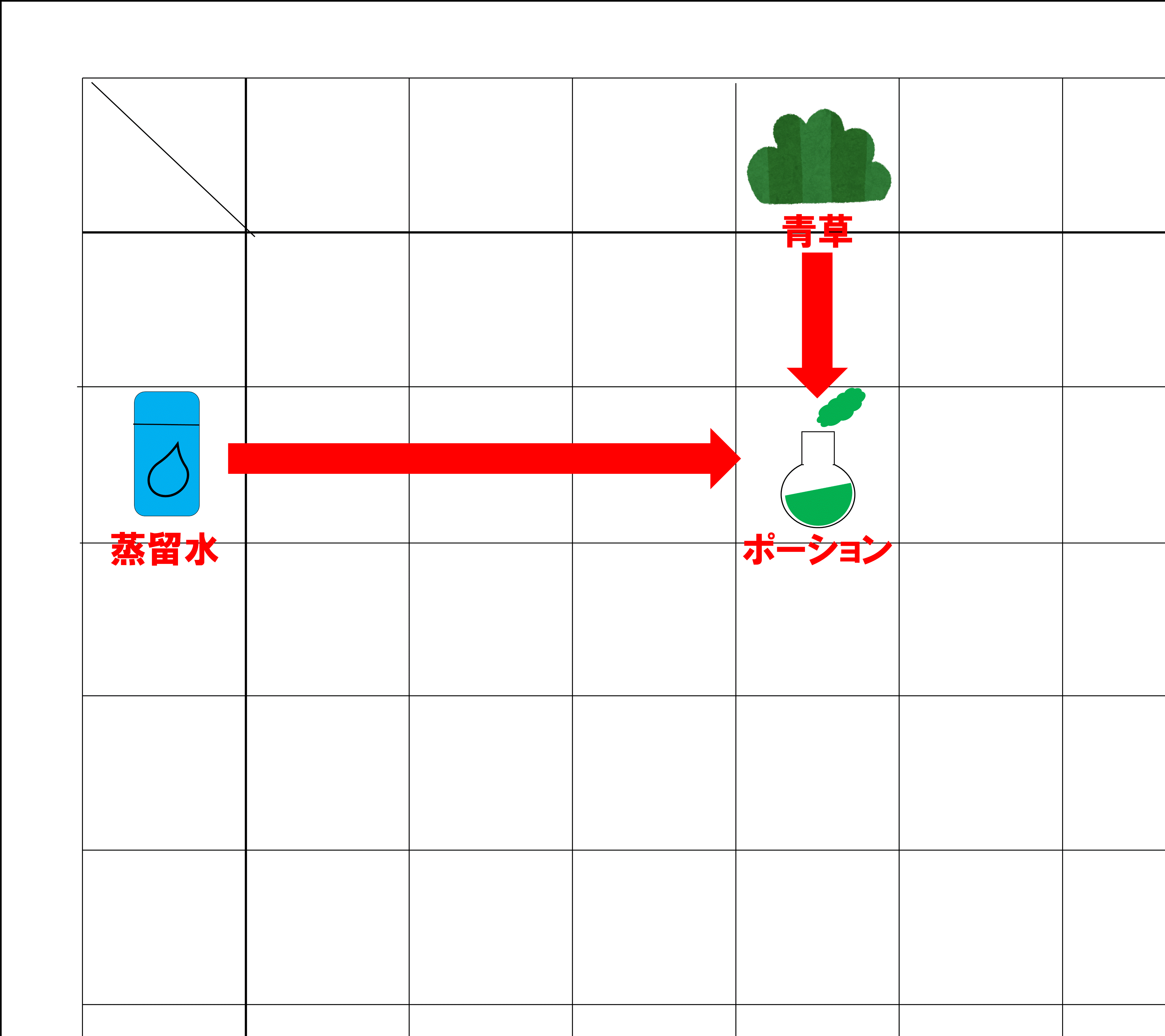『青草』と『蒸留水』を合成すると、『ポーション』を生成される。
ここで一つ疑問が生じました。
「質問だけど、さっきの例だと上から『青草』、左から『蒸留水』を選んでいたけど、これ逆だったら違うものが生成されんの？」
「そこ、大事。２枚の合成では、入れた順番は関係なし。」
「つまり、さっきは『青草』、『蒸留水』の順番に考えたけど、逆にして『蒸留水』、『青草』の順で合成しても同じ結果になるわけだ。」
「そう、結果が一緒になりたいから、表もそうしている。」
「【合成テーブル】の一番上・一番左それぞれに『青草』も『蒸留水』もあって、合成の順番を変えても結果が変わらないように、初めから【合成テーブル】には書かれているのか。」
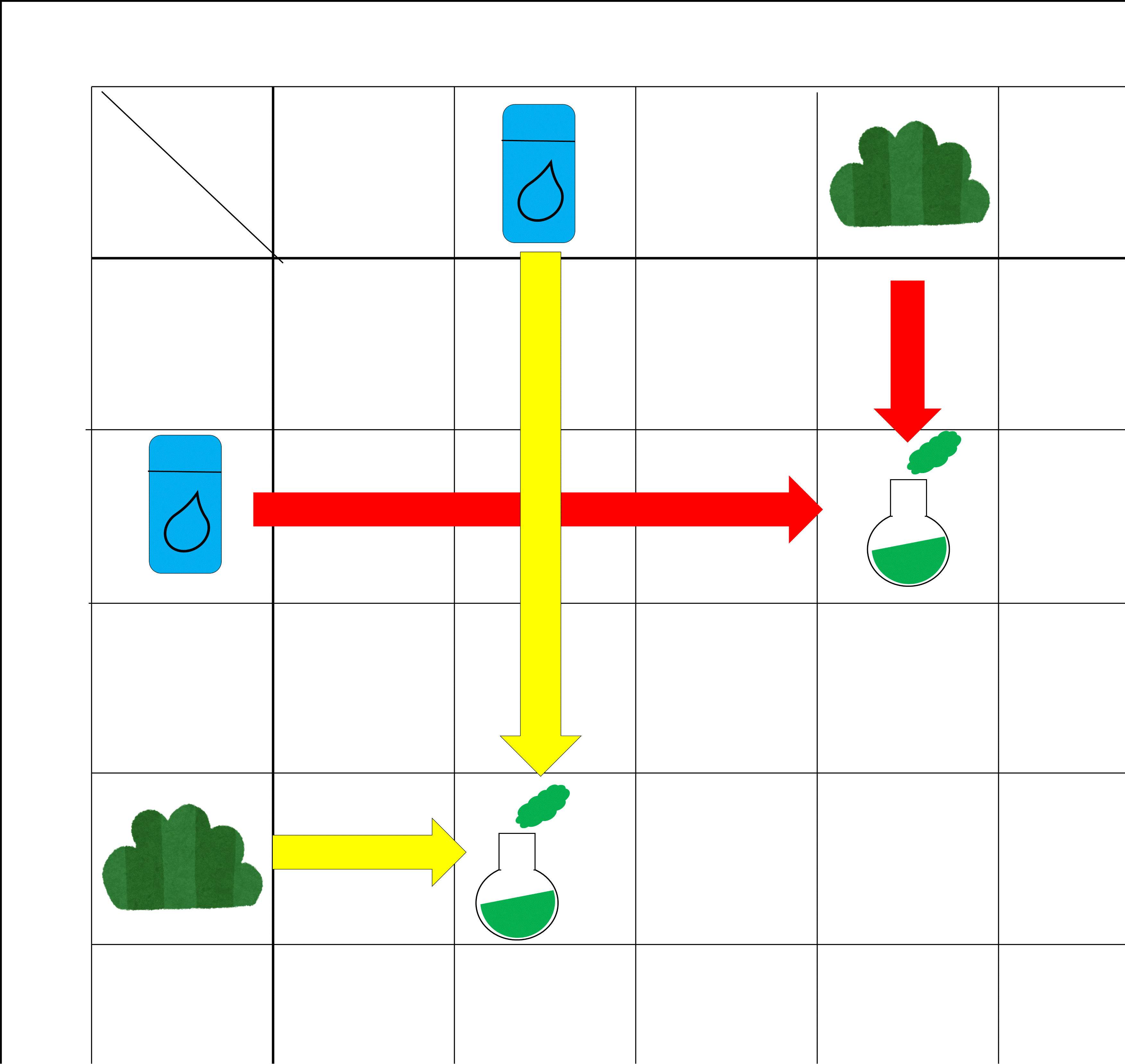２枚のカードの合成は順番を逆にしてもいい。
ここで上の会話の内容を、式を使ってまとめてみたいと思います。
見やすい式にするために、素材カード達をA,B,C,D,...とアルファベットで表しておきます。
素材カードA,Bの合成から、【合成テーブル】に基づいて素材カードCを生成することを次のように表す。
$$ \triangleright (A , B) ⇒ C $$
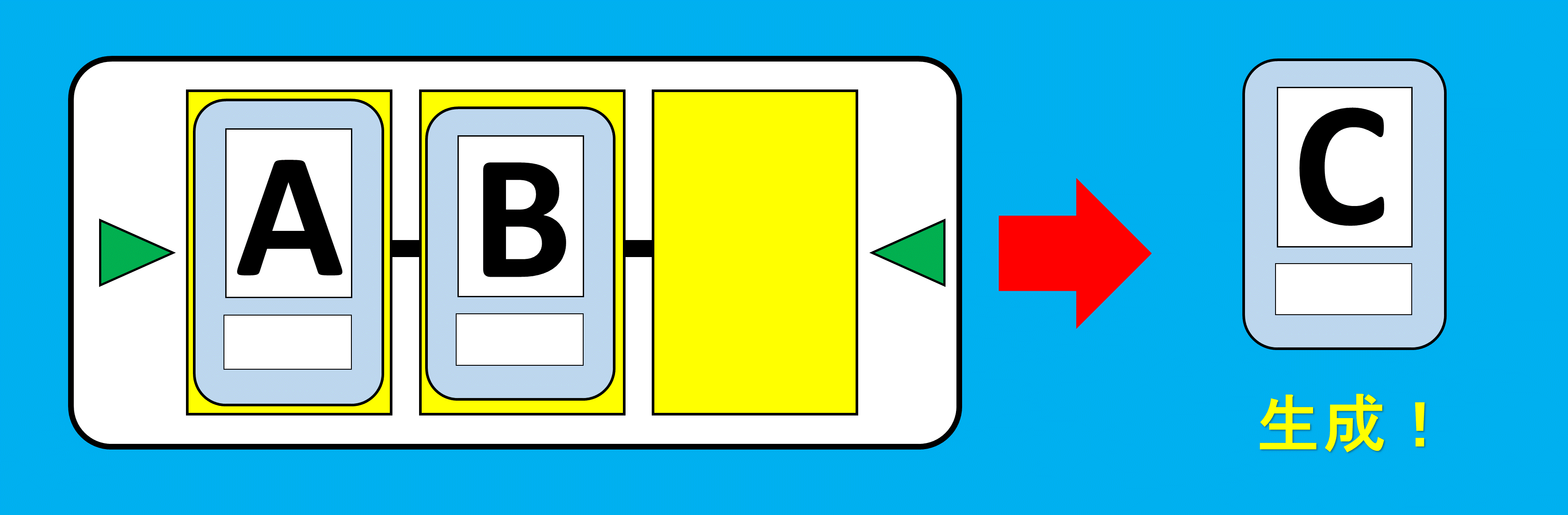AとBからCを生成する
この式は、( )のなかに合成する素材カードが入り、 ▷が合成する方向（つまり、一枚目を左のカード、２枚目を右のカードとしている）、そして⇒が合成を表して、その右隣に生成されるカードを置きます。
合成の例として登場した、『青草』と『蒸留水』を合成すると『ポーション』が生成される、という規則を記号で表すと、
$$
\triangleright (青草 , 蒸留水) ⇒ ポーション
$$
となります。
『青草』と『蒸留水』から『ポーション』を生成した。
素材カードA,Bの合成から生成される素材カードと、素材カードC,Dの合成から生成される素材カードが同じものになるルールを次のように表す。
$$ \triangleright (A , B) = \triangleright (C , D) $$
上の二つの定義を合わせると、
$$
\triangleright (A , B) ⇒ E かつ
\triangleright (C , D) ⇒ E ⇔ \triangleright(A , B) = \triangleright(C , D)
$$
となります。
これらの記号を使って、先ほどの会話の中で話されたルールを式にすると次のようになります。
$$ \triangleright (A , B) = \triangleright (B , A) $$
このルールは、合成結果を含めると、
$$
\triangleright (A , B) ⇒ C かつ \triangleright (B , A) ⇒ C
$$
ということを表しています。
このように合成と生成を式を使って表し、すっきりした見た目にして考えることができました。
「【合成テーブル】には、規則があるのか。他には？」
「あと、ダブル合成したとき、3つ合成したときがある。」
「それぞれ、どのような規則か教えてくれ。」
「まずはダブル合成。これ、同じ二つを合成することだけど、これするとかならず失敗して『ごみ』ができる。合成は複数の種類を混ぜてこそ。単一のものだけでは合成とはさせたくない。」
「・・・それで『ごみ』は、何か他で活用できたりするの？」
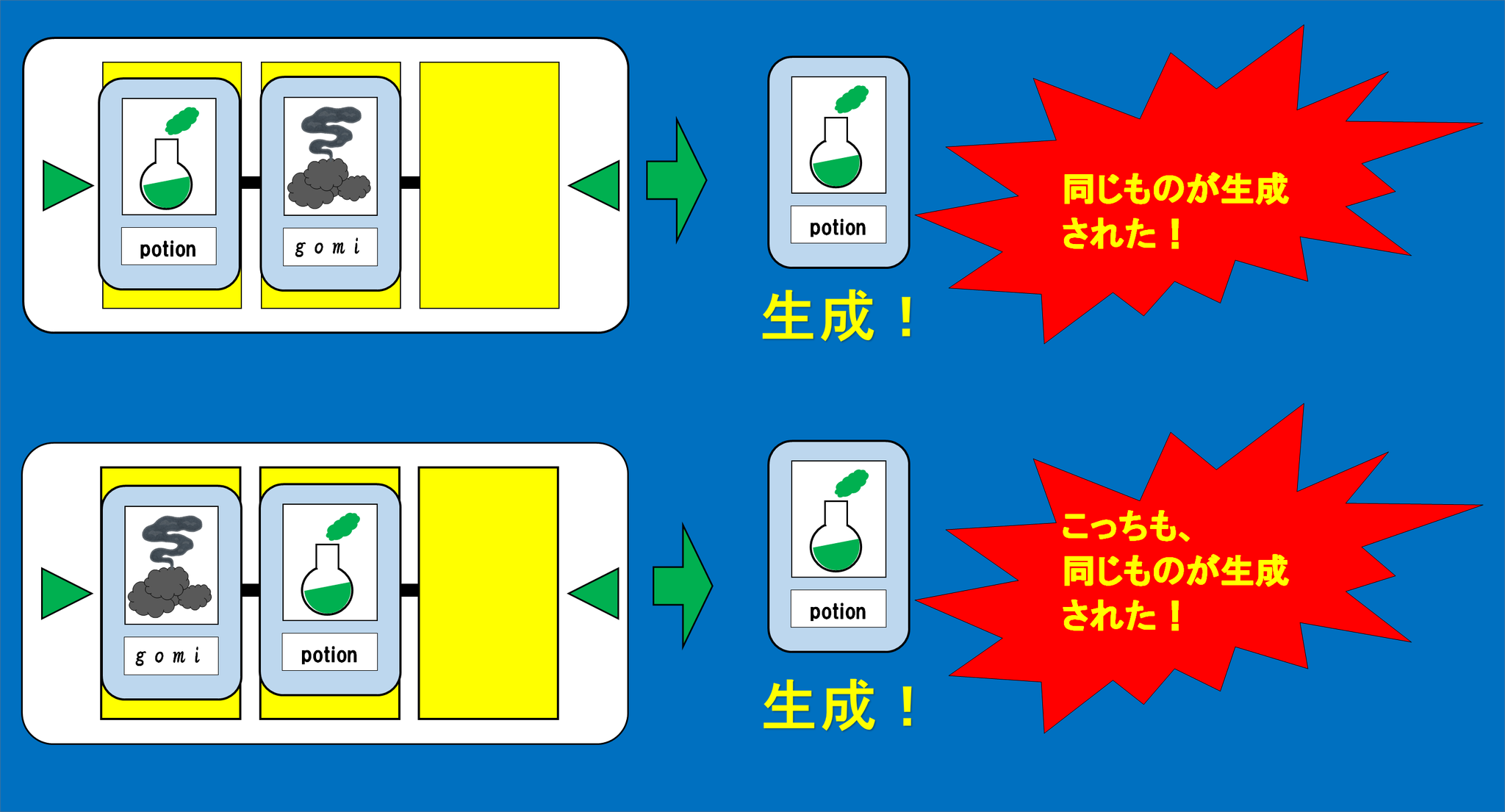
「いやむり。ほかのどんな素材カードも、『ごみ』と合成すると元の素材カードがそのまま生成される。」
「『ごみ』同士を合成すると？」
「『ごみ』一個が出来る。」
「なるほど・・・。じゃあ、三つ合成するときの規則というのはなんだ？ 確かに、場には3枚までカードが出せるルールのようだが。」
「三つのカードから一つのカードを生成したいけど、【合成テーブル】にあるのは二つのカードの合成。
三つのカードの合成は、左から二つを合成、そして生成したカードと残った一つを合成。これで三つから一つを生成可能。」
3つのカードの合成
「三つのカードを合成するときは、二つずつ合成するのか。それで、三つを合成したとき用の表をわざわざ作らなくて済むんだな。 えっと、三つ合成するときの規則っていうのはこれのことかい？」
「ん、ここからが大事。実際の合成で、初め二つを右からとるのか左からとるのか分かんなくなることがあった。だから、左右どちらから二つをとりはじめても、最後の結果が同じになるように表を作ることにした。」
「・・・その規則、結構面倒じゃない？つまり、三つのカードの合成を行うときに、
・まず左の二つのカードを合成して、そこから生成されたカードと右端の残りの一枚を合成
・まず右の二つのカードを合成して、そこから生成されたカードと左端の残りの一枚を合成
の二つの合成の仕方でそれぞれできる生成カードが同じ種類のカードになるように、表を作るってことでしょう？しかも、任意のカード三つに対して成り立つ！」
「でも、ストレスなくゲームができることが最優先。ユーザビリティ。」
「なるほどなぁ。・・・あっ、ここまでの規則を使えば、三つのカードの合成は、真ん中のカードから始めても結果が同じになることも分かるね。なるほどね。」
「？？？」
ここまでで登場した規則をまとめてみましょう。
まずは『ごみ』というカードの特徴から見てみます。
gを素材カード『ごみ』とする。
Aを任意の素材カードとするとき、
$$
\triangleright (A , g) ⇒ A
$$
$$
\triangleright (g , A) ⇒ A
$$
（どんな素材カードでも、『ごみ』と合成すると元のカードが生成される。）
$$
\triangleright (g , g) ⇒ g
$$
（『ごみ』同士を合成すると、『ごみ』が生成される。）
『ごみ』のカード。
『ごみ』と合成する場合の規則
『ごみ』同士を合成すると？
Aを任意の素材カードとして、
gを『ごみ』とすると、
$$ \triangleright (A , A) ⇒ g $$
が成り立つ。
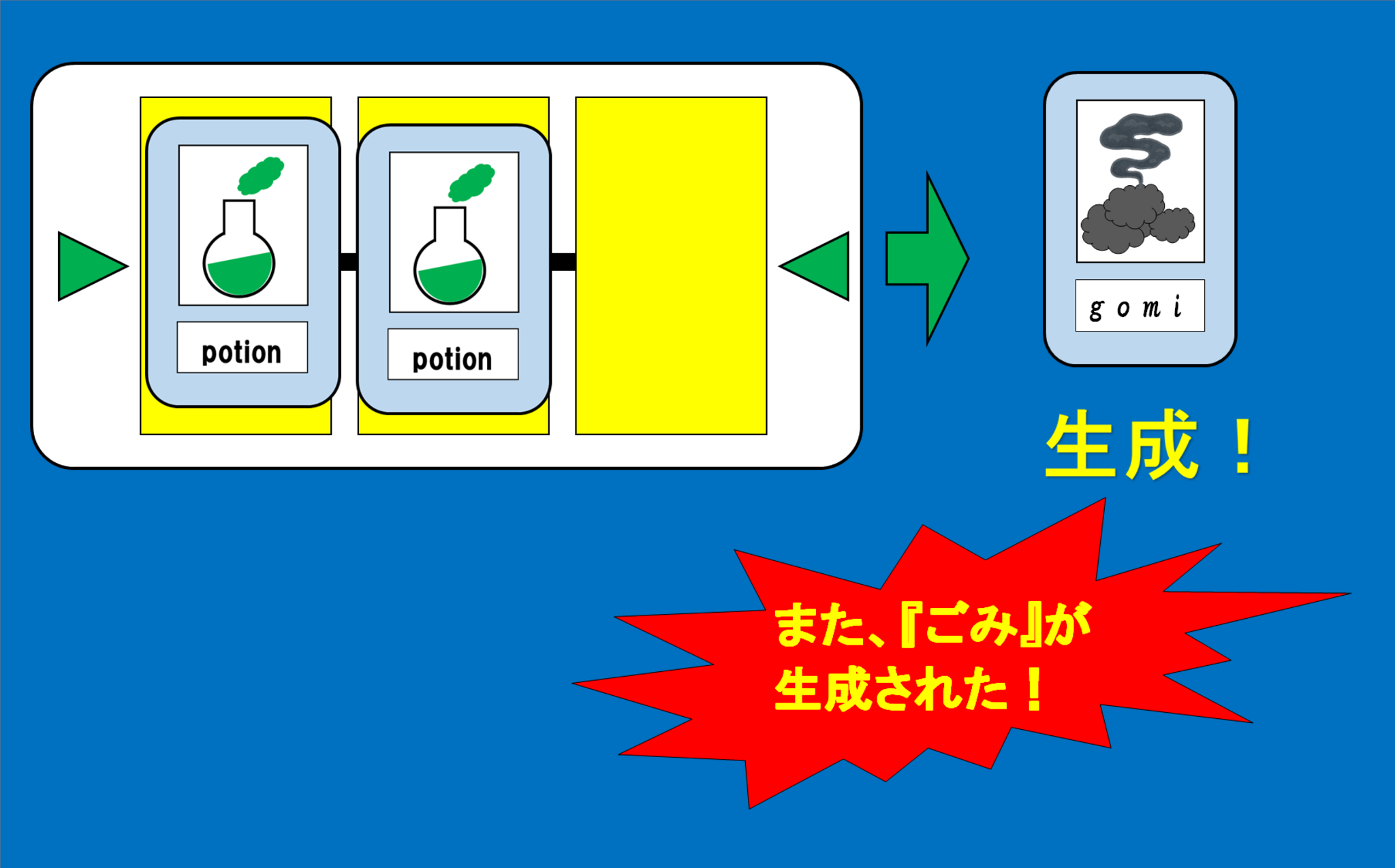ダブル合成をすると『ごみ』が生成される
次に三つの合成についての規則を、式を使って表します。
これまでは二つのカードの合成でしたが、ここからは三つのカードの合成について考えていきます。
二つのカードの合成よりも複雑なルールにはなりますが、式の見た目はあまり変わりません。
三つの素材カードA,B,Cを合成して、素材カードDを生成することを、
$$
\triangleright ( A , B , C ) ⇒ D
$$
と表す。
ここで一番重要なポイントは、三つの素材カードはいっぺんに合成するのではなく、実際は左から二つずつ順番に合成をするということです。
もう少し詳しく言うと、定義に書かれている式
$$
\triangleright ( A , B , C ) ⇒ D
$$
で表される合成を行うとき、GMはまず左の二枚であるAとBの合成を考えます。つまり、
$$
\triangleright (A , B ) ⇒ E
$$
を行います。
次に、GMはここで生成された素材カードEと、のこった素材カードCを合成します。つまり、
$$
\triangleright ( E , C ) ⇒ D
$$
を行います。
これで、場に出された３枚の素材カードは全て合成されて、一枚のカードDが生成されました。
この合成の流れを図で書いたものが下の図になります。
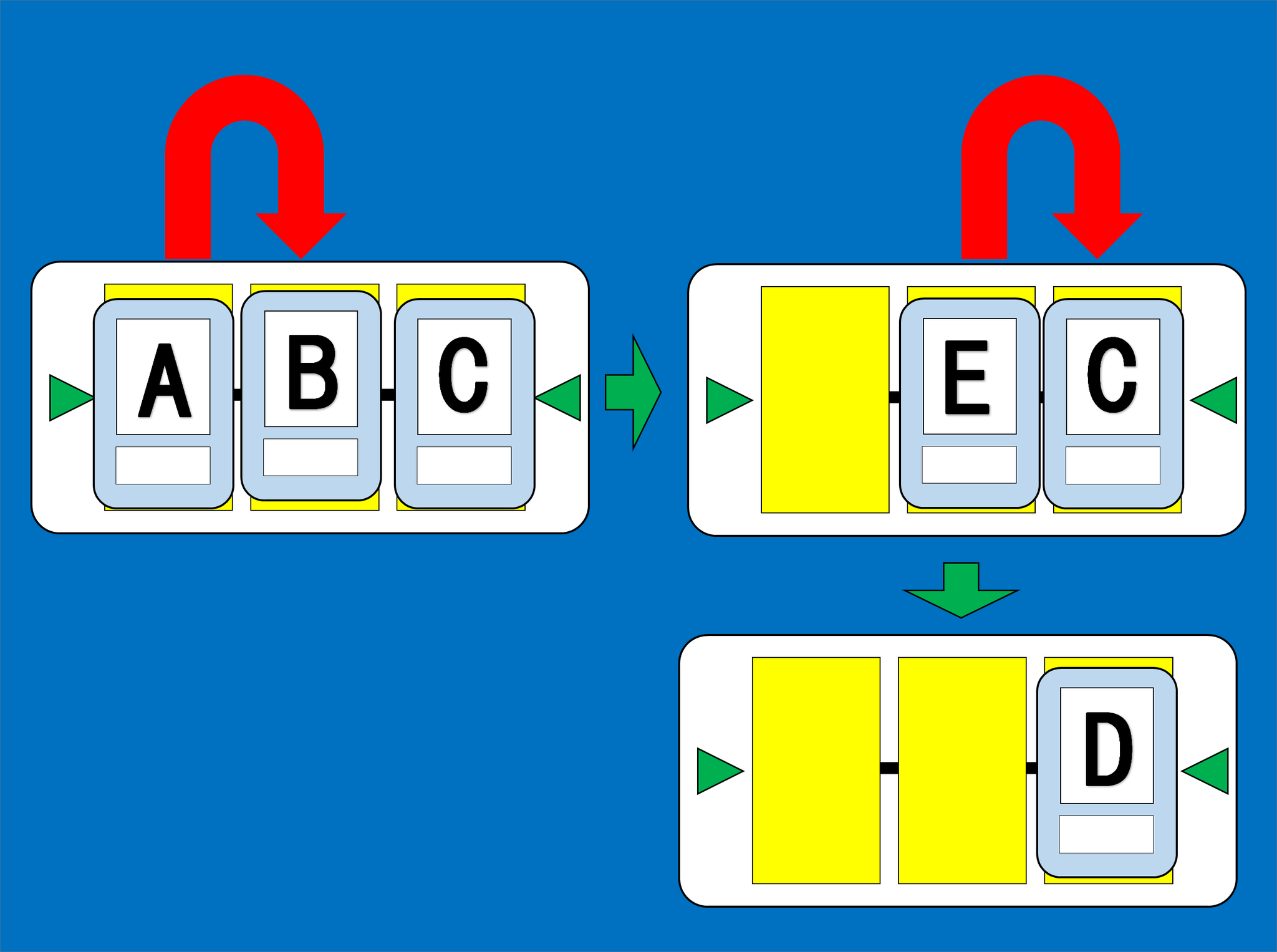3つのカードの合成
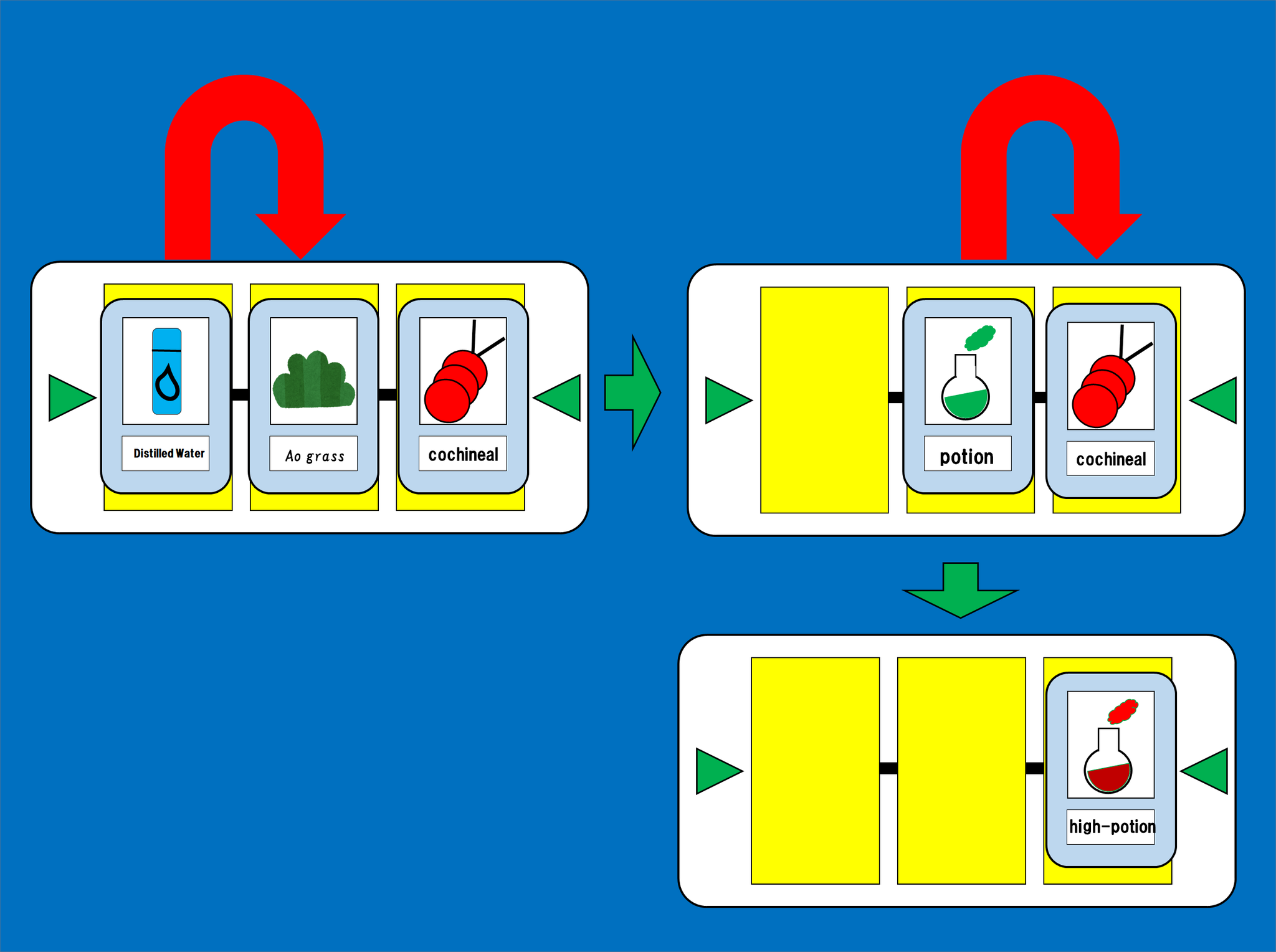
さて、この三つのカードの合成にも規則がありました。左右どちらから合成を始めたとしても、生成されるものがおなじになるというものです。この規則を式であらわすために、これまでとは逆方向に合成する、ということを記号で表していきます。
三つの素材カードA,B,Cを右から合成して、素材カードを生成することを、
$$
(A,B,C)\triangleleft ⇒ D
$$
と表す。
２枚のカードの合成の時に、二通りの合成方法が同じ結果になる、ということを＝で表しました。同じものを使って、今回の規則を式で表してみます。
$$ \triangleright(A,B,C) = (A,B,C)\triangleleft $$
（２枚のカードの合成の場合も、同じような規則が成り立つ。つまり、
$$
\triangleright( A , B ) = ( A , B )\triangleleft
$$
も成り立つ。）
この規則がとてもややこしいものだと会話の中では言っていましたが、下の図を見てみるとその理由が分かるかもしれません。
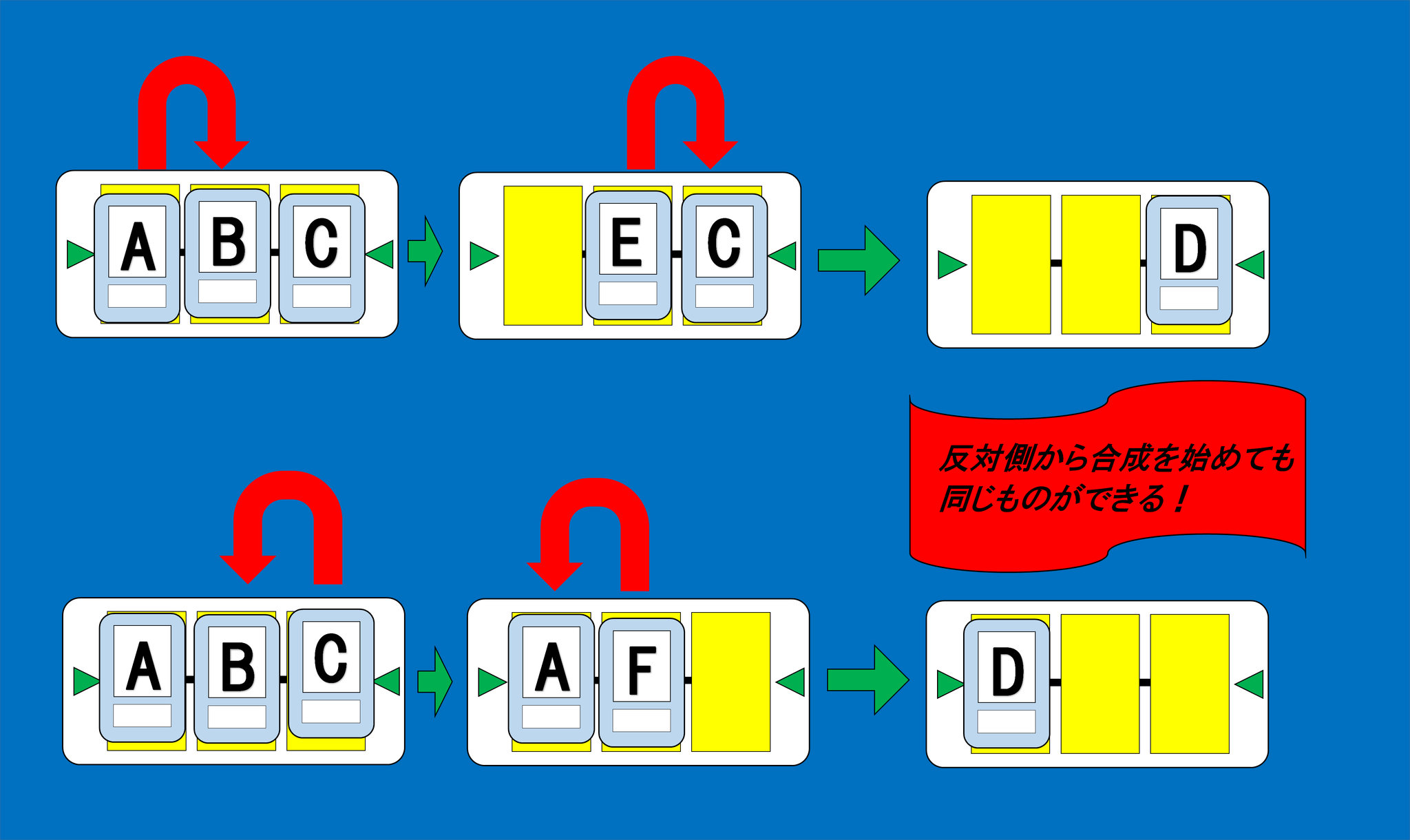反対側からの合成でも同じものができる
左側から始めた合成では素材カードＥとＣの合成により素材カードＤが生成されており、右側から始めた合成では素材カードＡとＦの合成により素材カードＤが生成されております。
つまり、全然違う種類の素材カード達から同じ素材カードが生成されていることになります。異なる種類の素材カード達の合成であっても、上の規則が成り立っているかを考えなくてはならない、ということになります。
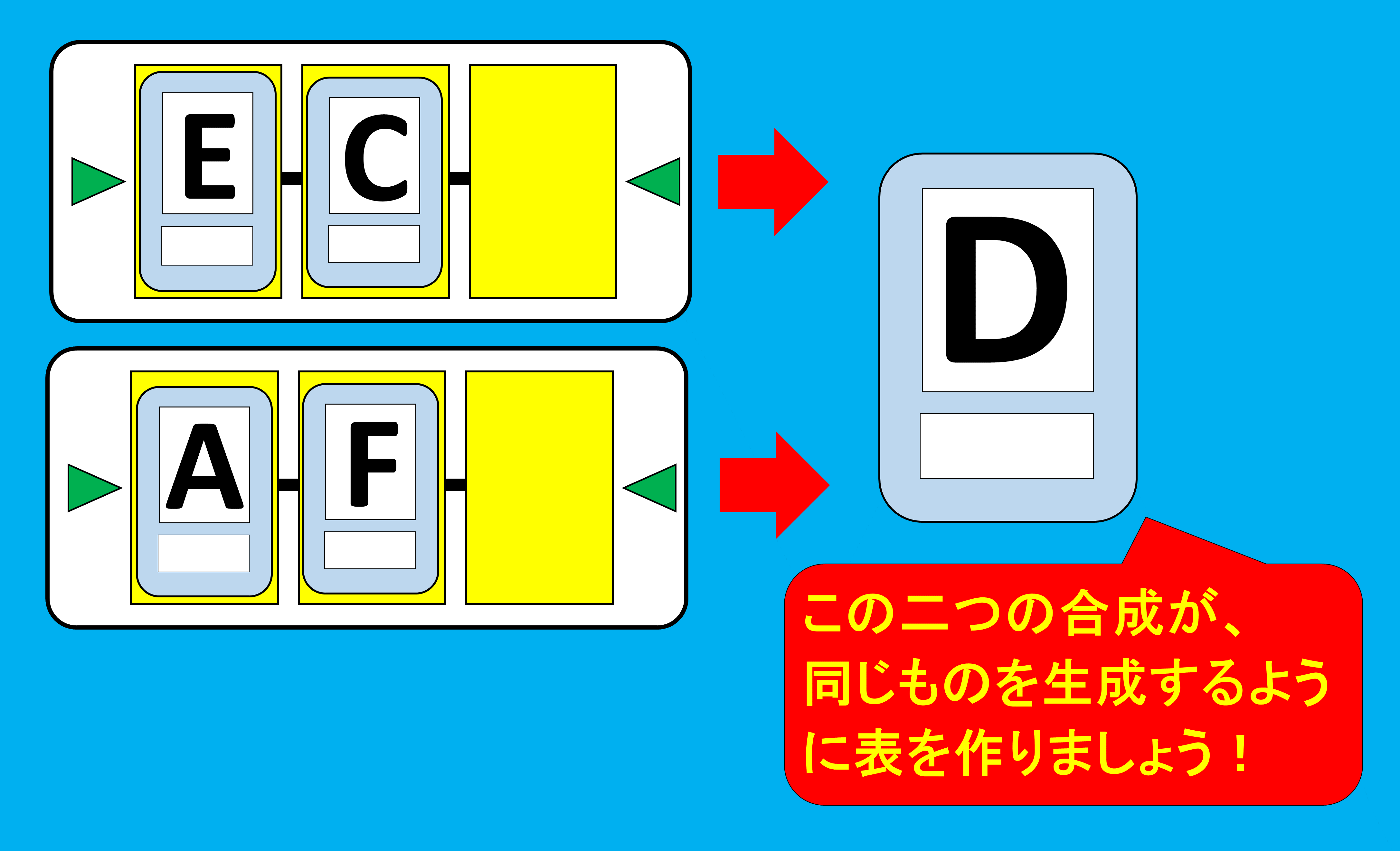上の例の場合、この二つの合成は同じものを生成する必要がある。
定義から新しく発見された規則
ここまでが作成者が意図して決めた【合成テーブル】の規則となります。しかし、あなたは会話の中で新たな規則を発見をします。場の真ん中から合成を始めても、端から合成を始めた場合と必ず同じ結果になる、という規則です。
このことを図を使って示してみましょう。
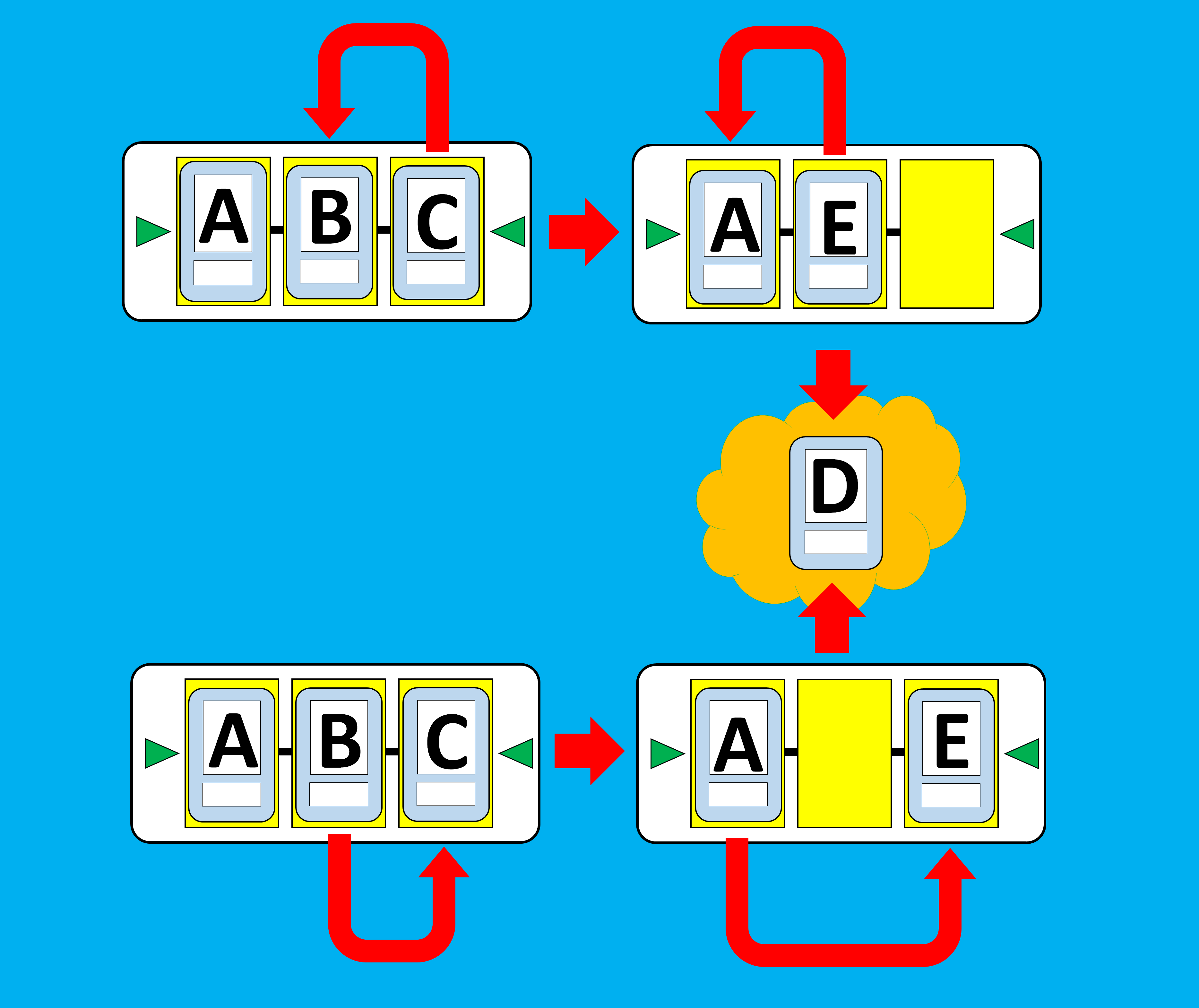真ん中からの合成はどうなるの？
まず、右から合成していく場合をみてみましょう。一枚目をC、二枚目をBとして合成し、素材カードEが生成されます。そして、このカードEとAを合成してDが生成されています。
この一連の合成を式で表してみると、次のようになります。
$$
( B , C )\triangleleft ⇒ E
$$
$$
( A , E )\triangleleft ⇒ D
$$
一方で、真ん中の素材カードBを一枚目、右端のカードCを二枚目として合成すると、何が生成されるでしょうか。
この合成を式で表してみると、
$$
\triangleright( B , C ) ⇒ ?
$$
（？にどの素材カードが入るのかは、まだ分かっていない。）
となりますが、前に登場した規則である、
$$
\triangleright( B , C ) = ( B , C )\triangleleft
$$
を使うと、
$$
( B , C )\triangleleft ⇒ E
$$
より、
$$
\triangleright( B , C ) ⇒ E
$$
であることが分かります。
そして、場にある素材カードはAとEの二枚になります。ここでも上と同じ規則により、
$$ \triangleright( A , E ) = ( A , E )\triangleleft $$
であるので、どちらを選んでも合成結果はDとなります。
つまり、右から順番に合成した場合と、真ん中から右に向かって合成を始めた場合が同じ合成結果になるということが分かりました。
さて、真ん中から右に向かって合成した場合についてを考えましたが、同じように考えて真ん中から左に向かって合成した場合と左から順番に合成した場合も同じ合成結果になります。
さらに、定義より右から順番に合成した場合と、左から順番に合成した場合が同じ合成結果になるのでした。ここまでのはなしから、三枚の素材カードからとなり同士のカードを二枚どのように選び、どの向きから合成を始めても、最後に生成される素材カードは同じものになるということになります。
つまり、今までは合成する順番にこだわって式を作りましたが、最後に生成されるカードは、どの素材カードを場に出したかによって決定されるのであって、それらの合成する順番は関係ないということです。
場に出された素材カードによって最後に生成されるカードは、その合成の順番に関係ない。
この発見から、素材カードの合成を式で表した、
$$ \triangleright( A , B ) ⇒ C $$
などは、合成する方向を表している記号、
$$
\triangleright , \triangleleft
$$
が無駄であったと考えられます。
そこで、次はより簡潔に合成を表せる式を作ってみましょう！
合成の記号 パート２
新しい合成の式では、簡潔に表せるだけでなく、その合成が今まで登場した三つの合成のルールに則っていることがよく分かるような記号を使いたいとおもいます。
その記号とは、” + ”です。
A,B,Cをそれぞれ素材カードとする。
場に左から順にA,Bのカードが置かれ、左から順にカードを合成し、素材カードCが生成されることを、
A + B = C
と表す。
また、場に左から順にA,B,Cのカードが置かれ、左から順にカードを合成し、素材カードDが生成されることを、
A + B + C = D
と表す。
素材カードA,Bを合成することで生成されるカードと、素材カードD,Eを合成することで生成されるカードが同じものになることを次のように表す。
A + B = D + E
また、素材カードが三枚ずつある場合も、同様の式で表す。
A + B + C = D + E + F
素材カードA,Bの合成について、次の式が成り立つ。
A + B = B + A
素材カード『ごみ』をgで表すと、このカードの合成は次の式が成り立つ。
A + A = g
A + g = A
g + g = g
素材カードA,B,Cの合成について、B,Cの合成を先に行い、生成されたカードとAを合成するという順番で合成することを、次の式で表す。
A + ( B + C )
またこの定義に合わせて、A,Bの合成を先に行い、生成されたカードとCを合成することを次の式で表す。
( A + B ) + C
A,B,Cをそれぞれ素材カードとするとき、
( A + B ) + C = A + ( B + C )
最後の定義に登場した"+"の式は、▷、◁ などの記号で表していたときの式と大きく変わっているように見えるかもしれませんが、これまでの話を参考にすると、"+"の定義から出発しても、▷、◁の記号で表していた時の式での定義を再現することができます。
”+”を利用することで、より分かりやすい式になったのではないでしょうか。
次の【問題編】では、この”+”を使っていきます。
ここで【設定編】は終わりです。ここまでに登場した【合成テーブル】の規則から、どのような問題が現れるのでしょうか？
もし後の問題が気になってくださったならば、この記事の続きである下の記事を是非ご覧ください！
この記事を高評価した人
この記事に送られたバッジ
投稿者
