嘘か真か？位数２の元からなる可換群の位数は２の累乗！？ 《問題編》
はじめに
実は、こちらの記事は『前編』『後編』でいうところの『後編』にあたります。
『前編』にあたる記事をまだ読んでいない方は、下の記事を先に読むことをおすすめします！
≪設定編≫に登場したルール一覧
前編のラストに登場した【合成テーブル】の規則の一覧がこちらにあります。
（必要な時にタブを開いて確認してください。）
定義１ 合成を表す記号
A,B,Cをそれぞれ素材カードとする。
〈素材置き場〉に、左からA,B,Cの順にカードが置かれ、左から順に合成し、素材カードDが生成されることを、
A + B + C = D
と表す。
また、〈素材置き場〉に先ほどと同じようにカードが置かれ、B,Cを初めに合成して、生成したカードをAに合成する操作を、次のように表す。
A + ( B + C ) = D
定義２ ２通りの合成
素材カードA,B,Cを合成することで生成されるカードと、素材カードD,E,Fを合成することで生成されるカードが同じものになることを次のようにあらわす
A + B + C = D + E + F
定義３ 二つのカードの合成
素材カードA,Bの合成について、次の式が成り立つ。
A + B = B + A
定義４ 『ごみ』というカード
素材カード『ごみ』というカードをgで表すと、このカードの合成は次の式が成り立つ。
A + A = g
A + g = A
g + g = g
定義５ 合成の順番を表す記号
素材カードA,B,Cの合成について、B,Cの合成を先に行い、生成されたカードとAを合成するという順番で合成することを、次の式で表す。
A + ( B + C )
またこの定義に合わせて、A,Bの合成を先に行い、生成されたカードとCを合成することを次の式で表す。
( A + B ) + C
定義６ 三つのカードの合成の順番
A,B,Cをそれぞれ素材カードとするとき、
( A + B ) + C = A + ( B + C )
「それで、《問題》というのはなんだい？」
「うん、今は【合成テーブル】を実際に作成する段階なんだけど、ここで一つ問題があった。至急答えを出してほしい。
簡単に言うと、この表に載せられる素材カードの数が限られているみたい。」
「ん？表を縦横に広げていけば、表に載せられカードの種類をいくらでも増やせるじゃないか。」
「いや、カードの種類自体はいくらでも増やせる、と思う。ただ、その表にのせられない種類の個数がある…らしい。」
「たとえば？」
「例えば…、３枚のカードのみの【合成テーブル】とか。」
実際に、３種類の素材カードのみを載せた【合成テーブル】を作ってみましょう。
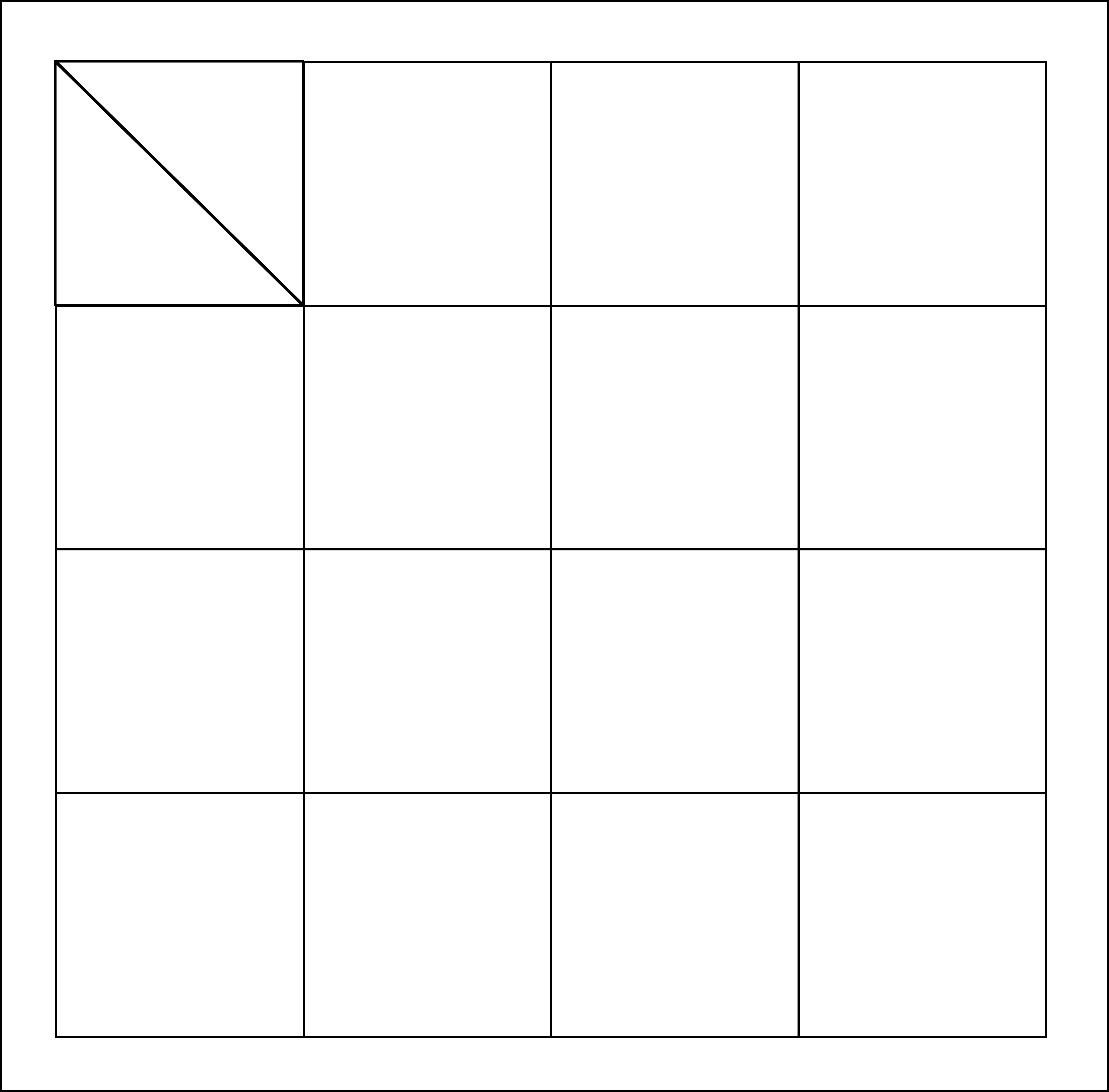3種の素材カードの合成テーブル
上の用紙が、３種類の素材カードのみが登場するゲームを想定して作られた【合成テーブル】です。
しかしまだ、素材カードが書かれていません。こちらを今から加えていきましょう。
合成結果を作ってみる
今回登場する素材カードは『青草』、『凡水』、『ごみ』の３種類です。
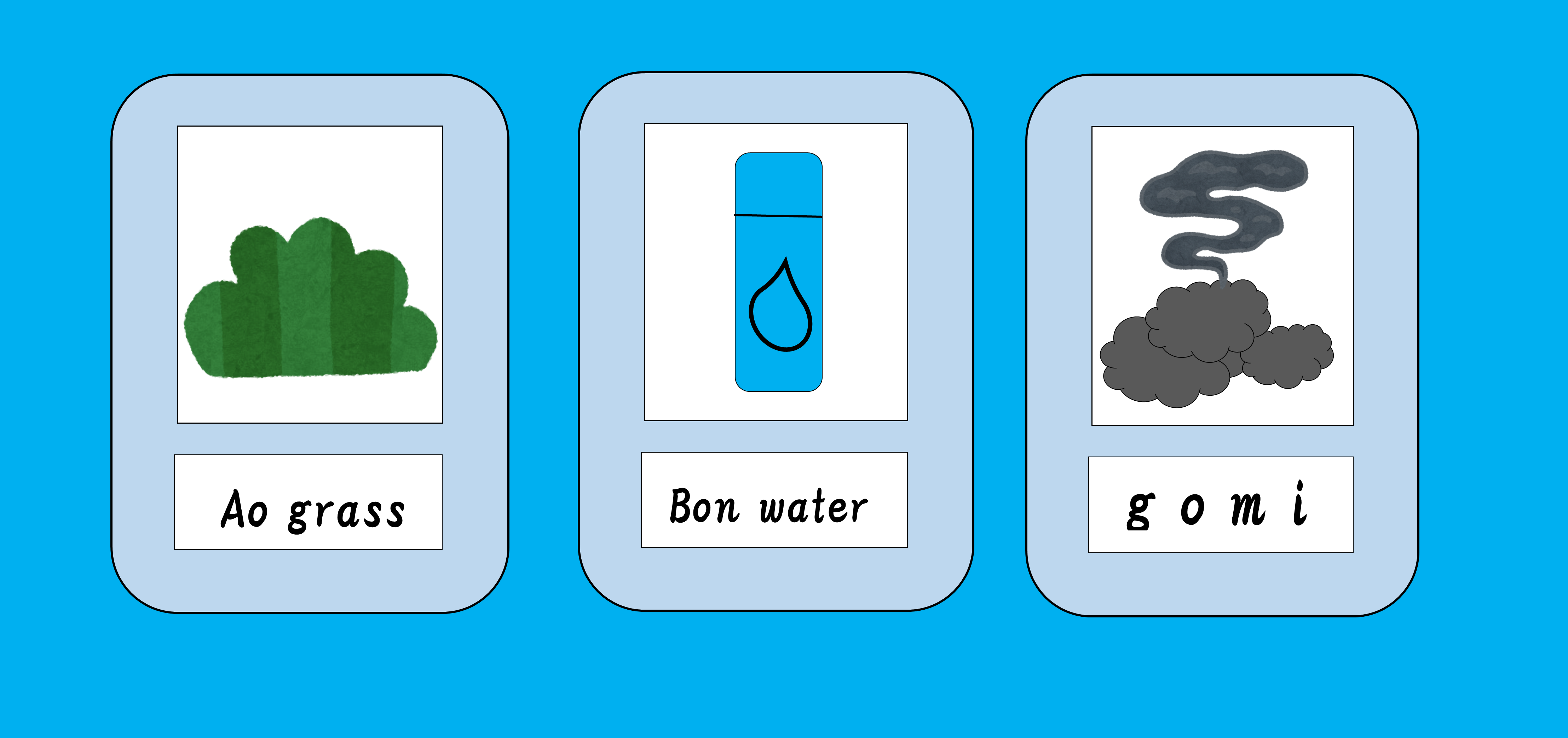3種類の素材カード
ここで、あらかじめこの3つの素材カードを記号で表しておきます。
『青草』: A ( Aokusa )
『凡水』: B ( Bon water )
『ごみ』: g ( gomi )
そして、【合成テーブル】の上一列と左一列にこれらを並べておきましょう。
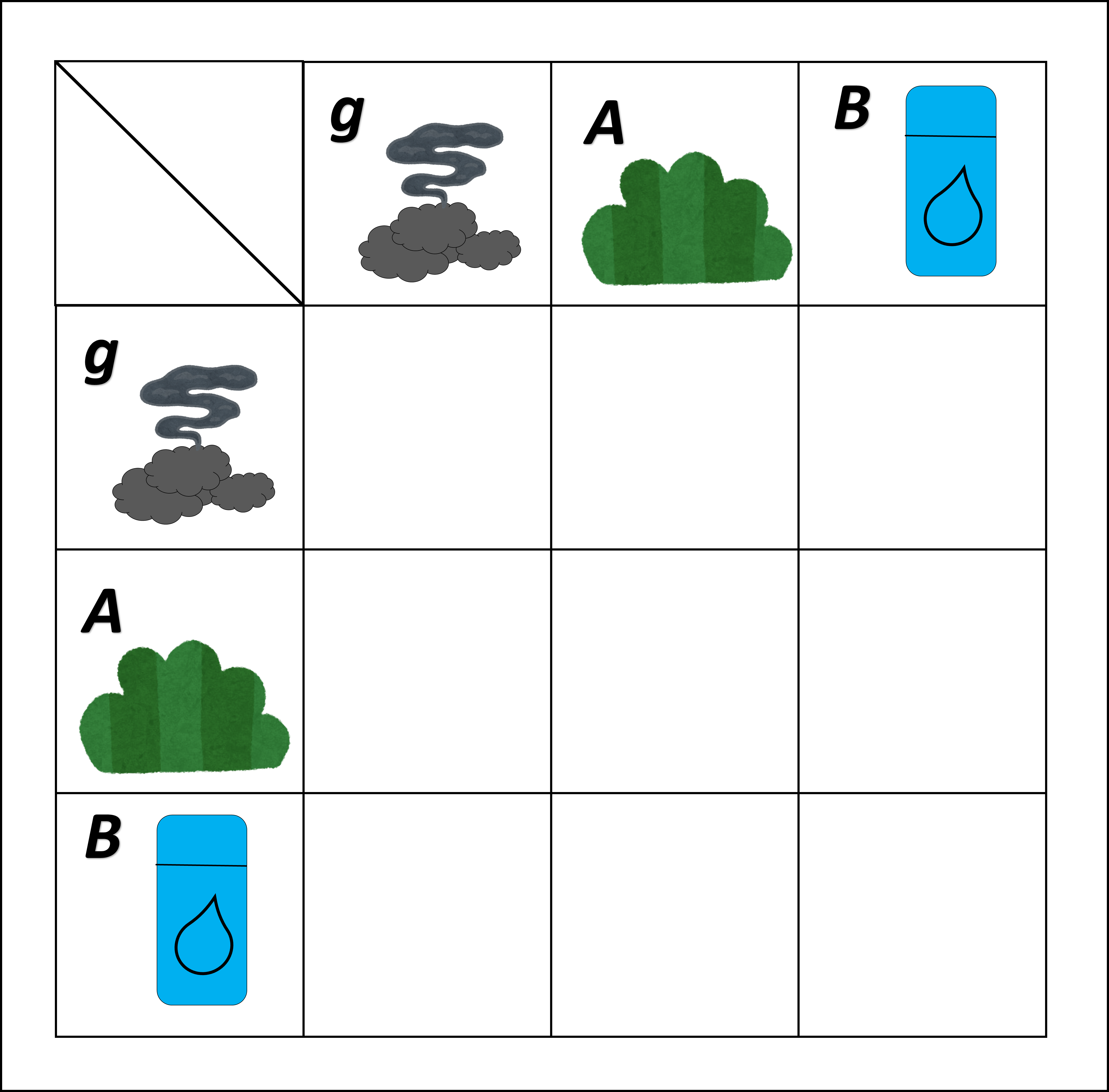合成テーブルの台ができた！
初めに、合成結果が確定しているところから表を埋めていきましょう。
素材カード達の中でも、『ごみ』は表の規則の中で特別な振る舞いをするカードでした。というのも、【定義５】より『ごみ』が関わる合成は、結果が決まったものになるからです。
まず、同じ素材カード同士の合成は『ごみ』を生成するので、
A + A = g
B + B = g
g + g = g
となります。
この合成結果を表に加えると、下の図のようになります。
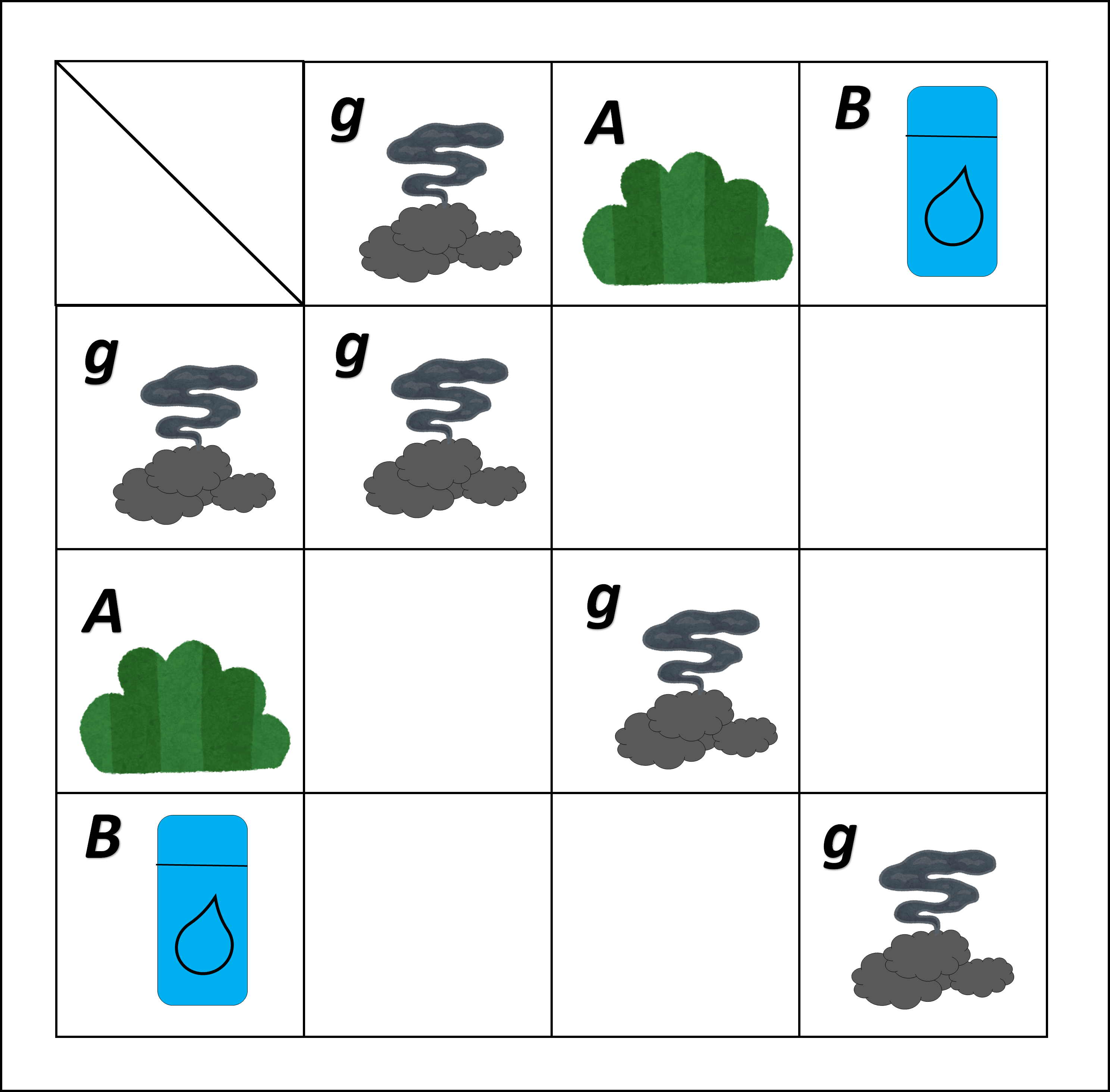ダブル合成の結果を入れた。
次に、ごみを合成する時の規則より、
A + g = A
B + g = B
g + A = A
g + B = B
となります。
先程の表にこれらの合成結果をさらに加えると、下の図のようになります。
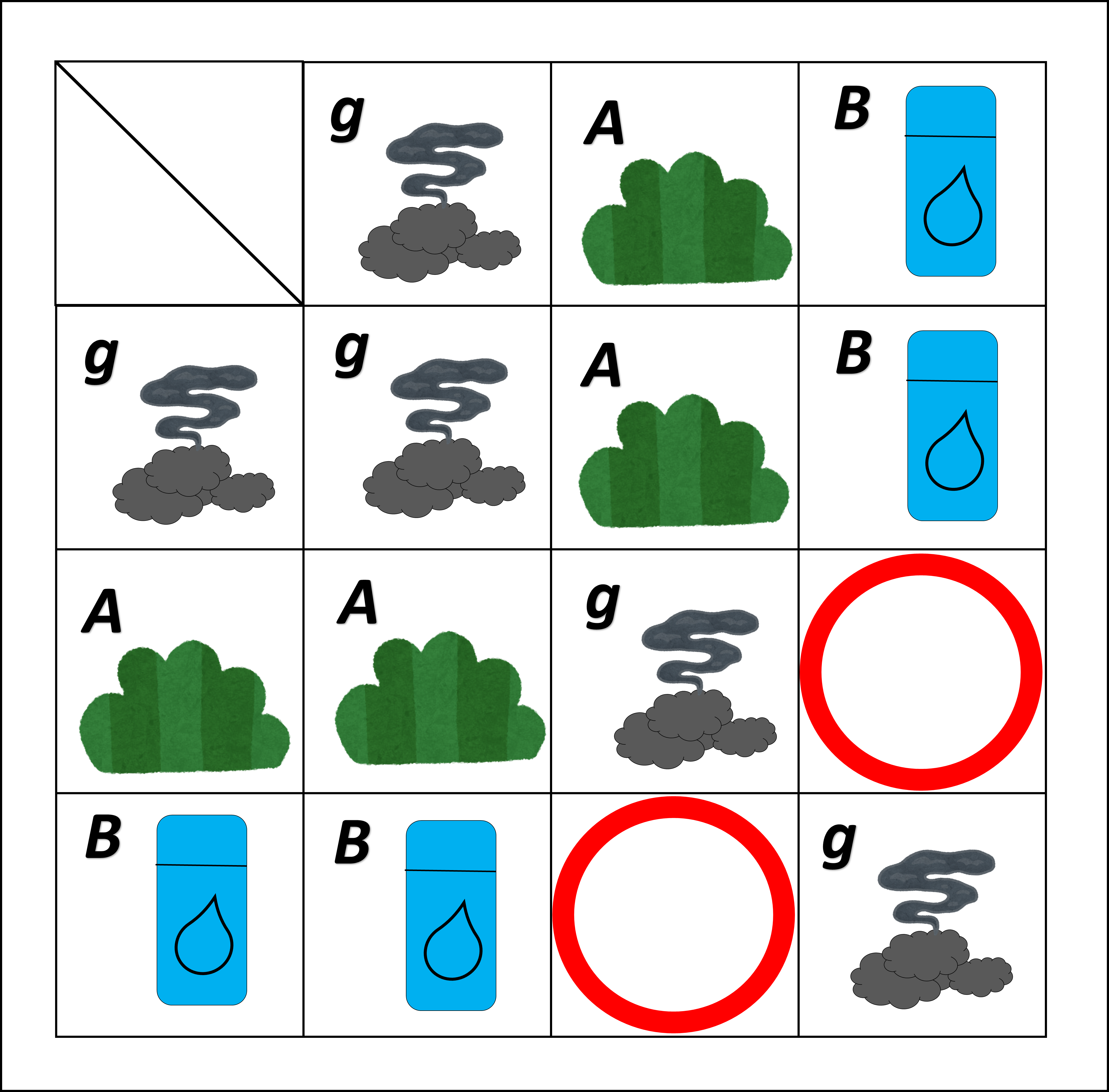空いているところはあと二つ！（〇があるところ。）
これで、【合成テーブル】の空きマスは残り二個になりました。ここまでは問題ありません。
しかし、ここからは結果が一通りとは限らない合成が登場します。残った二個の合成はそれぞれ次のような式で表されます。
A + B = ?
B + A = ?
２枚のカードを合成するときに、『順番を逆にしても合成結果は変わらない』という決まり（ A + B = B + A ）があったので、上の二つの式の結果は同じものにしなければなりません。
さて、これらの式の合成結果は今回登場している３種類のカードA,b,gのうちの１つです。どれでも一つ自由に選んで当てはめればいいような気がしますが、ここで三枚のカードを合成する際の規則（定義６）が自由をきつく縛ってきます。
まずは、合成結果がgになる場合で考えてみましょう。
A + B = g
B + A = g
（この二つの式の結果は必ず同じものになる。）
これらの式自体には問題がなさそうです。
これで一旦表が完成しますが、この表はしっかり【合成テーブル】の規則を守れているのでしょうか。
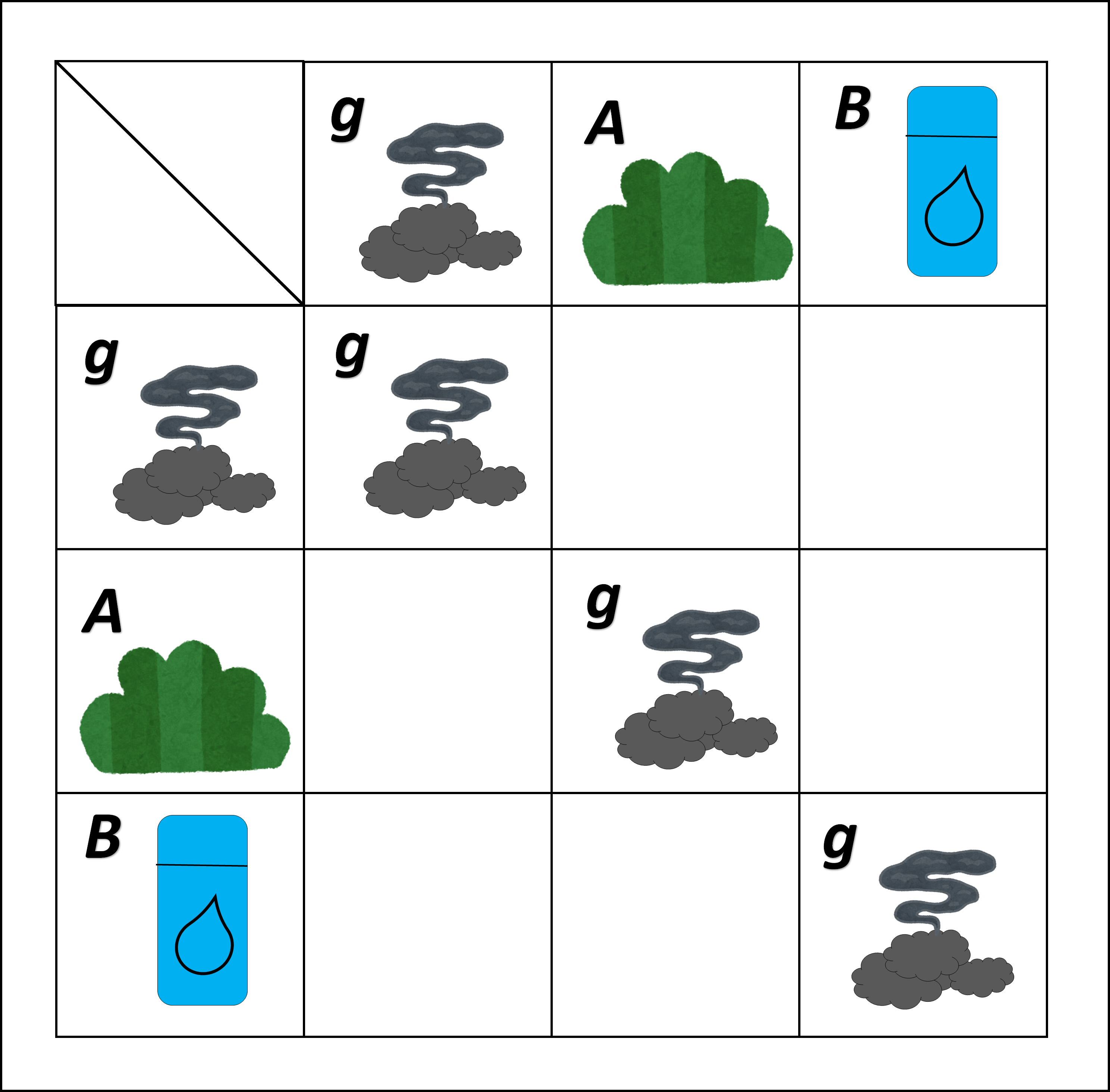これで完成か・・・？
次のように合成する場合を見てみましょう。
A + B + B = ?
この時、前から順に合成していくと、
( A + B ) + B
= g + B
= B
一方、後ろから合成をしていくと、
A + ( B + B )
= A + g
= A
となり、二つの合成の答えは違うものになってしまいました！
つまり、
( A + B ) + B $ \neq $ A + ( B + B )
となります。
この合成の式は【合成テーブル】の規則（定義６）に反しているので、この表はゲームに使うことができません。
さて、ここでルール違反が起きてしまったのは、先程決めたこの合成が原因とみてよいでしょう。
A + B = g
B + A = g
では、この二つの合成の結果を別のカードにした場合はどうなるでしょうか。
A + B = A
B + A = A
とおくと、どうなるか。
実は今回の場合でも、先程と同じような違反が起きてしまいます。
次の合成を使って示してみましょう。
A + A + B = ?
( A + A ) + B = A + ( A + B )
が成立するかどうかを確認してみると、
( A + A ) + B
= g + B
= B
A + ( A + B )
= A + A
=g
よって
( A + A ) + B $\neq$ A + ( A + B )
となり、今回の場合も【合成テーブル】の規則に反してしまいます。
最後に、次の式を受け入れるとしたら、どうでしょう？
A + B = B
B + A = B
この式も、【合成テーブル】の規則に反する式が作れてしまいます。
（上で示したことを参考に、ぜひ考えてみてください！）
ということで、式の答えになりうる三通りの場合をすべて見ていきましたが、どの場合も表の規則に対して違反が起きてしまいました。そして、作った三通りの表の他に考えられるものはないので、３種類の素材カードのみが書かれた【合成テーブル】はどうやっても作れない！と、いうことが言えます。
★問題★
先程は3種類の素材カードが載っている【合成テーブル】を作ろうとしてうまくいきませんでした。では、これが4種類のカードが載っているものになるとどうなるでしょう。
先程の問題点を踏まえて、４種類の素材カードのみが載っている【合成テーブル】を作ることができるでしょうか？
HINT! : ３種類のカードの【合成テーブル】の時は、合成結果を選択できた式は2つしかありませんでした。
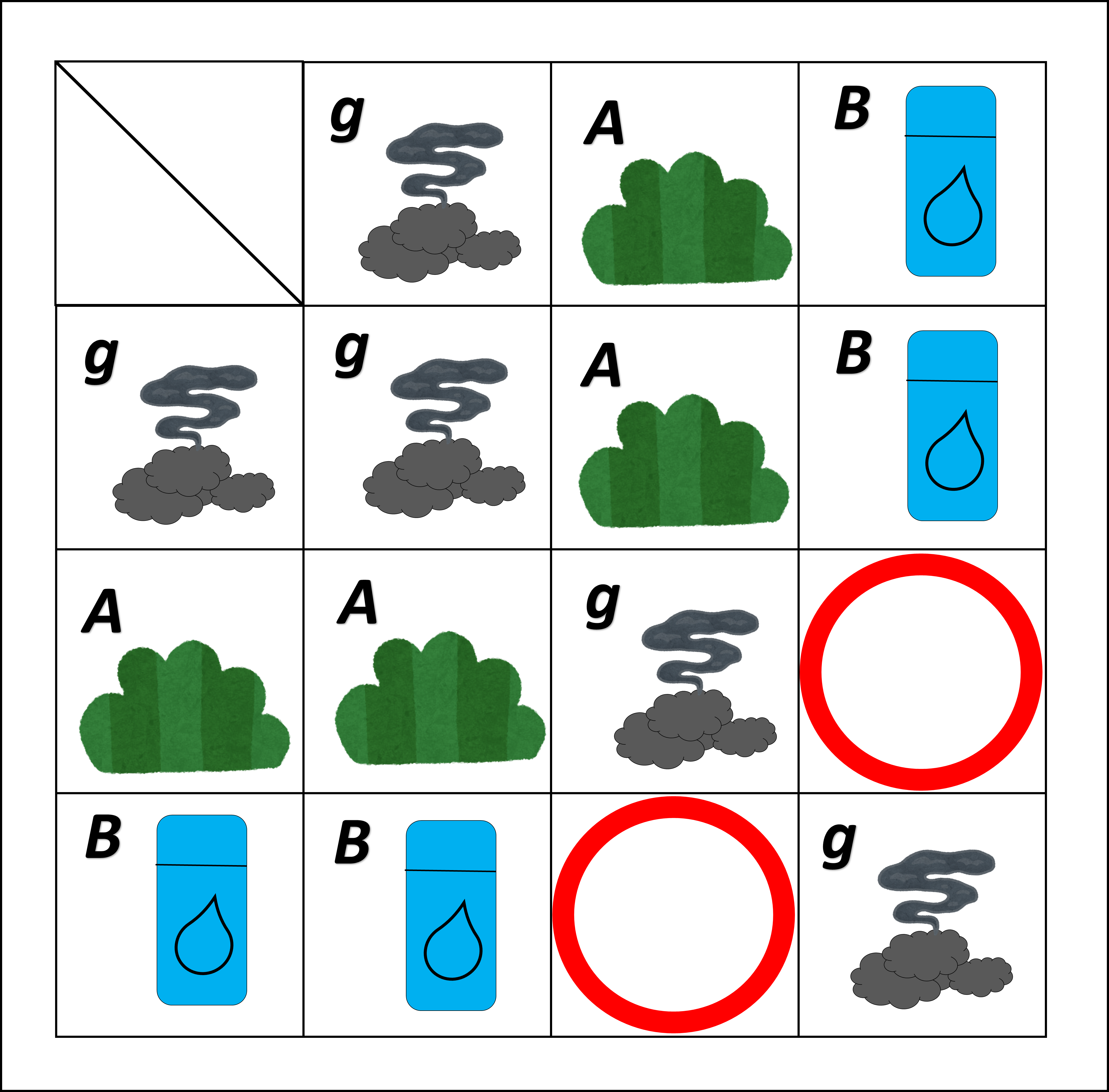この場合は２ヶ所だけ空いていた
４種類のカードの【合成テーブル】の場合だと、合成結果を選択できる式が６つあります。
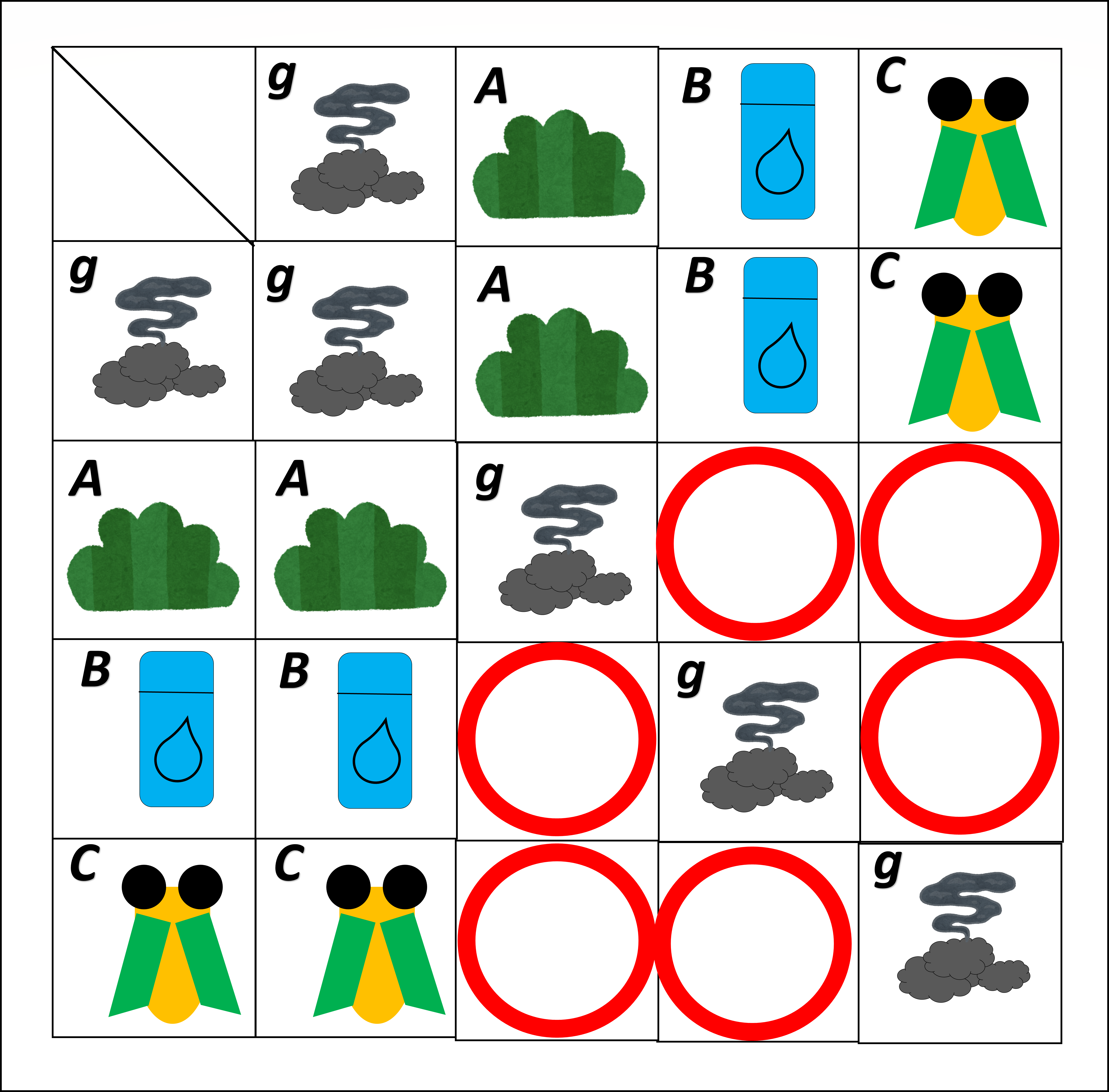4種類のカードの場合では6ヶ所も空いている！
まずはこれらの内から１つの式を選んで、合成結果を決めてみてください。すると、残りの５つのうち、実は合成の結果が１つに決まるものがいくつか登場するので、それを表に書き込んでみましょう。
.
.
.
4種類の素材カードの【合成テーブル】
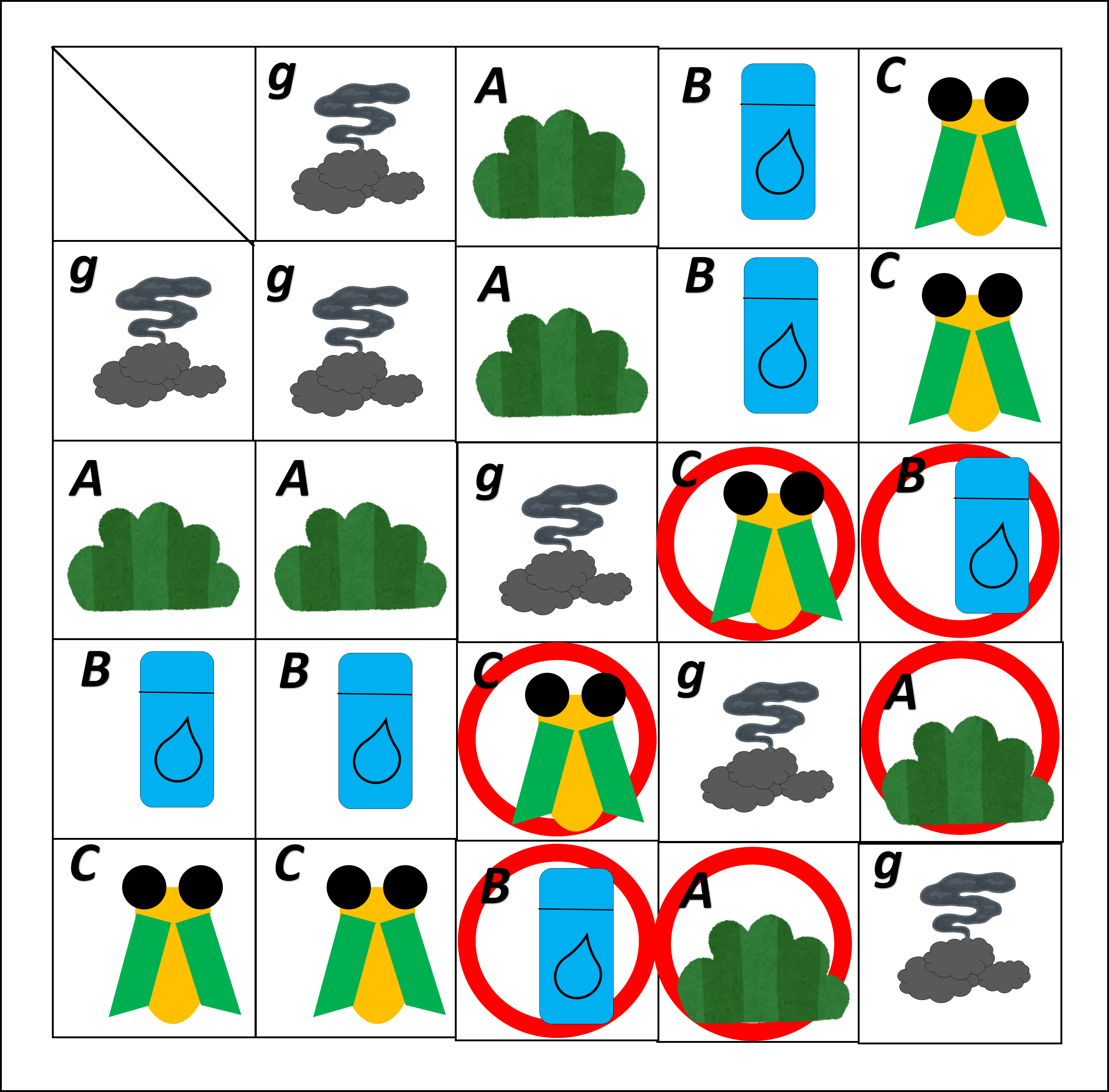完成！！
上の表が、４種類の素材カードの【合成テーブル】、つまり先程の問題の答えになります。
この表に沿って素材カードの合成を行えば、合成の規則に矛盾せず全ての合成を行うことができます。特に、三つの素材カードの合成の全通り（ 4×3×2 通り！）が規則を満たしていることが確認できます。
予想の登場
ここまでの話をまとめると、3種類のカードで構成された【合成テーブル】は作ることが出来ませんが、4種類のカードがあるものは作ることが出来る、ということでした。
「……というわけで、作れない【合成テーブル】がある。」
「3種類のカードだけだと表が出来ないけど、4種類のカードだと表が出来る。どうやっても規則に沿う表が出来ないカードの枚数があるのか……。出来るものと出来ないものを分けるような、何か法則はないのか？」
「……。実は、『予想』あり。ちょっとだけ調べたんだけど、表が出来るカードの種類の数に法則がありそう。表が出来るカードの枚数で、僕が見つけたものは小さい方から、
2、4、8、16
だったんだ。つまり……」
「つまり、カードの枚数が2の累乗なら、【合成テーブル】が作れる。」
「ん。で、カードの枚数がそれ以外なら、作れない...かも。きちんと確認はできてない。」
「ふーん。でも、大体答えが分かってるんじゃないか。もうそれを正解にしてさ、さっさと表を作っていけばいいと思うよ。カードの方はもうイラスト原案を書いてもらっているんだろ？」
「そう、そこ、そこが問題！素材カードのイラストをある高名な方に描いてもらった。多少値は張るが、うちの会社の一大プロジェクトとして頑張った。んで、カードのイラストを25枚描いてもらった。これくらいの枚数でゲームバランスが良さそうだった。」
「……だけど、先程の『予想』によると25枚のカードすべてを使った【合成テーブル】は作れない(25は2の累乗じゃ表せないからね)。25に近い数字で、表が作れるものは『予想』によると 16 か 32 になってしまう。」
「せっかく描いてもらったのに、9枚も消すのは悲しいし、ゲームバランスが心配。でも7枚追加して描いてもらうのは申し訳ないし、うちの費用が心配。」
「どうにか、25枚ちょうどを使って表を作りたいわけだ。」
「ここまでくれば、君に解いて欲しい問題も分かるだろう。25枚のカードで、合成のルールを守っている【合成テーブル】を作ることは可能か調査して欲しい。無理なら、その理由を見つけて欲しい！」
「心得た！私にお任せあれ！」
.
.
.
(さて、25枚のカードで出来た表を実際に作るか、それが不可能ということを証明するか。はたまたさっきの『予想』の方を証明してしまうか……。)
この会話に登場した【合成テーブル】についての『予想』を、取り出してみましょう。
『予想』
合成の規則を満たす【合成テーブル】に使われる素材カードの枚数は、2の負でない整数の巾になり、それ以外にはならない。
つまり、カードの枚数は小さい順に並べると、
1 , 2 , 4 , 8 , 16 , 32 , 64 , 128 , ……
となる。
カードの枚数が1枚または2枚の時にも表が作れる、と言っていましたが、実際に作ってみると下の図のようになります。
(カードの枚数が1枚の時には、『ごみ』(表では「 g 」)の一枚のみになります。)
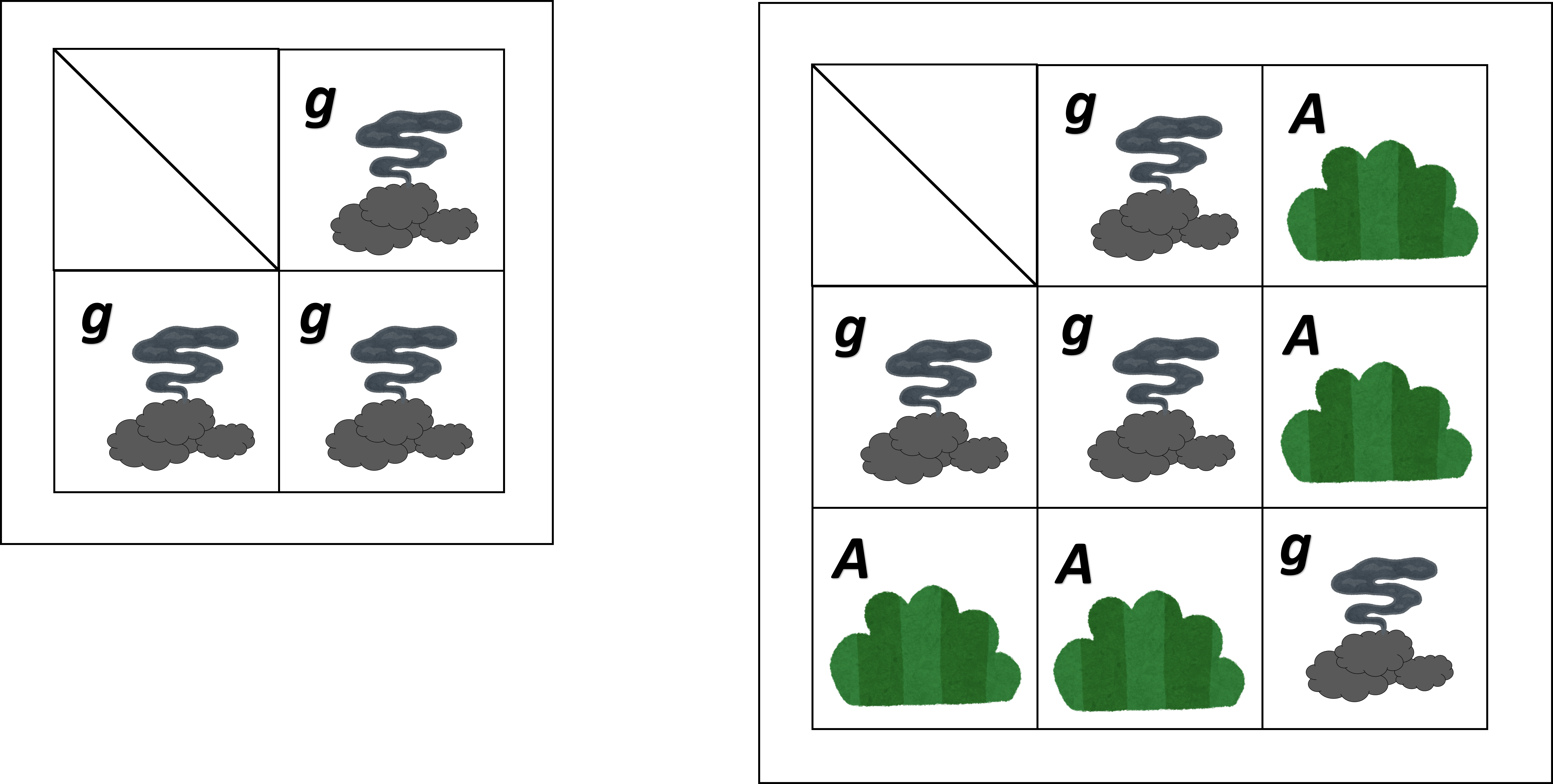カードの枚数が1枚、2枚の場合の合成表
そして先程、カードの枚数が3枚の時と4枚の時を見ていきました。
まとめると、合成の規則を満たす【合成テーブル】は、カードの枚数が1枚、2枚、4枚の時に実際に正しい表を作れますが、3枚の時には作れないということになります。
確かに、ここまでは予想通りのようですが、カードの枚数がもっと多い場合もこの予想が成り立つのでしょうか？
一応、今回あなたが最低限解かなければならない問題は、
登場する素材カードの枚数がちょうど25枚であるような、合成の規則を満たす【合成テーブル】は作成可能か、または不可能か。
となります。
しかし、この問題を直接解くか、はたまた【予想】の方を解いてしまうかはあなたの自由です。
会社の命運がかかっている『アトリエ』の、小さいけれど重要な問題を、すっぱり解決してみせてください！！
エピローグ
錬金術師ならだれでも、『賢者の石』の生成に憧れるもの。でもその前に、目の前の問題を解決しなくちゃ。
【『ニュートンのアトリエ リンカーシャンの錬金術師』ー プロローグ。 より】
ここまでの設定は全てフィクションです。ですが、登場した予想や問題は実際に私がまだ分かっていないものです。
もし今回の予想や問題に興味をもって、なにか分かったことなどがありましたら、まだまだ勉強の足りない私に教えては頂けないでしょうか。
また、この問題はもう解決済なのに、まだ何も分からないのか！という方がいらっしゃれば、そんな私に一つ助言でも頂けないでしょうか。
ここまで【設定編】・【問題編】と記事を読んでくださり、ありがとうございました。
この記事を高評価した人
この記事に送られたバッジ
投稿者
