荷電粒子を曲げたり絞ったり、加速器における磁場の役割〜サイクロトロン実験に寄せて〜

はじめに

こんにちは。荷電粒子を加速させたい、東京大学理学部物理学科３年のメラゾーマです。

東大理物の学生による有志団体Physics Lab. 2026のアドベントカレンダーとして、この記事を寄稿します。タグが付いているので是非他の記事もご覧ください！

Physlab. 2026には実験班があり、実験班の中でも各班に分かれて
実験計画を立てており、複数の実験をすることを予定しています。詳しくはこちらをご覧ください→。 Physics Lab. 2026 実験班紹介

私はその中でも、加速器の一種であるサイクロトロンを製作するというプロジェクトを進めています。ちなみに今回の実験の加速エネルギー目標は13.6 TeVです。。。嘘です。

今回の記事では、加速器について種類や加速の仕組みについてごく簡単に説明した後に、磁場に注目して加速器を見てみたいと思います。

加速器について全般的に紹介することも考えましたが、それだと概観すぎてこのサイトを見ている人たちは見づらいと思ったので、テーマを磁場に絞り、数式を用いた議論ができるようにしました。

加速器の概観

加速器とは

そもそも加速器は、荷電粒子を加速させる装置の総称です。何らかの方法で生成したイオンや電子を加速器に入射して、加速させて取り出します。取り出した後にどう使うかは分野によりますが、例えば何かにぶつけてみたり、加速粒子同士を衝突させてみたりします。ちなみに一番多く加速器が使われているのは医療現場で、こちらの記事を参考にしてみてください→ 医療現場で活躍する加速器

加速器の種類

加速器の種類は、電圧のかけ方とビーム軌道によって数種類に大別されています(図1)。このうち、大学受験で扱う加速器はコッククロフト・ウォルトン型加速器やサイクロトロンだと思います。私の興味によって偏っているかもしれませんが、よく見かける加速器は線形加速器とサイクロトロン, シンクロトロンです。

加速器の種類 ( KEK 加速器の原理と種類 より引用)

線形加速器(LINAC)

その名の通り直線型の加速器で、直線上の空間に高周波電圧をかけることで荷電粒子を加速します。がんの放射線治療に使われていたり、シンクロトロンの前段階の最初の加速で使われていたりします。

サイクロトロン

これは皆さん一度は運動方程式を解かされたことがあると思います。荷電粒子を磁場でぐるぐる回しながら、高周波電圧で加速させていきます。加速されるたび徐々に半径が大きくなっていきます。RI(放射性同位体)を作る目的で使われていることが多く、医療用RI生成や原子核実験に用いられています。図2は理研にあるリングサイクロトロンの写真です。一口にサイクロトロンと言っても電磁石の配置などによって色々な種類があります。

超伝導リングサイクロトロン「SRC」( 理研　仁科加速器科学研究センターより引用 )

シンクロトロン

KEKのsuperKEKBやCERNのLHCなど、素粒子実験のルミノシティフロンティアやエネルギーフロンティアにあるのはシンクロトロンです。決められた円周上を粒子が何周もぐるぐる回ることで加速されます。加速器の規模が大きく、superKEKBは全長約3 kmでLHCは全長約27 kmです。ここで紹介した２つはどちらも２つの粒子群を逆向きにまわして衝突点でぶつける衝突型の加速器ですが、標的を置いておいて加速させた粒子をぶつける標的型の加速器もあります。東海村にあるJPARCのシンクロトロンは標的型です。図3はsuperKEKBの全体図です。

KEK, CERN, JPARCは研究施設の名前で、superKEKBやLHCは加速器の名前です。Belle2とかATLASは実験名&検出器名です。

SuperKEKBプロジェクト全体図( KEK SuperKEKBプロジェクト全体図 より引用 ©KEK)

加速原理

ここで、一番大事な加速器の加速原理について説明します。ずばり、加速器は、荷電粒子のビームを電場で加速して、磁場で曲げたり絞ったりします。これは、高校物理のローレンツ力:$\boldsymbol{F} =q(\boldsymbol{E} + \boldsymbol{v ×B})$を考えてあげればよいです。

つまり、どれくらい加速するのかや、どのように加速させたいかを考えるときには電場がどのように分布しているかをみて、それ以外の加速しないところにおいてビームの軌道がどのようになっているかを見るには磁場の分布を見ます。

今回は磁場に関して考えてみるので、主にビーム内の粒子の軌道がどのようになるかを考えます。サイクロトロンやシンクロトロンは円形軌道を描くので、磁場で曲げていることがわかりますし、勝手にビームが広がっていっては困りますので、何かしら磁場で収束作用を働かせているはずです。

サイクロトロンと磁場

基本的な運動方程式

非相対論で考えます。z方向に大きさ$B$の磁場がかかっており、電荷$q$,質量$m$,速さ$v$の粒子が半径$R$で円運動しているときを考えて(下図)、運動方程式は

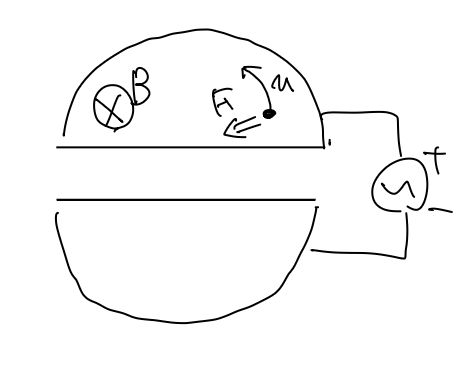サイクロトロン中の荷電粒子

$$ m\frac{v^2}{R}=qvB $$
で与えられます。この時、円運動の角振動数$\omega$と半径$R$は

$$ w = \frac{qB}{m} $$
$$ R=\frac{p}{qB}$$
で与えられます。$p$は運動量です。$\w$はサイクロトロン振動数と呼ばれます。ポイントは角振動数は速さや半径によらないこと、半径は運動量と磁場の大きさで決まることです。

なので、加速したい粒子の種類を決めて、磁場の大きさを決めれば、それに応じた周波数の電圧をかけると円運動している粒子を加速できるわけです。

弱収束の原理

理想的には先程の式のとおり、ぐるぐると円運動をしながら電圧で加速されるたびに半径を大きくしていくのですが、実際は何らかの要因で軌道が乱されて理想的な軌道(=参照軌道)から上や横にずれるでしょう。このとき、きちんと復元力が働いて元の軌道に戻ってほしいですよね。さて、さらに現実をみると、電磁石の磁場は一様ではなく、端に行くほど磁場が弱まって膨らんだ形になるはずです(下図)。

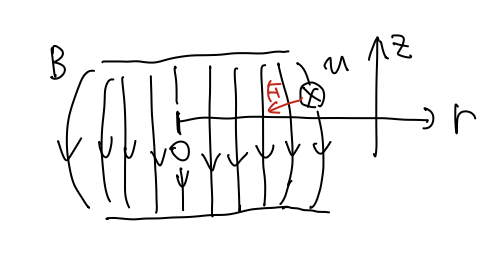端にいくほど弱まる磁場

実は、この磁場の形が参照軌道に戻すような復元力を粒子に及ぼすのです。これは弱収束の原理と呼ばれています。

まず、z方向(上方向)にズレたときのことを考えます。また、正しく図が描ければどちらでも言いのですが、今後電荷は$q>0$とします。円筒座標系を取って、同径方向の磁場成分を$B_r(z,r)$とします。今は軸対称な磁場分布を考えているので角度方向には依存しません。また、$B_r(z=0,r)=0$とします。この時、z方向に少しズレたときの磁場は

$$ B(z,r)\simeq \frac{\partial B_r}{\partial z}(z=0,r)z$$

と表されます。
さらにMaxwell 方程式のうち$\partial \boldsymbol{E}/\partial t$と電流成分$\boldsymbol{j}$を無視して、

$$\nabla \cross \boldsymbol{B} = 0$$

を用いて、

$$ \frac{\par B_r}{\par z} = \frac{\par B_z}{\par r}$$

とできます。また、角度方向の速度成分は

$$ v_\theta = r\omega$$

です。以上より、z方向にかかる力は

$$ F_z = -q v_\theta B_r\simeq -q v_\theta \frac{\par B_r}{\par z}z = -m\w^2 nz\ \ \ ・・・(1)$$

ただし、

$$ n(r)\coloneqq -\frac{r}{B_z}\frac{\par B_z}{\par r}|_{z=0} > 0$$

である。$n>0$のときは(1)が調和振動子の運動方程式になるので
、復元力が働く。よって、z軸にズレたときに復元力が働く条件は$n>0$であるし、この条件は外側に行くほど磁場が弱まると言っているので、一般的な(=一様磁場をかけようと思った有限面積の)電磁石なら満たされます。また、このときの角振動数は$\w_z = \sqrt{n}\w$となります。サイクロトロン振動数に対するz方向の振動数$\w_z$の比$\nu_z \coloneqq \w_z / \w = \sqrt{n}$は垂直方向のベータトロン振動数と呼ばれています。

符号がややこしすぎます。一般的に端になるほど弱まる磁場は、$B_z$が正のときは$\par B_z / \par r$は負に、$B_z$が負のときは$\par B_z / \par r$は正になります。よって$B_z$の方向によらず$n$は正です。

次に、同径(r)方向に少しズレた時を考えます。ここでも電荷は$q>0$です。元々$r=R$にいたのに少しズレて$r = R + x$になったとします。このときの力の同径方向成分$F_r$は

$$ F_r(r = R + x) = m\frac{v_\theta^2}{r} + qv_\theta B_z(r)$$

$B_z$は負です

ここで$x$は微少量なので展開します。すると、

$$ F_r(r = R + x) \simeq m\frac{v_\theta^2}{R}(1-\frac{x}{R}) + qv_\theta \{B(R) + \frac{\par B_z}{\par r}(z=0,R)x\}$$

$$ =-m\frac{v_\theta^2}{R^2}x+ qv_\theta\frac{\par B_z}{\par r}x$$

$$ =-m\w ^2 x -m\w^2\frac{R}{B_z}\frac{\par B_z}{\par r}x$$

$$ =-m\w^2(1-n)x$$

ただし、$r=R$のときは力は釣りあうので、 $m\frac{v_\theta^2}{R} + qv_\theta B_z(R) =0$ です。また、サイクロトロン振動について符号を考慮して$\w =-\frac{qB_z}{m}>0$ です。
以上より、z方向のズレの時と同様に復元力が働くための条件は、$1-n>0$です。このときの振動数は$\w_x = \w\sqrt{1-n}$ですし、z方向のズレを考えたときと同様に、水平方向のベータトロン振動数を$\nu_x = \w_z / \w=\sqrt{1-n}$と定義できます。

以上z方向と同径方向のズレに対して、復元力が働く条件を合わせると、

$$ 0< n<1$$

となります。図示すると下図のようになり、外側に行くほどこの条件は成立しなくなります。

同径方向の磁場分布と$n$の大きさ

問題点

この弱収束の原理は問題点があります。結局一様でない磁場を考えてしまったので、位相がずれてきてしまいます。また、$0< n<1$という制限がどうしてもあり不便です。そこで、別の収束原理を用いて加速させたくなります。AVFサイクロトロンやリングサイクロトロンと呼ばれるサイクロトロンは、弱収束の原理とは違う方法で収束作用を働かせるタイプのサイクロトロンです。

AVFサイクロトロンもリングサイクロトロンも理研(和光市)にあります。学生実験で理研にいけるので楽しみです。自分たちが製作しているサイクロトロンは弱収束を用いるものです。

シンクロトロンと磁場

はじめに電場について少し(位相安定性の原理)

この記事では磁場の役割について議論したいので詳細は省きますが、シンクロトロンのビームの運動を議論するうえで、位相安定性の原理というものが非常に重要な役割を果たします。これは高周波電場で粒子ビームを加速するときに出てくる議論で、このことで粒子はバンチ(束)になって動くことが言えます。詳しくは私も勉強中ですので、気になった人は調べてみてください。

曲線座標系

シンクロトロンについても、先程のサイクロトロンの弱収束の原理と同様に、参照軌道(=理想的な軌道)からズレたビームの運動を議論したいです。そこで、新しい座標系を導入します。まず、参照軌道上のある点を基準点とします。別の参照軌道上の点($\bm{r_0}$とします)を考え、基準点からその点までの参照軌道上の長さを$s$とします。まず、進行方向の単位ベクトルをとり、その向きの軸をs軸とします。また、ビーム軌道の平面内に水平で、かつ、s軸と直行する軸をとり、それをx軸とします。また、ビーム軌道の平面に垂直な軸をとり、それをy軸とします(サイクロトロンで議論したときはz軸と言っていたものです)。このようにすると、必ず直交する三軸がとれます(下図)。

曲線座標

参照軌道に曲率があるときは、円に対して外側(同径方向)を向くようにx軸を取ります。y軸はは$\hat{y} = \hat{s}\cross\hat{x}$とととればよいです。真っ直ぐ進むときはどうなんだと思いますが、シンクロトロンのように参照軌道が2次元に収まる限り軌道の外側を向くのがx軸のように考えれば一意に定まると思います。

磁場中の荷電粒子の運動

さて、ここからは一般的に荷電粒子の運動について、上で導入した座標系を用いて議論していきます。まず、ここでの目標は、x軸やy軸方向のズレ$(x,y)$についての、変数をsとするような運動方程式を立てることです。

以降では、ダッシュ($'$)は時間微分ではなくs微分のことを指します。気をつけてください。

気持ち悪い人向けに。今回は外場は磁場だけを考えているので、参照軌道上の粒子の速さは理想的には一定です。速さを$v$とでも置けば、$s=vt$としてすべて時間微分に置き換えればいいと思います。しかし、今回考えたいのは軌道上をビームが走るときに、何かの影響でビームがズレたときの動きを見たいので、やはり変数は参照軌道の曲線のパラメータであるsに取るほうが自然です。

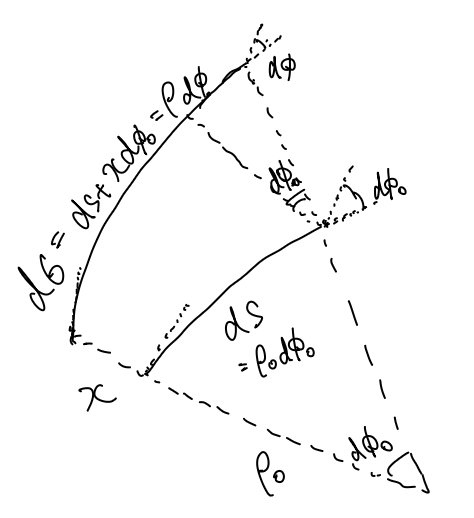運動方程式の導出
ここで、参照軌道からx軸方向に$x$だけズレた軌道を$ds$だけ動かしたときのことを考えます(上図)。参照軌道の曲率を$\kappa_{x0}$として、曲率半径を$\rho_{x0}=1/\kappa_{x0}$とします。まずは参照軌道について考えて、微小な偏向角$d\phi_0$は

$$ d\phi_{0}=ds/\rho_{x0} = \kappa_{x0}ds$$

で与えられます。これと同じように、参照軌道長から$x$だけずれた粒子の偏向角$d\phi$も、その粒子の曲率と曲率半径を$\k_x, \ \rho_x$として

$$ d\phi=d\sigma/\rho_{x} = \kappa_{x}d\sigma$$

で与えられます。ただし、$\k_{x0}$は参照軌道によって決まるものですが、$\k_{x}$は粒子の受ける力や運動量によって決まるものです。すなわち、

$$ \k_x = \frac{qB_y}{p}$$

で与えられます。ただし、$q$は電荷、$p$は粒子の運動量で、$B_y$はy軸方向の磁場の成分です。外積の関係から、y軸方向の曲率を考えるときは負符号がついて、

$$ \k_y = -\frac{qB_x}{p}$$

素粒子実験でよくやる、「磁場の大きさと飛跡の曲率がわかれば粒子の運動量がわかる」に使う関係式です。

また、ズレ$x$は十分小さいとして

$$ d\sigma = ds + xd\phi_0=(1 + \k_{x0}x)ds$$

が成立しますので、

$$ d\phi= \kappa_{x}d\sigma=\k_x(1 + \k_{x0}x)ds$$

また、$ds$進んだときの$x$の増加分$dx$は、偏向角の差で表せるので、

$$ dx = (\phi_0 -\phi)ds$$
$$ \therefore x' = (\phi_0 -\phi)$$

$x'$と偏向角の関係

$x'$の導出では$\phi,\phi_0$を有限の大きさのものと見ています。

よって、

$$ dx' = d(\phi_0 -\phi) = \{\k_{x0}-\k_x(1 + \k_{x0}x)\}ds$$

$$ \therefore x'' = \k_{x0}-\k_x(1 + \k_{x0}x)$$

これが、得たかった運動方程式になります。粒子に働く力の情報は$\k_x$が担っています。

上で行ったことは一般的な導出なので、y軸にも同じように適用できます。参照軌道は平面であるのが普通で、そのときは$\k_{y0} = 0$($\rho_{y0}=\infty$)であるので、

$$ y'' = -\k_y$$

となります。以上２つの運動方程式を元にして偏向電磁石と四極電磁石の中の荷電粒子の運動を議論します。

偏向電磁石の運動方程式(運動量の大きさ一定のとき)

以下しばらくは、参照軌道上の粒子に対して運動量の大きさが等しい時を考え、$p=p_0$とします。

手始めに、偏向電磁石における運動方程式を考えます。偏向電磁石は、磁場によってビーム方向を曲げるためにあります。シンクロトロンが円形になっているのは、偏向電磁石で曲げているからですね。

偏向電磁石の一例( KEK,SuperKEKBの陽電子リング用新型偏向電磁石の設置試験より引用 ©KEK)

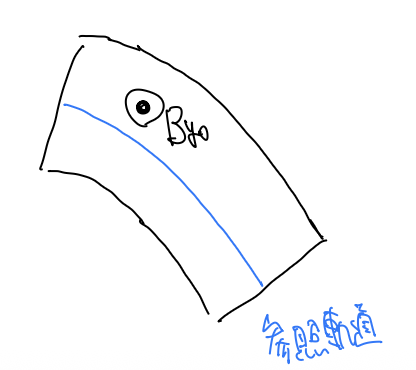理想的な偏向電磁石

理想的な偏向磁石を考えて、磁場は一様で$(B_x,B_y)=(0,B_{y0})$とします。また、参照軌道はx方向の曲率半径が$\rho_{x0}=\frac{p_0}{qB_{y0}}$の円軌道に取ります。このときは$\k_{x}=\k_{x0},\k_y=0$なので、先程求めた式に代入してあげると、

$$ x'' = -\k_{x0}^2x, \ \ y'' =0$$

が得られます。このときはサイクロトロンで議論した理想的な一様磁場の運動方程式と等価です。弱収束の原理の時と同じように、端にかけて弱くなるような磁場勾配を与えますと、この変化はパラメータ$n>0$で表されたことを思い出して、弱収束の原理と同様に

$$ x'' = -(1-n)\k_{x0}^2x$$
$$ y'' = -n\k_{x0}^2y$$

となります。

弱収束の原理のときは、時間微分に対応して角周波数$\w$が出てきましたが、今回は$s$微分に対応して曲率$\k_{x0}$が出てきます。

四重極電磁石の運動方程式(運動量の大きさ一定のとき)

次に四重極電磁石について考えます。四重極電磁石は、xy方向に広がってしまったビームを絞るためにあります。後でも詳しく扱いますが、レンズのような役割を果たします。

四重極電磁石( マグネットの種類,KEK より引用, ©2025 KEK)

ここでは、参照軌道は直線なので、参照軌道の曲率は$\k_{x0}=\k_{y0}=0$です。この時、運動方程式は、

$$ x'' = -\k_x\ \ y'' = -\k_y$$

となります。
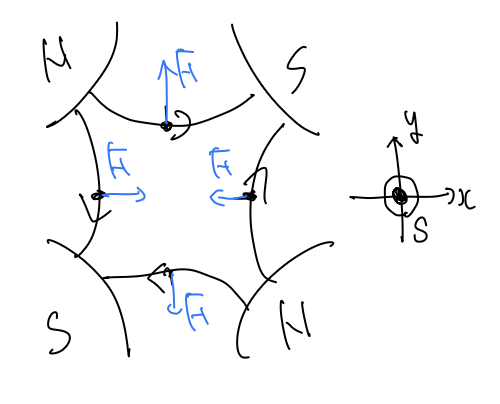理想的な四重極磁石

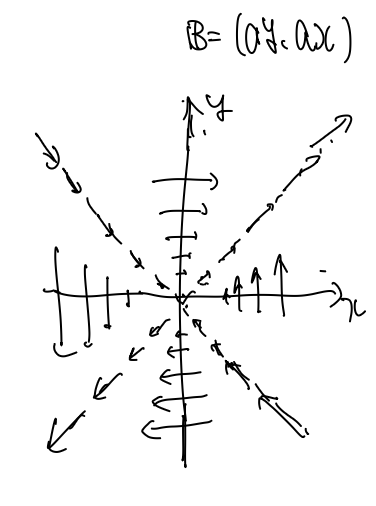四重極磁石の理想的な磁場分布
ここで、磁場を上図を参考にして

$$ (B_x,B_y) = (ay,\ ax)$$とします。これは理想的な四極磁場(磁場勾配)で、

$$ a = \frac{\par B_y}{\par x} = \frac{\par B_x}{\par y} \ \ @(x,y)=(0,0)$$

です($\nabla \cross \boldsymbol{B} = 0$)。

磁場が求まれば具体的に曲率を計算することができて、

$$ \k_x = \frac{qax}{p_0},\ \ \k_y = -\frac{qay}{p_0}$$

これを運動方程式に代入してあげて、$K\coloneqq qa/p_0$として、

$$ x'' = -\frac{qax}{p_0} = -Kx,\ \ y'' = \frac{qay}{p_0}=Ky$$

これは例えば図のときは$a>0$であるので、x軸方向には収束してy軸方向には発散することになります(F-Typeと言うそうです)。一方N極とS極を逆にして$a<0$にするとy軸方向に収束してx軸方向に発散します(D-Typeというようです)。このように、四重極磁石はレンズのような役割があると言いましたが、普通の光学のレンズと違って両方の方向に対して同時に収束させることができません。なのでビームラインではF-TypeとD-Typeが交互に設置されていて、「x軸に絞ってy軸にしぼって、、、」を繰り返しています。

転送行列

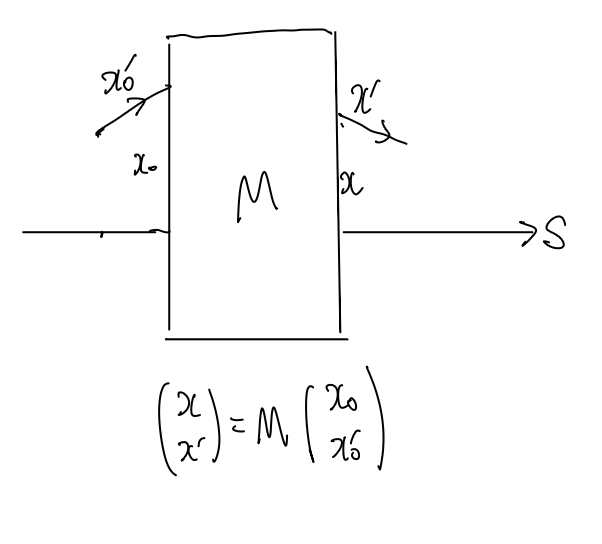
四重極磁石はビームを絞るレンズのような役割があると言いました。ので、幾何光学の類推と同じことを考えます。つまり、近軸近似をします(します、というかずっと本質的には近軸近似で粒子を追っています)。つまり、参照軌道の近傍のみで粒子の軌跡を追う、ということです。このとき、例えばxs平面における粒子の運動を特徴付けるパラメータは、$x,x'$の２つです(下図)。

近軸近似

いまは$x'\simeq \tan x'$ですので、$(x,x')$を「ズレとその傾き」と見てもらっても「ズレと角度」と見てもらっても良いです。

なので、$s$が変化したときのビームの変化(=$x,x'$の変化)を行列で表現できます(上図)。この行列のことを、幾何光学では光線行列やABCD行列といいますが、ビーム力学の文脈では転送行列と呼ばれています。

幾何光学でも転送行列といいますか？わからないので詳しい人教えて下さい。

絵を描いて考えればよいですが(図)例えば何もない自由空間での転送行列は、

$$ M_O(L) = \begin{pmatrix}   1 & L \\   0 & 1\end{pmatrix}$$

となります(下図)。

自由空間の転送行列

四重極磁石の転送行列

さて、先程求めた四重極磁石の運動方程式から、転送行列を求めてみます。今は$a>0$、つまり$K>0$を考えることにして、x軸方向にビームを絞ろうと思います(F-Type)。改めて運動方程式を書くと、

$$ x'' = -Kx$$

です。一般解は調和振動子なので、$s=0$で$(x,x') = (x_0,x_0')$となるように決めると、

$$ x = \frac{x_0'}{\sqrt{K}}\sin\sqrt{K}s + x_0\cos\sqrt{K}s$$

$$ x' = x_0'\cos\sqrt{K}s - x_0\sqrt{K}\sin\sqrt{K}s$$

となるので、転送行列は

$$ \begin{pmatrix}   \cos\sqrt{K}s & \frac{１}{\sqrt{K}}\sin\sqrt{K}s \\   - \sqrt{K}\sin\sqrt{K}s & \cos\sqrt{K}s\end{pmatrix}$$

となります。逆に$K<0$でx軸方向に発散してしまうとき(D-Type)の転送行列は同様にして($\cosh' =\sinh$に注意して)、

$$ \begin{pmatrix}   \cosh\sqrt{|K|}s & \frac{１}{\sqrt{|K|}}\sinh\sqrt{|K|}s \\    \sqrt{|K|}\sinh\sqrt{|K|}s & \cosh\sqrt{|K|}s\end{pmatrix}$$

このままだとレンズ感がないので、$s→0$の極限を取ります。ただし、$k=|Ks|=const.$とします(肉薄近似と言うそうです)。

厚みはゼロにするけど、曲げる能力(屈折力)はそのままにする近似。

このとき、

$$ M_F(k) =\begin{pmatrix}   1 & 0 \\   -k & 1\end{pmatrix} \ \ (\text{F-Type})$$
$$ M_D(k) =\begin{pmatrix}   1 & 0 \\   k & 1\end{pmatrix} \ \ (\text{D-Type})$$

となります。これは各々が焦点距離が$1/k$の凸レンズと凹レンズを表しており、それぞれ収束・発散するということが直感的にもわかると思います。y軸のときはF-TypeとD-Typeが逆になるだけで良いですね。

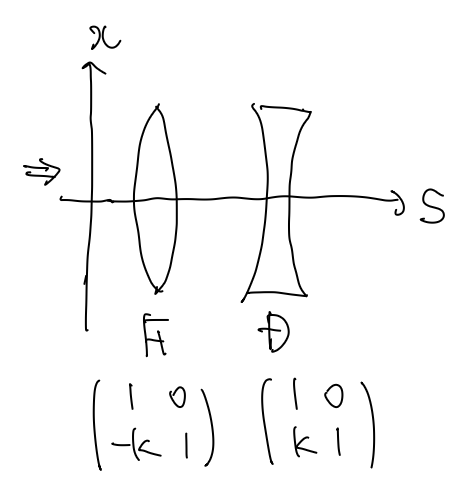肉薄近似したときのF-TypeとD-Type(x軸方向)

四極電磁石の組み合わせ

以上のように転送行列が求まったら、転送行列を掛算することでビームの運動を追跡することができるようになります。前述した通り、四重極電磁石は一方の軸で収束させているときはもう一方の軸は発散させているので、必ずF-TypeとD-Typeを組み合わせています。さらに、電磁石間は自由空間($O$と呼びます)を動くので、今回は$FODO$で1セットとなるようなものを考えます(下図)。自由空間の距離を$L$として、実際に$FODO$のx軸方向の転送行列を計算してみます。条件が簡単になるように、FとDの焦点距離が違うものを考えて、

$$ M_{FODO} = M_O(L)M_D(k)M_O(L)M_F(k/2)$$

$$ =\begin{pmatrix}   1 & L \\   0 & 1\end{pmatrix}\begin{pmatrix}   1 & 0 \\   k & 1\end{pmatrix}\begin{pmatrix}   1 & L \\   0 & 1\end{pmatrix}\begin{pmatrix}   1 & 0 \\   -k/2 & 1\end{pmatrix}$$

$$ = \begin{pmatrix}   1-\frac{k^2L^2}{2} & 2L + kL^2 \\   \frac{k}{2} - \frac{k^2L}{2} &KL+1 \end{pmatrix}$$

FODOが続いていく様子. 実際は偏向や六重極電磁石や高周波電圧の加速空洞との組み合わせでビームラインができている.

一般的にFとDの焦点距離は異なるものを用いているようです。このとき収束力を$k_F,k_D$とおいて議論します。

ここで、ビームが収束するような条件を考えます。これはすなわち、適当な$(x,x')$がこの行列を通過したときに、各々の値が大きくなっていなければいいわけですから、転送行列$M_{FODOF}$の２つの固有値の絶対値がどちらも1以下になればよいです。２つの固有値を$\lambda_1, \lambda_2$として

$$ |\lambda_1|, |\lambda_2| \leq 1 $$

もう少しきちんというと、ビーム内をぐるぐる回るうちにこの$FODOF$を何回も($N$回)通過することを考えています。このときは$(x,x')$を適当に固有ベクトルの線形和で書くと、各々の固有ベクトルに$\lambda^N$がかかってくるので、これの収束性を言うには上の条件が出てきます。

また、各$M_F,M_D,M_O$の行列式は1なので、$\det M_{FODO}=1$です。よって$$ \lambda_1\lambda_2=1$$

$\det M =1$は$x,x'$の位相空間の体積が不変であることを言っており、Liouvileの定理に対応します。

以上の条件から

$$ |\lambda_1| = |\lambda_2| = 1$$

が言えて、上式と合わせて

$$ \lambda_1=e^{i\mu}, \lambda_2=e^{-i\mu}$$

となります。よって、

$$ \Tr M = 2\cos \mu$$

$\mu$は実数であることが必要なので、　$|\Tr M|\leq2$が安定条件になります。

例えば先程求めた$M_{FODOF}$の安定条件は、

$$ |\frac{-k^2L^2}{2} + kL + 2|\leq 2$$

なので、$$ f=1/k\geq L/2$$

が安定条件になります。今はx軸の安定条件を考えましたが、後はy軸方向にも考えないといけません。より一般に、x軸とy軸の収束力の違い(すなわち焦点距離の違い)を反映して、$k_F,k_D$として議論を進めることもできます。

偏向電磁石の転送行列

四重極電磁石と同じように、偏向電磁石についても転送行列を求めることができます。計算してみると、$\det M=1$を満たしています。計算してみてください。

運動量のズレ

今まで扱ってきた転送行列や運動方程式の解は、必ず運動量の大きさは一定として、参照軌道にいる理想的な粒子に合わせたものでした($p=p_0$)。しかし、実際は運動量もばらつきます。そのような運動量のずれも考えようと思うと、転送行列は3×3になりますよね。運動方程式に立ち返る(下式)と、曲率に運動量の情報が乗っているので、これを$p=p_0 + \delta$として$\delta$で展開していけば良さそうです。詳しく立ち入ることは今回はしません。

$$ \k_x = \frac{qB_y}{p}$$
$$ \k_y = -\frac{qB_x}{p}$$
$$ x'' = \k_{x0}-\k_x(1 + \k_{x0}x)$$ $$ y'' = -\k_y$$

六重極電磁石

また、上で述べたようにビームの運動量は有限の幅を持っているので、曲率は運動量に依存して異なってきます。また、四重極電磁石における収束力のパラメータ$k$は元を辿ればビームの曲率に依存します(辿ってみてください)。よって、四重極磁石による収束は、運動量によって異なってきます。この収束力の差を補正するものとして、六重極電磁石があります。光学系のアナロジーでこのような補正は色収差補正と呼ばれています。

六重極電磁石( マグネットの種類,KEK より引用, ©2025 KEK)

終わりに

いかがだったでしょうか。加速器のビームラインに馴染みましたでしょうか。今回触れたことは加速器物理の基礎中の基礎なところのみで、実際にはもっと様々なことを考えないといけません(なにより今回は磁場しか考えていないので加速できません。。。)

現場、例えばKEKやJPARCでは「加速器」を専門とするプロフェッショナルな方達がいて、そのような人々の技術の結晶として加速器があります。もしビームラインを見学する機会がありましたら、そのメカメカしさに驚嘆するだけでなく、その技術力や、その技術力を持つプロの方々に思いを馳せてみてください。自然と尊敬の念を抱くことでしょう。