半直積について2 半直積として実現されない群
前回 も半直積にならない群を見ましたが,今回はまず前回の具体例を少し一般化したものをみていきます.前回は単位元を$e$と表記しましたが,今回はアーベル群も出てくるので$0,1$を用います.引き続きRotman,An Introduction to the Theory of Groupsの主に7章のコピペ(和訳)が大きな割合を占めます.
一般四元数群$Q_n$($n\geq 3$)とは$2$つの元$a,b$で生成される位数$2^n$の群で$a^{2^{n-1}}=1$,$bab^{-1}=a^{-1}$,$b^2=a^{2^{n-2}}$を満たすもののことである.
このような群は存在すれば同型を除いて一意に定まります.なぜなら,群の位数の条件からそのような群の元を列挙することができ,$\{a,a^2,...,a^{2^{n-1}},ab,...,a^{2^{n-1}}b\}$となります.これらの積は与えられた関係式から計算できます.
実際に一般四元数群が存在することをみましょう.
$G\leq \text{GL}(2,\mathbb{C})$を
$A= \begin{eqnarray}
\left(
\begin{array}{cc}
\omega & 0 \\
0 & \bar{\omega}
\end{array}
\right)
\end{eqnarray} $, $B=\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}
\right)
\end{eqnarray} $で生成される群とする.ここで$\omega$は$1$の原始$2^{n-1}$乗根であり,$\bar{\omega}$はその共役である.これは$A=a$,$B=b$とすることで確認できるように,一般四元数群と同型である.実際,これらの元で生成される群は位数$2^{n}$であり,定義に現れる関係式を満たすことが計算によりわかる.
$Q_n$は位数$2$の元$z$をただ一つもち,中心は$Z(Q_n)= \langle z \rangle $.
$a,b$の位数はそれぞれ$2^{n-1}$,$4$.$ab=ba^{-1}$なので$x\in Q_n$は$0\leq s\leq 2^{n-1}-1$,$0\leq t\leq 3$を用いて$x=a^sb^t$とおける.$x$が位数$2$であるとすると$x^2=b^{2t}=1$なので$t=0,2$である.$b^2=a^{2^{n-2}}$だから$x=a^s$としてよい.$a^{2s}=1$から$s=2^{n-2}$となり$x=a^{2^{n-2}}$.次に$x\in Z(Q_n)$とする.$b$との可換性から$ba^sb^t=a^sb^{t+1}$,$a^{2s}=e$,よって$s=0,2^{n-2}$.$1,a^{n-2}$は明らかに$Z(Q_n)$の元なので$Z(Q_n)=\langle z\rangle$.$\Box$
ちなみに商について次が成り立ちます.
$Q_n/Z(Q_n)\cong D_{2^{n-2}}$.ただし$D_{2^{n-2}}$は$2^{n-2}$次の二面体群.
$[a]$,$[b]$は$[a]^{2^{n-2}}=1$,$[b^2]=1$,$[b][a][b]=[bab^{-1}]=[a]^{-1}$を満たす生成元なので,成り立つ.$\Box$
上の命題により次のことがわかります.
$Q_n$は非自明な群による半直積にならない.
$Q_n$の部分群の位数は$2$のべきだが,位数$2$の部分群は一つしかないため,コーシーの定理により,非自明な部分群の組で$N,H< Q_n$で$N\cap H=\{1\}$となるものが存在しない.$\Box$
もとの群がいつ正規部分群とそれによる商群の半直積で表せるかという当初の問題に戻ると,このようにどんな非自明な部分群にも含まれる共通の部分群が存在すれば,もとの群は半直積として表せないことがわかります.しかし,そのような群は$p-$群に限れば一般四元数群に限られることがわかるそうです.(気になる方は参考文献のリンクをご参照ください)
反対に,半直積で表すことができるための十分条件を得るために,状況を一般化します.
$K,Q$を群とするとき,$K$の$Q$による拡大とは群$G$であって,$K\cong K_1 \triangleleft G$,$G/K_1\cong Q$を満たすもののことをいう.
これは$1\to K\to G\to Q\to 1$が短完全列となることを意味します.つまり$K,Q$を与えた上で短完全列の真ん中を求めよう,ということです.しかし,これだけでは情報が不足するので半直積から他の構成要素を探してみましょう.
$G$を$Q$による$K$の半直積とすると,準同型
$\theta:Q\to \text{Aut}(K),x\mapsto \theta_x=\gamma_x|_K$が存在する.ただし,$\gamma_x$は$x$による共役を表す.
証明は省きます.準同型があるわけですね.
逆に次のことも成り立ちます.
$Q$,$K$を群とする.準同型$\theta:Q\to \text{Aut}(K)$に対し$G=K\rtimes _\theta Q$を集合としての直積$K\times Q$に積
$(a,x)(b,y)=(a\theta_x(b),xy) $を入れたものであるとする.
内部半直積から外部半直積を作ることができます.
$G$を$K$の$Q$による半直積とすると,$\theta:Q\to \text{Aut}(K)$で$G\cong K\rtimes_\theta Q$となるものが存在する.
証明は省きますが,$\theta(x)=\gamma_x|_K$とすればよいです.
もちろんこれらの半直積は$K$の$Q$による拡大となっています.さらに必要な概念を定義していきます.
$\pi:G\twoheadrightarrow Q$を全射準同型とする.$x\in Q$の持ち上げ(lifting)とは$l(x)\in G$であって$\pi(l(x))=x$を満たすものをいう.右(左)代表系は商への自然な射影に関する持ち上げである.特に$\ker\pi$の右代表系を単に代表系という.
以下では$G$が$K$の拡大である場合に$g\in G $,$k\in K$に対してそれらの積を表すのに加法的な記号を用い,$g+k-g$のように表します.共役が見やすいですね!
$G$を$K$の$Q$による拡大とする.$l:Q\to G$を代表系とする.$K$をアーベル群とすると,準同型$\theta:Q\to \text{Aut}(K)$,$\theta_x(a)=l(x)+a-l(x)$が存在する.$l_1:Q\to G$をもう一つの代表系とすると,任意の$a\in K$,$x\in Q$に対し
$l(x)+a-l(x)=l_1(x)+a-l_1(x)$が成り立つ.
$K\triangleleft G$だから$g\in G$に対し$\gamma_g|_K\in \text{Aut}(K)$.$\mu:G\to \text{Aut}(K)$,$g\mapsto \gamma_g|_K$は準同型で$K$はアーベル群だから$K\leq \ker \mu$.よって$\mu_\sharp :G/K\to \text{Aut}(K)$が定まり,これは代表系の取り方によらない.$\Box$
この定理でアーベル群の仮定を用いましたが,一般の場合も$\theta:Q\to \text{Aut}(K)/\text{Inn}(K)$とすれば成り立ちますが,先が複雑になるのでここでは通常通り,アーベル群であることを以降仮定します.
こうして拡大を扱う準備が終わります.
$K$をアーベル群,$Q$を群,$\theta:Q\to \text{Aut}(K)$を準同型とする.順序対$(Q,K,\theta)$をデータ(data)という.群$G$が$K$の$Q$による拡大であり,任意の代表系$l:Q\to G$,及び$x\in Q$,$a\in K$に対し
$xa:=\theta_x(a)=l(x)+a-l(x)$が成り立つとき,$G$はこのデータを実現するという.
直感的には$\theta$は$K$が$G$のどのような部分群かを述べていると考えることができます.例えば$K$が$G$の中心の部分群なら$\theta$は自明になります.
目標は与えられたデータ$(Q,K,\theta)$に対して,これを実現する群$G$を全て求めることになります.短完全列の真ん中を求める問題に$\theta$に関する条件がついたということですね.
定理$5$は$G$が$K\triangleleft G$,$Q=G/K$,$\theta$を実現することを述べる.
$\theta$を自明な準同型とすると,一般化四元数群は$(Z(Q_n),Q_n/Z(Q_n),\theta)$を実現するが,半直積にならない.
$\pi:G\to Q$を全射準同型,その核を$K$とする.$l:Q\to G$を$l(1)=0$を満たす代表系とすると,任意の$x,y\in Q$に対し,ある$f(x,y)\in K$が存在して
$l(x)+l(y)=f(x,y)+l(xy) $を満たす.このときこの$f:Q\times Q\to K$をfactor setまたはコサイクルという.
$l(x)+l(y)$と$l(xy)$は$K$が正規部分群であることから同じ剰余類の元なのでこのような$f$が存在します.
$f$は$l$が準同型からどれだけ離れているかを表します.$l$が準同型なら短完全列は分裂し,$G$は半直積となるので,結局$f$は$G$が半直積からどれくらい離れているかを表します.
コサイクルは次の条件を満たします.
$\pi:G\to Q$を全射準同型,$K$を$\pi$の核,$l:Q\to G$を$l(1)=0$を満たす代表系,$f:Q\times Q\to K$を対応するコサイクルとする.このとき次が成り立つ.
(i) 任意の$x,y\in Q$に対して$f(1,y)=0=f(x,1)$
(ii) (コサイクル恒等式) 任意の$x,y,z\in Q$に対して
$f(x,y)+f(xy,z)=xf(y,z)+f(x,yz)$.
ただし,$Q$の$K$への作用を$x\in Q$,$a\in K$に対し
$xa:=l(x)+a-l(x)$で表した.
(i) $l(1)+l(y)=0+l(y)$,$l(x)+l(1)=0+l(x)$なので$f(1,y)=0=f(x,1)$.
(ii) 積の結合則により
$(l(x)+l(y))+l(z)=f(x,y)+l(xy)+l(z)$
$=f(x,y)+f(xy,z)+l(xyz)$,
$l(x)+(l(y)+l(z))=l(x)+f(y,z)+l(yz)$
$=xf(y,z)+l(x)+l(yz)=xf(y,z)+f(x,yz)+l(xyz)$.$\Box$
この定理は$K$が可換な場合逆も成り立ちます.
与えられたデータ$(Q,K,\theta)$,関数$f:Q\times Q\to K$に対し,$f $がコサイクルであることと,任意の$x,y,z\in Q$に対しコサイクル恒等式
$f(x,y)+f(xy,z)=xf(y,z)+f(x,yz)$及び
$f(1,y)=0=f(x,1)$を満たすこととは同値である.より正確には,データを実現する拡大$G$と代表系$l:Q\to G$で$f$が対応するコサイクルとなるものが存在する.
証明は次回に回そうと思います.
特にデータ$(Q,K,\theta)$,コサイクル$f$を実現する拡大を$G_f$と書きます.
データ$ (Q,K,\theta)$に対応するコサイクル全体のなす集合を$Z^2(Q,K,\theta)$と表す.
$Z^2(Q,K,\theta)$にはコサイクルとなるための同値な条件からわかるように各点の積によってアーベル群の構造が入ります.
ところで,異なるコサイクルであっても実現される群が同型となることがあり,これらを同一視することを考えるのは自然な流れです.
$G$を$(Q,K,\theta)$を実現する拡大,$l,l'$を$l(1)=0=l'(1)$を満たす代表系,それらに対応するコサイクルをそれぞれ$f,f'$とする.このとき関数$h:Q\to K$であって$h(1)=0$を満たし任意の$x,y\in Q$に対し
$ f'(x,y)-f(x,y)=xh(y)-h(xy)+h(x)$を満たすものが存在する.
これで割るべき集合がわかりました.
与えられたデータ$(Q,K,\theta)$のコバウンダリとは,関数$g:Q\times Q\to K$であって,ある$h:Q\to K$で$h(1)=0$,$g(x,y)=xh(y)-h(xy)+h(x)$,$(x,y\in Q)$を満たすものが存在するものをいう.
コバウンダリ全体の集合を$B^2(Q,K,\theta)$と書く.
$B^2(Q,K,\theta)$は明らかに$Z^2(Q,K,\theta)$の部分群です.
与えられたデータ$(Q,K,\theta)$に対し
$H^2(Q,K,\theta)=Z^2(Q,K,\theta)/B^2(Q,K,\theta)$
はデータの2次のコホモロジー群という.
すると次の定理が成り立ちます.
データ$(Q,K,\theta)$を実現する2つの拡大$G,G'$が同型であることと次の図式を可換にする同型$\gamma$が存在することは同値である.ここで,2つの行は完全である.
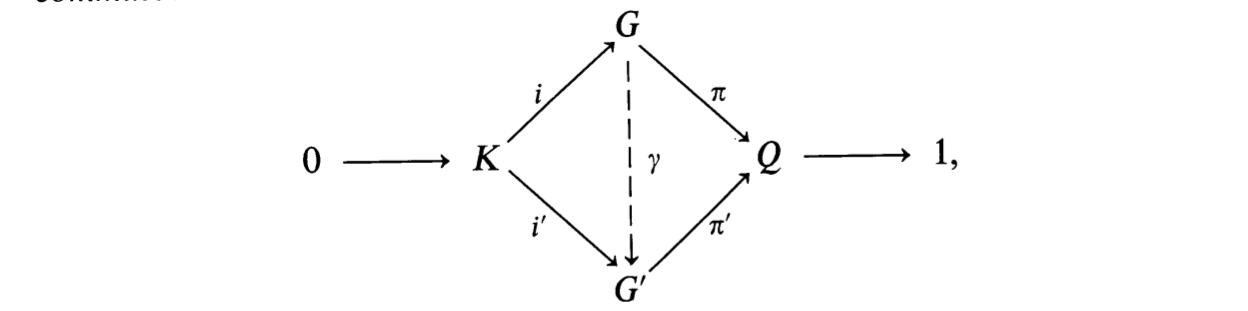
以上をまとめると次の定理が成り立ちます.
$H^2(Q,K,\theta)$からデータ$(Q,K,\theta)$を実現する拡大の同型類への全単射で,$0$を半直積に対応させるものが存在する.
よって最初の正規部分群と商群の積が戻るかという問題ですが,次の十分条件を得ました.
$H^2(Q,K,\theta)=0$なら成り立つ!.
元々はゼミで出た質問を,勝手にこうした形で記事にしてしまいましたがお許しください.
参考文献:
mathlog, Why is the generalized quaternion group 𝑄𝑛 not a semidirect product?
J.J.Rotman,An Introduction to the Theory of Groups,GTM,1994
