積分問題集の解説(初級)

517

はじめに

この問題を公開してから期限の2週間に到達したので解法を公開していきます.
解法は初級〜超級の4つに分けて公開しようと思っています.
また良い解法があれば解答してくださった方々の解法も使用させていただきます.

解説

$\begin{array}{r} \int_{- π / 2}^{π / 2} \frac{\cos^{2} x}{1 + e^{\sin x}} d x = \frac{π}{4} \end{array}$

これは高校範囲の問題ですね.
指数関数,三角関数が入り混じっていますが今回は定積分でしかも範囲が良いので恐れることなかれです.
今回使用していく解決策はキングプロパティ(以下略称:kp)です.
$[a, b]$ の積分について $b + a - x = t$
と置換し,置換する前の積分と後の積分を足して2で割るというものです.

$\begin{array}{r} I := \int_{- π / 2}^{π / 2} \frac{\cos^{2} x}{1 + e^{\sin x}} d x \end{array}$
$\begin{array}{rcl} = & \int_{π / 2}^{- π / 2} \frac{\cos^{2} (- x)}{1 + e^{\sin (- x)}} (- d x) (x \to - x) \\ = & \int_{- π / 2}^{π / 2} \frac{\cos^{2} x e^{\sin x}}{1 + e^{\sin x}} d x = I^{'} \end{array}$
$\begin{array}{rcl} I & = & \frac{I + I^{'}}{2} (∵ I^{'} = I) \\ = & \frac{1}{2} \int_{- π / 2}^{π / 2} \cos^{2} x d x \end{array}$
あとは計算するだけですが僕的には2つの解法があるので紹介したい方のみ解説します.
1つ目は半角を用いて2乗を解消する方法
2つ目はkpを用いて一瞬で終わらせる方法です.
後者を紹介します.
$\begin{array}{rcl} A : & = & \int_{- π / 2}^{π / 2} \cos^{2} x d x \\ = & 2 \int_{0}^{π / 2} \cos^{2} x d x \\ = & 2 \int_{0}^{π / 2} \sin^{2} x d x (\frac{π}{2} - x \to x) \end{array}$
$\begin{array}{rcl} 2 A & = & 2 \int_{0}^{π / 2} \cos^{2} x + \sin^{2} x d x \\ = & π \end{array}$
$\begin{array}{r} ∴ I = \frac{A}{2} = \frac{π}{4} \end{array}$
こんな感じで示せました.

kpは大学受験でもよく出されるので知っておいて損は無いと思います.

$\begin{array}{r} \int_{0}^{π} \arccos \cos^{2 n + 1} x d x = \frac{π^{2}}{2} \end{array}$

まずarccosとは何かですね.
調べてみるとcosの逆関数であることがわかります.
$\begin{array}{r} \arccos x := \int_{x}^{1} \frac{d t}{\sqrt{1 - t^{2}}} \end{array}$
としましょう.
この積分を弄くれば
$\arccos x = \frac{π}{2} - \arcsin x$
となることがすぐにわかります.
(積分区間を[0,1]と[0,x]に分けて積分)
またarcsinには次の性質があります.
$\arcsin (- x) = - \arcsin x$
xにsin xを入れてみればわかりますね.
ではこれらの性質を用いて証明していきましょう.

$\begin{array}{r} \int_{0}^{π} \arccos \cos^{2 n + 1} x d x \end{array}$
$\begin{array}{rcl} = & \int_{0}^{π} \frac{π}{2} - \arcsin \cos^{2 n + 1} x d x \\ = & \frac{π^{2}}{2} - \int_{0}^{π} \arcsin {(- \cos x)}^{2 n + 1} d x (π - x \to x) \\ = & \frac{π^{2}}{2} \end{array}$
途中A=-Aなる実数はA=0となることからarcsinの積分が0になる事を使いました.

$\begin{array}{r} \int \prod_{k = 1}^{n} a_{k} (x) d x = a_{n} (x) + C \\ a_{n + 1} (x) = e^{a_{n} (x)}, a_{1} (x) = e^{x} \end{array}$

数列じゃない書き方をすれば
$\begin{array}{r} \int e^{x} e^{e^{x}} e^{e^{e^{x}}} d x = e^{e^{e^{x}}} + C \end{array}$
となり,見た目が面白いですよね.
今回は数学的帰納法を用いて証明していきます.
しかも今回は不定積分なので右辺微分して被積分関数と一致することを確かめれば十分です.

$\int e^{x} d x = e^{x} + C$ より
n=1で成り立つ
n=mで成り立つと仮定し
n=m+1で成り立っていることを示す.
$\begin{array}{rcl} \frac{d}{d x} a_{m + 1} (x) & = & \frac{d}{d x} e^{a_{m} (x)} \\ = & \frac{d}{d x} a_{m} (x) \cdot \frac{d}{d a_{m} (x)} e^{a_{m} (x)} \\ = & e^{a_{m} (x)} \prod_{k = 1}^{m} a_{k} (x) \\ = & \prod_{k = 1}^{m + 1} a_{k} (x) \end{array}$

こういった数学的帰納法を考えるのは数列を含む積分では使えることがあります.

$\begin{array}{r} \int_{0}^{π} \frac{x}{a + \cos^{2} x} d x = \frac{π^{2}}{2 \sqrt{a (1 + a)}} (a > 0) \end{array}$

題意をIと置く
$\begin{array}{rcl} I & = & \int_{0}^{π} \frac{π - x}{a + \cos^{2} x} d x (x \to π - x) \\ = & \int_{0}^{π} \frac{π}{a + \cos^{2} x} d x - I \end{array}$
$\begin{array}{rcl} ∴ I & = & \frac{π}{2} \int_{0}^{π} \frac{d x}{a + \cos^{2} x} \\ = & π \int_{0}^{π / 2} \frac{d x}{a + \cos^{2} x} \\ = & π \int_{0}^{\infty} \frac{d t}{1 + a + a t^{2}} (\tan x \to t) \\ = & π \int_{0}^{π / 2} \frac{d t}{\sqrt{a (1 + a)}} (\sqrt{a} t \to \sqrt{1 + a} \tan t) \\ = & \frac{π^{2}}{2 \sqrt{a (1 + a)}} \end{array}$

この問題はあまり話したいと思うことがないですね…
高校範囲の問題ではかなり難しい部類なのでしょうか.

$\begin{array}{r} \int_{0}^{\infty} \frac{d x}{(1 + x^{2}) (9 + x^{2}) (25 + x^{2})} = \frac{π}{640} \end{array}$

これは想定解は部分分数分解です.
やることは同じなので解答して頂いた方からの写真を引用させてもらいました.(もちろん許可付き)

(解答してくださった方: hiro さん)
あとは留数定理による解法も考えられますね.
そしてこの積分で話したいことは次のような一般化があるということです.

$\begin{array}{r} \int_{0}^{\infty} \prod_{k = 1}^{n} \frac{1}{(2 k + 1)^{2} + x^{2}} d x = \frac{π}{2^{2 n + 1} (2 n + 1) n!^{2}} \end{array}$

尚,これは keitadayo さんの次の記事で出されているものです.

積分と級数の問題

keitadayoさんとこの積分について話した結果,僕とkeitadayoさんで2つの解法が出ました.
その僕の解法は今後上級の解説にて出そうと思っています.

$\begin{array}{r} \int_{0}^{2 π} \frac{d x}{\cosh a + \cos x} = \frac{2 π}{\sinh a} (a > 0) \end{array}$

これは区間を分けてワイエルシュトラス置換をすれば高校範囲で解けますが今回は別の方法で解きます.
今回使うのは留数定理による解法です.
自分語りになりますが留数定理を使い始めた頃,今回の問題のようなものの解説でこんな簡単に解けるのか！と驚かされました.
その解説というのが次のYoutubeの動画です.

動画のリンク

わかりやすく解説されているので留数定理初心者でもこの動画なら理解できると思います.
今回の問題を解く方法はこの動画の方法と同じです.

$\begin{array}{rcl} \int_{0}^{2 π} \frac{d x}{\cosh a + \cos x} & = & \int_{0}^{2 π} \frac{2 d x}{2 \cosh a + e^{i x} + e^{- i x}} \\ = & \int_{0}^{2 π} \frac{2 e^{i x} d x}{e^{2 i x} + 2 \cosh a e^{i x} + 1} \\ = & \frac{2}{i} \oint_{| z | = 1} \frac{d z}{z^{2} + 2 \cosh a z + 1} (e^{i x} \to z) \\ = & \frac{2}{i} \oint_{| z | = 1} \frac{d z}{(z + e^{a}) (z + e^{- a})} \\ = & 4 π {Res}_{z = - e^{- a}} \frac{1}{(z + e^{a}) (z + e^{- a})} (∵ a > 0) \\ = & 4 π lim_{z \to - e^{- a}} \frac{1}{z + e^{a}} \\ = & \frac{2 π}{\sinh a} \end{array}$

こんなすんなりと解けてしまいました！
皆せーので言いましょう…

留数定理気持ち良すぎだろーー！！！

元ネタ

$\begin{array}{r} \int_{0}^{1} \frac{x}{x^{5} + x^{4} + x^{3} + x^{2} + x + 1} d x = \frac{π}{12 \sqrt{3}} + \frac{1}{4} \ln 3 - \frac{1}{3} \ln 2 \end{array}$

これは高校範囲の変形でも解けるらしいです.(僕は部分分数分解で解けるだろうと思ってましたが実際は計算していませんでした)
その変形というのをまたまたhiroさんから引用させてもらいます

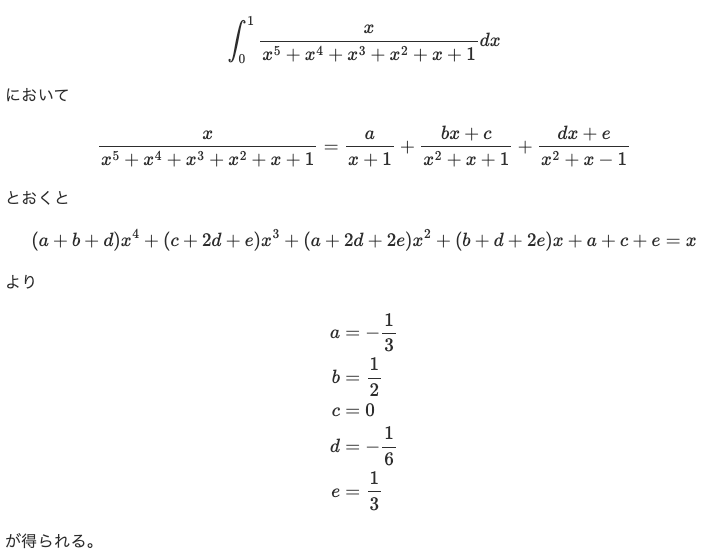
また,この問題は大学範囲の知識を使えばかなり簡単に解けるようになっています.

$\begin{array}{rcl} \int_{0}^{1} \frac{x}{x^{5} + x^{4} + x^{3} + x^{2} + x + 1} d x & = & \int_{0}^{1} \frac{(1 - x) x}{1 - x^{6}} d x \\ = & \sum_{n \geq 0} \int_{0}^{1} x^{6 n + 1} - x^{6 n + 2} d x \\ = & \frac{1}{6} \sum_{n \geq 0} \frac{1}{n + \frac{1}{3}} - \frac{1}{n + \frac{1}{2}} \\ = & \frac{ψ (\frac{1}{2}) - ψ (\frac{1}{3})}{6} \end{array}$

最後のψはディガンマ関数というものです.
このディガンマ関数の級数表示を最後の式変形で用いました.
積分で良く出てくる特殊関数の1つなので興味がある方は色々調べてみる事をおすすめします.
この関数は色々な方が紹介しているのでグーグルで検索するだけでたくさんページが出てきて参考になります.
オススメはまめけびさんの記事です.
この方は他にもたくさん参考になる記事を書かれているのでまじでオススメです.

$\begin{array}{r} \int_{0}^{1} \frac{\ln^{s - 1} \frac{1}{x}}{1 - x} d x = ζ (s) Γ (s) (Re s > 1) \end{array}$

これ実はめちゃくちゃ簡単なんですよね.
まずは解のそれぞれの関数を見てみましょう.
ゼータ関数
$\begin{array}{r} ζ (s) := \sum_{n = 1}^{\infty} \frac{1}{n} (Re s > 1) \end{array}$
ガンマ関数
$\begin{array}{r} Γ (s) := \int_{0}^{\infty} t^{s - 1} e^{- t} d t \end{array}$
ではこれらを踏まえて解説です.

$\begin{array}{rcl} \int_{0}^{1} \frac{\ln^{s - 1} \frac{1}{x}}{1 - x} d x & = & \int_{0}^{\infty} x^{s - 1} \frac{d x}{1 - e^{- x}} (\frac{1}{x} \to e^{x}) \\ = & \int_{0}^{\infty} x^{s - 1} \sum_{n = 0}^{\infty} e^{- (n + 1) x} d x (∵ \frac{1}{1 - z} = \sum_{n = 0}^{\infty} z^{n} (| z | < 1)) \\ = & \sum_{n = 1}^{\infty} \int_{0}^{\infty} \frac{x^{s - 1}}{n^{s}} e^{- x} d x (n x \to x) \\ = & \sum_{n = 1}^{\infty} \frac{1}{n^{s}} \cdot \int_{0}^{\infty} x^{s - 1} e^{- x} d x \\ = & ζ (s) Γ (s) \end{array}$

なんと最後定義そのままの形が出てきました.
実はこの積分1番最初に変形させて出てきた積分がかなり有名でゼータ関数の積分表示と呼ばれています.

$\begin{array}{r} \int_{0}^{1} \frac{x}{\sqrt{1 - x^{2}}} \ln \frac{1 + z x}{1 - z x} d x = π \frac{1 - \sqrt{1 - z^{2}}}{z} \end{array}$

これは初級にしてはかなり難しい問題です.
メインは級数展開ですね
対数関数の部分をマクローリン展開しベータ関数として計算することで級数を得られます.

$\begin{array}{rcl} \int_{0}^{1} \frac{x}{\sqrt{1 - x^{2}}} \ln \frac{1 + z x}{1 - z x} d x & = & \int_{0}^{1} \frac{x}{\sqrt{1 - x^{2}}} \sum_{n > 0} \frac{z^{n} x^{n} ((- 1)^{n - 1} + 1)}{n} \\ = & \sum_{n \geq 0} \frac{z^{2 n + 1}}{2 n + 1} \int_{0}^{1} \frac{x^{2 n + 2}}{\sqrt{1 - x^{2}}} d x \\ = & \frac{π}{2} \sum_{n \geq 0} \frac{z^{2 n + 1} (\frac{1}{2})_{n}}{(n + 1)!} \\ = & \frac{π}{2 z} \sum_{n \geq 0} \int_{0}^{z^{2}} x^{n} \frac{(\frac{1}{2})_{n}}{n!} d x \\ = & \frac{π}{2 z} \int_{0}^{z^{2}} (1 - x)^{- 1 / 2} d x \\ = & π \frac{1 - \sqrt{1 - z^{2}}}{z} \end{array}$

途中で一般化二項定理を用いた
またベータ関数の計算も出ているので調べてみると良いと思います.

$\begin{array}{r} \int_{0}^{\infty} \frac{\sin x}{x} e^{- a x} d x = \arctan \frac{1}{a} (a > 0) \end{array}$

まずこの積分では次のような手法を使います.
$\begin{array}{r} f (a) - f (b) = \int_{b}^{a} f^{'} (t) d t \end{array}$
今回どのように使うかというと次の2パターンが考えられます.
$\begin{array}{r} f (a) := \int_{0}^{\infty} \frac{\sin x}{x} e^{- a x} d x \end{array}$
$\begin{array}{r} ⑴ f (a) - f (0) = \int_{0}^{\infty} \frac{\sin x}{x} e^{- a x} - \int_{0}^{\infty} \frac{\sin x}{x} d x \end{array}$
$\begin{array}{r} ⑵ f (\infty) - f (a) = - \int_{0}^{\infty} \frac{\sin x}{x} e^{- a x} d x \end{array}$
⑴ではディリクレ積分が出てきてしまいますが⑵では今回の題意のみ与えられています.
なので簡単なために⑵で計算を勧めていきましょう.

$\begin{array}{rcl} \int_{0}^{\infty} \frac{\sin x}{x} e^{- a x} d x & = & \int_{0}^{\infty} \int_{a}^{\infty} \sin x e^{- t x} d t d x \\ = & \int_{a}^{\infty} \int_{0}^{\infty} \sin x e^{- x t} d x d t \\ = & \int_{a}^{\infty} \frac{1}{t^{2} + 1} d t \\ = & \int_{\arctan a}^{π / 2} d t (t \to \tan t) \\ = & \frac{π}{2} - \arctan a \end{array}$

この計算からわかるのは値からではなく式変形のみで
$\begin{array}{r} \int_{0}^{\infty} \frac{\sin x}{x} d x = \int_{0}^{\infty} \frac{d x}{1 + x^{2}} \end{array}$
が示せた訳です.
値を介さずにこういった積分間の等式を示すのは僕的にはかなり面白いと思っています.
またこれは似たような一般化があり,それが次のようなものです.