ポンスレ束の一般化～MMPとなかよく～
この記事は ポンスレ束について の続編です. まずはこちらをお読みください.
はじめに
前回の記事では, 等角共役が直線を円錐曲線に移すことを示し, 特に直線が三角形の外心を通るとき, 等角共役により得られる直角双曲線の漸近線がシムソン線を用いて特徴づけられることを紹介しました.
今回は等角共役, 9点円, シムソン線をそれぞれ円錐曲線の世界で定義しなおし,
ポンスレ束について
の定理5よりも強い主張を導きます. 記事の中でMMP(Method of Moving Points)を使うので, 知らない人はMMPを参照してください.
平行弦共役
まずは等角共役について確認します. 三角形$ABC$について$P,Q$が図1のような位置関係にあるとき, $Q$を$P$の等角共役といいます. 等角共役の性質として, 次のようなものがあります.
- 重心座標を用いて$[x:y:z]\mapsto [a^2yz:b^2zx:c^2xy]$と表現できる
- $P$が三角形$ABC$の外接円上$\Longleftrightarrow$ $Q$が無限遠点
- 等角共役による直線の像は$A,B,C$を通る円錐曲線である
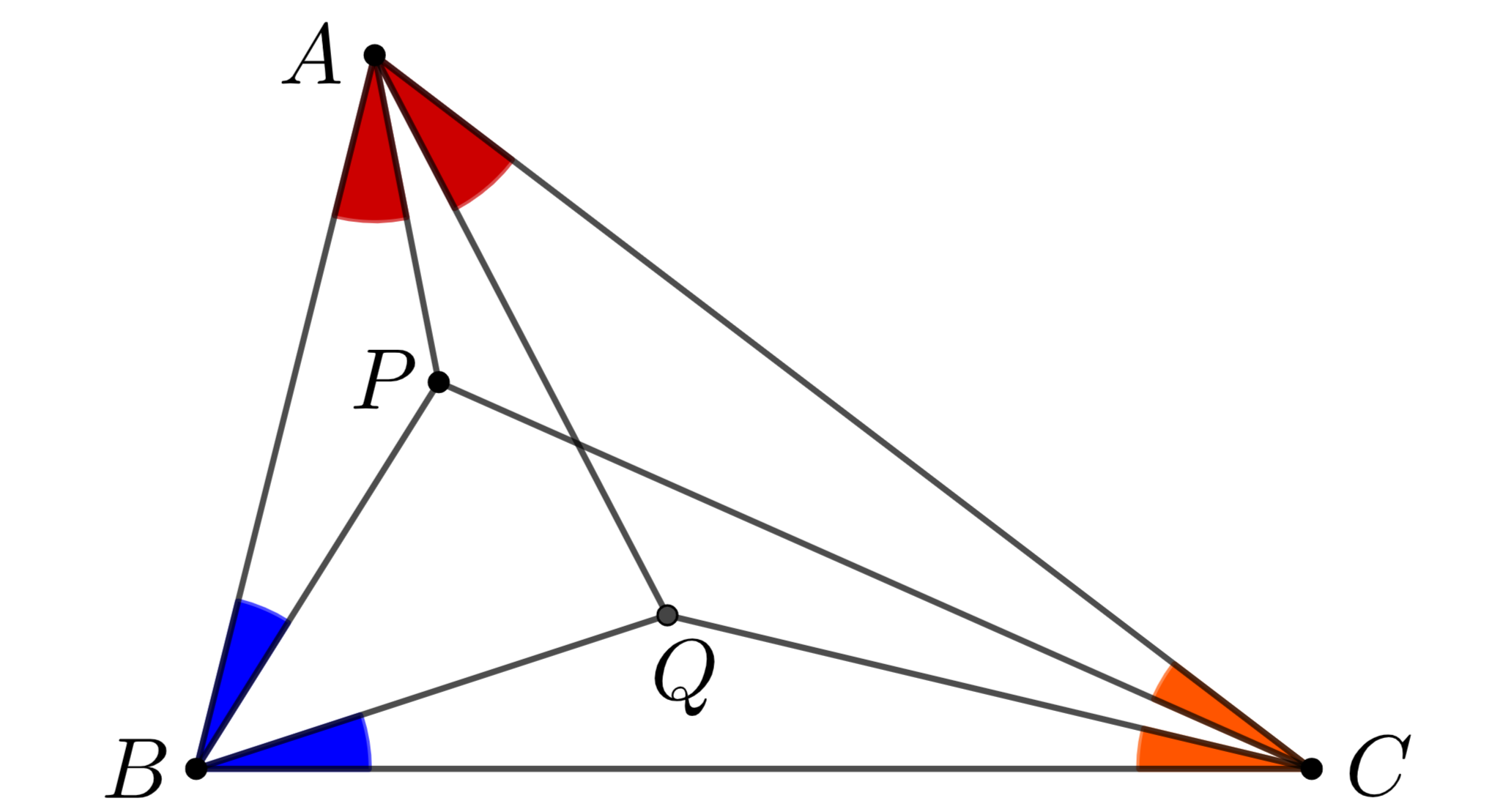Qの等角共役P
似たような性質をもつものに, 等長共役があります. 三角形$ABC$について$P,Q$が図2のような位置関係にあるとき, $Q$を$P$の等長共役といいます. 等長共役の性質としては, 次のようなものがあります.
- 重心座標を用いて$[x:y:z]\mapsto [yz:zx:xy]$と表現できる
- $P$が三角形$ABC$のシュタイナー外接楕円上$\Longleftrightarrow$ $Q$が無限遠点
- 等長共役による直線の像は$A,B,C$を通る円錐曲線である
Pの等長共役Q
これらを包含するのが次に示す平行弦共役です.
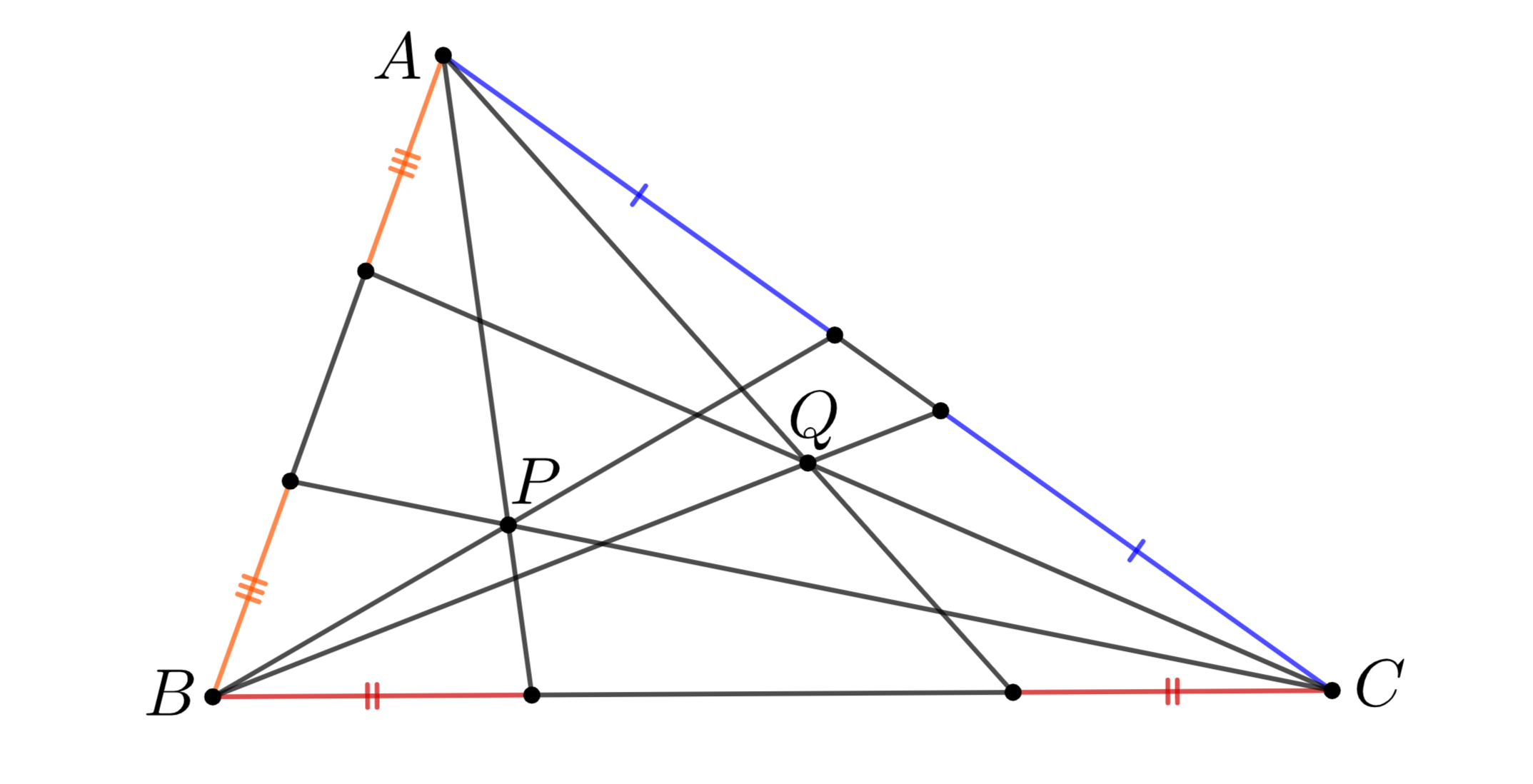
円錐曲線$\mathcal{C}$に内接する三角形$ABC$と点$P$をとる. $AP$が$\mathcal{C}$と再び交わる点を$A_1$, $A_1$を通り$BC$に平行な直線が$\mathcal{C}$と再び交わる点を$A_2$とし, 同様に$B_1,B_2,C_1,C_2$を定める. このとき, $AA_2,BB_2,CC_2$は1点で交わり, 交点$Q$を$P$の平行弦共役という.
Pの平行弦共役Q
$\mathcal{C},\triangle ABC,A_1$を固定し, $AA_1$上を$P$が動くとする. このとき, 次の2つはそれぞれ射影写像である.
$$
P\mapsto BP\mapsto B_1\mapsto B_2\mapsto BB_2\mapsto BB_2\cap AA_2
$$
$$
P\mapsto CP\mapsto C_1\mapsto C_2\mapsto CC_2\mapsto CC_2\cap AA_2
$$
これらが写像として一致することを示すには, $AA_1$上の相異なる3点で一致することを確かめればよい. $P=A, AA_1\cap BC$のときは明らか. $P=A_1$のとき, $ACBB_2PA_2$と$ABCC_2PA_2$にパスカルの定理を適用することで$AA_2\parallel BB_2\parallel CC_2$を得る. 以上より示された.
$\mathcal{C}:pyz+qzx+rxy=0$のとき, 平行弦共役は$[x:y:z]\mapsto [pyz:qzx:rxy]$で表せることが計算により分かります. 従って, $(p,q,r)=(a^2,b^2,c^2)$つまり$\mathcal{C}$が外接円のときは等角共役, $(p,q,r)=(1,1,1)$つまり$\mathcal{C}$がシュタイナー外接楕円のときは等長共役となり, 確かに両者を含んでいます.
平行弦共役が$[x:y:z]\mapsto [pyz:qzx:rxy]$で表せることから, 前編で紹介した等角共役の性質は平行弦共役でも全く同様に示すことができます.
$P,Q$の平行弦共役をそれぞれ$P',Q'$とするとき, $X=PQ\cap P'Q'$と$Y=PQ'\cap P'Q$は互いに平行弦共役である.
三角形$ABC$と$A,B,C$を通らない直線$l$上の点$P$をとる. $P$が$l$上を動くとき, $P$の平行弦共役は$ABC$に外接する円錐曲線を描く.
$l$の像となる円錐曲線の形状は次のように判別できる.
- $l$が$\mathcal{C}$と交わらないとき, 楕円
- $l$と$\mathcal{C}$が接するとき, 放物線
- $l$と$\mathcal{C}$が2点で交わるとき, 双曲線
平行弦共役が$[x:y:z]\mapsto [pyz:qzx:rxy]$で表せることを示せ.
9点円錐曲線
次に, 9点円の一般化である9点円錐曲線を定義します.
どの3つも共線でない4点$A,B,C,D$をとる. $A,B,C,D$を通る円錐曲線$\mathcal{C}$について, その中心は$\mathcal{C}$の取り方に依らずある円錐曲線上にある. この円錐曲線を9点円錐曲線という.
$\mathcal{C}$の中心を$X$とし,$AB,BC,CD,DA$の中点を$P,Q,R,S$とする. このとき, $XP,XQ,XR,XS$の極はそれぞれ$AB,BC,CD,DA$方向の無限遠点であり, $(XP,XQ;XR,XS)$は$\mathcal{C}$の取り方に依らない. よって主張は示された.
どの3つも共線でない4点$A,B,C,D$に対し, 以下の9点は同一円錐曲線上にある.
- $AB,AC,AD,BC,BD,CD$の中点
- $AB\cap CD, AC\cap BD, AD\cap BC$
A,B,C,Dの9点円錐曲線
$AB$の中点について$C,D$と対称な点を$C',D'$として$ACDBC'D'$にパスカルの定理を適用すると, $AB$の中点を中心としてこれら6点を通る円錐曲線の存在がわかる. ほかの中点についても同様.
さらに, $AB\cup CD, AC\cup BD, AD\cup BC$は退化した双曲線であり, これらの中心はそれぞれ$AB\cap CD, AC\cap BD, AD\cap BC$とみなせる.
以上より, これら9点はすべて9点円錐曲線上にある.
特に, $A,B,C,D$が垂心系をなすとき9点円錐曲線は三角形$ABC$の9点円と一致します. このとき, 定理4によれば9点円は4点$A,B,C,D$を通る円錐曲線, つまり直角双曲線（前編の補題4を参照）の中心の軌跡であり, これは前編の定理5の前半の主張と同じです.
余談ですが, どの3つも共点でない4直線に対し, それらに接する円錐曲線の中心の軌跡は4直線のなす完全四辺形のニュートン線になります.
三角形$ABC$とその重心$G$について, $A,B,C,G$の9点円錐曲線はシュタイナー内接楕円であることを確認せよ.
4点$A,B,C,D$の9点円錐曲線の中心は$AD$の中点と$BC$の中点を結ぶ線分の中点であることを示せ.
略解
$CA,CB,DB,DA$の中点が平行四辺形をなすことから従う.どの3つも共線でない5点$A,B,C,D,E$について, $ABCD,BCDE,CDEA,DEAB,EABC$の9点円錐曲線は1点で交わることを示せ.
略解
$A,B,C,D,E$を通る円錐曲線が一意に存在し, この中心を5つの9点円錐曲線が共有する.Japan TST 2016-12 において, 四角形$APOS,BQOP,CROQ,DSOR$のニュートン線が1点で交わることを示せ. また, この交点はどのような点か.
略解
ブリアンションの定理の逆より$AB,BC,CD,DA,PR,QS$のすべてに接する円錐曲線が存在する. この中心を4本のニュートン線が共有する.コニック・シムソン線とコニック・シュタイナー線
三角形$ABC$と点$D$に対し, $A,B,C,D$の9点円錐曲線を$D$中心で2倍拡大したものを外接9点円錐曲線とよび, この曲線上の点についてシムソン線の類似物を定めます.
三角形$ABC$と点$D$について, 外接9点円錐曲線$\mathcal{C}$上に点$P$をとる. $AD,BD,CD$が$\mathcal{C}$と再び交わる点をそれぞれ$D_A,D_B,D_C$とし, $PD_A,PD_B,PD_C$と$BC,CA,AB$の交点をそれぞれ$X,Y,Z$とするとき, 3点$X,Y,Z$は同一直線上にある. この3点を通る直線をコニック・シュタイナー線といい, コニック・シュタイナー線を$P$中心で$\dfrac{1}{2}$倍拡大したものをコニック・シムソン線という.
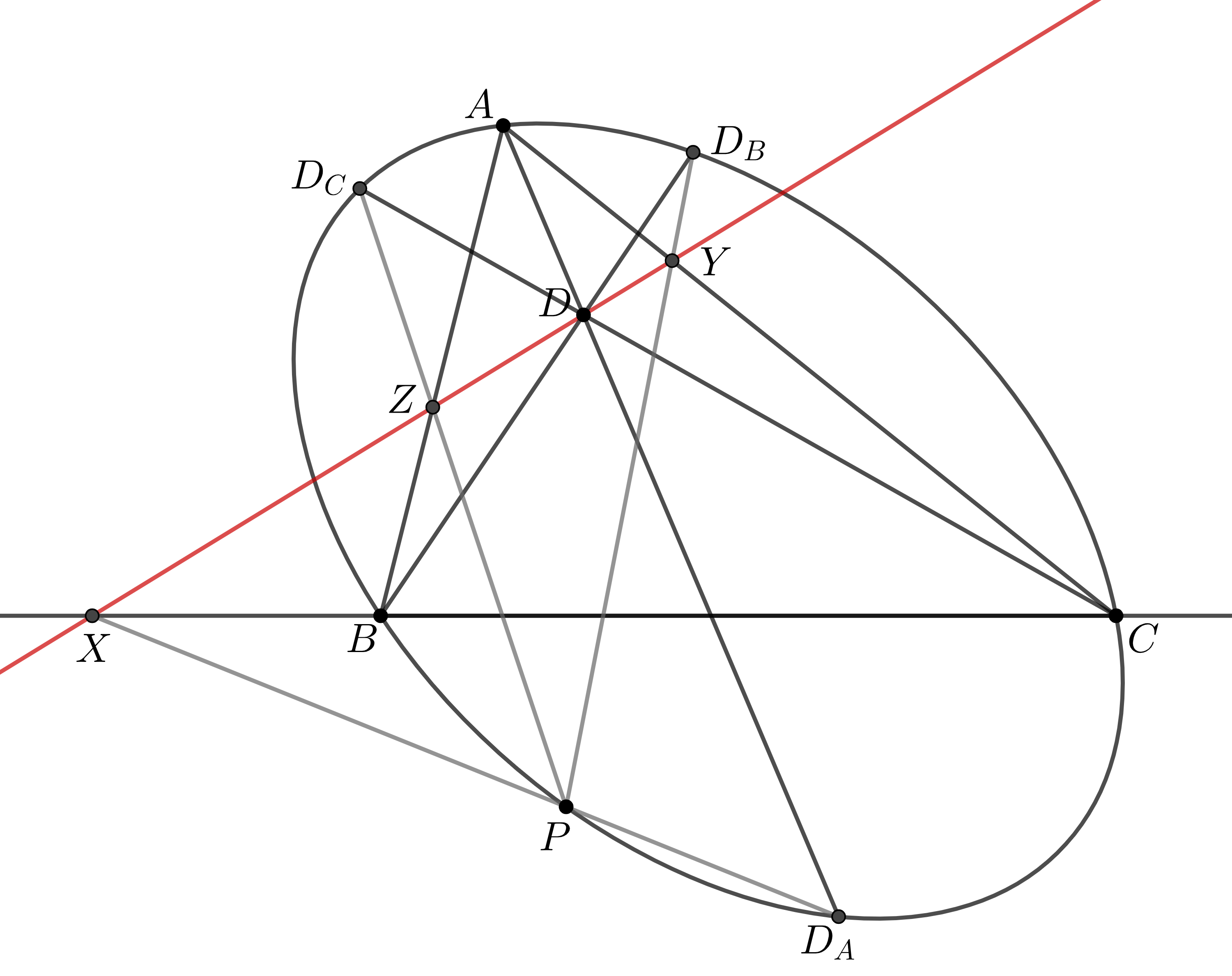Pにおけるコニック・シムソン線
$BCAD_APD_B$にパスカルの定理を適用すると, $D$が$XY$上にあることがわかる. 同様にして$D$が$YZ$上にあることも従うのでよい.
$D$が三角形$ABC$の垂心のとき, コニック・シムソン線は通常のシムソン線と一致することを確認せよ.
中心と漸近線の特徴づけ
三角形$ABC$と点$D$について, 外接9点円錐曲線$\mathcal{C}$上の点$P,Q$が中心$O$について対称であるとする. このとき, 平行弦共役による$PQ$の像$\mathcal{H}$の中心は9点円錐曲線上にあり, その漸近線は$P,Q$におけるコニック・シムソン線に一致する.
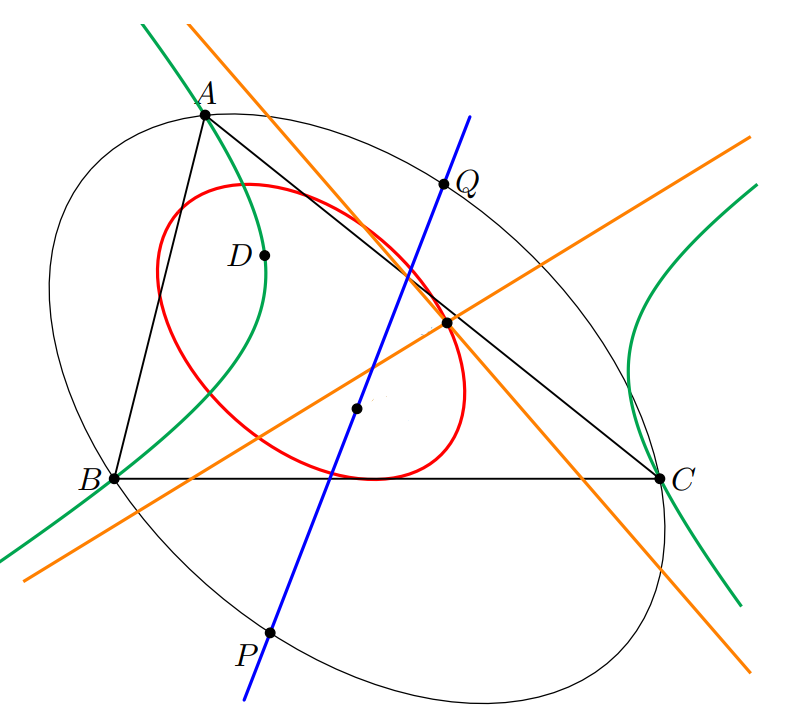\mathcal{H}の漸近線(橙)
$\mathcal{H}$と円$ABC$が再び交わる点を$E$とし, $P,Q$の平行弦共役をそれぞれ$P',Q'$とする. 次の3ステップで示す.
- $\mathcal{H}$の中心は9点円錐曲線上にあり, 特に$DE$の中点である.
- $P,Q$におけるコニック・シュタイナー線は$\mathcal{H}$の漸近線とそれぞれ平行である.
- $P,Q$におけるコニック・シムソン線は$\mathcal{H}$の中心で交わる.
(1)を示す. $\mathcal{H}$の中心が9点円錐曲線上にあることは定理3,4よりただちに従う. さらに, $\mathcal{H}$の中心について$D$と対称な点を$E'$とすると, 対称性より$E'$は$\mathcal{H}$上にあり, さらに$\mathcal{C}$の定義よりこれは$\mathcal{C}$上でもある. よって示された.
(2)を示す. $P$におけるコニック・シュタイナー線方向の無限遠点が$Q'$に一致することを示せばよい. 定理5と同様に$D_A,D_B,D_C,X,Y,Z$を定め, $Q$を通り$BC$に平行な直線が$\mathcal{C}$と再び交わる点を$Q_2$とする. ここで$A,B,C,D$を固定し, $P$が$\mathcal{C}$上を動くとする. このとき, 次の2つはそれぞれ射影写像である.
$$
P\mapsto PD_A\mapsto X\mapsto DX\mapsto m
$$
$$
P\mapsto Q\mapsto Q_2\mapsto AQ_2
$$
ただし, $m$は$A$を通り$DX$に平行な直線であるとする. これらが写像として一致することを示すには, $\mathcal{C}$上の相異なる3点で一致することを確かめればよい. $BC$の中点を$M$とし, $Ad$の中点を$N$とする. また, $ADとBC$の交点を$A_1$とする. まず$P=A$のときを示す. このとき, 9点円錐曲線の中心が$MN$の中点であることから$DMON$は平行四辺形であり, これより$DQ$の中点は$M$である. よって$A_1M\parallel D_AQ$であるのでよい. 次に$P=B$のときを示す. このとき, $BCQQ_2$と$ADBQ_2$はともに平行四辺形であることから従う. $P=C$のときも同様である. 以上より$P=A,B,C$での成立が示されたので, (2)は示された.
最後に(3)を示す. $P,Q$に補題2を用いると, $PQ\cap P'Q'$と$PQ'\cap P'Q$は互いに等角共役である. $PQ\cap P'Q'$は$PQ$方向の無限遠点であるから, $PQ'\cap P'Q=E$を得る. ここで, (2)より$PQ',P'Q$はそれぞれ$P,Q$におけるコニック・シュタイナー線に平行な直線である. コニック・シムソン線はコニック・シュタイナー線を$\dfrac{1}{2}$倍に相似拡大したものであり, 定理5よりコニック・シュタイナー線は定点$D$を通るので, $P,Q$におけるコニック・シムソン線は$DE$の中点, つまり$\mathcal{H}$の中心で交わる.
以上より, $P,Q$におけるコニック・シムソン線は漸近線に他ならない.
