【相対論】Goldberg-Sachsの定理
相対論で有名な定理の一つであるGoldberg-Sachsの定理を証明します。この記事はPetrov分類、Newmann-Penrose formalismを前提知識としています。
4次元Einstein時空の近傍$U$において、shearfree geodesic null congruenceが存在することと$U$上でWeylテンソルがalgebraically specialであることは同値である。
この記事ではshearfree geodesic null congruenceとNewman-Penrose formalismを簡単に復習してからGoldberg-Sachsの定理をもう少し精密化して証明します。
Newman-Penrose formalism
Newman-Penrose formalism 3 の内容を使いますが、Goldberg-Sachsの定理に必要な事項だけここにまとめます。
4次元時空$(M,g)$のnull tetradを$\{m,\bar m,l,k\}$とします。このときスピン係数を
\begin{align}
&\alpha = \frac{1}{2}[g(\nabla_{\bar{m}}k,\ell) - g(\nabla_{\bar{m}}\bar m,m)] \\
&\beta = \frac{1}{2}[g(\nabla_mk,\ell) - g(\nabla_m\bar{m},m)] \\
&\gamma = \frac{1}{2}[g(\nabla_\ell k,\ell) - g(\nabla_\ell\bar{m},m)] \\
&\varepsilon = \frac{1}{2}[g(\nabla_kk,\ell) - g(\nabla_k\bar{m},m)] \\
&\mu = g(\nabla_m\ell,\bar m),\ \
\lambda = g(\nabla_{\bar m}\ell,\bar m) \\
&\nu = g(\nabla_\ell\ell,\bar m),\ \
\pi = g(\nabla_k\ell,\bar m) \\
&\sigma = g(\nabla_mk,m),\ \
\rho = g(\nabla_{\bar m}k,m) \\
&\tau = g(\nabla_\ell k,m),\ \
\kappa = g(\nabla_kk,m) \\
\end{align}
で定義します。
ワイルテンソル$W$は
\begin{align}
& W_{abcd} = R_{abcd} + g_{ad}\text{P}_{cb} - g_{ac}\text{P}_{db} + g_{bc}\text{P}_{da} - g_{bd}\text{P}_{ca}\\
& \text{P}_{ab} = \frac{1}{2}R_{ab} - \frac{1}{12}Rg_{ab}
\end{align}
で与えられ、実10次元の自由度を持ち、Weylスカラーと呼ばれる5つの複素数
\begin{align}
&\Psi_0=W(k,m,k,m),\Psi_1=W(k,l,k,m),\Psi_2=W(k,m,l,\bar m)\\
&\Psi_3=W(l,k,l,\bar m),\Psi_4=W(l,\bar m,l,\bar m)
\end{align}
を使ってWeylテンソルの任意の成分は表されます。
Petrov分類1
で解説してますが、$\Psi_0=\Psi_1=0$のとき、その時空、または近傍、または時空点はalgebraically specialと呼ばれます。
このとき単純な計算により以下が成り立つことが分かります。
\begin{align}
&(f1)\ \ [m,k] = (\bar{\rho} + \bar{\varepsilon} - \varepsilon)m + \sigma\bar{m} + \kappa l + (\bar{\alpha} + \beta + \bar{\pi})k\\
&(f2)\ \ k\beta = m\varepsilon - \bar{\alpha}\varepsilon - \beta\bar{\varepsilon} - \gamma\kappa - \kappa\mu - \varepsilon\bar{\pi} - \beta\bar{\rho} - \alpha\sigma + \pi\sigma - \Psi_1 \\
&(f3)\ \ m\rho = \bar{m}\sigma + \kappa\bar{\mu} - \kappa\mu + \bar{\alpha}\rho + \beta\rho - 3\alpha\sigma + \bar{\beta}\sigma - \bar\rho\tau + \rho\tau - \Psi_1 - \text{P}_{14} \\
&(f4)\ \ k\tau = l\kappa - \bar{\gamma}\kappa - 3\gamma\kappa + \bar{\pi}\rho + \pi\sigma - \sigma\bar{\tau} - \bar{\varepsilon}\tau + \varepsilon\tau - \rho\tau - \Psi_1 + \text{P}_{14} \\
&(f5)\ \ m\Psi_1 = l\Psi_0 - k\text{P}_{11} + m\text{P}_{14} - 4\gamma\Psi_0 + \mu\Psi_0 + 2\beta\Psi_1 - 3\sigma\Psi_2 + 4\tau\Psi_1 - 2\kappa\text{P}_{13} + 2\varepsilon\text{P}_{11} - 2\bar{\varepsilon}\text{P}_{11} - 2\beta\text{P}_{14} - 2\bar{\pi}\text{P}_{14} + \bar{\lambda}\text{P}_{44} - \bar{\rho}\text{P}_{11} - \sigma\text{P}_{12} + \sigma\text{P}_{34} \\
&(f6)\ \ k\Psi_1 = -\bar{m}\Psi_0 - k\text{P}_{14} + m\text{P}_{44} + 4\alpha\Psi_0 + \pi\Psi_0 + 2\varepsilon\Psi_1 - 3\kappa\Psi_2 - 4\Psi_1\rho + \bar{\kappa}\text{P}_{11} + \kappa\text{P}_{12} + 2\varepsilon\text{P}_{14} - \kappa\text{P}_{34} - 2\bar{\alpha}\text{P}_{44} - 2\beta\text{P}_{44} - \bar{\pi}\text{P}_{44} - 2\rho\text{P}_{14} - 2\sigma\text{P}_{24}\\
&(f7)\ \ l\Psi_1 = m\Psi_2 + k\text{P}_{13} - m\text{P}_{34} + \nu\Psi_0 + 2\gamma\Psi_1 - 2\mu\Psi_1 - 2\sigma\Psi_3 - 3\tau\Psi_2 - \pi\text{P}_{11} - \bar{\pi}\text{P}_{12} + 2\bar{\varepsilon}\text{P}_{13} + \mu\text{P}_{14} + \bar{\lambda}\text{P}_{24} + \kappa\text{P}_{33} + \bar{\pi}\text{P}_{34} + \bar{\rho}\text{P}_{13} + \sigma\text{P}_{23} \\
&(f8)\ \ m\bar{\Psi}_1 = -k\bar{\Psi}_2 + k\text{P}_{12} - \bar{m}\text{P}_{14} + \bar{\lambda}\bar{\Psi}_0 + 2\bar{\alpha}\bar{\Psi}_1 + 2\bar{\pi}\bar{\Psi}_1 + 2\bar{\kappa}\bar{\Psi}_3 - 3\bar{\rho}\bar{\Psi}_2 + \kappa\text{P}_{23} + \bar{\pi}\text{P}_{24} + \bar{\kappa}\text{P}_{13} + 2\alpha\text{P}_{14} + \pi\text{P}_{14} - \bar{\mu}\text{P}_{44} + \rho\text{P}_{12} - \rho\text{P}_{34} + \bar{\sigma}\text{P}_{11} \\
&(f9)\ \ l\Psi_2 = -m\Psi_3 + l\text{P}_{12} - \bar{m}\text{P}_{13} + 2\nu\Psi_1 - 3\mu\Psi_2 - 2\beta\Psi_3 + 2\tau\Psi_3 + \sigma\Psi_4 + \lambda\text{P}_{11} + \bar\mu\text{P}_{12} - 2\bar{\beta}\text{P}_{13} + \nu\text{P}_{14} + \bar{\nu}\text{P}_{24} - \rho\text{P}_{33} - \bar{\mu}\text{P}_{34} + \tau\text{P}_{23} + \bar{\tau}\text{P}_{13} \\
&(f10)\ \ k\Psi_3 = \bar{m}\Psi_2 + l\text{P}_{24} - \bar{m}\text{P}_{34} - 2\lambda\Psi_1 - 3\pi\Psi_2 - 2\varepsilon\Psi_3 + \kappa\Psi_4 - 2\rho\Psi_3 + \lambda\text{P}_{14} + \rho\text{P}_{23} - 2\bar{\gamma}\text{P}_{24} + \bar{\mu}\text{P}_{24} + \nu\text{P}_{44} + \bar{\sigma}\text{P}_{13} - \tau\text{P}_{22} - \bar{\tau}\text{P}_{12} + \bar{\tau}\text{P}_{34}
\end{align}
Shearfree geodesic null congruence
$k$はnullベクトル場なのでその積分曲線はnull curveの束となり、これはnull congruenceと呼ばれます。さらに
\begin{align}
\nabla_k k = (\varepsilon + \bar{\varepsilon})k + \bar{\kappa}m + \kappa\bar{m}
\end{align}
が成り立つので、$\kappa=0$のとき、$k$の積分曲線は測地線になります。このような状況を$k$はgeodesic null congruenceを定めると言います。
また$\sigma = g(\nabla_mk,m)$は$k$のshearと呼ばれます。この量は$k$の作るnull congruenceのspacelikeな2次元断面がどのように“へしゃげる”かを表しています(詳しくはnull congruenceのshearについての記事)。
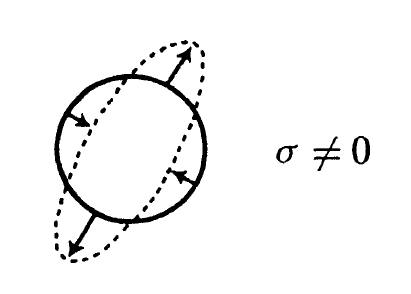 shear
shear
$\sigma=0$のとき、このnull congruenceは断面が変形せずに進んで行き、shearfreeであると言います。。$\kappa=\sigma=0$のとき、$k$はshearfree geodesic null congruenceを生成すると言います。
精密化されたGoldberg-Sachsの定理
Einstein metricならば
\begin{align}
P_{11}=P_{14}=P_{44}=\text{P}_{13} = \text{P}_{22} = \text{P}_{23} = \text{P}_{24} = \text{P}_{33} = \text{P}_{12} - \text{P}_{34} = 0
\end{align}
となりますが、この条件のうちで必要最小限の条件のみ仮定したものが以下の定理です。
$(M,g)を$4次元時空とする。
(1)$P_{11}=P_{14}=P_{44}=0$かつ$\kappa=\sigma=0$であるとき、$\Psi_0=\Psi_1=0$である。
(2)$g$がEinsteinでありかつ共形平坦でないとき、$\Psi_0=\Psi_1=0$ならば$\kappa=\sigma=0$である。
(1)
\begin{align}
m\kappa = k\sigma + \bar{\alpha}\kappa + 3\beta\kappa + \kappa\bar{\pi} - 3\varepsilon\sigma + \bar{\varepsilon}\sigma + \rho\sigma + \bar{\rho}\sigma + \kappa\tau + \Psi_0
\end{align}
より$\kappa=\sigma=0$より$\Psi_0=0$である。
また
\begin{align}
& m\Psi_1 = l\Psi_0 - k\text{P}_{11} + m\text{P}_{14} - 4\gamma\Psi_0 + \mu\Psi_0 + 2\beta\Psi_1 - 3\sigma\Psi_2 + 4\tau\Psi_1 - \\
& \qquad 2\kappa\text{P}_{13} + 2\varepsilon\text{P}_{11} - 2\bar{\varepsilon}\text{P}_{11} - 2\beta\text{P}_{14} - 2\bar{\pi}\text{P}_{14} + \bar{\lambda}\text{P}_{44} - \bar{\rho}\text{P}_{11} - \sigma\text{P}_{12} + \sigma\text{P}_{34} \\
& k\Psi_1 = -\bar{m}\Psi_0 - k\text{P}_{14} + m\text{P}_{44} + 4\alpha\Psi_0 + \pi\Psi_0 + 2\varepsilon\Psi_1 - 3\kappa\Psi_2 - 4\Psi_1\rho + \bar{\kappa}\text{P}_{11} + \\
& \qquad \kappa\text{P}_{12} + 2\varepsilon\text{P}_{14} - \kappa\text{P}_{34} - 2\bar{\alpha}\text{P}_{44} - 2\beta\text{P}_{44} - \bar{\pi}\text{P}_{44} - 2\rho\text{P}_{14} - 2\sigma\text{P}_{24}
\end{align}
より$P_{11}=P_{14}=P_{44}=\kappa=\sigma=0$のとき
\begin{align}
& m\Psi_1 = 2\beta\Psi_1 + 4\tau\Psi_1\\
& k\Psi_1 = 2\varepsilon\Psi_1 - 4\Psi_1\rho
\end{align}
である。よって
\begin{align}
&[m, k]\Psi_1 = 2m((\varepsilon - 2\rho)\Psi_1) - 2k((\beta + 2\tau)\Psi_1)
\end{align}
であり、
\begin{align}
(f1)\ \ [m,k] = (\bar{\rho} + \bar{\varepsilon} - \varepsilon)m + \sigma\bar{m} + \kappa l + (\bar{\alpha} + \beta + \bar{\pi})k
\end{align}
を使うと
\begin{align}
&2(\bar\rho + \bar\varepsilon - \varepsilon)(\beta + 2\tau)\Psi_1 + 2(\bar\alpha + \beta + \bar\pi)(\varepsilon - 2\rho)\Psi_1 \\
&=2m((\varepsilon - 2\rho)\Psi_1) - 2k((\beta + 2\tau)\Psi_1)\\
&\therefore\ \left(2m(\varepsilon-2\rho)-2k(\beta+2\tau)+2(\varepsilon-\bar\varepsilon-\bar\rho)(\beta+2\tau)-2(\bar\alpha+\beta+\bar\pi)(\varepsilon-2\rho)\right)\Psi_1 = 0
\end{align}
また
\begin{align}
&(f2)\ \ k\beta = m\varepsilon - \bar{\alpha}\varepsilon - \beta\bar{\varepsilon} - \gamma\kappa - \kappa\mu - \varepsilon\bar{\pi} - \beta\bar{\rho} - \alpha\sigma + \pi\sigma - \Psi_1 \\
&(f3)\ \ m\rho = \bar{m}\sigma + \kappa\bar{\mu} - \kappa\mu + \bar{\alpha}\rho + \beta\rho - 3\alpha\sigma + \bar{\beta}\sigma - \bar\rho\tau + \rho\tau - \Psi_1 - \text{P}_{14} \\
&(f4)\ \ k\tau = l\kappa - \bar{\gamma}\kappa - 3\gamma\kappa + \bar{\pi}\rho + \pi\sigma - \sigma\bar{\tau} - \bar{\varepsilon}\tau + \varepsilon\tau - \rho\tau - \Psi_1 + \text{P}_{14} \\
\end{align}
は
\begin{align}
& k\beta = m\varepsilon - \bar{\alpha}\varepsilon - \beta\bar{\varepsilon} - \varepsilon\bar{\pi} - \beta\bar{\rho} - \Psi_1 \\
& m\rho = \bar{\alpha}\rho + \beta\rho - \bar\rho\tau + \rho\tau - \Psi_1 \\
& k\tau = \bar{\pi}\rho - \bar{\varepsilon}\tau + \varepsilon\tau - \rho\tau - \Psi_1 \\
\end{align}
となるから、これらを代入して微分項を消去すると、$\Psi_1$以外の項はちょうど消えて
\begin{align}
10\Psi_1^2=0
\end{align}
となり、$\Psi_1=0$が分かる。
(2)
Einstein条件
\begin{align}
P_{11}=P_{14}=P_{44}=\text{P}_{13} = \text{P}_{22} = \text{P}_{23} = \text{P}_{24} = \text{P}_{33} = \text{P}_{12} - \text{P}_{34} = 0
\end{align}
と$\Psi_0=\Psi_1=0$が成り立つとする。
\begin{align}
(f5) & m\Psi_1 = l\Psi_0 - k\text{P}_{11} + m\text{P}_{14} - 4\gamma\Psi_0 + \mu\Psi_0 + 2\beta\Psi_1 - 3\sigma\Psi_2 + 4\tau\Psi_1 - 2\kappa\text{P}_{13} + 2\varepsilon\text{P}_{11} - 2\bar{\varepsilon}\text{P}_{11} - 2\beta\text{P}_{14} - 2\bar{\pi}\text{P}_{14} + \bar{\lambda}\text{P}_{44} - \bar{\rho}\text{P}_{11} - \sigma\text{P}_{12} + \sigma\text{P}_{34} \\
(f6) & k\Psi_1 = -\bar{m}\Psi_0 - k\text{P}_{14} + m\text{P}_{44} + 4\alpha\Psi_0 + \pi\Psi_0 + 2\varepsilon\Psi_1 - 3\kappa\Psi_2 - 4\Psi_1\rho + \bar{\kappa}\text{P}_{11} + \kappa\text{P}_{12} + 2\varepsilon\text{P}_{14} - \kappa\text{P}_{34} - 2\bar{\alpha}\text{P}_{44} - 2\beta\text{P}_{44} - \bar{\pi}\text{P}_{44} - 2\rho\text{P}_{14} - 2\sigma\text{P}_{24}\\
\end{align}
より
\begin{align}
\sigma\Psi_2=\kappa\Psi_2 =0
\end{align}
が得られる。
$\kappa=\sigma=0$なら証明は終わりなので、$\kappa$または$\sigma$が0でない開集合上で考える。
このとき$\Psi_0=\Psi_1=\Psi_2=0$である。
\begin{align}
(f7) & l\Psi_1 = m\Psi_2 + k\text{P}_{13} - m\text{P}_{34} + \nu\Psi_0 + 2\gamma\Psi_1 - 2\mu\Psi_1 - 2\sigma\Psi_3 - 3\tau\Psi_2 - \pi\text{P}_{11} - \bar{\pi}\text{P}_{12} + 2\bar{\varepsilon}\text{P}_{13} + \mu\text{P}_{14} + \bar{\lambda}\text{P}_{24} + \kappa\text{P}_{33} + \bar{\pi}\text{P}_{34} + \bar{\rho}\text{P}_{13} + \sigma\text{P}_{23} \\
(f8) & m\bar{\Psi}_1 = -k\bar{\Psi}_2 + k\text{P}_{12} - \bar{m}\text{P}_{14} + \bar{\lambda}\bar{\Psi}_0 + 2\bar{\alpha}\bar{\Psi}_1 + 2\bar{\pi}\bar{\Psi}_1 + 2\bar{\kappa}\bar{\Psi}_3 - 3\bar{\rho}\bar{\Psi}_2 + \kappa\text{P}_{23} + \bar{\pi}\text{P}_{24} + \bar{\kappa}\text{P}_{13} + 2\alpha\text{P}_{14} + \pi\text{P}_{14} - \bar{\mu}\text{P}_{44} + \rho\text{P}_{12} - \rho\text{P}_{34} + \bar{\sigma}\text{P}_{11} \\
\end{align}
より
\begin{align}
&0 = - m\text{P}_{34} - 2\sigma\Psi_3 = - 2\sigma\Psi_3\\
&0= k\text{P}_{12} + 2\bar{\kappa}\bar{\Psi}_3 =2\bar{\kappa}\bar{\Psi}_3
\end{align}
なので、
\begin{align}
\sigma\Psi_3=\kappa\Psi_3 =0
\end{align}
である。
$\kappa=\sigma=0$なら証明は終わりなので、$\kappa$または$\sigma$が0でない開集合上で考える。
このとき$\Psi_0=\Psi_1=\Psi_2=\Psi_3=0$である。
\begin{align}
(f9) & l\Psi_2 = -m\Psi_3 + l\text{P}_{12} - \bar{m}\text{P}_{13} + 2\nu\Psi_1 - 3\mu\Psi_2 - 2\beta\Psi_3 + 2\tau\Psi_3 + \sigma\Psi_4 + \lambda\text{P}_{11} + \bar\mu\text{P}_{12} - 2\bar{\beta}\text{P}_{13} + \nu\text{P}_{14} + \bar{\nu}\text{P}_{24} - \rho\text{P}_{33} - \bar{\mu}\text{P}_{34} + \tau\text{P}_{23} + \bar{\tau}\text{P}_{13} \\
(f10) & k\Psi_3 = \bar{m}\Psi_2 + l\text{P}_{24} - \bar{m}\text{P}_{34} - 2\lambda\Psi_1 - 3\pi\Psi_2 - 2\varepsilon\Psi_3 + \kappa\Psi_4 - 2\rho\Psi_3 + \lambda\text{P}_{14} + \rho\text{P}_{23} - 2\bar{\gamma}\text{P}_{24} + \bar{\mu}\text{P}_{24} + \nu\text{P}_{44} + \bar{\sigma}\text{P}_{13} - \tau\text{P}_{22} - \bar{\tau}\text{P}_{12} + \bar{\tau}\text{P}_{34}
\end{align}
より
\begin{align}
\sigma\Psi_4 = \kappa\Psi_4 =0
\end{align}
である。共形平坦でないことを仮定しているから$\Psi_4\ne0$である。よって$\sigma=\kappa=0$である。
定理1(Goldberg-Sachs)
4次元Einstein時空の近傍$U$において、shearfree geodesic null congruenceが存在することと$U$上でWeylテンソルがalgebraically specialであることは同値である。
4次元Einstein時空の近傍$U$において、shearfree geodesic null congruenceが存在するならば、algebraically specialであることは定理2(1)より分かる。
逆に、4次元Einstein時空の近傍$U$において、もし共形平坦でなければ、定理2(2)より、algebraically specialならばshearfree geodesic null congruenceが存在することが分かる。
共形平坦の場合は、Minkowski時空と共形同値となり、自明にalgebraically specialである。またMinkowski時空のgeodesic null congruenceは明らかにshearfreeである。さらに共形変換によってshearfree geodesic null congruenceという性質は不変なので、Minkowski時空と共形同値な時空はshearfree geodesic null congruenceを無数に持つ。
参考文献
A. ROD GOVER, C. DENSON HILL, AND PAWEL NUROWSKI SHARP VERSION OF THE GOLDBERG-SACHS THEOREM
B.O'Neill, Geometry of Kerr Black Holes
