インスタントンとトンネル効果 (1) : 経路積分とWKB近似

インスタントンとトンネル効果

インスタントンは、Euclid空間における理論の基底状態間を結ぶ古典解です。この解は虚時間の特定の領域に局在するためその名がついています。

経路積分におけるWKB（Wentzel–Kramers–Brillouin）近似は、$\hbar$のべき展開を行い、古典解のまわりで量子効果を取り入れる近似です。ここでは二重井戸型ポテンシャルにおけるインスタントン解の周りの量子効果を取り入れることで、基底状態のエネルギーを近似的に求めます。

記事は3回に分け、今回はWKB近似まで記します。本記事はRef.Sakita1986に基づきます。

ちなみに標準的な教科書におけるWKB近似の説明とは異なることをご承知ください。ここではインスタントンとトンネル効果の関係に必要な経路積分における議論のみ行い、接続の問題など（例えばRef.Muto参照のこと）は扱いません。

経路積分

まずごく簡単に経路積分を説明します。

今、ある時刻$t'$で波動関数がわかっているとし、これを$\psi(q,t')$とします。このとき、任意の位置と時刻$q,t$における波動関数を
\begin{align} \psi(q,t)=\int dq' K(q,t; q',t')\psi(q',t') \end{align}
のように書くことにします。$K(q,t;q',t')$は状態$|q'\rangle$から$|q\rangle$への発展演算子です。

この発展演算子を直感的にわかりやすく記述する方法があります。それが経路積分です。時間を$N$等分し、微小時間幅$\epsilon$に対する時間発展演算子を$e^{-i\hat H(\hat q,\hat p)\epsilon}$とします。各時刻における$|q_k\rangle, |p_k\rangle \ \ (k=1,2,\cdots, n)$の完全系を挟んで計算すると以下を得ます：
\begin{align} K(q,t;q',t')=\langle q,t|q',t'\rangle=\lim_{N\to \infty} \int \cdots\int\prod_{i=1}^{N-1}dq(i)\prod_{j=0}^{N-1}\frac{dp(j)}{2\pi} \exp \left[ i\sum_{k=0}^{N-1}S[p(k),q(k+1),q(k)]/\hbar \right]\tag{1}\label{pathint0} \end{align}
なんだか小難しく感じますが、この表式は直感的理解を持ちます。

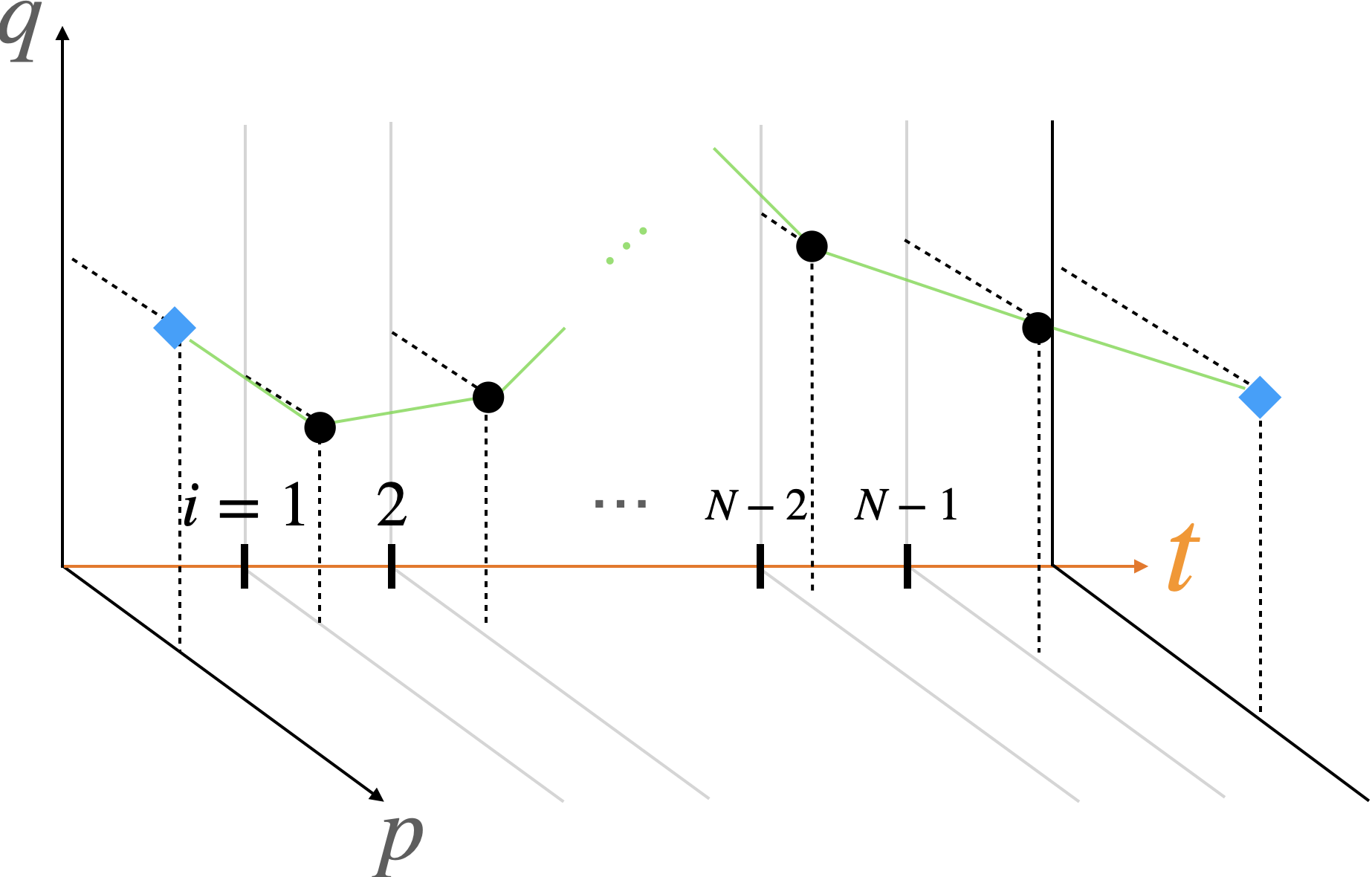経路積分の概念図

図1が式の概念図です。古典論において物体の運動は位置$q$と運動量$p$を各時刻で指定すれば定まります。時間を$N$分割し、$t=0$と$t=N$の$(q,p)$は定まっているとします（図の青い四角）。各時刻において様々な$(q,p)$を考え（図の黒い丸）、すべての可能な運動経路の集合の元に関して足し上げます。この各時刻における$(q,p)$の足し上げが、Eq.\eqref{pathint0}の各$i,j$での$(q,p)$の積分に対応します。これは「粒子の運動する経路の足し上げ」なので経路積分と呼ばれます。ただしその足し上げをするとき重みとしての位相をかける必要があります。その重みが式の$\exp$の部分です。これは$\exp(i\times \text{作用}/\hbar)$になります。

位相のファクターは、時間の各微小区間における時間発展演算子$\exp(-i\epsilon\hat H)$による部分、および運動量の固有状態と位置の固有状態の内積が$\langle q|p\rangle=\exp(iqp)$になることからもたらされる部分$p\dot q\simeq p(k)(q(k+1)-q(k))$から構成されています。

この表式は基本的には古典論からの延長にある量のみで構成されています。重みをかけて足すのも、統計的な操作だと思えば（位相は複素数なので確率解釈はできないのですが...）直感の範囲内だと思います。また、様々な経路の重ね合わせという概念は、量子力学では様々な状態を同時にとりうるという特徴とも整合的です。

$K$を簡潔に
\begin{align} K(q,t; q',t')&:=\langle q,t|q',t'\rangle =\int\cdots\int_{q(t')=q'}^{q(t)=q}{\cal D}q{\cal D}p \exp{iS[p,q]},\\ S[p,q]&:=\int_{t'}^t d\tau[p(\tau)\dot q(\tau)-H(p(\tau),q(\tau))] \end{align}
のように省略して書きます。$S$の被積分関数はラグランジアンです。
ここでHamiltonianを
\begin{align} H=\frac{1}{2}pW(q)p+V(q) \end{align}
とします。このとき運動量に関して積分することができて、
\begin{align} K(q,t_F;q',t_I)&=\lim_{N\to \infty} \int \cdots\int \prod^n_{i=1}\prod_{k=1}^{N-1} dq^i(k) \left( \frac{1}{2\pi i\epsilon} \right)^{nN/2} \exp(\frac{i}{\hbar}\sum_{k=0}^{N-1}A_k)\\ A_k&=\frac{1}{2\epsilon}(q(k+1)-q(k))M(q(k+1)-q(k))-\epsilon V(\bar q(k))-\frac{i}{2}{\rm tr}\ln M(\bar q(k))\tag{1}\label{pathint} \end{align}
を得ます。ここで$M:=W^{-1}$です。$A_k$の最後の項はLee-Yang項と呼ばれる項ですが、$M\neq 1$の場合のみに現れる項であり、ふつうは存在しません。最初の項$\frac{1}{2}\dot qM \dot q$は運動項であり（ふつうは$M=1$）、ポテンシャル項がマイナスで入っているので、$A_k$は作用$S$に等しいです。

最終的に、波動関数の経路積分表示を以下のように表します：
\begin{align} \psi_{{q}_0}({q},T)=\int {\cal D}{q}e^{iS_T/\hbar} \end{align}

${\cal D}{q}$はEq.\eqref{pathint}における$\exp$以外の部分を表します。作用$S$についている$T$の添字は終端の時刻が$T$であることを示しています。この振幅は$t=0$で${q}_0$、$t=T$で${q}$となる確率振幅（Feynman核）です。以下では通常の力学系を扱うため、Lee-Yang項は現れません。この場合、経路積分とは、重み$e^{iS_T}$つきのすべての可能な経路の足し合わせに相当します。

この$\psi_{q_0}(q,T)$はSchrödinger方程式を満たします。その証明は例えばRef.Feynman1965に載っています。

経路積分の計算は多くの場合シュレーディンガー方程式を解くより難しいです。しかし正準形式にはない直感的な理解のしやすさ、また今後見るような古典解と量子効果との関係性が明らかになることなど、メリットも多いです。近年の場の量子論・超弦理論の発展は、経路積分抜きには成し得なかったものが多いと思います。

WKB近似

次の力学系を考えます：
\begin{align} S_T=\int_0^TLdt, \ \ \ L=\frac{1}{2}\dot q^2-V(q) \end{align}

今この系の古典解は任意の$q$に対して求まっているものとします:
\begin{align} q_{\rm cl}(t) \ \ \ (q_{\rm cl}(0)=q_0, \ q_{\rm cl}(T)=q) \end{align}

Feynman核
\begin{align} \psi_{q_0}(q,T)=\int {\cal D}qe^{iS_T/\hbar} \end{align}
を$\hbar$で展開し、$\hbar^0$のオーダーまで考えます。$q$を
\begin{align} q=q_{\rm cl}+\sqrt{\hbar}\eta \end{align}
と展開します。時刻の両端では$\eta=0$とし、積分変数を${q}$から${\eta}$に変換すると
\begin{align} \psi_{q_0}(q,T)\simeq \exp\left\{i\frac{S_T^{\rm cl}}{\hbar}\right\} \int_{{\eta} (T)={\eta}(0)=0}{\cal D}{\eta} \exp\left[ i\int_0^T dt\left\{ \frac{1}{2}\dot{\eta}^2(t)-\frac{1}{2}{\eta}(t)V''(t){\eta}(t) \right\}\right]\\ \times \exp\left[ \frac{1}{\sqrt{\hbar}}\int_0^T\left(\dot {q}_{\rm cl} \dot {\eta} -\frac{\partial}{\partial {q}}V(t){\eta}\right) \right] \end{align}
を得ます。ここで$S_T^{\rm cl}:=S_T({q}^{\rm cl})$です。また
\begin{align} \frac{\partial}{\partial{q}}V(t):= \left[\frac{\partial V({q})}{\partial q_i}\right]_{{q}={q}^{\rm cl}(t)}, \ \ \ V''(t):=\left[\frac{\partial^2V({q})}{\partial q_i\partial q_j}\right]_{{q}={q}^{\rm cl}(t)} \end{align}
です。最後の$\exp$の肩は部分積分により
\begin{align} \int_0^T\left(\dot {q}_{\rm cl} \dot {\eta} -\frac{\partial}{\partial {q}}V(t){\eta}\right) =-\int_0^T\left(\ddot {q}_{\rm cl} +\frac{\partial}{\partial {q}}V(t)\right) {\eta} \end{align}
であり、運動方程式によりゼロになります。ゆえに
\begin{align} \psi_{{q}_0}({q},T)\simeq \exp\left\{i\frac{S_T^{\rm cl}}{\hbar}\right\} \int_{{\eta} (T)={\eta}(0)=0}{\cal D}{\eta} \exp\left[ i\int_0^T dt\left\{ \frac{1}{2}\dot{\eta}^2(t)-\frac{1}{2}{\eta}(t)V''(t){\eta}(t) \right\}\right] \end{align}
となります。

ここで虚時間に移ります。すなわち
\begin{align} \tau:=it \end{align}
として$\tau$で式を書き直します。これをEuclid化と言います。すると
\begin{align} i\int_0^T dt\left\{ \frac{1}{2}\dot{\eta}^2(t)-\frac{1}{2}{\eta}(t)V''(t){\eta}(t) \right\} \to -\int_0^\beta d\tau \left(\frac{1}{2}\dot\eta^2 +\frac{1}{2}\eta V''\eta\right) \end{align}
となります。ここで矢印の右側の量はすべて$\tau$の関数であり、また$\dot \eta$は虚時間$\tau$での微分を表します。積分の上限は$\beta$としました。以上から虚時間におけるFeynman核は以下のようになります：
\begin{align} \psi_{{q}_0}({q},\beta)\simeq \exp\left\{-\frac{S_\beta^{\rm cl}}{\hbar}\right\} \int_{{\eta} (\beta)={\eta}(0)=0}{\cal D}{\eta} \exp\left[ -\int_0^\beta d\tau\left\{ \frac{1}{2}\dot{\eta}^2(\tau)+\frac{1}{2}{\eta}(\tau)V''(\tau){\eta}(\tau) \right\}\right]\tag{2}\label{kernel} \end{align}
この表式では古典解もEuclid化された空間での解であることに注意してください。

$\eta$に関する経路積分を実行します。そこで以下の公式を使います：
\begin{align} \int dx_1 dx_2 \cdots dx_n \exp\left(-\frac{1}{2}{\boldsymbol x}^T M{\boldsymbol x}\right)\sim (\det M)^{-1/2}\tag{3}\label{formula} \end{align}
ここで$\boldsymbol x:=(x_1,x_2,\cdots,x_n)^T$、$M$は$n\times n$の行列です。ただし固有値はノンゼロとします。本来係数がつきますが、以降の議論ではそれは必要ないので省略しました。これを$\eta$の経路積分に適用するために時間を離散化し、$\boldsymbol\eta$を離散化された各虚時刻に関する$\eta(\tau)$のベクトル表示とし、また$\hat V''$を各虚時刻に依存する行列とします。すると
\begin{align} \int_0^\beta d\tau\left\{ \frac{1}{2}\dot\eta^2+\frac{1}{2}\eta V'' \eta \right\} &=\int_0^\beta d\tau\left\{ -\frac{1}{2}\eta\ddot \eta+\frac{1}{2}\eta V'' \eta\right\}\\ &\xrightarrow{\text{離散化}} -\frac{1}{2}{\boldsymbol\eta}^T\left(-\partial^2_\tau+\hat V'' \right) {\boldsymbol\eta} \end{align}
ここで$\partial_\tau^2$は虚時間における離散化された微分演算子であり、3重対角行列で表される差分演算子です。この表式をEq.\eqref{kernel}に代入し、Eq.\eqref{formula}を用いて計算すれば、以下の公式を得ます：

こうして、任意の終状態$q$に対して虚時間における古典解が求まれば、その周りの量子ゆらぎを${\cal O}(\hbar^0)$まで取り入れたFeynman核はEq.\eqref{final}で計算できることがわかります。

おしまい。${}_\blacksquare$

【次の記事】 インスタントンとトンネル効果 (2) : 二重井戸型ポテンシャルにおけるインスタントン